Studying-代码随想录训练营day29| 134. 加油站、135. 分发糖果、860.柠檬水找零、406.根据身高重建队列
第29天,贪心part03,快过半了(ง •_•)ง💪,编程语言:C++
目录
134.加油站
135. 分发糖果
860.柠檬水找零
406.根据身高重建队列
134.加油站
文档讲解:代码随想录加油站
视频讲解:手撕加油站
题目:
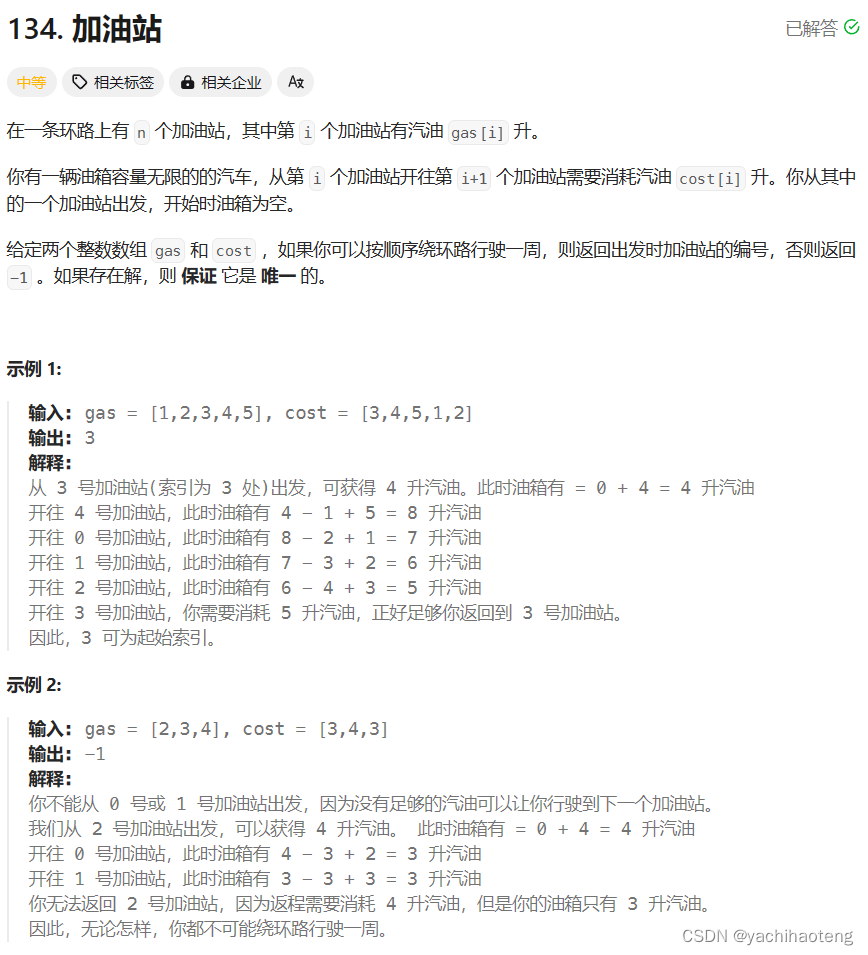
学习:本题其实很容易发现gas数组和cost数组的差,就是该站点结余的油量,我们在移动过程中理应让油量始终保持为正。因此本题的思考逻辑就是从某个站点出发,如果油量小于0则说明该点不能环路行驶一圈,反则则可以。
解法一:暴力解法,暴力遍历每个节点环行一周的结果。(力扣超时)
注意:for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,因此对于本题的场景需要使用while进行环行循环要十分注意。
//时间复杂度O(n^2)
//空间复杂度O(1)
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {for (int i = 0; i < cost.size(); i++) {int rest = gas[i] - cost[i]; // 记录剩余油量int index = (i + 1) % cost.size();while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了)rest += gas[index] - cost[index];index = (index + 1) % cost.size();}// 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置if (rest >= 0 && index == i) return i;}return -1;}
};解法二:贪心
贪心策略为:首先只有在总油量减去总消耗大于等于0的时候,才说明可以跑完一圈。其次我们在环行的过程中,还需要保持剩油量是正的,才能够继续行驶下去。因此我们可以 i 从0开始累加每个站点的剩油量(gas[i] - cost[i]),一旦累加和小于零,则说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油(一定不会说从中间开始某个点不会断油,因为如果是那样的话后半部分为正,那前半部分一定为负,也会使得满足剩油量为负的条件,跳到i+1),那么起始位置从i+1算起,再从0计算剩油量。
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
代码:
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {//贪心,局部最优找到累加为正的地方int count = 0; //计算总和,总和小于0说明无法环路一周int idcount = 0; //计算当前i往后的总和,该总和小于0说明不能从i出发int index = 0; //找到正确的出发下标for(int i = 0; i < gas.size(); i++) {int rest = gas[i] - cost[i];count += rest;idcount += rest;if(idcount < 0) { // 当前累加rest[i]和 curSum一旦小于0idcount = 0; // idcount从0开始计算index = i + 1; //起始位置更新为i+1}}if(count < 0) return -1;return index;}
};135. 分发糖果
文档讲解:代码随想录分发糖果
视频讲解:手撕分发糖果
题目:

学习:本题属于贪心算法中两个维度的问题,也就是需要两次贪心分别处理两种情况。本题中我们对于一个孩子来说,即要考虑他的左边和他的大小关系,又要考虑他的右边和他的大小关系,这就是我们要处理的两个问题。对于这种情况而言,我们需要将这两个问题分开解决,先考虑每个孩子右边比自身大的情况,再考虑每个孩子左边比自身大的情况,不能同时考虑,否则就会顾此失彼。
首先考虑右边孩子评分大的情况,从前向后遍历。此时的局部最优为:只要右边评分比左边大,右边的孩子就多一个糖果。全局最优为:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果。
接着我们再确定左边孩子评分大的情况,从后往前遍历。此时的局部最优就为:只要左边评分比右边大,左边的孩子就多一个糖果。全局最优为:相邻的孩子中,评分高的左孩子获得比右边孩子更多的糖果。(这个地方要注意,再更新评分更高的孩子的时候,我们要判断此时更新的值和原本的值谁更大,因为原本的值是保证了他和他左边孩子的关系,因为谁更大取谁,这样就能够同时保证左右孩子的关系了。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:int candy(vector<int>& ratings) {//两次贪心vector<int> candys(ratings.size(), 1); //初始化先给每个小孩一个糖果//第一次贪心,从左向右,先遍历右孩子比左孩子大的情况,局部最优:右孩子比左孩子大就多一个糖果for(int i = 1; i < ratings.size(); i++) {if(ratings[i] > ratings[i - 1]) {candys[i] = candys[i - 1] + 1;}}//第二次贪心,从右向左,遍历左孩子比右孩子大的情况,局部最优:左孩子比右孩子大就多一个糖果for(int i = ratings.size() - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {//这里要注意要去当前值和右孩子加1之间的最大值,这样才能保证该点同时大于左右孩子。candys[i] = max(candys[i], candys[i + 1] + 1); }}//求和int result = 0;for(int i = 0; i < candys.size(); i++) {result += candys[i];}return result;}
};860.柠檬水找零
文本讲解:代码随想录柠檬水找零
视频讲解:手撕柠檬水找零
题目:

学习:本题看起来题干很多很复杂,但实际上就是每位顾客花5美元买柠檬水,但这个过程中会出现三种情况分别是:1.顾客给了5美元,不需要找钱;2.顾客给了10美元,需要找5美元给顾客;3.顾客给了20美元,需要找15美元给顾客。针对这三种情况我们可以逐个分析。
1.顾客给了5美元:对于这种情况,我们不需要找钱的同时,我们手里还多了一张5美元。
2.顾客给了10美元,需要找5美元:对于这种情况,需要我们手头上有至少一张5美元,否则我们就不能正确找零返回false。如果我们手头上有至少一张5美元,则我们减少一张5美元,多一张10美元。
3.顾客给了20美元,需要找15美元:对于这种情况,就是需要我们进行贪心算法的时候了,因为对于我们来说5美元既可以给10美元的顾客找钱,又可以给20美元的顾客找钱。因此我们在给20美元的顾客找钱的时候应优先消耗美元10,保留更加万能的5美元,这样才能更好的进行正确的找零。因此有三种情况:1.手头上有10美元,5美元,则减少一张10美元,一张5美元;2.手头上美元10美元,但5美元大于3张,则减少3张5美元;3.手头上凑不出15美元的数(注意两张10美元不行)返回false。
代码:根据以上三种情况,则可编写代码
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:bool lemonadeChange(vector<int>& bills) {//记录手头上5美元和10美元的数量,20美元的不需要记录,因为20没有不能用于找钱int count5 = 0;int count10 = 0;for(int i = 0; i < bills.size(); i++) {//分别处理收到三种钱的情况if(bills[i] == 5) {count5++;}if(bills[i] == 10) {if(count5 == 0) {return false;}count5--;count10++;}//第三种情况需要进行贪心//贪心策略:如果有10元钞票优先找10元钞票,因为5元钞票比10元钞票更万能if(bills[i] == 20) {if(count10 > 0 && count5 > 0) {count10--;count5--;}else if(count5 >= 3) {count5 -= 3;}else {return false;}}}return true;}
};406.根据身高重建队列
文档讲解:代码随想录根据身高重建队列
视频讲解:手撕根据身高重建队列
题目:
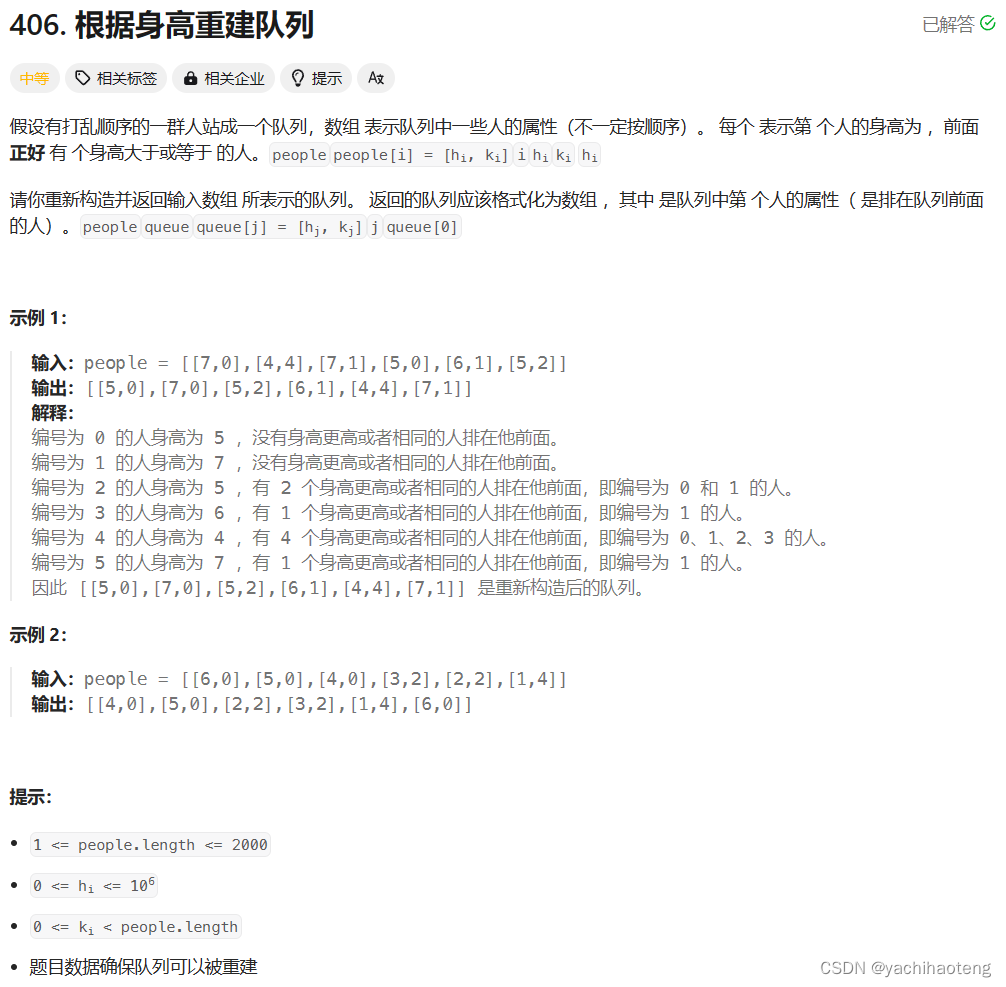
学习:本题与分发糖果相同,同样都是两维问题,我们需要分别考虑身高和前面身高大于等于的人的数量这两个因素。不能两个维度一起考虑,一定会出现顾此失彼的情况。
本题中如果我们需要对数组先进行排序,来解决一个维度上的问题。如果我们选择对k(身高大于等于的数量)进行排序,会发现最后得到的数组会发现k的排列不符合条件,身高也不符合条件,两个维度都没办法确定下来(这是因为会存在部分身高很高,因此k为0的干扰)。
因此本题我们需要先对身高进行排序,身高从高到低进行排序,这样也会有个好处,排序之后,如果后面的位置出现问题需要前插,也不会影响前面的数的排序,因为后面的数一定比前面的数小,不会影响到k值。
因此本题的贪心就是:局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性;全局最优:最后都做完插入操作,整个队列满足题目队列属性。
代码:
//时间复杂度O(nlogn + n^2)
//空间复杂度O(n)
class Solution {
public:static bool camp(vector<int>&a, vector<int>&b) {//身高从大到小排列,便于进行插入处理if(a[0] != b[0]) {return a[0] > b[0];}else { //如果身高一样,让其前面身高少的排前面return a[1] < b[1];}}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {//对数组进行排序,让身高高的先排前面,这样我们就能依据前面身高的数量,来插入每一个数sort(people.begin(), people.end(), camp);//贪心策略,遍历数组,优先按照身高高的people的k来进行插入,这样也就不用担心后续身高矮的插入造成影响vector<vector<int>> queue; //这里不能初始化数组的大小,因为后续要采用插入进行操作for(int i = 0; i < people.size(); i++) {int index = people[i][1]; //确定要插入的位置queue.insert(queue.begin() + people[i][1], people[i]);}return queue;}
};本题中存在一个问题,使用vector是非常费时的,C++中vector(可以理解是一个动态数组,底层是普通数组实现的)如果插入元素大于预先普通数组大小,vector底部会有一个扩容的操作,即申请两倍于原先普通数组的大小,然后把数据拷贝到另一个更大的数组上。所以使用vector(动态数组)来insert,是费时的,插入再拷贝的话,单纯一个插入的操作就是O(n^2)了,甚至可能拷贝好几次,就不止O(n^2)了。
代码:因此本题可以采用list类来保存数组,虽然时间复杂度没变,但实际效率是增加了的。
class Solution {
public:// 身高从大到小排(身高相同k小的站前面)static bool cmp(const vector<int>& a, const vector<int>& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0];}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort (people.begin(), people.end(), cmp);list<vector<int>> que; // list底层是链表实现,插入效率比vector高的多for (int i = 0; i < people.size(); i++) {int position = people[i][1]; // 插入到下标为position的位置std::list<vector<int>>::iterator it = que.begin();while (position--) { // 寻找在插入位置it++;}que.insert(it, people[i]);}return vector<vector<int>>(que.begin(), que.end());}
};相关文章:

Studying-代码随想录训练营day29| 134. 加油站、135. 分发糖果、860.柠檬水找零、406.根据身高重建队列
第29天,贪心part03,快过半了(ง •_•)ง💪,编程语言:C 目录 134.加油站 135. 分发糖果 860.柠檬水找零 406.根据身高重建队列 134.加油站 文档讲解:代码随想录加油站 视频讲解:手撕加油站…...

Understanding Zero Knowledge Proofs (ZKP)
Bilingual Tutorial: Understanding Zero Knowledge Proofs (ZKP) 双语教程:理解零知识证明(ZKP) Introduction 介绍 English: Zero Knowledge Proofs (ZKP) are a fascinating concept in cryptography where one party (the prover) can…...

微信小程序 DOM 问题
DOM 渲染问题 问题 Dom limit exceeded, please check if theres any mistake youve made.测试页面 1 <template><scroll-view scroll"screen" style"width: 100%;height: 100vh;" :scroll-y"true" :scroll-with-animation"tru…...

可视化作品集(03):旅游景区的应用,美爆啦。
景区可视化通常指的是利用现代科技手段,如地图、虚拟现实(VR)、增强现实(AR)、无人机航拍等技术,将景区的地理信息、景点分布、交通路线、游客服务设施等内容以可视化的方式呈现给游客或者管理者࿰…...

嵌入式实时操作系统:Intewell操作系统与VxWorks操作系统有啥区别
Intewell操作系统和VxWorks操作系统都是工业领域常用的操作系统,它们各有特点和优势。以下是它们之间的一些主要区别: 架构差异: Intewell操作系统采用微内核架构,这使得它具有高实时性、高安全性和强扩展性的特点。微内核架构…...
PCDN技术如何提高内容分发效率?(壹)
PCDN技术提高内容分发效率的操作主要体现在以下几个方面: 利用P2P技术:PCDN以P2P技术为基础,通过挖掘利用边缘网络的海量碎片化闲置资源,实现内容的分发。这种方式可以有效减轻中心服务器的压力,降低内容传输的延迟&a…...

Java 中Json中既有对象又有数组的参数 如何转化成对象
1.示例一:解析一个既包含对象又包含数组的JSON字符串,并将其转换为Java对象 在Java中处理JSON数据,尤其是当JSON结构中既包含对象又包含数组时,常用的库有org.json、Gson和Jackson。这里我将以Gson为例来展示如何解析一个既包含对…...
)
什么是数据挖掘(python)
文章目录 1.什么是数据挖掘2.为什么要做数据挖掘?3数据挖掘有什么用处?3.1分类问题3.2聚类问题3.3回归问题3.4关联问题 4.数据挖掘怎么做?4.1业务理解(Business Understanding)4.2数据理解(Data Understanding&#x…...

【Tomcat】Linux下安装帆软(fineReport)服务器 Tomcat
需求:帆软(fineReport)数据集上传至服务器 工具:XSHELL XFTP 帮助文档 一. 安装帆软服务器Tomcat 提供 Linux X86 和 Linux ARM 两种类型的部署包 ,所以在下载部署钱需要确认系统架构不支持在 32 位操作系统上安装 查…...

C++ | Leetcode C++题解之第213题打家劫舍II
题目: 题解: class Solution { public:int robRange(vector<int>& nums, int start, int end) {int first nums[start], second max(nums[start], nums[start 1]);for (int i start 2; i < end; i) {int temp second;second max(fi…...

windows系统中快速删除node_modules文件
npx命令方式 npx rimraf node_modules 项目中设置 "scripts": {# 安装依赖"i": "pnpm install",# 检测可更新依赖"npm:check": "npx npm-check-updates",# 删除 node_modules"clean": "npx rimraf node_m…...
返回值为void类型的页面跳转)
Spring MVC数据绑定和响应——页面跳转(一)返回值为void类型的页面跳转
一、返回值为void类型的页面跳转到默认页面 当Spring MVC方法的返回值为void类型,方法执行后会跳转到默认的页面。默认页面的路径由方法映射路径和视图解析器中的前缀、后缀拼接成,拼接格式为“前缀方法映射路径后缀”。如果Spring MVC的配置文件中没有配…...

CSS动画keyframes简单样例
一、代码部分 1.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><link rel"stylesheet" href…...
LabVIEW风机跑合监控系统
开发了一种基于LabVIEW的风机跑合监控系统,提高风机测试的效率和安全性。系统通过自动控制风机的启停、实时监控电流和功率数据,并具有过流保护功能,有效减少了人工操作和安全隐患,提升了工业设备测试的自动化和智能化水平。 项目…...

sql语句练习注意点
1、时间可以进行排序,也可以用聚合函数对时间求最大值max(时间) 例如下面的例子:取最晚入职的人,那就是将入职时间倒序排序,然后limit 1 表: 场景:查找最晚入职员工的所有信息 se…...

如视“VR+AI”实力闪耀2024世界人工智能大会
7月4日,2024世界人工智能大会暨人工智能全球治理高级别会议(以下简称为“WAIC 2024”)在上海盛大开幕,本届大会由外交部、国家发展和改革委员会、教育部等部门共同主办,围绕“以共商促共享 以善治促善智”主题…...

华为云交付模式和技术支持
华为云交付模式概览 用户由于自身或者企业属性的原因,对于使用云服务的要求也会有所不同。因此,华为云针对于不同用户的不同要求,提供了以下三种交付模式供用户选择。 公有云模式 公有云的核心属性是共享资源服务华为公有云为个人和企业用户…...

RK3568平台(opencv篇)ubuntu18.04上安装opencv环境
一.什么是 OpenCV-Python OpenCV-Python 是一个 Python 绑定库,旨在解决计算机视觉问题。 Python 是一种由 Guido van Rossum 开发的通用编程语言,它很快就变得非常流行,主要是 因为它的简单性和代码可读性。它使程序员能够用更少的代码行…...

R-CNN:深度学习在目标检测中的革命
R-CNN:深度学习在目标检测中的革命 目标检测是计算机视觉领域的一个核心问题,而R-CNN(Regions with Convolutional Neural Networks)算法是这一领域的一个重要里程碑。R-CNN及其后续的多种变体,如Fast R-CNN和Faster …...
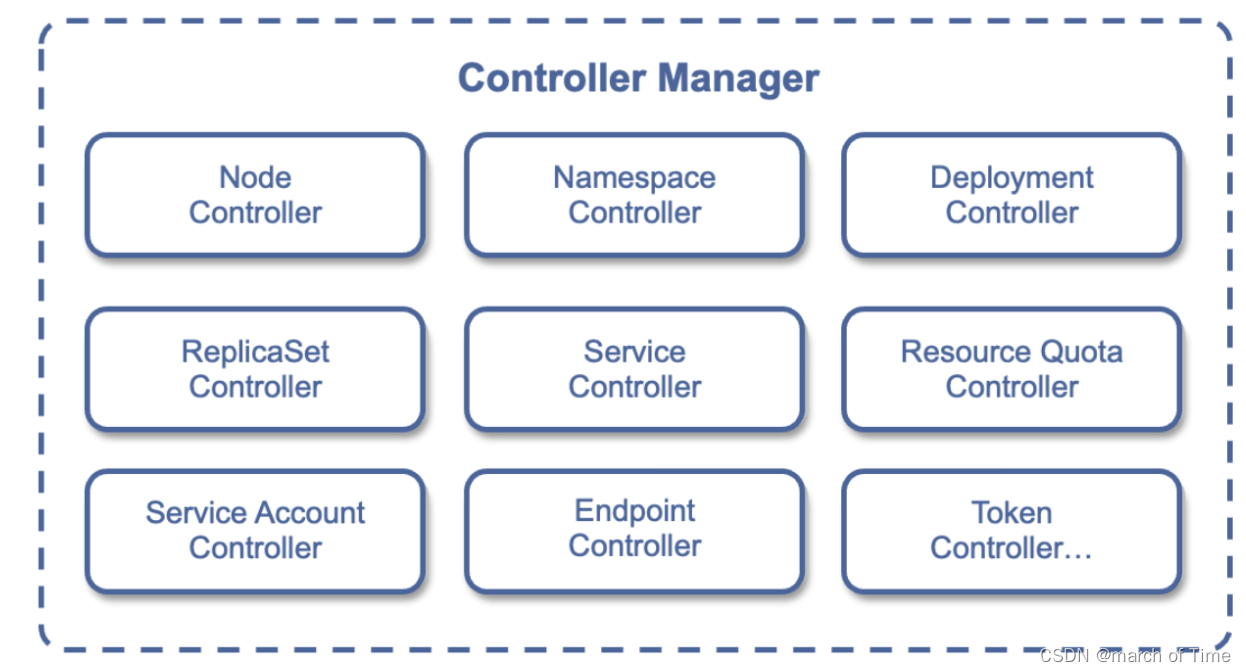
docker容器技术、k8s的原理和常见命令、用k8s部署应用步骤
容器技术 容器借鉴了集装箱的概念,集装箱解决了什么问题呢?无论形状各异的货物,都可以装入集装箱,集装箱与集装箱之间不会互相影响。由于集装箱是标准化的,就可以把集装箱整齐摆放起来,装在一艘大船把他们…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
