【2023ICPC网络赛I 】E. Magical Pair

当时在做洛谷U389682 最大公约数合并的时候我就想到把每个质因子分解出来然后跑高维前缀和,但是那一道题不是用这个方法,所有我也一直在思考这种做法是不是真的有用。因为昨天通过2024上海大学生程序设计竞赛I-六元组计数这道题我了解到了不少关于原根的性质,所以想着回来做去年网络赛的题目。因为我当时完全不了解原根,因此做不了这个题目,更看不懂题解,但是我现在已经大概掌握原根的知识,所以感觉做这道题还算比较轻松,而且这道题里面刚好就用到了曾经想到的质因数分解+高维前缀和,感觉十分有趣,于是写博客记录。
因为原根的题目一般都喜欢把0先处理掉,然后在处理不为0的情况。
很显然,如果想让左右两边为0,只需要满足 n ∣ x , n ∣ y n|x,n|y n∣x,n∣y,方案数为 ( n − 1 ) 2 (n-1)^2 (n−1)2。
然后我的想法是先列出一个 ( n − 1 ) ∗ ( n − 1 ) (n-1)*(n-1) (n−1)∗(n−1)的表, 1 < = x < = n − 1 , 1 < = y < = n − 1 , a i , j = i j 1<=x<=n-1,1<=y<=n-1,a_{i,j}=i^j 1<=x<=n−1,1<=y<=n−1,ai,j=ij。实际上,表上每一个位置都表示 n ∗ ( n − 1 ) n*(n-1) n∗(n−1)个数,因为实际上它的行坐标可以加上若干个 n n n,列坐标可以加上若干个 n − 1 n-1 n−1。然后就可以发现任意两个值相同的位置(可以一样)都恰好对应了一个解(我也不清楚如果以前没有看过题解能不能想到这一步)。比如两个坐标分别为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2),如果我们想形成一个解,那么就必须要让 x 1 + k 1 n = y 2 + k 2 ( n − 1 ) , y 1 + k 3 ( n − 1 ) = x 2 + k 4 n x_1+k_1n=y_2+k_2(n-1),y_1+k_3(n-1)=x_2+k_4n x1+k1n=y2+k2(n−1),y1+k3(n−1)=x2+k4n,这个根据扩展欧几里得可以知道如果想找到另外一个解,那么 k 1 , k 4 k_1,k_4 k1,k4都必须改变 n − 1 n-1 n−1, k 2 , k 3 k_2,k_3 k2,k3都必须改变 n n n,因此两个相同值的位置恰好对应一个解。
因此,我们就必须算出每个数出现的次数,答案就是这个出现次数的平方和。
根据原根的性质,和 n − 1 n-1 n−1最大公因数相同的数出现次数一样, 然后我们就把和 n − 1 n-1 n−1最大公因数相同的数全部在一个组,然后考虑组合组之间的影响(详见2024上海大学生程序设计竞赛I-六元组计数&原根知识详解。
我们就考虑每个集合的最小的数,那么只有它的因子所在的集合会出现这个数,实际上就是一个周期出现一次, g c d ( x , n − 1 ) = y gcd(x,n-1)=y gcd(x,n−1)=y的数有 y y y个周期,所以贡献就是。
( n − 1 ) 2 + ∑ i ∣ n − 1 ϕ ( n − 1 i ) ( ∑ j ∣ i ϕ ( n − 1 j ) j ) 2 (n-1)^2+\sum_{i|n-1}\phi(\frac{n-1}{i})(\sum_{j|i}\phi(\frac{n-1}{j})j)^2 (n−1)2+∑i∣n−1ϕ(in−1)(∑j∣iϕ(jn−1)j)2
我们可以预处理出 2 ∗ 1 0 7 2*10^7 2∗107以内的质数(实测表明n-1的所有素因子都不会超过4*10^14,所有我只用处理出这么多),然后分解完质因数就用高位前缀和把 ∑ j ∣ i ϕ ( n − 1 j ) j \sum_{j|i}\phi(\frac{n-1}{j})j ∑j∣iϕ(jn−1)j计算出来即可。
#include<bits/stdc++.h>
#define rep(i,x,y) for(int i=x;i<=y;i++)
#define dwn(i,x,y) for(int i=x;i>=y;i--)
#define ll long long
using namespace std;
template<typename T>inline void qr(T &x){x=0;int f=0;char s=getchar();while(!isdigit(s))f|=s=='-',s=getchar();while(isdigit(s))x=x*10+s-48,s=getchar();x=f?-x:x;
}
int cc=0,buf[31];
template<typename T>inline void qw(T x){if(x<0)putchar('-'),x=-x;do{buf[++cc]=int(x%10);x/=10;}while(x);while(cc)putchar(buf[cc--]+'0');
}
const int N=2e7+10,M=2e5+10,mod=998244353;
int cnt;ll p[N];bool v[N];
ll n,ans;
struct node{ll x,y;
}a[210];int m;ll val[210];
ll phi[M],lim,dp[M],num[M];
void solve(){qr(n);if(n==2){puts("2");return;}n--;ll nn=n;ans=(n%mod)*(n%mod)%mod;m=0;rep(i,1,cnt){if(p[i]*p[i]>n)break;if(n%p[i]==0){a[++m].x=p[i];a[m].y=0;while(n%p[i]==0)a[m].y++,n/=p[i];}}if(n>1)a[++m]=(node){n,1};val[1]=1;rep(i,2,m)val[i]=val[i-1]*(a[i-1].y+1);lim=val[m]*(a[m].y+1);rep(i,0,lim-1){if(!i){phi[i]=1;num[i]=1;continue;}bool bk=0;rep(j,1,m){ll t=i/val[j]%(a[j].y+1);if(t){if(t==1)phi[i]=phi[i-val[j]]*(a[j].x-1);else phi[i]=phi[i-val[j]]*a[j].x;num[i]=num[i-val[j]]*a[j].x;break;}}}rep(i,0,lim-1)dp[i]=(phi[lim-1-i]%mod)*(num[i]%mod)%mod;rep(i,1,m)rep(j,val[i],lim-1)if(j/val[i]%(a[i].y+1))(dp[j]+=dp[j-val[i]])%=mod;rep(i,0,lim-1){dp[i]=dp[i]*dp[i]%mod;(ans+=(phi[lim-1-i]%mod)*dp[i]%mod)%=mod;}cout<<ans<<endl;
}
int main(){rep(i,2,20000000){if(!v[i])v[i]=1,p[++cnt]=i;for(int j=1;j<=cnt&&i*p[j]<=20000000ll;j++){v[i*p[j]]=1;if(i%p[j]==0)break;}}int tt;qr(tt);while(tt--)solve();return 0;
}相关文章:

【2023ICPC网络赛I 】E. Magical Pair
当时在做洛谷U389682 最大公约数合并的时候我就想到把每个质因子分解出来然后跑高维前缀和,但是那一道题不是用这个方法,所有我也一直在思考这种做法是不是真的有用。因为昨天通过2024上海大学生程序设计竞赛I-六元组计数这道题我了解到了不少关于原根的…...
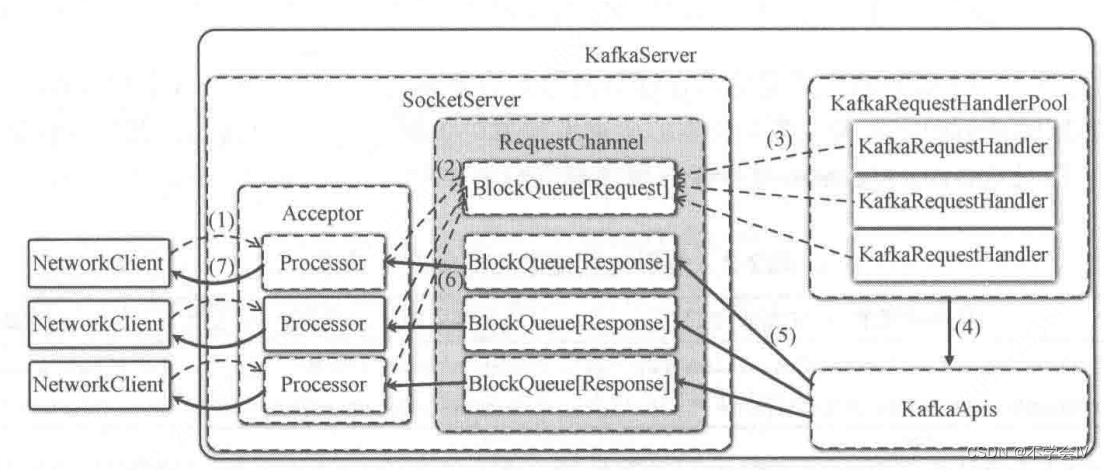
Kafka-服务端-网络层-源码流程
整体架构如下所示: responseQueue不在RequestChannel中,在Processor中,每个Processor内部有一个responseQueue 客户端发送的请求被Acceptor转发给Processor处理处理器将请求放到RequestChannel的requestQueue中KafkaRequestHandler取出reque…...

百日筑基第十一天-看看SpringBoot
百日筑基第十一天-看看SpringBoot 创建项目 Spring 官方提供了 Spring Initializr 的方式来创建 Spring Boot 项目。网址如下: https://start.spring.io/ 打开后的界面如下: 可以将 Spring Initializr 看作是 Spring Boot 项目的初始化向导ÿ…...

Generative Modeling by Estimating Gradients of the Data Distribution
Generative Modeling by Estimating Gradients of the Data Distribution 本文介绍宋飏提出的带噪声扰动的基于得分的生成模型。首先介绍基本的基于得分的生成模型的训练方法(得分匹配)和采样方法(朗之万动力学)。然后基于流形假…...

vector与list的简单介绍
1. 标准库中的vector类的介绍: vector是表示大小可以变化的数组的序列容器。 就像数组一样,vector对其元素使用连续的存储位置,这意味着也可以使用指向其元素的常规指针上的偏移量来访问其元素,并且与数组中的元素一样高效。但与数…...

四种线程池的使用,优缺点分析
池化思想:线程池、字符串常量池、数据库连接池 提高资源的利用率 下面是手动创建线程和执行任务过程,可见挺麻烦的,而且线程利用率不高。 手动创建线程对象执行任务执行完毕,释放线程对象 线程池的优点: 提高线程的…...

什么是 BEM 规范
BEM(Block, Element, Modifier)是一种 CSS 命名规范,旨在提高代码的可读性和可维护性。BEM 规范通过明确的命名规则来定义组件和组件的各个部分,使开发者能够更容易地理解和维护代码。 BEM 命名规范的基本概念 Block(…...

【Node.JS】入门
文章目录 Node.js的入门涉及对其基本概念、特点、安装、以及基本使用方法的了解。以下是对Node.js入门的详细介绍: 一、Node.js基本概念和特点 定义:Node.js是一个基于Chrome V8引擎的JavaScript运行环境,它使得JavaScript能够运行在服务器…...

Amazon SageMaker 机器学习之旅的助推器
一、前言 在当今的数字化时代,人工智能和机器学习已经成为推动社会进步的重要引擎。亚马逊云科技在 2023 re:Invent 全球大会上,宣布推出五项 Amazon SageMaker 新功能: Amazon SageMaker HyperPod 通过为大规模分布式训练提供专用的基础架构…...

TransMIL:基于Transformer的多实例学习
MIL是弱监督分类问题的有力工具。然而,目前的MIL方法通常基于iid假设,忽略了不同实例之间的相关性。为了解决这个问题,作者提出了一个新的框架,称为相关性MIL,并提供了收敛性的证明。基于此框架,还设计了一…...

3.用户程序与驱动交互
驱动程序请使用第二章https://blog.csdn.net/chenhequanlalala/article/details/140034424 用户app与驱动交互最常见的做法是insmod驱动后,生成一个设备节点,app通过open,read等系统调用去操作这个设备节点,这里先用mknode命令调…...
尽量不写一行if...elseif...写出高质量可持续迭代的项目代码
背景 无论是前端代码还是后端代码,都存在着定位困难,不好抽离,改造困难的问题,造成代码开发越来越慢,此外因为代码耦合较高,总是出现改了一处地方,然后影响其他地方,要么就是要修改…...

xcrun: error: unable to find utility “simctl“, not a developer tool or in PATH
目录 前言 一、问题详情 二、解决方案 1.确认Xcode已安装 2.安装Xcode命令行工具 3.指定正确的开发者目录 4. 确认命令行工具路径 5. 更新PATH环境变量 前言 今天使用cocoapods更新私有库的时候,遇到了"xcrun: error: unable to find utility &…...

【linux高级IO(一)】理解五种IO模型
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux高级IO 1. 前言2. 重谈对…...

前端引用vue/element/echarts资源等引用方法Blob下载HTML
前端引用下载vue/element/echarts资源等引用方法 功能需求 需求是在HTML页面中集成Vue.js、Element Plus(Element UI的Vue 3版本)、ECharts等前端资源,使用Blob下载HTML。 解决方案概述 直接访问线上CDN地址:简单直接,…...

昇思MindSpore学习笔记2-01 LLM原理和实践 --基于 MindSpore 实现 BERT 对话情绪识别
摘要: 通过识别BERT对话情绪状态的实例,展现在昇思MindSpore AI框架中大语言模型的原理和实际使用方法、步骤。 一、环境配置 %%capture captured_output # 实验环境已经预装了mindspore2.2.14,如需更换mindspore版本,可更改下…...

uniapp实现图片懒加载 封装组件
想要的效果就是窗口滑动到哪里,哪里的图片进行展示 主要原理使用IntersectionObserver <template><view><image error"HandlerError" :style"imgStyle" :src"imageSrc" :id"randomId" :mode"mode&quo…...

持续交付:自动化测试与发布流程的变革
目录 前言1. 持续交付的概念1.1 持续交付的定义1.2 持续交付的核心原则 2. 持续交付的优势2.1 提高交付速度2.2 提高软件质量2.3 降低发布风险2.4 提高团队协作 3. 实施持续交付的步骤3.1 构建自动化测试体系3.1.1 单元测试3.1.2 集成测试3.1.3 功能测试3.1.4 性能测试 3.2 构建…...

VBA常用的字符串内置函数
前言 在VBA程序中,常用的内置函数可以按照功能分为字符串函数、数字函数、转换函数等等,本节主要会介绍常用的字符串的内置函数,包括Len()、Left()、Mid()、Right()、Split()、String()、StrConV()等。 本节的练习数据表以下表为例ÿ…...
)
大数据面试题之Spark(7)
目录 Spark实现wordcount Spark Streaming怎么实现数据持久化保存? Spark SQL读取文件,内存不够使用,如何处理? Spark的lazy体现在哪里? Spark中的并行度等于什么 Spark运行时并行度的设署 Spark SQL的数据倾斜 Spark的exactly-once Spark的…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
