LeetCode 196, 73, 105
目录
- 196. 删除重复的电子邮箱
- 题目链接
- 表
- 要求
- 知识点
- 思路
- 代码
- 73. 矩阵置零
- 题目链接
- 标签
- 简单版
- 思路
- 代码
- 优化版
- 思路
- 代码
- 105. 从前序与中序遍历序列构造二叉树
- 题目链接
- 标签
- 思路
- 代码
196. 删除重复的电子邮箱
题目链接
196. 删除重复的电子邮箱
表
- 表
Person的字段为id和email。
要求
编写解决方案 删除 所有重复的电子邮件,只保留一个具有最小 id 的唯一电子邮件。
(对于 SQL 用户,请注意你应该编写一个 DELETE 语句而不是 SELECT 语句。)
(对于 Pandas 用户,请注意你应该直接修改 Person 表。)
运行脚本后,显示的答案是 Person 表。驱动程序将首先编译并运行您的代码片段,然后再显示 Person 表。Person 表的最终顺序 无关紧要 。
知识点
delete:删除数据。形式上类似于select。
思路
保留一个具有最小 id 的唯一电子邮件意味着删除所有 比最小 id 的电子邮件的 id 大 且 与其 email 相同 的电子邮件,所以可以使用多表“查询”,首先得限制两个表的 email 相同,然后删除 id 大的那些数据即可。
代码
deletep_big
fromPerson p_big,Person p_small
wherep_big.email = p_small.email
andp_big.id > p_small.id
73. 矩阵置零
题目链接
73. 矩阵置零
标签
数组 哈希表 矩阵
简单版
思路
如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。这意味着只需要用两个数组,分别存储这行和这列是否有0,如果这行有0,则将这行元素置零;如果这列有0,则将这列元素置零。
代码
class Solution {public void setZeroes(int[][] matrix) {int m = matrix.length, n = matrix[0].length;boolean[] isRow0 = new boolean[m];boolean[] isCol0 = new boolean[n];// 检查每一行和每一列是否有为0的数字for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == 0) {isRow0[i] = true;isCol0[j] = true;}}}// 置零for (int i = 0; i < m; i++) {if (isRow0[i]) {for (int j = 0; j < n; j++) {matrix[i][j] = 0;}}}for (int j = 0; j < n; j++) {if (isCol0[j]) {for (int i = 0; i < m; i++) {matrix[i][j] = 0;}}}}
}
优化版
思路
可以将统计每行每列是否有0的数组放到原矩阵中,这里使用每行的第一个元素(列首)和每列的第一个元素(行首)来统计当前行是否有0和当前列是否有0,如果有0,则列首或行首置为0。然后对“整个”(从第二行到最后一行,从第二列到最后一列的)矩阵进行扫描,如果这行第一个元素或这列第一个元素是0,则将该元素置零。
那么问题就来了,既然在此处修改了第一行和第一列,那么该如何判断原始的第一行和第一列是否需要置零呢?使用两个变量提前对第一行和第一列进行判断即可。在 对“整个”(从第二行到最后一行,从第二列到最后一列的)矩阵进行扫描 完毕后,对第一行和第一列进行操作,如果原先第一行有0,则将第一行置零;如果原先第一列有0,则将第一列置零。
注意:这样做不会破坏原矩阵(或者说不影响结果),因为如果某行(或某列)有0,那么这行(或这列)的所有元素都需要被置零。
代码
class Solution {public void setZeroes(int[][] matrix) {int m = matrix.length, n = matrix[0].length;boolean isFirstRow0 = false, isFirstCol0 = false;// 检查第一列是否有为0的数字for (int i = 0; i < m; i++) {if (matrix[i][0] == 0) {isFirstCol0 = true;break;}}// 检查第一行是否有为0的数字for (int i = 0; i < n; i++) {if (matrix[0][i] == 0) {isFirstRow0 = true;break;}}// 检查 第二行到最后一行 第二列到最后一列 是否有为0的数字for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (matrix[i][j] == 0) { // 如果有重复数字matrix[i][0] = matrix[0][j] = 0; // 则将本矩阵的 行首 和 列首 记为0}}}// 将 第二行到最后一行 第二列到最后一列 的元素置零for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (matrix[i][0] == 0 || matrix[0][j] == 0) { // 如果 本行首 或 本列首 被置零matrix[i][j] = 0; // 则将该元素置为0}}}// 如果原先矩阵的第一行有0,则将第一行置零if (isFirstRow0) {for (int j = 0; j < n; j++) {matrix[0][j] = 0;}}// 如果原先矩阵的第一列有0,则将第一行置零if (isFirstCol0) {for (int i = 0; i < m; i++) {matrix[i][0] = 0;}}}
}
105. 从前序与中序遍历序列构造二叉树
题目链接
105. 从前序与中序遍历序列构造二叉树
标签
树 数组 哈希表 分治 二叉树
思路
注意:如果遍历的结果中有相同的元素,则无法构造二叉树,所以本题中的遍历结果都是无重复值的。
先来思考一下只有中序遍历应该如何构造二叉树?众所周知,中序遍历是先遍历左子树、再处理本节点、最后遍历右子树,所以说在中序遍历的结果中,中间元素是父节点(前提是它左子树的节点数等于右子树的节点数),中间元素的左子区间为它的左子树,中间元素的右子区间为它的右子树。
根据中间节点把整个遍历结果拆分为两个子区间,这两个子区间也有这样的性质:子区间的中间元素是父节点(前提是它左子树的节点数等于右子树的节点数),中间元素的左子区间为它的左子树,右子区间为它的右子树。
例如底下的二叉树,它的中序遍历结果为[1, 2, 3, 4, 5, 6, 7],第一个父节点(根节点)为4,然后分出[1, 2, 3]和[5, 6, 7]这两个子区间。在[1, 2, 3]中找到父节点2,在[5, 6, 7]中找到父节点6,接着将区间分为长度为1的子区间。此时直接将这个值作为叶子节点(没有子节点的节点)即可。

既然只需要知道中序遍历就能够构造二叉树,那为什么还要前序遍历的结果?这是因为存在一种二叉树,这种二叉树有些节点只有一个子节点,就不能确定哪个节点是父节点。
比如底下的二叉树,它的中序遍历结果为[2, 3, 4, 5, 6, 7],此时就不能轻易地将4作为第一个父节点了,因为4的左右子树的节点数不相等。所以只知道中序遍历的结果是无法构造二叉树的,因为无法确定父节点。

在前序遍历的结果[4, 2, 3, 6, 5, 7]中,第一个元素4就是第一个父节点,然后在中序遍历的结果[2, 3, 4, 5, 6, 7]中寻找父节点,并划分左子树[2, 3]和右子树[5, 6, 7]。
发现左子树含有的元素[2, 3] 和 前序遍历结果[4, 2, 3, 6, 5, 7]去掉父节点4后截取前2个元素(2是左子树的长度)的结果[2, 3]含有的元素 恰好相同,右子树含有的元素[5, 6, 7] 和 前序遍历结果[4, 2, 3, 6, 5, 7]去掉父节点4后截取后3个元素(3是右子树的长度)的结果[6, 5, 7]含有的元素 恰好相同。
所以构造二叉树的策略就确定了:将前序遍历区间内第一个值作为二叉树的父节点,在中序遍历的结果中寻找这个值,然后将这个值左边的区间定义为左子树,右边的区间定义为右子树,接着将前序遍历的结果也进行划分,去除第一个元素后,将前n(n是中序遍历划分的左子树的长度)个元素作为左子树,将后m(m是中序遍历划分的右子树的长度)个元素作为右子树。划分完这两个数组后,分别构造左子树和右子树。
代码
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {if (preorder.length == 0) { // 如果preorder的长度为0return null; // 则退出递归}int parentValue = preorder[0]; // 记录父节点的值TreeNode parent = new TreeNode(parentValue); // 以preorder的第一个值作为父节点for (int i = 0; i < preorder.length; i++) {if (inorder[i] == parentValue) { // 如果在inorder中找到父节点int[] preLeft = Arrays.copyOfRange(preorder, 1, i + 1); // 截取preorder的左子树区间int[] preRight = Arrays.copyOfRange(preorder, i + 1, inorder.length); // 截取preorder的右子树区间int[] inLeft = Arrays.copyOfRange(inorder, 0, i); // 截取inorder的左子树区间int[] inRight = Arrays.copyOfRange(inorder, i + 1, inorder.length); // 截取inorder的右子树区间parent.left = buildTree(preLeft, inLeft); // 构造左子树parent.right = buildTree(preRight, inRight); // 构造右子树break;}}return parent; // 返回本轮递归的父节点}
}
相关文章:

LeetCode 196, 73, 105
目录 196. 删除重复的电子邮箱题目链接表要求知识点思路代码 73. 矩阵置零题目链接标签简单版思路代码 优化版思路代码 105. 从前序与中序遍历序列构造二叉树题目链接标签思路代码 196. 删除重复的电子邮箱 题目链接 196. 删除重复的电子邮箱 表 表Person的字段为id和email…...

在Apache HTTP服务器上配置 TLS加密
安装mod_ssl软件包 [rootlocalhost conf.d]# dnf install mod_ssl -y此时查看监听端口多了一个443端口 自己构造证书 [rootlocalhost conf.d]# cd /etc/pki/tls/certs/ [rootlocalhost certs]# openssl genrsa > jiami.key [rootlocalhost certs]# openssl req -utf8 -n…...

C语言力扣刷题11——打家劫舍1——[线性动态规划]
力扣刷题11——打家劫舍1和2——[线性动态规划] 一、博客声明二、题目描述三、解题思路1、线性动态规划 a、什么是动态规划 2、思路说明 四、解题代码(附注释) 一、博客声明 找工作逃不过刷题,为了更好的督促自己学习以及理解力扣大佬们的解…...
房屋租赁管理小程序的设计
管理员账户功能包括:系统首页,个人中心,用户管理,中介管理,房屋信息管理,房屋类型管理,租房订单管理,租房信息管理 微信端账号功能包括:系统首页,房屋信息&am…...

oracle sql语句 排序 fjd = ‘0101‘ 排在 fjd = ‘0103‘ 的前面
要实现这个排序需求,你可以使用 CASE 表达式来自定义排序逻辑。假设你有一个表格名为 your_table,并且有一个字段 fjd 存储类似 ‘0101’, ‘0103’ 这样的值,你可以这样编写 SQL 查询: SELECT * FROM your_table ORDER BY CASE …...
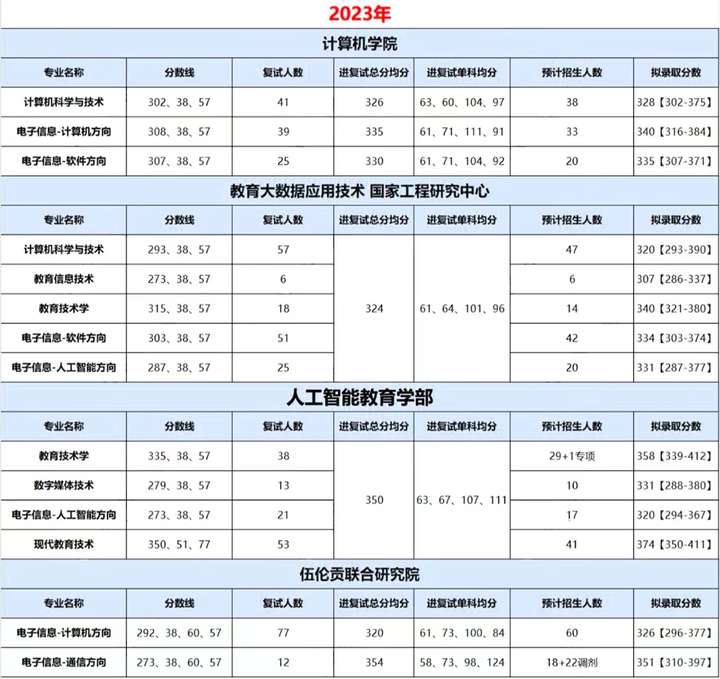
初试成绩占比百分之70!计算机专硕均分340+!华中师范大学计算机考研考情分析!
华中师范大学(Central China Normal University)简称“华中师大”或“华大”,位于湖北省会武汉,是中华人民共和国教育部直属重点综合性师范大学,国家“211工程”、“985工程优势学科创新平台”重点建设院校,…...

【面向就业的Linux基础】从入门到熟练,探索Linux的秘密(十)-git(2)
下面是一些git的常用命令和基本操作,可以当做平常的笔记查询,用于学习!!! 文章目录 前言 一、git 二、git常用命令 总结 前言 下面是一些git的常用命令和基本操作,可以当做平常的笔记查询,用于…...

JMH320【亲测】【御剑九歌】唯美仙侠手游御剑九歌+WIN学习手工端+视频教程+开服清档+运营后台+授权GM物品充值后台
资源介绍: 这也是仙梦奇缘的一个游戏 注意:外网14位IP或域名 ———————————————————————————————————– ps后台介绍: 1区运营后台:http://ip:9981/admin/admintool/ 2区运营后台:http://ip…...

【matlab】信号分解/故障诊断——智能优化算法优化VMD
目录 引言 应用领域 VMD代码实现 智能优化算法优化VMD 引言 VMD(变分模态分解)是一种新的非线性自适应信号分解方法,它通过变分原理将复杂信号分解为若干个具有不同频率中心和带宽的本征模态函数(Intrinsic Mode Functions, …...

【重磅】万能模型-直接能换迪丽热巴的模型
万能模型,顾名思义,不用重新训练src,直接可以用的模型,适应大部分原视频脸 模型用法和正常模型一样,但可以跳过训练阶段!直接到合成阶段使用该模型 本模型没有做Xseg,对遮挡过多的画面不会自动适…...

Web基础和HTTP协议
web基础与HTTP协议: web:就是我们所说的网页。打开网站展示的页面。(全球广域网,万维网) world wide web 分布式图形信息系统 http https 超文本传输协议 分布式:计算机系统或者应用程序分布在多台计算机或者服务器上。通过计算机网络互相通信和协作。共同完成任…...

Mini-L-CTF-2022 minispringboot Thymeleaf模板注入 spel的绕过
Mini-L-CTF-2022 minispringboot Thymeleaf模板注入 spel的绕过 就是一个低版本的Thymeleaf注入 漏洞点 public class MainController {GetMapping({"/{language}"})public String test(PathVariable(name "language") String language, RequestParam(…...

LLM - 神经网络的组成
1. 一个神经元的结构:即接受多个输入X向量,在一个权重向量W和一个偏执标量b的作用下,经过激活函数后,产生一个输出。 2. 一层神经网络的结构:该层网络里的每个神经元并行计算,得到各自的输出;计算方式是输入…...
C++:拷贝构造函数
拷贝构造函数的引入 用对象来初始化对象 (1)简单变量定义时,可以直接初始化,也可以用另一个同类型变量来初始化。举例说明 (2)用class来定义对象时,可以直接初始化,也可以用另一个对象来初始化。举例说明 testperson xiaohong(na…...

云服务出现故障这样处理
无法连接云服务器 服务器远程无法连接时,可通过7ECloud控制台进行连接。 常见故障现象 1、ping不通 2、ping丢包 3、部分端口telnet不通 4、全部端口telnet不通 5、广告、弹窗植入 6、域名无法访问IP访问正常 常见故障原因 1、云服务器过期、关机或者EIP被…...

CVPR2024自动驾驶轨迹预测方向的论文整理
2024年自动驾驶轨迹预测方向的论文汇总 1、Producing and Leveraging Online Map Uncertainty in Trajectory Prediction 论文地址:https://arxiv.org/pdf/2403.16439 提出针对在线地图不确定性带给轨迹预测的影响对应的解决方案。 在轨迹预测中,利用在…...
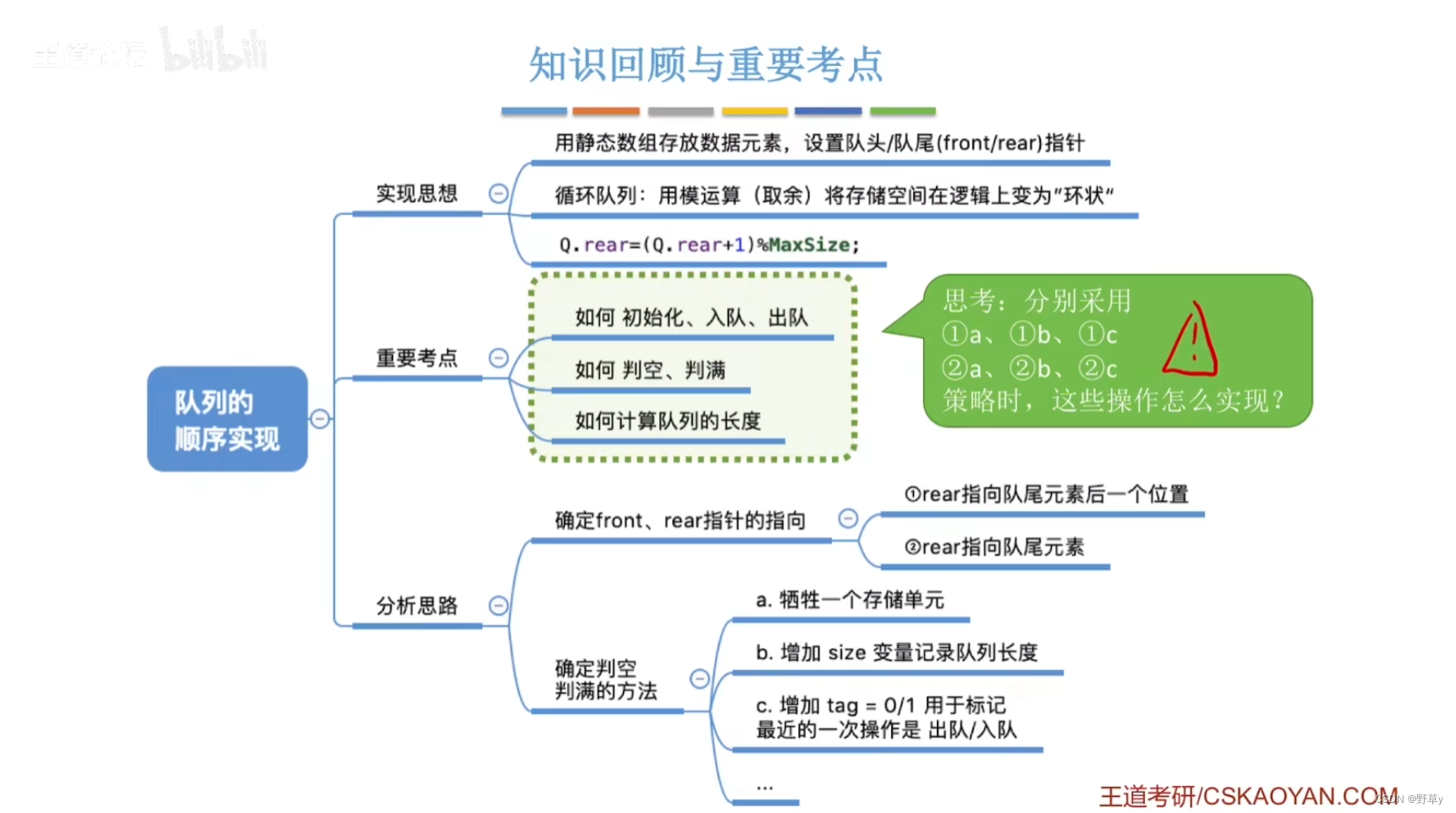
数据结构——队列练习题
在C语言中,.和->运算符用于访问结构体的成员变量。它们之间的区别在于:.运算符用于访问结构体变量的成员。->运算符用于访问结构体指针变量的成员 1a(rear指向队尾元素后一位,判空判满时牺牲一个存储单元) 首先…...

PLL和CDR的内部结构及其区别
比较PLL和CDR的内部结构及其区别: 基本结构: PLL(相位锁定环): 相位检测器环路滤波器压控振荡器(VCO)分频器(可选,用于频率合成) CDR(时钟数据恢复…...
HarmonyOS APP应用开发项目- MCA助手(Day02持续更新中~)
简言: gitee地址:https://gitee.com/whltaoin_admin/money-controller-app.git端云一体化开发在线文档:https://developer.huawei.com/consumer/cn/doc/harmonyos-guides-V5/agc-harmonyos-clouddev-view-0000001700053733-V5注:…...

华为交换机 LACP协议
华为交换机支持的LACP协议,即链路聚合控制协议,是一种基于IEEE 802.3ad标准的动态链路聚合与解聚合的协议。它允许设备根据自身配置自动形成聚合链路并启动聚合链路收发数据。 在LACP模式下,链路聚合组能够自动调整链路聚合,维护…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...
