MATLAB | 如何解决实验数据散点图重叠问题(overlap)

本期部分实验效果：

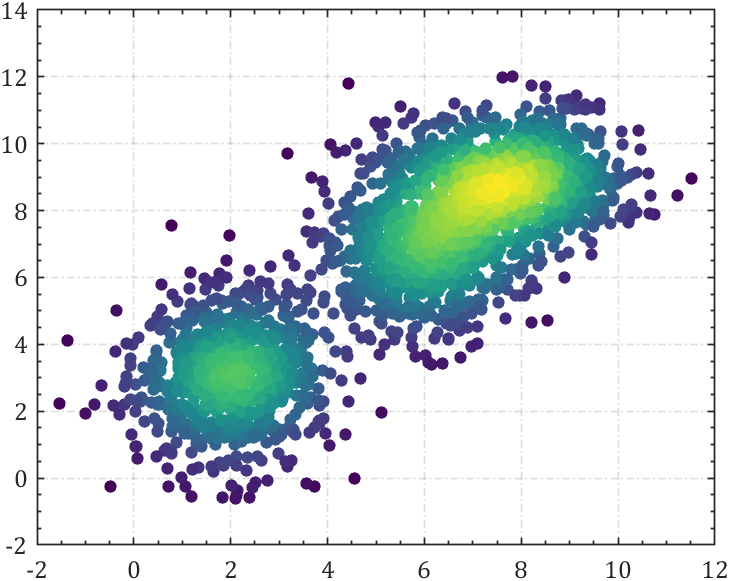
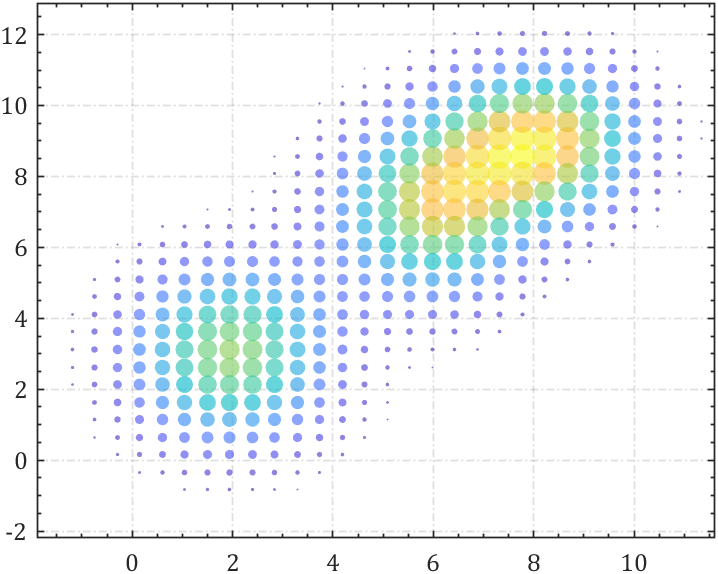
这期讲一下如果数据重合严重该咋办(overlap)，事先说明，本文中的绘图均使用一个几行的简单小代码进行了修饰：

function defualtAxes
ax=gca;hold on;box on
ax.XGrid='on';
ax.YGrid='on';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.LineWidth=.8;
ax.GridLineStyle='-.';
ax.FontName='Cambria';
ax.FontSize=12;
end

0 数据说明及基础绘图

假设我们随机构建两列数据：

% 随便生成散点
PntSet1=mvnrnd([2 3],[1 0;0 2],800);
PntSet2=mvnrnd([6 7],[1 0;0 2],800);
PntSet3=mvnrnd([8 9],[1 0;0 1],800);
PntSet=[PntSet1;PntSet2;PntSet3];
X=PntSet(:,1);
Y=PntSet(:,2);

scatter函数绘图效果：

% 使用scatter绘图
scatter(X,Y,'filled','CData',[36,59,66]./255);% 简单修饰，可省略
defualtAxes()

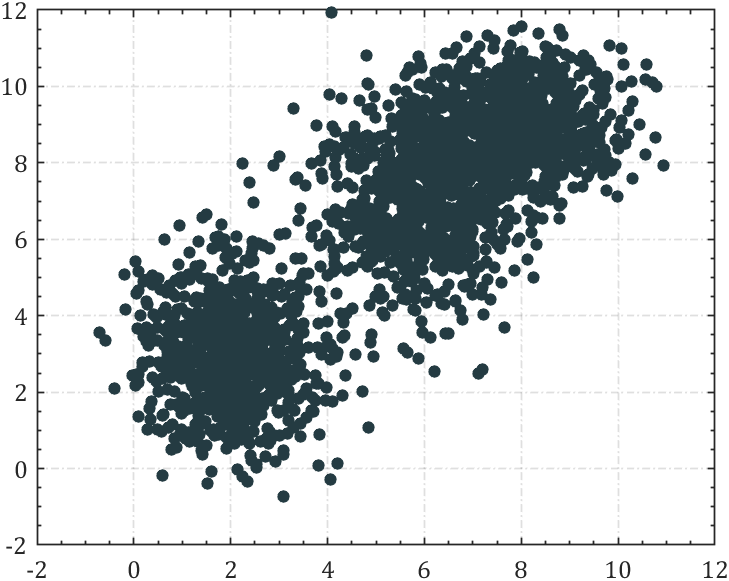
可以看到数据重叠严重，根本看不出哪里最密集，以下讲几个简单的解决数据重叠的方法。

---

1 设置透明度

这个就很简单，设置MarkerFaceAlpha即可：

% 使用scatter绘图
scatter(X,Y,'filled','CData',[36,59,66]./255,'MarkerFaceAlpha',.5);% 简单修饰，可省略
defualtAxes()

---

2 根据密度设置CData

分割网格计算核密度，可以自行调整网格划分格子数，然后通过插值计算每个点所处位置核密度并将其映射为颜色：

% 横竖分割一百格计算核密度
n=100;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 使用scatter绘图
scatter(X,Y,'filled','CData',H);% 简单修饰，可省略
defualtAxes()

当然可以通过colormap设置其他配色：

colormap(summer)

自己随便弄个配色：

CM=[0.2700         0    0.33000.2700    0.2300    0.51000.1900    0.4100    0.56000.1200    0.5600    0.55000.2100    0.7200    0.47000.5600    0.8400    0.27000.9900    0.9100    0.1300];
colormap(CM)

颜色有点不连续了，插一下值：

CM=[0.2700         0    0.33000.2700    0.2300    0.51000.1900    0.4100    0.56000.1200    0.5600    0.55000.2100    0.7200    0.47000.5600    0.8400    0.27000.9900    0.9100    0.1300];
CMX=linspace(0,1,size(CM,1));
CMXX=linspace(0,1,256)';
CM=[interp1(CMX,CM(:,1),CMXX,'pchip'),...interp1(CMX,CM(:,2),CMXX,'pchip'),...interp1(CMX,CM(:,3),CMXX,'pchip')];
colormap(CM)

---

3 等高线

还是上面的核密度计算方法，然后直接画为等高线：

% 横竖分割一百格计算核密度
n=100;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 绘制等高线图及散点图
hold on
scatter(X,Y,1,'filled','CData',[36,59,66]./255);
contour(XMesh,YMesh,ZMesh,20,'LineWidth',.8)% 简单修饰，可省略
defualtAxes()

---

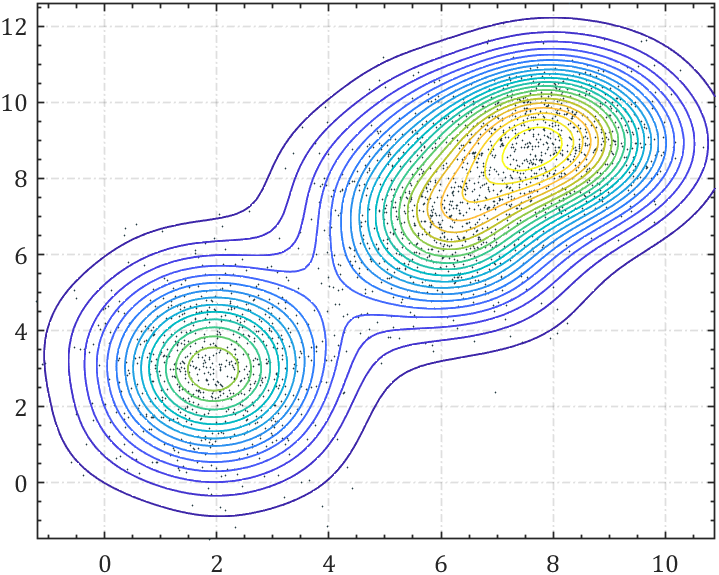
4 等高线填充

还是和上面几乎一样：

% 横竖分割一百格计算核密度
n=100;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
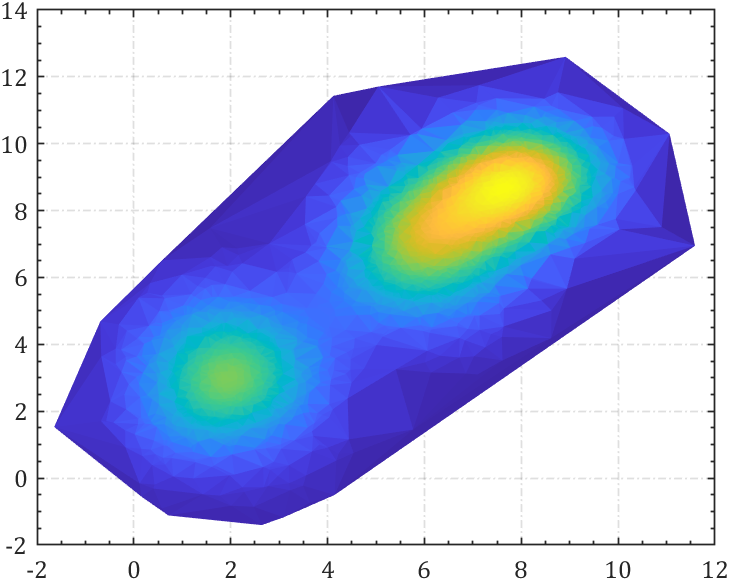
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 绘制等高线填充图
hold on
contourf(XMesh,YMesh,ZMesh,15,'EdgeColor','none')

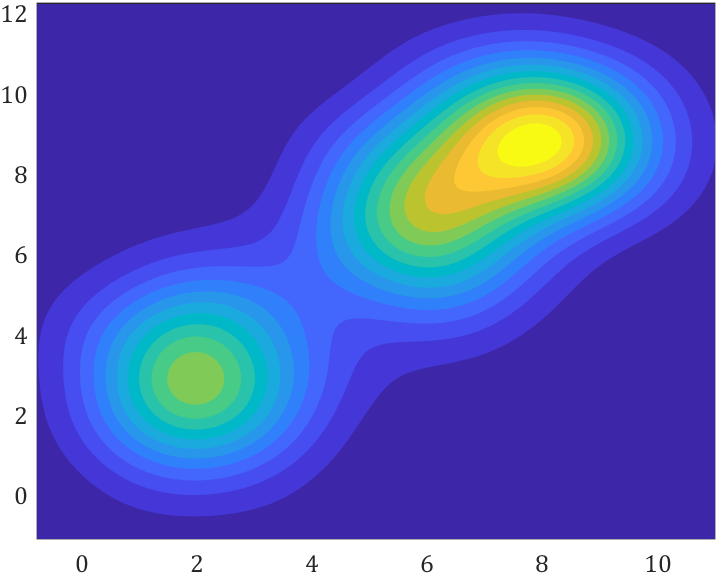
我们设置小于一定值就不画了，这里设置为1e-3可自行调整：

% 横竖分割一百格计算核密度
n=100;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 绘制等高线填充图
hold on
levels=linspace(1e-3,max(max(H)),15);
contourf(XMesh,YMesh,ZMesh,levels,'EdgeColor','none')

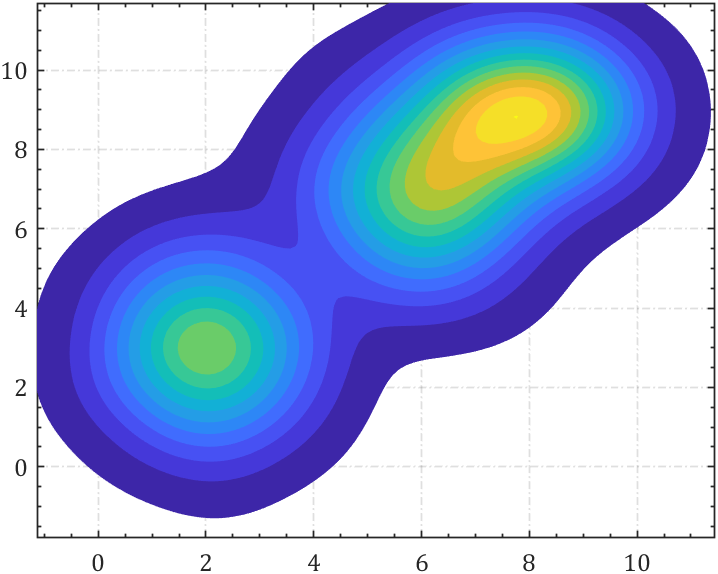
依旧改一下配色：

colormap(turbo)

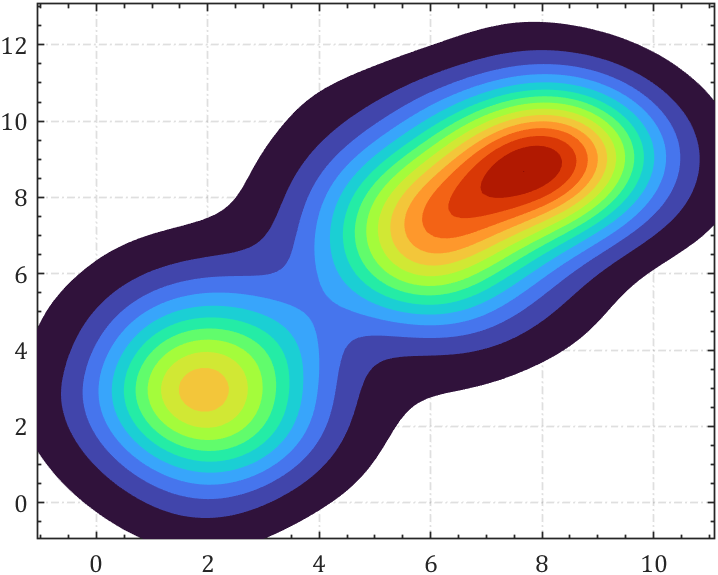
也可以用自己配色，怕乱直接把这部分完整代码放在一起：

% 横竖分割一百格计算核密度
n=100;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 绘制等高线填充图
hold on
levels=linspace(1e-3,max(max(H)),15);
contourf(XMesh,YMesh,ZMesh,levels,'EdgeColor','none')
scatter(X,Y,1,'filled','CData',[36,59,66]./255);% 设置colomap
% colormap(turbo)
CM=[0.2700         0    0.33000.2700    0.2300    0.51000.1900    0.4100    0.56000.1200    0.5600    0.55000.2100    0.7200    0.47000.5600    0.8400    0.27000.9900    0.9100    0.1300];
CMX=linspace(0,1,size(CM,1));
CMXX=linspace(0,1,256)';
CM=[interp1(CMX,CM(:,1),CMXX,'pchip'),...interp1(CMX,CM(:,2),CMXX,'pchip'),...interp1(CMX,CM(:,3),CMXX,'pchip')];
colormap(CM)% 简单修饰，可省略 
defualtAxes()

---

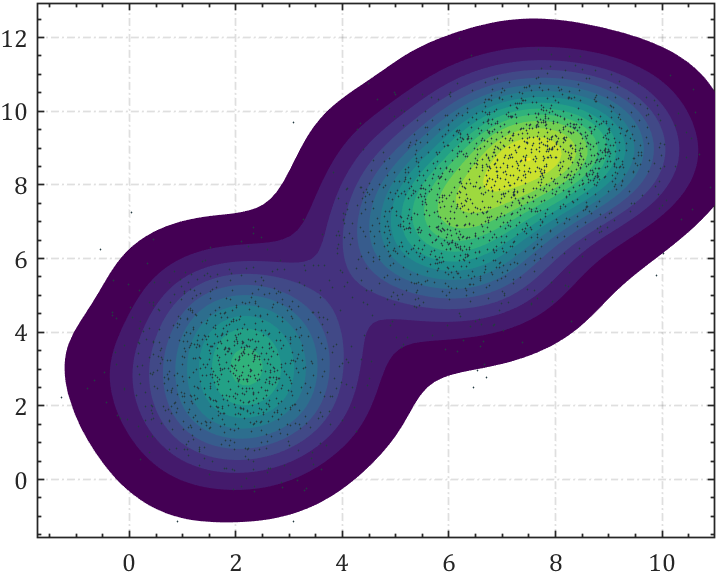
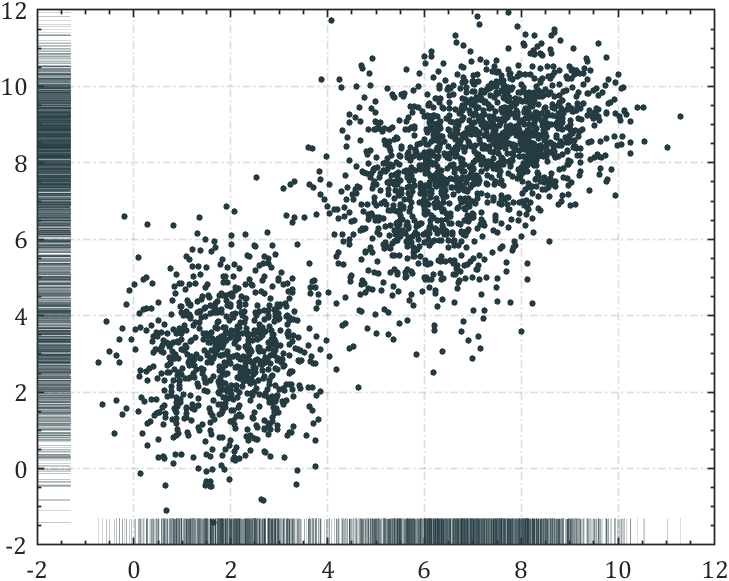
5 rug图

就是边缘加一些竖线状散点，就有点像地毯的边缘：

% 使用scatter绘图
hold on
scatter(X,Y,10,'filled','CData',[36,59,66]./255);% 绘制边际线条状散点(rug图)
ax=gca;
XLim=ax.XLim;YLim=ax.YLim;
X=X(:)';Y=Y(:)';
LXX=[X;X;X.*nan];
LXY=[Y.*0+YLim(1);Y.*0+YLim(1)+(diff(YLim))/20;Y.*nan];
plot(LXX(:),LXY(:),'Color',[[36,59,66]./255,.3]);LYY=[Y;Y;Y.*nan];
LYX=[X.*0+XLim(1);X.*0+XLim(1)+(diff(XLim))/20;X.*nan];
plot(LYX(:),LYY(:),'Color',[[36,59,66]./255,.3]);% 简单修饰，可省略
defualtAxes()

---

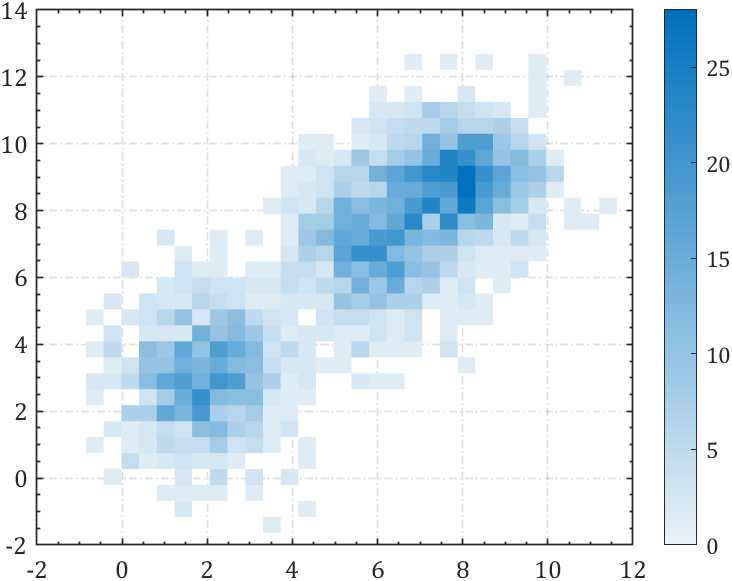
6 分bin图

这里横竖都分为30块：

% 分X,Y30块的分bin图
binscatter(X,Y,[30 30])
colorbar% 简单修饰，可省略
defualtAxes()

---

7 柱状图

在分bin图格子里画一些柱状图：

% 绘制散点图及柱状图
hold on
bcHdl=binscatter(X,Y,[20,20],'Visible','off');
scatter(X,Y,1,'filled','CData',[36,59,66]./255);
XMean=(bcHdl.XBinEdges(1:end-1)+bcHdl.XBinEdges(2:end))./2;
YMean=(bcHdl.YBinEdges(1:end-1)+bcHdl.YBinEdges(2:end))./2;
XSep=diff(bcHdl.XBinEdges(1:2));
YSep=diff(bcHdl.YBinEdges(1:2));
for i=1:size(bcHdl.Values,1)for j=1:size(bcHdl.Values,2)fill([-1,-1,1,1].*XSep./3+XMean(i),...[1,0,0,1].*YSep.*bcHdl.Values(i,j)./max(max(bcHdl.Values)).*.95+YMean(j),...[36,59,66]./255,'FaceAlpha',.9,'EdgeColor','none')end
end% 简单修饰，可省略
defualtAxes()

---

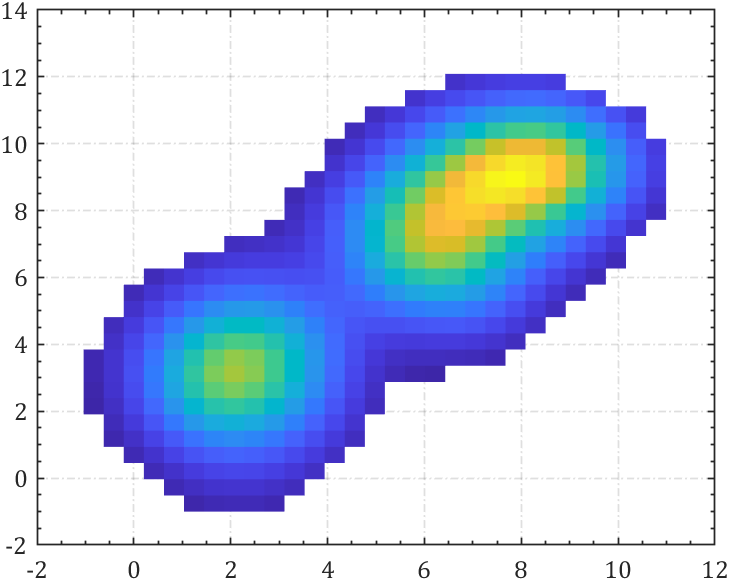
8 surf曲面

类似分bin图，不过这里不是数量统计，而是核密度:

% 横竖分割计算核密度
n=30;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 绘制surf曲面
hold on
ZMesh(ZMesh<1e-3)=nan;
surf(XMesh,YMesh,ZMesh,'EdgeColor','none');% 加一行[1,1,1]把小数值设置为白色
colormap(parula)% 简单修饰，可省略
defualtAxes()

---

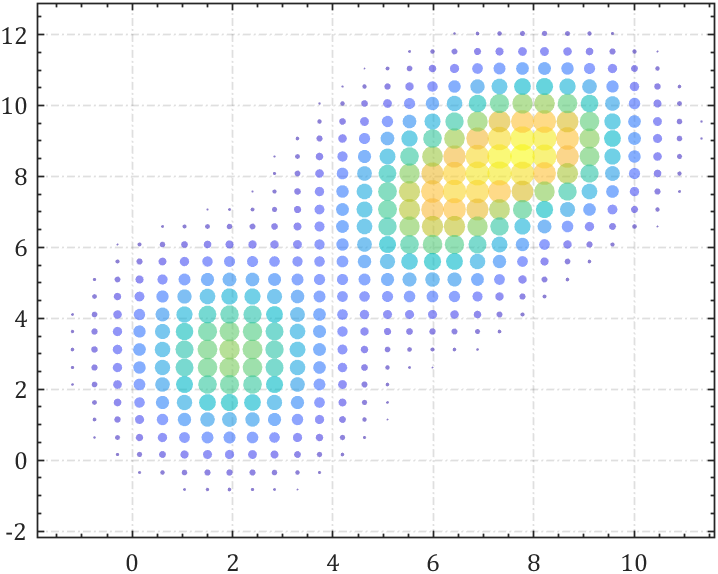
9 气泡图

还是类似的，不过换成了bubble气泡图：

% 横竖分割计算核密度
n=30;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 绘制气泡图
ZMesh(ZMesh<1e-3)=nan;
bubblechart(XMesh(:),YMesh(:),ZMesh(:),ZMesh(:),'MarkerEdgeColor','none')
bubblesize([1,12])% 简单修饰，可省略
defualtAxes()

---

10 花里胡哨没用的三角剖分

% 横竖分割一百格计算核密度
n=100;
XList=linspace(min(X),max(X),n);
YList=linspace(min(Y),max(Y),n);
[XMesh,YMesh]=meshgrid(XList,YList);
F=ksdensity([X,Y],[XMesh(:),YMesh(:)]);
ZMesh=reshape(F,size(XMesh));
H=interp2(XMesh,YMesh,ZMesh,X,Y);% 没啥用的三角化插值绘图
hold on
DT=delaunay(X,Y);
Z=(H(DT(:,1),:)+H(DT(:,2),:)+H(DT(:,3),:))./3;
trisurf(DT,X,Y,X.*0,'CData',Z,'EdgeColor','none')% 简单修饰，可省略
defualtAxes()