2024科技文化节程序设计竞赛
补题链接
https://www.luogu.com.cn/contest/178895#problems
A. 签到题
忽略掉大小为1的环,答案是剩下环的大小和减环的数量
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e6;
int n,a[N+5],cnt[N],ans;
bool vis[N];
int main(){sci(n);assert(1<=n && n<=N);rep(i,1,n){sci(a[i]);cnt[a[i]]++;}rep(i,1,n){assert(cnt[i]==1);}rep(i,1,n){if(a[i]==i || vis[i])continue;ans--;for(int j=i;!vis[j];j=a[j]){vis[j]=1;ans++;}}pte(ans);return 0;
}E. 旅行(构造)
考虑怎么把一个点连的边都用完,然后递归到n-1个点的情况即可
这里的做法是,从1号点开始走,先去3再回来,再去4再回来,直到去n再回来
然后从1去2,然后解决n-1个点的情况,然后从2回1
递归
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e6,M=N+5;
int c,n;
vector<int>p;
void sol(int x){p.pb(x);rep(i,x+2,n){p.pb(i);p.pb(x);}if(x+1<=n){sol(x+1);p.pb(x);}
}
int main(){sci(n);assert(2<=n && n<=1000);sol(1);int sz=SZ(p);rep(i,0,sz-1){printf("%d%c",p[i]," \n"[i==sz-1]);}return 0;
}for循环
注意到剩的i+1到i的边不必急着回来,可以最后从n->n-1->...->1统一回来
// 这是一份标程#include<iostream>
using namespace std;int main() {int n; cin >> n;for(int i = 1; i <= n; i++) {cout << i << ' ';for(int j = i + 2; j <= n; j++) {cout << j << ' ' << i << ' ';}}for(int i = n - 1; i > 0; i--) {cout << i << ' ';}return 0;
}I. 三元环计数(组合数学/bitset)
我是不动脑子没有视力的算竞选手,看到三元环当然是bitset大力出奇迹啦
注意到题目给的竞赛图,也就是任意两个点之间都有边
所以任取三个点,只有两种情况,
一种是三元环,
一种是存在一个点a,a指向b,a指向c
用C(n,3)减去第二种情况即可
组合数学
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=4e3+10;
int t,n,v;
char s[N];
ll ans;
int main(){sci(n);assert(3<=n && n<=4000);ans=1ll*n*(n-1)*(n-2)/6;rep(i,1,n){scanf("%s",s+1);int m=strlen(s+1);assert(m==n);int v=0;rep(j,1,n){v+=(s[j]-'0');}ans-=1ll*v*(v-1)/2;}ptlle(ans);return 0;
}bitset
n=4000,O(n^3/w)也能过真是大力出奇迹了…
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=4e3+10;
int n;
bitset<N>a[N],b[N];
char s[N];
ll ans;
int main(){ sci(n);assert(3<=n && n<=4000);rep(i,1,n){scanf("%s",s+1);rep(j,1,n){assert(s[i]!='1');if(s[j]=='1')a[i].set(j);else{if(i!=j)b[i].set(j);}}}rep(i,1,n){rep(j,1,n){if(a[i].test(j))ans+=(b[i]&a[j]).count();//printf("i:%d j:%d ans:%lld\n",i,j,ans);}}ptlle(ans/3);return 0;
}B. 魔杖(dp)
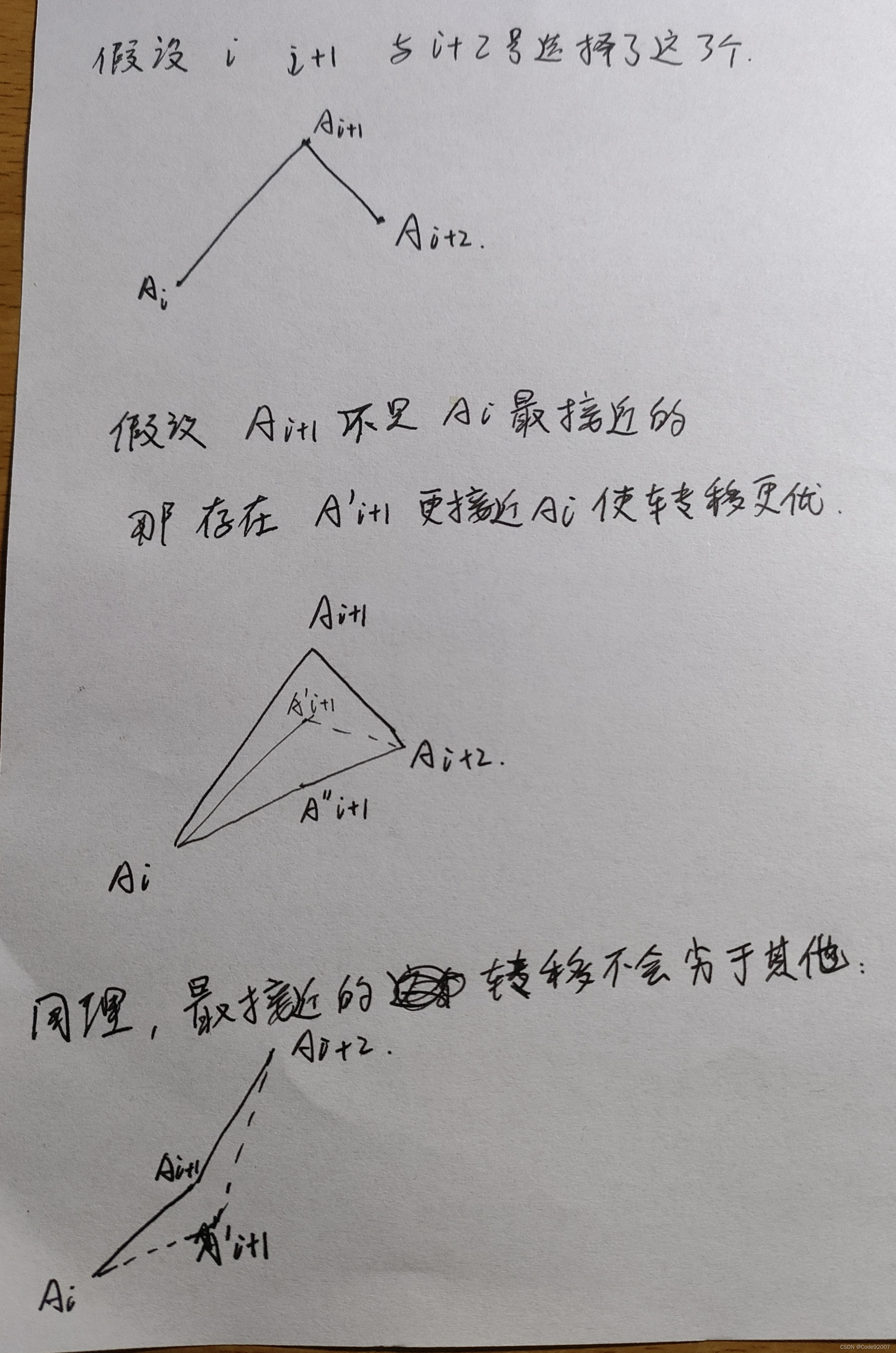
注意到每个值只可能由上一行与这个值最相邻的两个值转移,复杂度O(nm)
也就是要么从小于等于里最大的转移,要么从大于等于里最小的转移
朴素dp
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=105,M=2e4+10;
const ll INF=0x3f3f3f3f3f3f3f3fll;
int n,m,a[N][M];
ll dp[N][M];
int main(){sci(n);sci(m);assert(2<=n && n<=100 && 1<=m && m<=2e4);rep(i,1,n){rep(j,1,m){sci(a[i][j]);assert(1<=a[i][j] && a[i][j]<=1e9);}sort(a[i]+1,a[i]+m+1); }memset(dp,INF,sizeof dp);rep(i,1,m)dp[1][i]=0;rep(i,2,n){int p=1;rep(j,1,m){while(p<=m && a[i-1][p]<=a[i][j])p++;//printf("i:%d j:%d p:%d\n",i,j,p);for(auto &x:{p-1,p}){if(1<=x && x<=m){dp[i][j]=min(dp[i][j],dp[i-1][x]+abs(a[i][j]-a[i-1][x]));}}//printf("i:%d j:%d dp:%lld\n",i,j,dp[i][j]);}}ptlle(*min_element(dp[n]+1,dp[n]+m+1));return 0;
}如果没有注意到这个性质的话,可以用线段树或单调队列优化转移
但是注意到从上一行比当前值小的转移,就是dp[i][k]=min(dp[i-1][j]+a[i][k]-a[i-1][j])
从上一行比当前值大的转移,就是dp[i][k]=min(dp[i-1][j]+a[i-1][j]-a[i][k])
所以分别,正序双指针维护上一行dp[i-1][j]-a[i-1][j],逆序双指针维护上一行dp[i-1][j]+a[i-1][j]
双指针dp
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=105,M=2e4+10;
const ll INF=0x3f3f3f3f3f3f3f3fll;
int n,m,a[N][M];
ll dp[N][M];
int main(){sci(n);sci(m);assert(2<=n && n<=100 && 1<=m && m<=2e4);rep(i,1,n){rep(j,1,m){sci(a[i][j]);assert(1<=a[i][j] && a[i][j]<=1e9);}sort(a[i]+1,a[i]+m+1); }memset(dp,INF,sizeof dp);rep(i,1,m)dp[1][i]=0;rep(i,2,n){int p=1;ll now=1e18;rep(j,1,m){while(p<=m && a[i-1][p]<=a[i][j]){now=min(now,dp[i-1][p]-a[i-1][p]);p++;}dp[i][j]=min(dp[i][j],now+a[i][j]);}p=m;now=1e18;per(j,m,1){while(p>=1 && a[i-1][p]>=a[i][j]){now=min(now,dp[i-1][p]+a[i-1][p]);p--;}dp[i][j]=min(dp[i][j],now-a[i][j]);}}ptlle(*min_element(dp[n]+1,dp[n]+m+1));return 0;
}G. 回忆(扫描线入门题)
首先保证两个区间有交集,
按端点排个序然后扫描线,在l的时候把线段加进multiset,r之后删掉
然后答案分两种,相交的和包含的
相交的,[1,50]和[10,100],答案=(100-1)-(50-10)=100+10-(1+50)
就是两端点之和减去multiset里最小的两端点之和
然后包含的是两端点之差减最小之差,
包含的情况是之前加的线段的右端点更靠右,
形如[1,100]和[10,50],是100-1-(50-10)
所以用multiset里最大的两端点之差减当前两端点之差
当然可以用线段树之类的数据结构写,但感觉没必要
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=2e5+10,M=2*N;
int n,l[N],r[N],x[M],c,ans;
vector<int>add[M],del[M];
multiset<int>in,in2;
int main(){sci(n);assert(1<=n && n<=200000);rep(i,1,n){sci(l[i]),sci(r[i]);assert(1<=l[i] && l[i]<=r[i] && r[i]<=100000000);x[c++]=l[i];x[c++]=r[i];}sort(x,x+c);c=unique(x,x+c)-x;rep(i,1,n){l[i]=lower_bound(x,x+c,l[i])-x;r[i]=lower_bound(x,x+c,r[i])-x;add[l[i]].pb(i);del[r[i]].pb(i);}rep(i,0,c-1){for(auto &v:add[i]){int w=x[l[v]]+x[r[v]];int w2=x[r[v]]-x[l[v]];if(!in.empty()){ans=max(ans,w-(*in.begin()));}if(!in2.empty()){ans=max(ans,(*in2.rbegin())-w2);//ans=max(ans,w2-(*in2.begin()));}in.insert(w);in2.insert(w2);}for(auto &v:del[i]){int w=x[l[v]]+x[r[v]];int w2=x[r[v]]-x[l[v]];in.erase(in.find(w));in2.erase(in2.find(w2));}}pte(ans);return 0;
}H. 简单的平方串(kmp/exkmp/哈希)
枚举S+R的一半有多长,转化成判断s的[1,i]和[i+1,n]后者是否是前者的前缀的问题
这里是用exkmp求extend[i],当然这个玩意kmp也可以求,哈希也可以
如果S+R的一半已经超过了S原来的长度,
说明后面可以任意补a-z的字符,需要预处理26的幂的前缀和
kmp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;
const int N = 2e6 + 10;
const int M = 5e6 + 10;int p26[M], pmt[N];int main(int argc, char *argv[]) {if(argc == 3) {freopen(argv[1] + 1, "rb", stdin);freopen(argv[2] + 1, "wb", stdout);}ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);p26[0] = 1;for(int i = 1; i < M; i++) {p26[i] = (26LL * p26[i - 1] + 1) % mod;}int T; cin >> T;while(T--) {string s;int x, ans = 0;cin >> s >> x;if(x >= s.length()) ans = p26[(x - s.length()) / 2];for(int i = 1, j = 0; i < s.length(); i++) {while(j && s[i] != s[j]) j = pmt[j];j += (s[j] == s[i]);pmt[i + 1] = j;}for(int i = pmt[s.length()]; i; i = pmt[i]) {if(i <= s.length() / 2 && x >= s.length() - i * 2) ans++;}ans %= mod;cout << ans << '\n';}return 0;
}exkmp
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=2e6+10,M=5e6+10,mod=998244353;
int t,x,n,sum[M];
int net[N],ex[N];
char s[N];
void extkmppre(char s[],int len){int i=0,j,pos;net[0]=len;while(i+1<len&&s[i]==s[i+1])i++;net[1]=i,pos=1;rep(i,2,len-1){if(net[i-pos]+i<net[pos]+pos){net[i]=net[i-pos];}else{j=net[pos]+pos-i;if(j<0)j=0;while(i+j<len&&s[j]==s[i+j])j++;net[i]=j,pos=i;}}
}
void extkmp(char s1[],char s2[],int l1,int l2){int i=0,j,pos;extkmppre(s2,l2);while(i<l2&&i<l1&&s1[i]==s2[i])i++;ex[0]=i,pos=0;rep(i,1,l1-1){if(net[i-pos]+i<ex[pos]+pos){ex[i]=net[i-pos];}else{j=ex[pos]+pos-i;if(j<0)j=0;while(i+j<l1&&j<l2&&s1[i+j]==s2[j])j++;ex[i]=j,pos=i; }}
}
int main(){sci(t);assert(1<=t && t<=200000);int bs=1;sum[0]=1;rep(i,1,M-1){bs=26ll*bs%mod;sum[i]=(sum[i-1]+bs)%mod;}int m=0;while(t--){scanf("%s",s);sci(x);n=strlen(s);assert(1<=n && n<=2000000);assert(0<=x && x<=5000000);m+=n;extkmp(s,s,n,n);int ans=0;rep(i,0,n-1){if(i+ex[i]>=n && ex[i]<=i){//len=iif(2*i<=n+x)ans++;}}if(x>=n)ans=(ans+sum[(x-n)/2])%mod;pte(ans);}assert(m<=3000000);return 0;
}哈希
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;
int p26[5000006];struct pii {ll x, y;pii(ll x = 0, ll y = 0) : x(x), y(y) {}
} ha[2000006], p[2000006];pii operator + (pii a, pii b) {return pii((a.x + b.x) % mod, (a.y + b.y) % mod);}
pii operator + (pii a, int b) {return pii((a.x + b) % mod, (a.y + b) % mod);}
pii operator * (pii a, pii b) {return pii((a.x * b.x) % mod, (a.y * b.y) % mod);}
pii operator - (pii a, pii b) {return pii((a.x - b.x + mod) % mod, (a.y - b.y + mod) % mod);}
bool operator == (pii a, pii b) {return a.x == b.x && a.y == b.y;}const pii base(131, 13331);pii gethash(int L ,int R) {return ha[R] - ha[L - 1] * p[R - L + 1];
}int main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);p26[0] = 1;for(int i = 1; i < 5000006; i++) {p26[i] = (26LL * p26[i - 1] + 1) % mod;}p[0] = {1, 1};for(int i = 1; i <= 2000000; i++) {p[i] = p[i - 1] * base;}int T; cin >> T;while(T--) {string s; int x, ans = 0;cin >> s >> x;for(int i = 0; i < s.length(); i++) {ha[i + 1] = ha[i] * base + s[i];}for(int i = (s.length() & 1); i < s.length() && i <= x; i += 2) {int len = i + s.length();len = s.length() - len / 2;if(gethash(1, len) == gethash(s.length() - len + 1, s.length())) ans++;}if(x >= s.length()) ans = (ans + p26[(x - s.length()) / 2]) % mod;cout << ans << '\n';}return 0;
}
解释
D. 地牢探索(二叉树种类数 卡特兰数)
其实不如直接暴力dp打个表找找规律

首先,分母是卡特兰数,卡特兰数是C(2n,n)/(n+1)

蓝色的是可以挂叶子的地方,对于n个点的每一种二叉树形态,都有n+1个挂叶子的地方
独立考虑每个有贡献的叶子,n个点能挂2n个儿子,已经用了n-1条边建树,所以还能挂n+1个
虽然挂完之后二叉树形态可能相同,但是产生贡献的叶子不一样
挂上叶子之后是n+1个点,所以n+1个点的所有二叉树形态总的叶子和是C(2n,n),
也就是n个点时,分子是C(2n-2,n-1)
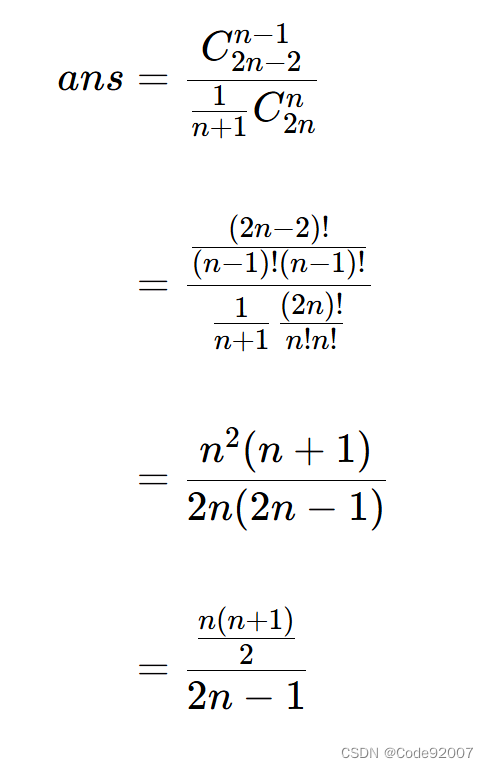
所以输出化简后的值即可,注意这个取模是2148473647,爆了int
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const ll mod=2148473647;
int n;
ll modpow(ll x,ll n,ll mod){ll res=1;for(;n;n/=2,x=1ll*x*x%mod){if(n&1)res=1ll*res*x%mod;}return res;
}
int main(){ sci(n);assert(1<=n && n<=1000000000);ll x=1ll*n*(n+1)/2;x%=mod;ll y=modpow(2ll*n-1,mod-2,mod);x=1ll*x*y%mod;ptlle(x);return 0;
}C. 静水监狱(计算几何)
判一下在凸包上还是凸包内还是凸包外,这里是用的二分,其实暴力找复杂度也够
对于在凸包内的情况,最近的距离的那条边是不会变的,
假设最近的距离是a,那么求一下时间就是
换元令u=v0+ks解一下定积分就做完了,答案是
当然可以参考一下泽与给的微分方程式子,重生之我在院赛学微分方程
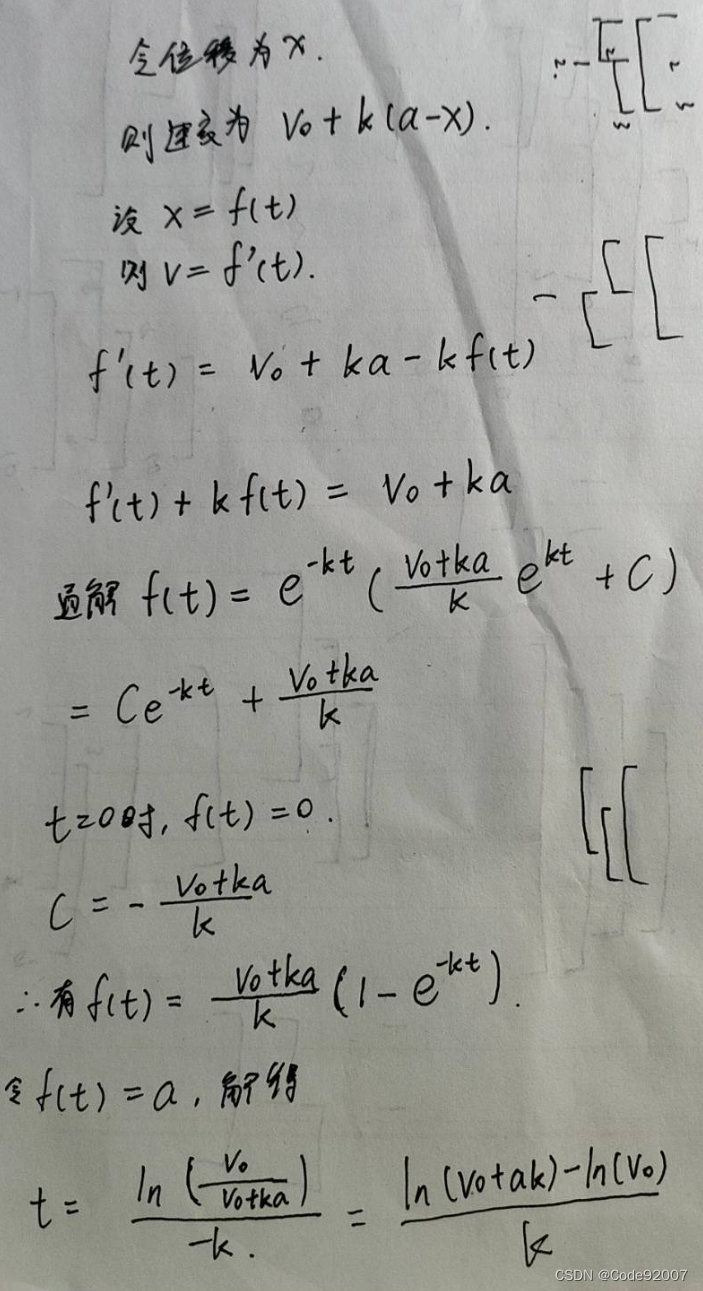
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e3+5;
struct Point{int x,y;
}p[N];
int t,n,m;
db v0,k;
ll cross(Point o,Point a,Point b){return 1ll*(a.x-o.x)*(b.y-o.y)-1ll*(a.y-o.y)*(b.x-o.x);
}
int binary(Point *p,Point &tp){//条件:p点集必须是顺时针或者逆时针//(注意3点共线下的点也必须满足这个条件)//(如果有3点共线极角序不能完成该条件)int l=0,r=n-1;while(l<r){int m=(l+r)>>1;ll c1=cross(p[0],p[m],tp);ll c2=cross(p[0],p[(m+1)%n],tp);ll c3=cross(p[m],p[(m+1)%n],tp);if(c1>=0 && c2<=0 && c3>=0){if(!c3 || (m==1 && !c1) || (m==n-2 && !c2))return 0;return 1;}if(c1>=0)l=m+1;else r=m;}return -1;
}
db cal(db x,db y,db x1,db y1,db x2,db y2){db cross = (x2 - x1) * (x - x1) + (y2 - y1) * (y - y1); if (cross <= 0)return sqrt((x - x1) * (x - x1) + (y - y1) * (y - y1)); db d2 = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1); if (cross >= d2)return sqrt((x - x2) * (x - x2) + (y - y2) * (y - y2)); db r = cross / d2; db px = x1 + (x2 - x1) * r; db py = y1 + (y2 - y1) * r; return sqrt((x - px) * (x - px) + (y - py) * (y - py));
}
int main(){sci(n);rep(i,0,n-1){sci(p[i].x),sci(p[i].y);}reverse(p,p+n);p[n]=p[0];scanf("%d%lf%lf",&m,&v0,&k);while(m--){Point tp;scanf("%d%d",&tp.x,&tp.y);int v=binary(p,tp);if(v==1){db s=1e18;rep(i,0,n-1){s=min(s,cal(tp.x,tp.y,p[i].x,p[i].y,p[i+1].x,p[i+1].y));}db ans;if(k==0)ans=s/v0;else ans=1/k*(log(v0+k*s)-log(v0));printf("%.10lf\n",ans);}else if(v==0){puts("0");}else{puts("-1");}}return 0;
}F. 感染的圣巢(树直径)
细节比较多,但整体还是有迹可循的
离线,倒着把点加回来,删点的树直径不会做,但是加点的树直径是好做的
每个被删的点,只需要考虑它往上到根这些点,最多60个,
把这60*2e5个点建出树来,剩下的树的部分不用建出来,只需要搜到对应的第一层就返回即可
因为只要底下的层数>=1,就一定能找到两个最远的儿子(比如找编号最小和最大的)
预处理这棵树每个点被删的时机,只需用父亲的被删时间和当前点的被删时间取min
先对n个点操作完之后剩的部分的树,求出直径的两个点
后面按删的时机倒着把点都加回来,时机相同时,加的时候按点号从小到大加
开map/unordered_map常数比较大会tle,所以只能把60*2e5个点加进01trie
懒得写了,直接抄泽与的代码
// 确认这份是 STD 了#include<bits/stdc++.h>
using namespace std;
typedef long long ll;const int N = 2e5 + 5;
const int M = 61 * N;ll q[N], num[M];
int cnt, ans[N], n, m;
int son[M][2], dep[M], t[M], fa[M];ll rd() {ll ret = 0; char ch = getchar();for(; isdigit(ch); ch = getchar())ret = (ret << 1) + (ret << 3) + (ch ^ 48);return ret;
} void insert(ll x, int time) {int u = 1, flag = 0;for(int i = 59; i >= 0; i--) {int temp = !!(x & (1LL << i));if(flag) {if(!son[u][temp]) {son[u][temp] = ++cnt;dep[cnt] = dep[u] + 1;num[cnt] = num[u] * 2 + temp;t[cnt] = m;fa[cnt] = u;}u = son[u][temp];}if(temp) flag = 1;}t[u] = min(t[u], time);
}int numdis(ll u, ll v) {if(u > v) swap(u, v);int i = 59, j = 59;while(!(v >> j)) j--, i--;while(!(u >> i)) i--;while(i >= 0 && ((u >> i) & 1) == ((v >> j) & 1)) i--, j--;return i + j + 2;
}int dis(int u, int v) {if(u == v) {int ret = 0;if(!son[u][0] && !son[u][1]) ret = max(ret, (n - dep[u]) * 2);else if(!son[u][0] || !son[u][1]) {ret = max(ret, (n - dep[u] - 1) * 2);if(u == 1) ret = max(ret, n - dep[u]);}return ret;}int ret = numdis(num[u], num[v]);if(!son[u][0] || !son[u][1]) ret += n - dep[u];if(!son[v][0] || !son[v][1]) ret += n - dep[v];return ret;
}vector<int> vec[N];int main(int argc, char *argv[]) {// if(argc == 3) {// freopen(argv[1] + 1, "rb", stdin);// freopen(argv[2] + 1, "wb", stdout);// }n = rd(), m = rd();dep[1] = num[1] = cnt = 1;for(int i = 1; i < M; i++) t[i] = m;for(int i = 1; i <= m; i++)q[i] = rd(), insert(q[i], i - 1);for(int i = 2; i <= cnt; i++)t[i] = min(t[i], t[fa[i]]);for(int i = 2; i <= cnt; i++) {vec[t[i]].push_back(i); }int u = 1, v = 1, d = dis(1, 1);for(int i = m; i > 0; i--) {for(int w : vec[i]) {int tu = u, tv = v, td = d, temp;if((temp = dis(w, w)) > td) tu = w, tv = w, td = temp;if((temp = dis(v, w)) > td) tu = v, tv = w, td = temp;if((temp = dis(u, w)) > td) tu = u, tv = w, td = temp;u = tu, v = tv, d = td;}ans[i] = d;}for(int i = 1; i <= m; i++) {cout << ans[i];if(i == m) cout << '\n';else cout << ' ';}return 0;
}当然可以把求lca距离的部分改成倍增,从O(n)变成O(logn),其中n是60,因为库函数近似O(1)
int lg(ll x){return 63-__builtin_clzll(x);
}
int dis(ll p,ll q){int x=lg(p),y=lg(q);if(x>y)swap(p,q),swap(x,y);q>>=(y-x);if(p==q)return y-x;per(i,6,0){int s=1<<i;if((p>>s)^(q>>s))p>>=s,q>>=s;}p>>=1;int z=lg(p);return y-z+x-z;
}相关文章:
2024科技文化节程序设计竞赛
补题链接 https://www.luogu.com.cn/contest/178895#problems A. 签到题 忽略掉大小为1的环,答案是剩下环的大小和减环的数量 #include<bits/stdc.h> #include<iostream> #include<cstdio> #include<vector> #include<map> #incl…...

玩转Easysearch语法
Elasticsearch 是一个基于Apache Lucene的开源分布式搜索和分析引擎,广泛应用于全文搜索、结构化搜索、分析等多种场景。 Easysearch 作为Elasticsearch 的国产化替代方案,不仅保持了与原生Elasticsearch 的高度兼容性,还在功能、性能、稳定性…...

【密码学】RSA公钥加密算法
文章目录 RSA定义RSA加密与解密加密解密 生成密钥对一个例子密钥对生成加密解密 对RSA的攻击通过密文来求得明文通过暴力破解来找出D通过E和N求出D对N进行质因数分解通过推测p和q进行攻击 中间人攻击 一些思考公钥密码比对称密码的机密性更高?对称密码会消失&#x…...

【ARMv8/v9 GIC 系列 5.1 -- GIC GICD_CTRL Enable 1 of N Wakeup Function】
请阅读【ARM GICv3/v4 实战学习 】 文章目录 GIC Enable 1 of N Wakeup Function基本原理工作机制配置方式应用场景小结GIC Enable 1 of N Wakeup Function 在ARM GICv3(Generic Interrupt Controller第三代)规范中,引入了一个名为"Enable 1 of N Wakeup"的功能。…...

C++怎么解决不支持字符串枚举?
首先,有两种方法:使用命名空间和字符串常量与使用 enum class 和辅助函数。 表格直观展示 特性使用命名空间和字符串常量使用 enum class 和辅助函数类型安全性低 - 编译器无法检查字符串有效性,运行时发现错误高 - 编译期类型检查…...
)
中英双语介绍四大会计师事务所(Big Four accounting firms)
中文版 “四大会计师事务所”(Big Four accounting firms)是全球最具影响力和规模最大的四家专业服务公司,它们在审计、税务、咨询和财务咨询等领域占据着主导地位。这四家公司分别是普华永道(PwC)、德勤(…...

ubuntu 查看联网配置
在Ubuntu中,你可以使用多种命令来查看联网配置。以下是一些常用的方法和命令: 查看网络接口配置: 使用 ip 命令可以查看网络接口的配置信息,包括IP地址、子网掩码等。 ip addr show或者,你也可以使用传统的 ifconfig 命…...

【数据分享】全国乡村旅游重点镇(乡)数据(Excel/Shp格式/免费获取)
之前我们分享过从我国文化和旅游部官网整理的2018-2023年我国50个重点旅游城市星级饭店季度经营状况数据(可查看之前发布的文章)!文化和旅游部官网上也分享有很多与旅游相关的常用数据,我们基于官网发布的名单文件整理得到全国乡村…...

停车场小程序的设计
管理员账户功能包括:系统首页,个人中心,车主管理,商家管理,停车场信息管理,预约停车管理,商场收费管理,留言板管理 微信端账号功能包括:系统首页,停车场信息…...
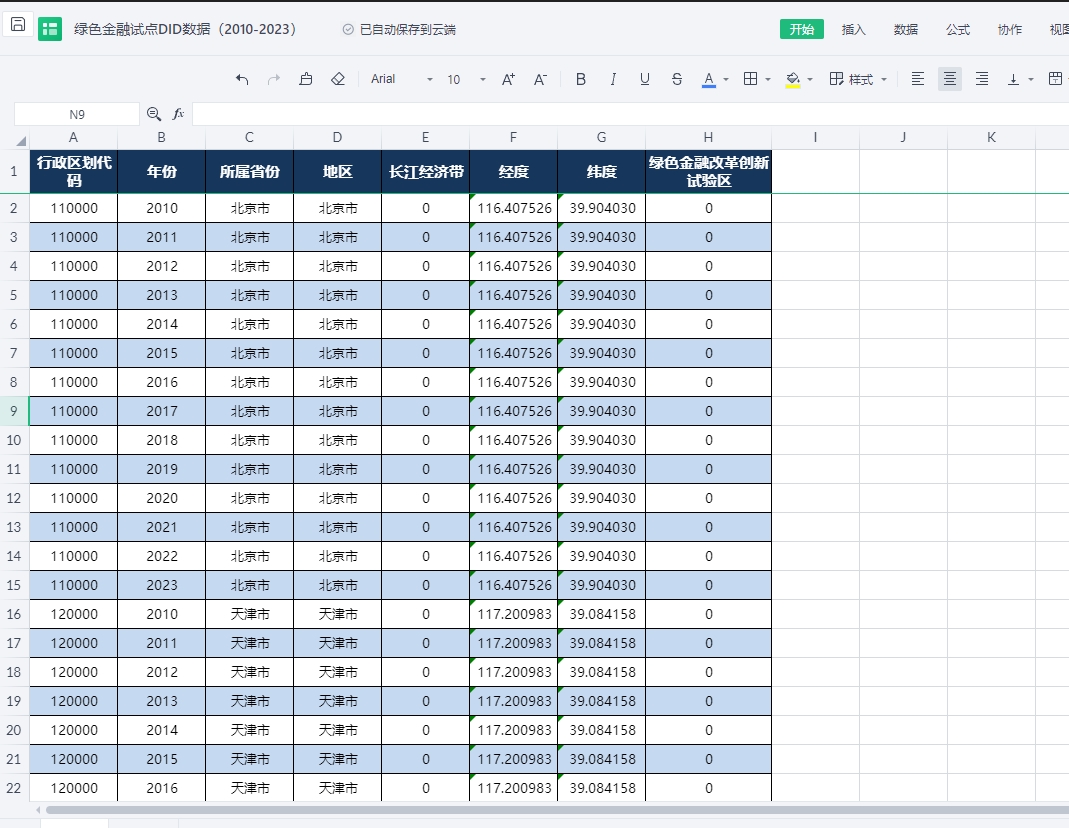
绿色金融相关数据合集(2007-2024年 具体看数据类型)
数据类型: 1.绿色债券数据:2014-2023 2.绿色信贷相关数据:2007-2022 3.全国各省及地级市绿色金融指数:1990-2022 4.碳排放权交易明细数据:2013-2024 5.绿色金融试点DID数据:2010-2023 数据来源&#…...

【matlab 项目工期优化】基于NSGA2/3的项目工期多目标优化(时间-成本-质量-安全)
一 背景介绍 本文分享了一个通用的项目工期优化的案例,决策变量是每个子项目的工期,优化目标是项目的完成时间最小,项目的总成本现值最小,项目的总安全水平最高,项目的总质量水平最高。采用的算法是NSGA2和NSGA3算法。…...

Python考前复习
选择题易错: python3不能完全兼容python2内置函数是python的内置对象之一,无需导入其他模块python中汉字变量合法,如“小李123”合法;但T-C不合法,因为有“-”集合无顺序,不能索引;range(5)[2]…...

虚拟机交叉编译基于ARM平台的opencv(ffmpeg/x264)
背景: 由于手上有一块rk3568的开发板,需要运行yolov5跑深度学习模型,但是原有的opencv不能对x264格式的视频进行解码,这里就需要将ffmpegx264编译进opencv。 但是开发板算力有限,所以这里采用在windows下,安…...

react之错误边界
错误边界实质是指什么 实际上是组件 错误边界捕获什么时候的错误 在渲染阶段的错误 错误边界捕获的是谁的错误 捕获的是子组件的错误 错误边界不能捕获什么错误 1、不能捕获异步代码 2、不能捕获事件处理函数 3、不能捕获服务端渲染 4、不能捕获自身抛出的错误 错误…...

openEuler系统之使用Keepalived+Nginx部署高可用Web集群
Linux系统之使用Keepalived+Nginx部署高可用Web集群 一、本次实践介绍1.1 本次实践简介1.2 本次实践环境规划二、keepalived介绍2.1 keepalived简介2.2 keepalived主要特点和功能2.3 使用场景三、Keepalived和Nginx介绍3.1 Nginx简介3.2 Nginx特点四、master节点安装nginx4.1 安…...

基于图像处理的滑块验证码匹配技术
滑块验证码是一种常见的验证码形式,通过拖动滑块与背景图像中的缺口进行匹配,验证用户是否为真人。本文将详细介绍基于图像处理的滑块验证码匹配技术,并提供优化代码以提高滑块位置偏移量的准确度,尤其是在背景图滑块阴影较浅的情…...

【JavaEE精炼宝库】文件操作(1)——基本知识 | 操作文件——打开实用性编程的大门
目录 一、文件的基本知识1.1 文件的基本概念:1.2 树型结构组织和目录:1.3 文件路径(Path):1.4 二进制文件 VS 文本文件:1.5 其它: 二、Java 操作文件2.1 方法说明:2.2 使用演示&…...

常用排序算法_06_归并排序
1、基本思想 归并排序采用分治法 (Divide and Conquer) 的一个非常典型的应。归并排序的思想就是先递归分解数组,再合并数组。归并排序是一种稳定的排序方法。 将数组分解最小之后(数组中只有一个元素,数组有序);然后…...
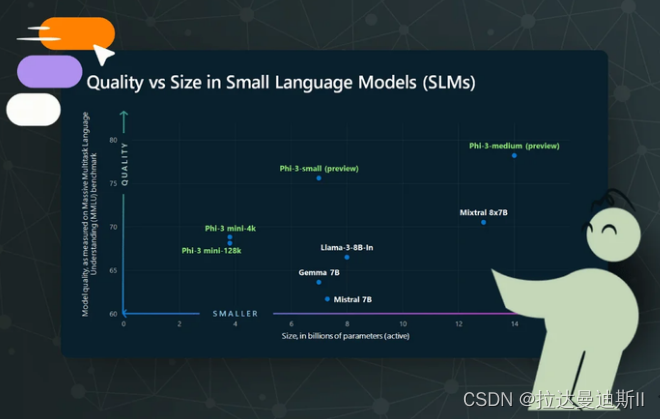
14-8 小型语言模型的兴起
过去几年,我们看到人工智能能力呈爆炸式增长,其中很大一部分是由大型语言模型 (LLM) 的进步推动的。GPT-3 等模型包含 1750 亿个参数,已经展示了生成类似人类的文本、回答问题、总结文档等能力。然而,虽然 LLM 的能力令人印象深刻…...

【Linux】:进程创建与终止
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux程序地址空间的相关知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
