线性代数基础概念:矩阵
目录
线性代数基础概念:矩阵
1. 矩阵的定义
2. 矩阵的运算
3. 矩阵的特殊类型
4. 矩阵的秩
5. 矩阵的初等变换
6. 矩阵的特征值与特征向量
7. 矩阵的应用
8. 矩阵总结
总结
线性代数基础概念:矩阵
矩阵是线性代数中的另一个重要概念,它可以用来表示线性变换、存储数据、解决线性方程组等。
1. 矩阵的定义
矩阵 是一个由数字排列成的矩形数组。
例如:
A = [ 1 2 3 ][ 4 5 6 ]
这是一个 2 行 3 列的矩阵,我们称之为 2×3 矩阵。
矩阵的元素 用 aij 表示,其中 i 表示行号,j 表示列号。
例如: 矩阵 A 中的元素 a12 = 2,a21 = 4。
2. 矩阵的运算
矩阵可以进行以下运算:
- 加法: 两个相同大小的矩阵相加,对应元素相加。
- 减法: 两个相同大小的矩阵相减,对应元素相减。
- 数乘: 一个矩阵乘以一个数,矩阵中的每个元素都乘以该数。
- 乘法: 两个矩阵相乘,需要满足一定的条件:第一个矩阵的列数必须等于第二个矩阵的行数。乘积矩阵的元素为第一个矩阵的行向量与第二个矩阵的列向量的点积。
例如:
A = [ 1 2 ][ 3 4 ]B = [ 5 6 ][ 7 8 ]A + B = [ 6 8 ][ 10 12 ]A - B = [ -4 -4 ][ -4 -4 ]2A = [ 2 4 ][ 6 8 ]AB = [ 19 22 ][ 43 50 ]
3. 矩阵的特殊类型
- 零矩阵: 所有元素都为 0 的矩阵。
- 单位矩阵: 对角线元素为 1,其他元素为 0 的方阵。
- 对角矩阵: 只有对角线元素不为 0 的方阵。
- 上三角矩阵: 对角线以下的元素都为 0 的方阵。
- 下三角矩阵: 对角线以上的元素都为 0 的方阵。
- 对称矩阵: 满足 A = AT 的方阵。
- 反对称矩阵: 满足 A = -AT 的方阵。
4. 矩阵的秩
矩阵的秩 是矩阵中线性无关的行向量或列向量的最大个数。
例如:
A = [ 1 2 3 ][ 4 5 6 ][ 7 8 9 ]
矩阵 A 的秩为 2,因为矩阵 A 中只有两行线性无关。
5. 矩阵的初等变换
矩阵的初等变换 是指对矩阵进行以下三种操作:
- 交换两行或两列。
- 将一行或一列乘以一个非零数。
- 将一行或一列加上另一行或列的倍数。
初等变换不会改变矩阵的秩。
6. 矩阵的特征值与特征向量
特征值 是一个数,它满足以下方程:
Ax = λx
其中 A 是一个矩阵,x 是一个非零向量,λ 是一个数。
特征向量 是一个非零向量 x,它满足上述方程。
特征值和特征向量是矩阵的重要性质,它们可以用来分析矩阵的性质,例如矩阵的稳定性、可对角化性等。
7. 矩阵的应用
矩阵在很多领域都有广泛的应用,例如:
- 线性方程组的求解: 矩阵可以用来表示线性方程组,并用高斯消元法求解。
- 线性变换的表示: 矩阵可以用来表示线性变换,例如旋转、平移、缩放等。
- 数据存储: 矩阵可以用来存储数据,例如图像、音频、视频等。
- 机器学习: 矩阵在机器学习中扮演着重要的角色,例如神经网络、支持向量机等。
8. 矩阵总结
| 概念 | 描述 |
|---|---|
| 矩阵 | 由数字排列成的矩形数组 |
| 矩阵的元素 | 用 aij 表示,其中 i 表示行号,j 表示列号 |
| 矩阵的运算 | 加法、减法、数乘、乘法 |
| 矩阵的特殊类型 | 零矩阵、单位矩阵、对角矩阵、上三角矩阵、下三角矩阵、对称矩阵、反对称矩阵 |
| 矩阵的秩 | 矩阵中线性无关的行向量或列向量的最大个数 |
| 矩阵的初等变换 | 交换两行或两列、将一行或一列乘以一个非零数、将一行或一列加上另一行或列的倍数 |
| 矩阵的特征值与特征向量 | 满足 Ax = λx 的数 λ 和非零向量 x |
| 矩阵的应用 | 线性方程组的求解、线性变换的表示、数据存储、机器学习 |
总结
矩阵是线性代数中的重要概念,它可以用来表示线性变换、存储数据、解决线性方程组等。理解矩阵的定义、运算、特殊类型、秩、初等变换、特征值与特征向量等概念,是学习线性代数的关键。
相关文章:

线性代数基础概念:矩阵
目录 线性代数基础概念:矩阵 1. 矩阵的定义 2. 矩阵的运算 3. 矩阵的特殊类型 4. 矩阵的秩 5. 矩阵的初等变换 6. 矩阵的特征值与特征向量 7. 矩阵的应用 8. 矩阵总结 总结 线性代数基础概念:矩阵 矩阵是线性代数中的另一个重要概念࿰…...

【优化论】约束优化算法
约束优化算法是一类专门处理目标函数在存在约束条件下求解最优解的方法。为了更好地理解约束优化算法,我们需要了解一些核心概念和基本方法。 约束优化的核心概念 可行域(Feasible Region): 比喻:想象你在一个园艺场…...

7寸微型FPV无人机技术详解
对于7寸微型FPV(First Person View,第一人称视角)无人机技术的详解,可以从以下几个方面进行介绍: 一、定义与基本概念 FPV无人机,全称为“第一人称视角无人机”,它利用安装在无人机上的摄像头…...
)
大数据面试题之Presto[Trino](2)
目录 描述Presto中的Connector是什么? Presto如何实现数据源的插件化? 如何在单机上安装Presto? 描述在集群环境中部署Presto的步骤。 如何为Presto配置JVM参数? 如何优化Presto的配置以提高性能? Presto的日…...

STM32和DHT11使用显示温湿度度(代码理解)+单总线协议
基于STM32CT,利用DHT11采集温湿度数据,在OLED上显示。一定要阅读DHT11数据手册。 1、 DHT11温湿度传感器 引脚说明 1、VDD 供电3.3~5.5V DC 2、DATA 串行数据,单总线 3、NC 空脚 4、GND 接地,电源负极 硬件电路 微…...

EVM-MLIR:以MLIR编写的EVM
1. 引言 EVM_MLIR: 以MLIR编写的EVM。 开源代码实现见: https://github.com/lambdaclass/evm_mlir(Rust) 为使用MLIR和LLVM,将EVM-bytecode,转换为,machine-bytecode。LambdaClass团队在2周…...
)
深入Django(八)
掌握Django的管理后台 引言 在前七天的教程中,我们介绍了Django的基础架构、模型、视图、模板、URL路由、表单系统以及数据库迁移。今天,我们将深入了解Django的管理后台,这是一个功能强大的内置管理界面,用于创建、更新、查看和…...

华为开发者大会2024纪要:鸿蒙OS的全新篇章与AI大模型的革命
华为开发者大会2024纪要:鸿蒙OS的全新篇章与AI大模型的革命 在科技的浪潮中,华为再次引领潮流,2024年的开发者大会带来了一系列令人瞩目的创新成果。从鸿蒙操作系统的全新Beta版到盘古大模型的震撼发布,华为正以前所未有的速度重塑智能生态。以下是本次大会的亮点,让我们…...

吴恩达深度学习笔记:机器学习策略(2)(ML Strategy (2)) 2.7-2.8
目录 第三门课 结构化机器学习项目(Structuring Machine Learning Projects)第二周:机器学习策略(2)(ML Strategy (2))2.7 迁移学习(Transfer learning) 第三门课 结构化机器学习项目࿰…...

云计算渲染时代:选择Blender或KeyShot进行高效渲染
在云渲染技术日益成熟的背景下,挑选一款贴合项目需求的3D渲染软件显得尤为关键。当前,Blender与KeyShot作为业界领先的全能渲染解决方案,广受推崇。它们虽皆能创造出令人信服的逼真视觉效果,但在特色功能上各有所长。本篇文章旨在…...

html5中的iframe
HTML5中的iframe 浏览上下文是浏览器展示文档的环境,通常是一个tab标签页,一个窗体或者是浏览器页面的一部分。每个浏览上下文都有一个活动文档的源和一个记录所有展示文档的有序历史。浏览上下文的通讯被严格限制,只有两个同源的浏览器上下…...
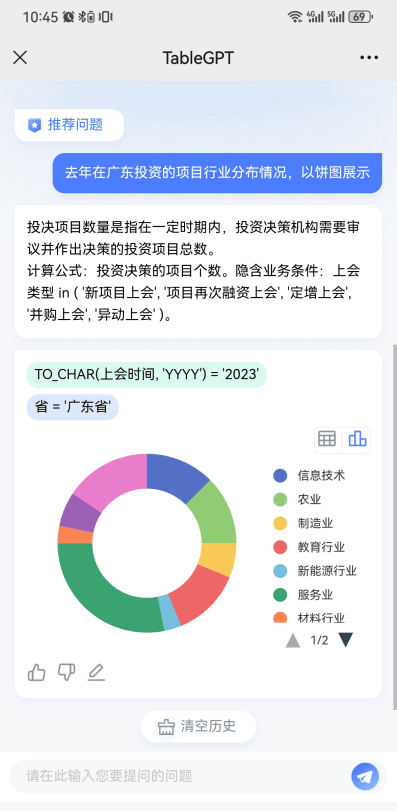
海睿思问数(TableGPT):开创企业新一代指标应用模式
1 指标建设对企业经营管理数字化的价值分析 指标是将海量数据中关键信息提炼和挖掘出来,以数据为载体展示企业经营管理和分析中的统计量。它通过分析数据,形成一个具有度量值的汇总结果,使得业务状态可以被描述、量化和分解。指标通常由度量…...

LM-Cocktail:一种创新的模型合并方法打破预训练语言模型微调后的性能局限,实现语言模型在一般任务与特定领域的均衡高性能
LM-Cocktail:一种创新的模型合并方法打破预训练语言模型微调后的性能局限,实现语言模型在一般任务与特定领域的均衡高性能 使语言模型的微调类似于调制一杯精致的鸡尾酒。模型合并可用于提高单个模型的性能。我们发现此方法对于大型语言模型和密集嵌入模型也很有用,并设计了…...
和命名导出)
默认导出(default)和命名导出
1.默认导出 优点: 简洁的导入语法: 导入时不需要使用花括号,可以直接重命名。单一职责: 模块导出一个主要功能或对象时,默认导出更符合逻辑。 适用场景: 模块只有一个导出: 如一个组件、一个…...

开发个人Go-ChatGPT--1 项目介绍
开发个人Go-ChatGPT--1 项目介绍 开发个人Go-ChatGPT--1 项目介绍知识点大纲文章目录项目地址 开发个人Go-ChatGPT–1 项目介绍 本文将以一个使用Ollama部署的ChatGPT为背景,主要还是介绍和学习使用 go-zero 框架,开发个人Go-ChatGPT的服务器后端&#…...

皮卡超级壁纸 | 幸运壁纸幸运壁纸app是一款涵盖了热门影视剧、动漫、风景等等资源的装饰工具,
软件下载链接:壁纸下载方式在链接中文章底部 皮卡超级壁纸 皮卡超级壁纸是一款专为手机用户设计的壁纸应用,它提供了丰富多样的高清壁纸资源,让用户的手机界面焕然一新。这款应用以其海量的壁纸库和用户友好的操作界面,在市场上…...
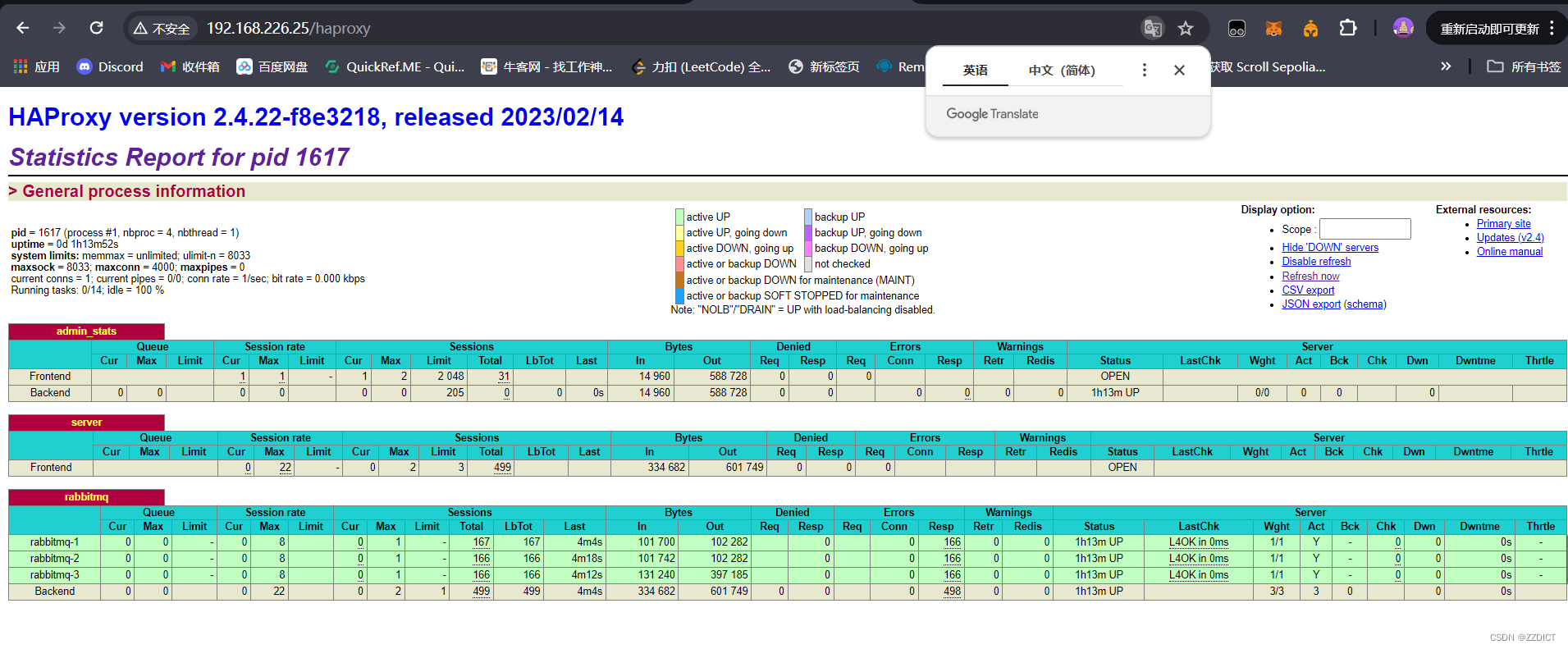
普通集群与镜像集群配置
目录 一. 环境准备 二. 开始配置集群 三. RabbitMQ镜像集群配置 四. 安装并配置负载均衡器HA 一. 环境准备 关闭防火墙和selinux,进行时间同步 主机名系统IP服务rabbitmq-1 Rocky_linux9.4 192.168.226.22RabbitMQ,MySQLrabbitmq-2Rocky_linux9.41…...
2024科技文化节程序设计竞赛
补题链接 https://www.luogu.com.cn/contest/178895#problems A. 签到题 忽略掉大小为1的环,答案是剩下环的大小和减环的数量 #include<bits/stdc.h> #include<iostream> #include<cstdio> #include<vector> #include<map> #incl…...

玩转Easysearch语法
Elasticsearch 是一个基于Apache Lucene的开源分布式搜索和分析引擎,广泛应用于全文搜索、结构化搜索、分析等多种场景。 Easysearch 作为Elasticsearch 的国产化替代方案,不仅保持了与原生Elasticsearch 的高度兼容性,还在功能、性能、稳定性…...

【密码学】RSA公钥加密算法
文章目录 RSA定义RSA加密与解密加密解密 生成密钥对一个例子密钥对生成加密解密 对RSA的攻击通过密文来求得明文通过暴力破解来找出D通过E和N求出D对N进行质因数分解通过推测p和q进行攻击 中间人攻击 一些思考公钥密码比对称密码的机密性更高?对称密码会消失&#x…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
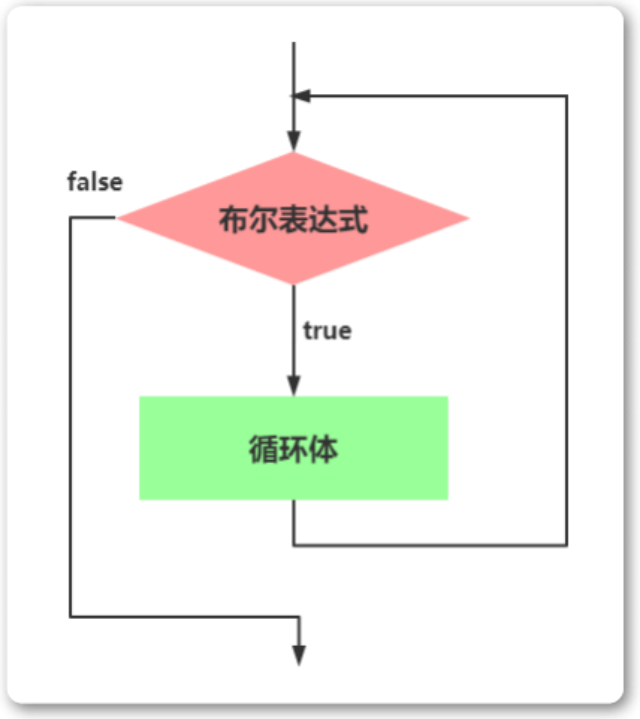
循环语句之while
While语句包括一个循环条件和一段代码块,只要条件为真,就不断 循环执行代码块。 1 2 3 while (条件) { 语句 ; } var i 0; while (i < 100) {console.log(i 当前为: i); i i 1; } 下面的例子是一个无限循环,因…...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...

EC2安装WebRTC sdk-c环境、构建、编译
1、登录新的ec2实例,证书可以跟之前的实例用一个: ssh -v -i ~/Documents/cert/qa.pem ec2-user70.xxx.165.xxx 2、按照sdk-c demo中readme的描述开始安装环境: https://github.com/awslabs/amazon-kinesis-video-streams-webrtc-sdk-c 2…...
