154. 寻找旋转排序数组中的最小值 II(困难)
154. 寻找旋转排序数组中的最小值 II
- 1. 题目描述
- 2.详细题解
- 3.代码实现
- 3.1 Python
- 3.2 Java
1. 题目描述
题目中转:154. 寻找旋转排序数组中的最小值 II


2.详细题解
该题是153. 寻找旋转排序数组中的最小值的进阶题,在153. 寻找旋转排序数组中的最小值的基础上,将严格递增数组改为非递减数组,即允许存在相同元素,建议先尝试153. 寻找旋转排序数组中的最小值并理解后再尝试本题。
如果不考虑 O ( l o g n ) O(log n) O(logn)的时间复杂度,直接 O ( n ) O(n) O(n)时间复杂度的扫描遍历一次即可。
非严格升序数组,即存在相同元素的两个值。如果不旋转则最小的数值即为第一个(索引为0)的数值,数组旋转了1到n次,寻找数组中最小的元素,这道题是二分查找的变型题。
对于严格递增的数组,假定最小值为 m i n x min_x minx,数组旋转后,假定结尾最后一个值为 t a i l tail tail,对于最小值 m i n x min_x minx,其右边的元素均小于 t a i l tail tail,而其左边的元素均大于 t a i l tail tail的值,可以利用该性质使用二分查找算法。但对于非严格递增的数组来说,由于存在相同值的情况,因此需要单独讨论。
具体算法如下:
- Step1:初始化:两个指针 l e f t left left 和 r i g h t right right,分别指向数组的起始和结束位置;
- Step2:计算中间元素的索引: m i d = ( l e f t + r i g h t ) / 2 mid = (left + right) / 2 mid=(left+right)/2;
- Step3:如果 n u m s [ m i d ] < n u m s [ r i g h t ] nums[mid] < nums[right] nums[mid]<nums[right],说明区间 ( m i d , r i g h t ] (mid, right] (mid,right]均为最小值右边的元素,故移除,更新 r i g h t = m i d right=mid right=mid,而 m i d mid mid可能为最小值,因此更新区间时不能舍弃 m i d mid mid;
- Step4:如果 n u m s [ m i d ] > n u m s [ r i g h t ] nums[mid] > nums[right] nums[mid]>nums[right],说明区间 [ l e f t , m i d ] [left, mid] [left,mid]均为最小值左边的元素,故移除,更新 l e f t = m i d + 1 left=mid+1 left=mid+1,此时 m i d mid mid值不可能为最小值,因为其已经大于了结尾值,故可舍弃 m i d mid mid;
- Step5:否则(即 n u m s [ m i d ] = n u m s [ r i g h t ] nums[mid]=nums[right] nums[mid]=nums[right]),此时难以判断是说明那个区间不包含最小值,例如 [ 3 , 3 , 3 , 1 , 2 , 3 ] 、 [ 3 , 1 , 2 , 3 , 3 , 3 , 3 ] [3,3,3,1,2,3]、[3,1,2,3,3,3,3] [3,3,3,1,2,3]、[3,1,2,3,3,3,3],但由于此时它们的值均相同,所以无论 n u m s [ r i g h t ] nums[right] nums[right] 是不是最小值,都有一个它的「替代品」 n u m s [ m i d ] nums[mid] nums[mid],因此可以忽略二分查找区间的右端点,更新 r i g h t − = 1 right-=1 right−=1。
- Step6:当指针left小于right时,重复步骤Step2_Step6;
- Step7:否则循环结束,返回 n u m s [ l e f t ] nums[left] nums[left]。
3.代码实现
3.1 Python
class Solution:def findMin(self, nums: List[int]) -> int:left, right = 0, len(nums) - 1while left < right:mid = (left + right) // 2if nums[mid] < nums[right]:right = midelif nums[mid] > nums[right]:left = mid + 1else:right -= 1return nums[left]
3.2 Java
class Solution {public int findMin(int[] nums) {int left = 0, right = nums.length - 1;while (left < right){int mid = (left + right)/2;if (nums[mid] < nums[right]){right=mid;}else if (nums[mid] > nums[right]){left = mid + 1;}else{right--;}}return nums[left];}
}
执行用时不必过于纠结,对比可以发现,对于python和java完全相同的编写,java的时间一般是优于python的;至于编写的代码的执行用时击败多少对手,执行用时和网络环境、当前提交代码人数等均有关系,可以尝试完全相同的代码多次执行用时也不是完全相同,只要确保自己代码的算法时间复杂度满足相应要求即可,也可以通过点击分布图查看其它coder的code。
相关文章:

154. 寻找旋转排序数组中的最小值 II(困难)
154. 寻找旋转排序数组中的最小值 II 1. 题目描述2.详细题解3.代码实现3.1 Python3.2 Java 1. 题目描述 题目中转:154. 寻找旋转排序数组中的最小值 II 2.详细题解 该题是153. 寻找旋转排序数组中的最小值的进阶题,在153. 寻找旋转排序数组中的最小值…...

5、MP4解复用---AAC+H264
MP4 MP4同样是一种容器格式,是由一个一个Box组成,每个Box又分为Header与Data,Data又包含很多子Box,具体的MP4文件结构也看过,内部Box结构比较复杂,一般不写MP4解释器的话,Box结构不用了解太细&a…...

计算样本之间的相似度
文章目录 前言一、距离度量1.1 欧几里得距离(Euclidean Distance)1.2 曼哈顿距离(Manhattan Distance)1.3 切比雪夫距离(Chebyshev Distance)1.4 闵可夫斯基距离(Minkowski Distance)…...

2-5 softmax 回归的简洁实现
我们发现通过深度学习框架的高级API能够使实现线性回归变得更加容易。 同样,通过深度学习框架的高级API也能更方便地实现softmax回归模型。 本节如在上节中一样, 继续使用Fashion-MNIST数据集,并保持批量大小为256。 import torch from torc…...

我 17 岁创业,今年 20 岁,月入 70 万,全靠低代码
想象一下,当你还在高中的课桌前埋头苦读时,有人告诉你三年后你将成为一家年收入超过 100 万美元的科技公司的创始人。 听起来是不是像天方夜谭? 但对于 20 岁的小伙子 Jacob Klug 来说,这就是他的真实人生。 在大多数同龄人还在为…...

【Python】已解决:urllib.error.HTTPError: HTTP Error 403: Forbidden
文章目录 一、分析问题背景二、可能出错的原因三、错误代码示例四、正确代码示例五、注意事项 已解决:urllib.error.HTTPError: HTTP Error 403: Forbidden 一、分析问题背景 在使用Python的urllib库中的urlopen或urlretrieve函数下载文件时,有时会遇到…...

昇思12天
FCN图像语义分割 1. 主题和背景 FCN是由UC Berkeley的Jonathan Long等人于2015年提出的,用于实现图像的像素级预测。 2. 语义分割的定义和重要性 语义分割是图像处理和机器视觉中的关键技术,旨在对图像中的每个像素进行分类。它在很多领域有重要应用…...

【postgresql】 基础知识学习
PostgreSQL是一个高度可扩展的开源对象关系型数据库管理系统(ORDBMS),它以其强大的功能、灵活性和可靠性而闻名。 官网地址:https://www.postgresql.org/ 中文社区:文档目录/Document Index: 世界上功能最强大的开源…...

按键控制LED流水灯模式定时器时钟
目录 1.定时器 2. STC89C52定时器资源 3.定时器框图 4. 定时器工作模式 5.中断系统 1)介绍 2)流程图:编辑 3)STC89C52中断资源 4)定时器和中断系统 5)定时器的相关寄存器 6.按键控制LED流水灯模…...

【Docker安装】OpenEuler系统下部署Docker环境
【Docker安装】OpenEuler系统下部署Docker环境 前言一、本次实践介绍1.1 本次实践规划1.2 本次实践简介二、检查本地环境2.1 检查操作系统版本2.2 检查内核版本2.3 检查yum仓库三、卸载Docker四、部署Docker环境4.1 配置yum仓库4.2 检查可用yum仓库4.3 安装Docker4.4 检查Docke…...

小程序 使用 UI 组件 Vant Weapp 、vant组件样式覆盖
注意:使用vant 包,需要把app.json 中 的"style:v2" 这句去掉 不然会出现样式混乱的问题 Vant Weapp组件库的使用 参考官网 vant官网 Vant Weapp 组件样式覆盖 Vant Weapp 基于微信小程序的机制,为开发者提供了 3 种修改组件样式…...
前端弄一个变量实现点击次数在前端页面实时更新)
(接上一篇)前端弄一个变量实现点击次数在前端页面实时更新
实现点击次数在前端页面实时更新,确实需要在前端维护一个变量来存储当前的点击次数。这个变量通常在Vue组件的data选项中定义,并在组件的生命周期方法或事件处理函数中更新。 以下是实现这一功能的基本步骤: 定义变量:在Vue组件的…...

迭代器模式在金融业务中的应用及其框架实现
引言 迭代器模式(Iterator Pattern)是一种行为设计模式,它提供了一种方法顺序访问一个聚合对象中的各个元素,而又不需要暴露该对象的内部表示。在金融业务中,迭代器模式可以用于遍历复杂的数据结构,如交易…...
浏览器插件利器-allWebPluginV2.0.0.14-stable版发布
allWebPlugin简介 allWebPlugin中间件是一款为用户提供安全、可靠、便捷的浏览器插件服务的中间件产品,致力于将浏览器插件重新应用到所有浏览器。它将现有ActiveX插件直接嵌入浏览器,实现插件加载、界面显示、接口调用、事件回调等。支持谷歌、火狐等浏…...

机器学习训练之使用静态图加速
前言 MindSpore有两种运行模式:动态图模式和静态图模式。默认情况下是动态图模式,也可以手工切换为静态图模式。 动态图模式 动态图的特点是计算图的构建和计算同时发生,符合Python的解释执行方式。在调试模型时较为方便,能够实…...
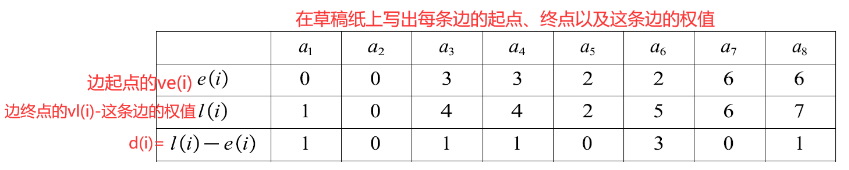
数据结构速成--图
由于是速成专题,因此内容不会十分全面,只会涵盖考试重点,各学校课程要求不同 ,大家可以按照考纲复习,不全面的内容,可以看一下小编主页数据结构初阶的内容,找到对应专题详细学习一下。 目录 …...

昇思25天学习打卡营第12天|FCN图像语义分割
文章目录 昇思MindSpore应用实践基于MindSpore的FCN图像语义分割1、FCN 图像分割简介2、构建 FCN 模型3、数据预处理4、模型训练自定义评价指标 Metrics 5、模型推理结果 Reference 昇思MindSpore应用实践 本系列文章主要用于记录昇思25天学习打卡营的学习心得。 基于MindSpo…...

昇思MindSpore学习笔记4-03生成式--Diffusion扩散模型
摘要: 记录昇思MindSpore AI框架使用DDPM模型给图像数据正向逐步添加噪声,反向逐步去除噪声的工作原理和实际使用方法、步骤。 一、概念 1. 扩散模型Diffusion Models DDPM(denoising diffusion probabilistic model) (无)条件…...

Go:hello world
开启转职->Go开发工程师 下面是我的第一个go的程序 在上面的程序介绍: 1、package main 第一行代码package main定义了包名。必须在源文件中非注释的第一行指明这个文件属于哪个包,如:package main。package main表示一个可独立执行的程…...

JVM专题之内存模型以及如何判定对象已死问题
体验与验证 2.4.5.1 使用visualvm **visualgc插件下载链接 :https://visualvm.github.io/pluginscenters.html https://visualvm.github.io/pluginscenters.html **选择对应JDK版本链接--->Tools--->Visual GC** 2.4.5.2 堆内存溢出 * **代码** java @RestCont…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
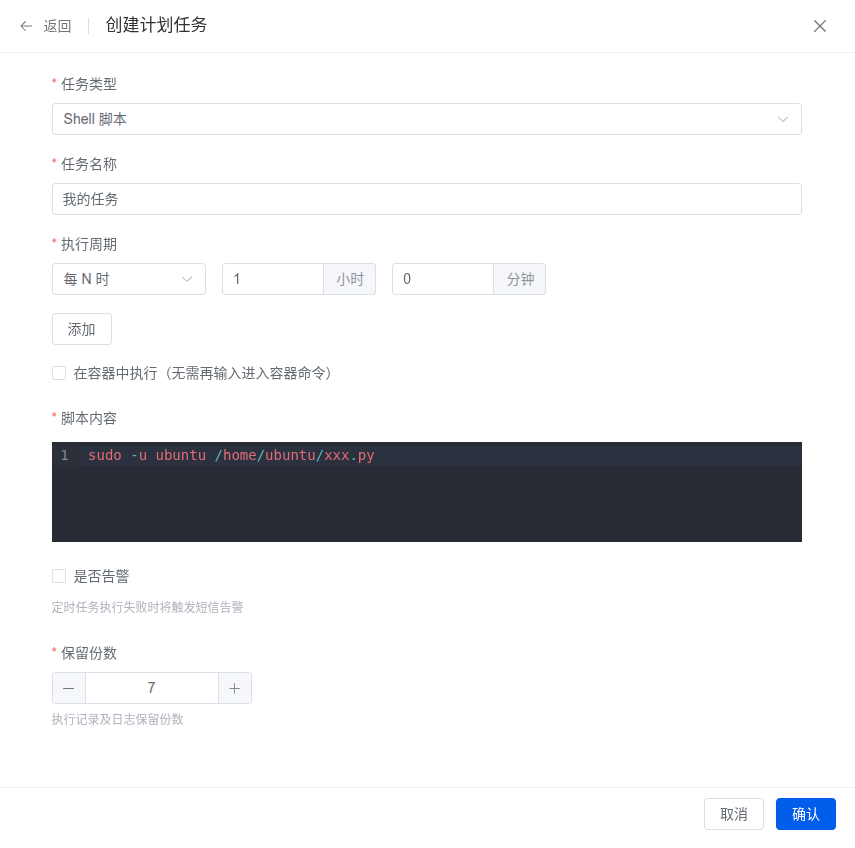
【Linux】使用1Panel 面板让服务器定时自动执行任务
服务器就是一台24小时开机的主机,相比自己家中不定时开关机的主机更适合完成定时任务,例如下载资源、备份上传,或者登录某个网站执行一些操作,只需要编写 脚本,然后让服务器定时来执行这个脚本就可以。 有很多方法实现…...

docker容器互联
1.docker可以通过网路访问 2.docker允许映射容器内应用的服务端口到本地宿主主机 3.互联机制实现多个容器间通过容器名来快速访问 一 、端口映射实现容器访问 1.从外部访问容器应用 我们先把之前的删掉吧(如果不删的话,容器就提不起来,因…...

React与原生事件:核心差异与性能对比解析
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
