数论----质数的求解(C/C++)
CSDN的uu,你们好呀,今天我们要学习的内容是数论哦!这也是算法题中的一类题目吧。记好安全带,准备发车咯!🚀
学习数论的意义📢
算法导论说:“数论曾经被视为一种虽然优美但却没什么用处的纯数学学科。如今,数论算法已经得到了广泛的使用。这很大程度上要归功于人们发明了基于大素数的加密方法。快速计算大素数的算法使得高效加密成为可能,而目前其安全性的保证则依赖于缺少高效将合数分解为大素数之积(或求解相关问题,如计算离散对数)方法的现状。” 数论可以分为:初等数论,解析数论,代数数论,几何数论等。我们从基础开始学起哦!
求解区间内的质数📗
我们先来看看质数的定义:在大于1的整数中,如果一个整数只包含1和本身两个约数,那么这个数就被称为质数或者素数。
顺便来看看约数的定义:约数(又称因数)是指若整数a除以整数b(b≠0)除得的商正好是整数而没有余数,就说a能被b整除,或b能整除a,其中a称为b的倍数,b称为a的约数。 下面我们就讲讲如何求解一个区间内的所有质数。
2.1 质数的定义求解1-N之间的质数1️⃣
在讲解这种方法之前我们需要直到如何判断一个数是否是质数。根据质数的定义,显然我们可以枚举
2-(N-1)之间数,如果某个数能被N整除,说明N不是质数。反之如果2-(N-1) 之间的数均不能被N整除那么说明N就是质数啦!

在知到了如何判断一个数是否为质数之后,想要求解1-N之间的所有质数只需要遍历 1- N 之间的所有数,用质数的判断函数对这些数进行检验输出即可!
bool isPrime(int x)
{//如果小于2非质数if (x < 2)return false;//遍历 2 - (x - 1)的所有数for (int i = 2; i < x; i++){//如果有约数,非质数if (x % i == 0)return false;}//没有约数返回falsereturn true;
}int main()
{for (int i = 1; i <= 100; i++){//是质数输出结果if (isPrime(i))printf("%d ", i);}return 0;
}
显然在 isPrime 这个函数的枚举中是可以优化的。因为一个数 i 如果能被 n整除,那么 n / i 也能够被n整除,所以我们只需要枚举较小的那个数i即可,也就是for循环结条件可以写成:
for(int i = 2; i <= x / i; i++)
这便是i<=sqrt(x) 的由来!但是这里不建议将循环的结束条件写成:i<=sqrt(x),这样写每一次循环都要进行计算,时间复杂度会提高!也不建议写成:i * i <= x,这样写可能会溢出!发生意想不到的结果。
bool isPrime(int x)
{//如果小于2非质数if (x < 2)return false;//遍历 2 - (x - 1)的所有数for (int i = 2; i <= x / i; i++){//如果有约数,非质数if (x % i == 0)return false;}//没有约数返回falsereturn true;
}int main()
{for (int i = 1; i <= 100; i++){//是质数输出结果if (isPrime(i))printf("%d ", i);}return 0;
}时间复杂度分析:在判断一个数是否为质数时,时间复杂度一定是根号x,求解的数的范围是 1-N
所以总的时间复杂度为:O(N*sqrt(N))。
2.2 筛质数----埃氏筛法2️⃣
什么是筛质数呢?就是将质数从一个区间内筛选出来!你可以将指数理解为较大的石头,合数理解为较小的石头,我们利用筛子就可以将小石头筛掉留下大石头!
第一种方法:
遍历2-N之间的所有数,将遍历到的该数的倍数(不包括自身)筛去,遍历完毕后剩下的数就是质数啦!

如何对应到代码上呢?我们用一个数组primes来存储质数,用一个数组st来判断一个数是否被筛去,然后我们遍历1-N之间的所有数,如果这个数没有被筛去,即st[i] == false,就把他添加到primes数组中!然后利用这个数将他的倍数筛去!
时间复杂度分析:

所以我们可以取时间复杂度为N*logN。
const int N = 100;
bool st[N];
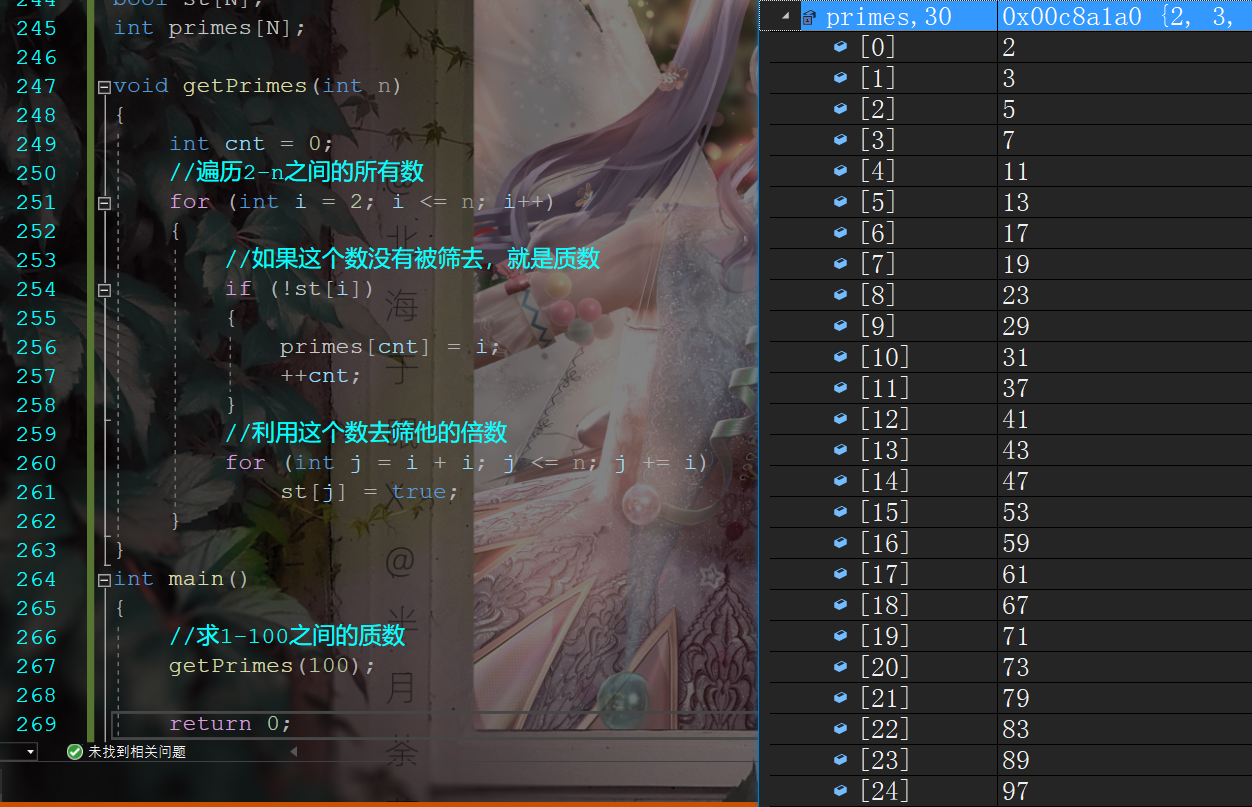
int primes[N];void getPrimes(int n)
{int cnt = 0;//遍历2-n之间的所有数for (int i = 2; i <= n; i++){//如果这个数没有被筛去,就是质数if (!st[i]){primes[cnt] = i;++cnt;}//利用这个数去筛他的倍数for (int j = i + i; j <= n; j += i)st[j] = true;}
}
int main()
{//求1-100之间的质数getPrimes(100);return 0;
}
方法一的优化:
筛选的过程中我们只需要筛掉质数的倍数即可!因为合数是可以进行质因子分解的!所以所有的合数一定会被他的质因子给筛掉!因此我们可以把筛掉倍数的循环放在里面!
const int N = 100;
bool st[N];
int primes[N];void getPrimes(int n)
{int cnt = 0;//遍历2-n之间的所有数for (int i = 2; i <= n; i++){//如果这个数没有被筛去,就是质数if (!st[i]){primes[cnt] = i;++cnt;//利用这个数去筛他的倍数for (int j = i + i; j <= n; j += i)st[j] = true;}}
}
int main()
{//求1-100之间的质数getPrimes(100);return 0;
}时间复杂度分析:
这里有一个质数定理:1-N中的质数个数有 N / lnN 个。

2.3 筛质数----线性筛法3️⃣
线性筛法是对埃氏筛法的优化哈!我们来看埃氏筛法:对于6和12这两个数,在遍历到质数2时这两个数会被筛一次,在遍历到质数3时这两个数还会再被筛一次!显然会有重复的工作!而线性筛法能够保证每一个合数只会被筛一次,这是怎么做到的呢?
我们来看这样一句话:对于一个合数X,假设primes[j] 是X的最小质因子,那么在遍历到质数primes[j] 时,这个合数X就一定会被筛去,又因为每一个合数都有且仅有一个最小质因子,所以对于每一个合数我们都用它的最小质因子来筛掉!
具体应该怎么做呢?同样我们用i遍历1-N之间的所有数,如果这个数没有被筛去,那么他就一定是质数,然后我们用j从小到大遍历存储质数的primes数组,然后筛掉primes[j] * i这个合数!为什么是primes[j] * i 呢?

那么用j遍历primes数组中的质数时循环的结束条件是什么呢?通过上面的分析,我们能够知道退出遍历primes数组的条件就是用最小质因子筛去所有可能筛掉的数!当遍历得到的质数如果比i大的话,显然就不满足用最小质因数筛合数的条件了!因此循环的结束条件可以这么写:
for(int j = 0; primes[j] <= n / i; j++)这里大家可能会有一个疑问?primes数组的访问会不会越界呢?也就是说要不要加上小于primes数组大小的限制条件呢?
emm,是没有这个必要的哈!当i为合数时,枚举到他的最小质因子后就会结束循环!当i为质数的时候,枚举到自身时也会退出循环,所以是没有必要加上这个条件的哈!
const int N = 100;
bool st[N];
int primes[N];void getPrimes(int n)
{ int cnt = 0;for (int i = 2; i <= n; i++){//这个数没有被筛去。说明他是质数if(!st[i])primes[cnt++] = i;//遍历primes数组,筛去可以筛去的合数for (int j = 0; primes[j] <= n / i; j++){//筛掉primes[j]*i这个数!st[primes[j] * i] = true;//如果说i是合数,那么找到最小质因子后就结束循环//如果说i是质数,遍历到等于自身的那个质数时也会结束循环if (i % primes[j] == 0)break;}}
}int main()
{getPrimes(100);return 0;
}
3. 埃氏筛法和线性筛法粗略的时间比较⌛
当数据量在10的6次方时两者时间相差不大,数据量在10的7次方时,埃氏筛法会比线性筛法慢一倍左右。
数据量为10^6时:

数据量为10^8时:
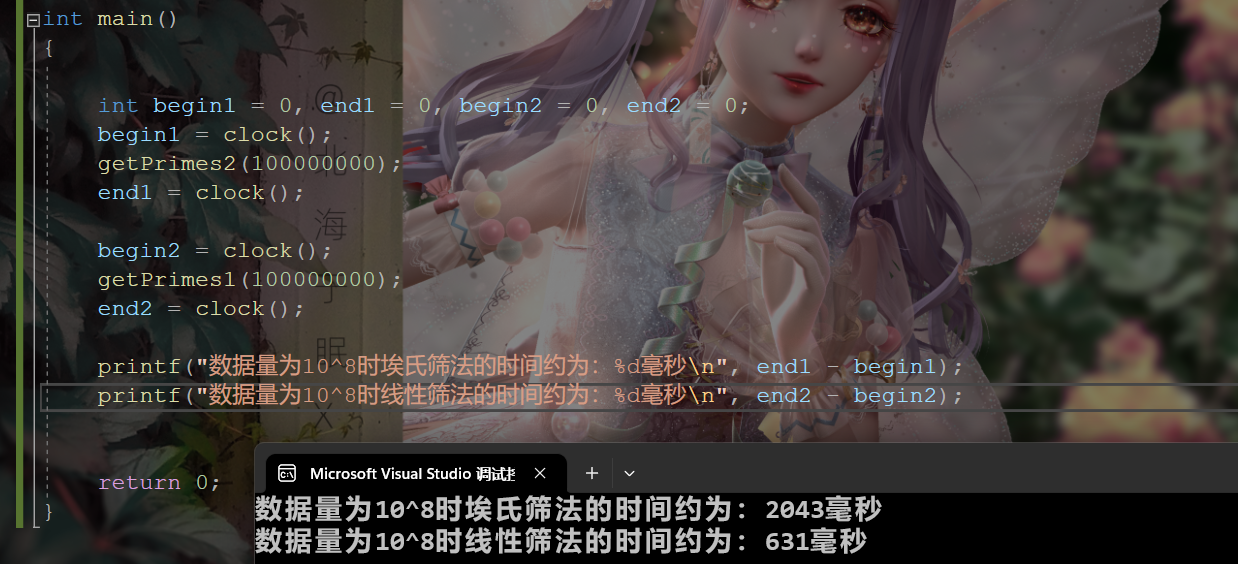
3. 小试牛刀🚩
204. 计数质数 - 力扣(Leetcode)
谢谢大家的阅读!如果有什么讲的不对的地方欢迎大家指正!💐
相关文章:

数论----质数的求解(C/C++)
CSDN的uu,你们好呀,今天我们要学习的内容是数论哦!这也是算法题中的一类题目吧。记好安全带,准备发车咯!🚀学习数论的意义📢算法导论说:“数论曾经被视为一种虽然优美但却没什么用处…...
【电赛MSP430系列】GPIO、LED、按键、时钟、中断、串口、定时器、PWM、ADC
文章目录MSP430一、GPIO二、点亮LED三、按键控制LED四、更改主时钟五、串口通信六、串口中断七、外部中断八、定时器九、定时器中断十、PWM十一、ADCMSP430 MSP430 是德州仪器(TI)一款性能卓越的超低功耗 16 位单片机,自问世以来,…...

【Linux】进程理解与学习(Ⅱ)
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹相关文章推荐:【Linux】冯.诺依曼体系结构与操作系统【Linux】进程理解与学习(Ⅰ)浅谈Linux下的shell--BASH前言章节…...

vscode 爽到起飞的快捷键
这里写目录标题1. 窗口操作2. 代码编辑3. 批量操作4. 错误处理1. 窗口操作 文件之间切换: CtrlTab 切出一个新的编辑器窗口(最多3个): Ctrl\ 切换左中右3个编辑器窗口的快捷键: Ctrl1 Ctrl2 Ctrl3 2. 代码编辑 代码格式化: ShiftAltF 向上或向下移动一行: Alt…...
vs +qt 打包.cpp和.h为DLL文件
文章目录一 编译成库1 创建一个Qt library 项目2,将已有的文件拷贝到项目目录下3 在项目中添加现有项4,拷贝头文件到需要暴露给外面使用的类的头文件中5 拷贝xxx_EXPORT的宏到需要被暴露的类的名前面6 然后点击编译 就完成了。得到的dll文件在debug里面二…...

echarts有滑块
vue下使用echarts折线图及其横坐标拖拽功能 drawLine() {let that this,lineDate [],dispatchCount [],finishCount [],newCount [];let param {// 参数};axios.post(url, param).then(function(response) {let rs response.data.data;if (rs ! undefined && rs…...

MATLAB绘制ROC曲线
ROC曲线(Receiver Operating Characteristic Curve) 1 简介 ROC曲线是用于评估二元分类模型(如Logistic回归)表现优劣的一种工具,其横轴表示假阳性率(false positive rate,FPR),即实际为负例但…...
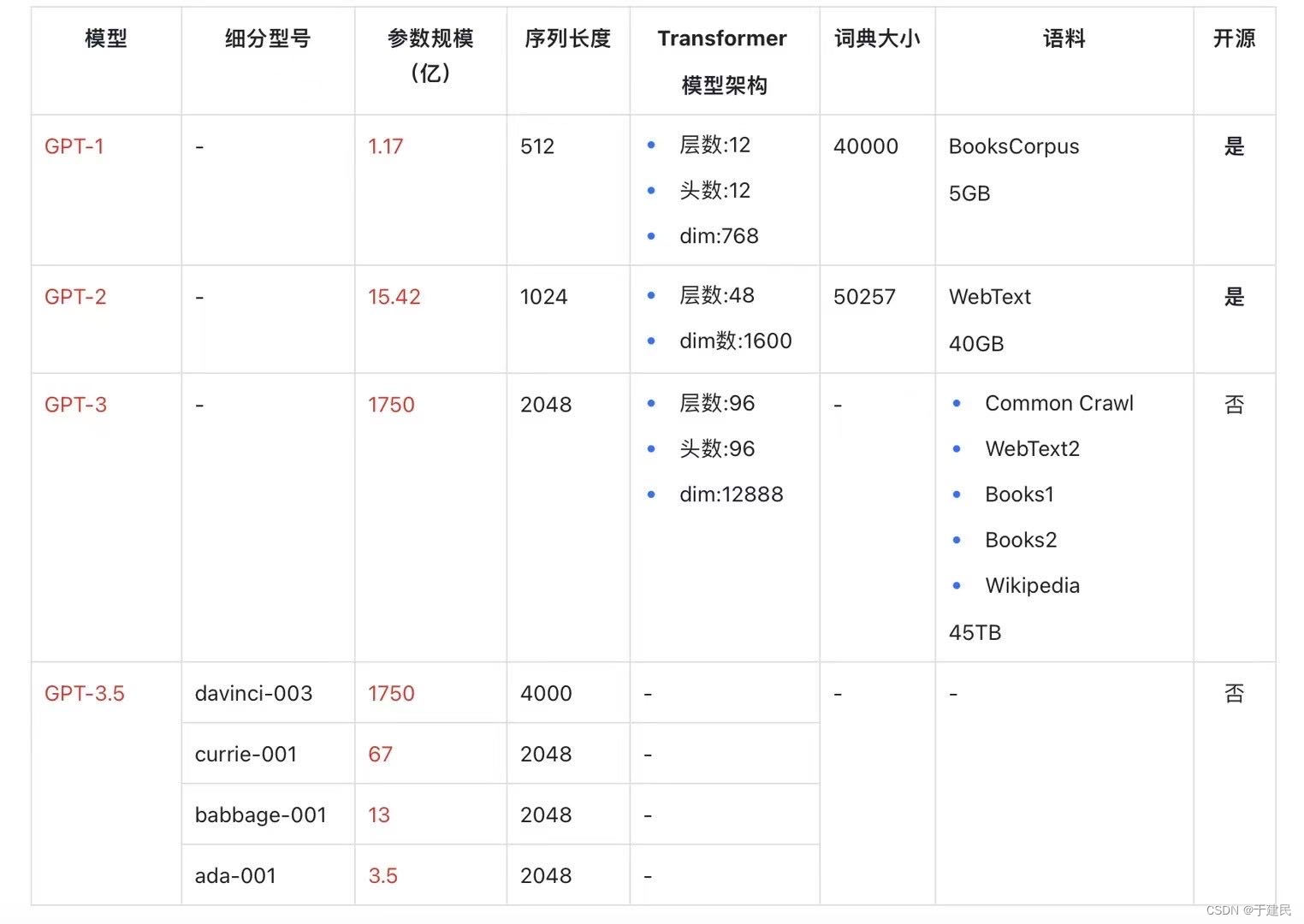
ChatGPT前传
文章目录前言GPT概述GPT-1代GPT-1 学习目标和概念介绍GPT-1 训练数据集GPT-1 模型结构和应用细节GPT-1 效果性能和总结GPT-2代GPT-2 学习目标和概念介绍GPT-2 训练数据集GPT-2 模型结构和应用细节GPT-2 性能效果和总结GPT-3代GPT-3 学习目标和概念介绍GPT-3 训练数据集GPT-3 模…...

我的十年编程路 2020年篇
我出生在1990年,2020年到来的时候,我完成了一项成就:奔三。同时,也开启了新的征程:奔四。 2020年的春节是在广州的丈母娘家度过的,春节后大概是初五,或者是初六,我和媳妇就返回天津…...

力扣-SQL【入门】
https://leetcode.cn/study-plan/sql/?progressxhqm4sjh 目录选择595. 大的国家1757. 可回收且低脂的产品584. 寻找用户推荐人183. 从不订购的客户排序 & 修改1873. 计算特殊奖金627. 变更性别196. 删除重复的电子邮箱选择 595. 大的国家 # Write your MySQL query state…...
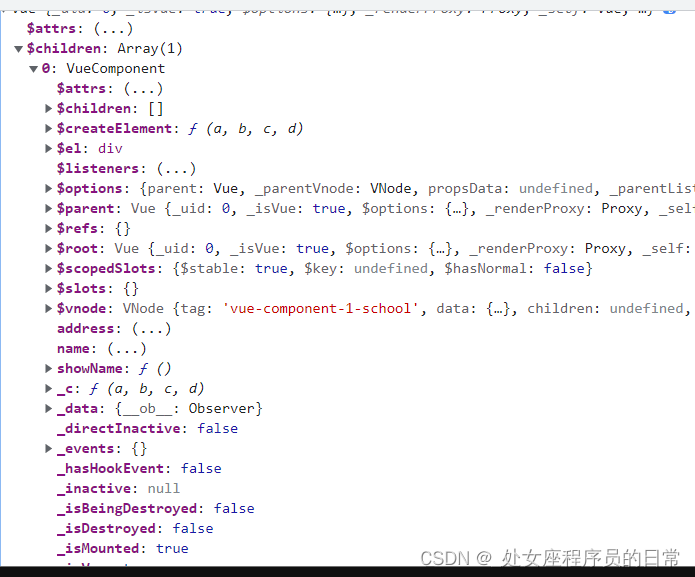
Vue中组件到底是什么
1.先说结论: Vue中组件本质是一个名为VueComponent的构造函数,且不是程序员定义的,是Vue.extend生成的。 2.我们使用组件时发生了什么? 比如定义了一个school,然后在页面上使用它 我们只需要写 < school/ > 或< school &…...

不同时间间隔数据对统计结果的影响
目录摘要1. 实测数据来源2. 数据分析方法3 结果分析3.1 波况分析摘要 采用不同的波浪观测方法所获得的波浪数据的时间间隔不一致,其数据的准确性须进行分析。基于大埕湾逐时周年波浪观测数据,截取不同时间间隔的波浪数据,采用统计和相关分析…...

hudi系列-数据写入方式及使用场景
hudi支持多种数据写入方式:insert、bulk_insert、upsert、boostrap,我们可以根据数据本身属性(append-only或upsert)来选择insert和upsert方式,同时也支持对历史数据的高效同步并嫁接到实时流程。 这里的使用技术组合为flink + hudi-0.11 upsert 这是hudi默认的写入方式,…...

C # FileStream文件流
本章讲述:FileStream类的基本功能,以及简单示例; 1、引用命名空间:using System.IO; 2、注意:使用IO操作文件时,要注意流关闭和释放问题! 强力推荐:将创建文件流对象的过程写在usi…...
Go语言中的保留字和运算符详解
前言 🏠个人主页:我是沐风晓月 🧑个人简介:大家好,我是沐风晓月,双一流院校计算机专业,阿里云博客专家 😉😉 💕 座右铭: 先努力成长自己ÿ…...
C语言基础)
Linux编译之(1)C语言基础
Linux编译之C语言基础 Author:Once Day Date:2023年3月11日 漫漫长路,才刚刚开始… 1.概述 在Linux下开发多源文件的C代码文件,是一定要了解Makefile的,虽然现在构建工具很多,但学习的一开始࿰…...
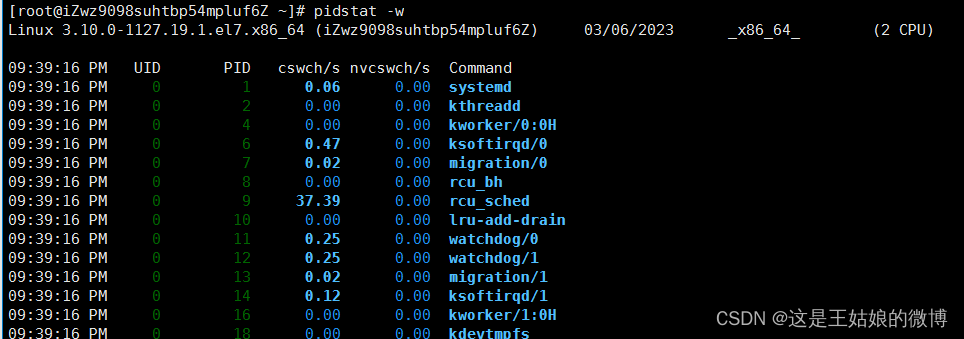
CPU平均负载高问题定位分析
一、Linux操作系统CPU平均负载 1.1什么是CPU平均负载 1.2 怎么查看平均负载数值 二、Linux操作系统CPU使用率和平均负载区别 CPU使用率和平均负载区别 三、阿里云Linux操作系统CPU压测环境准备 3.1 核心命令应用场景 3.2 模拟生产环境出现的多种问题环境准备 分析工具安…...

Python蓝桥杯训练:基本数据结构 [二叉树] 中
Python蓝桥杯训练:基本数据结构 [二叉树] 中 文章目录Python蓝桥杯训练:基本数据结构 [二叉树] 中一、[翻转二叉树](https://leetcode.cn/problems/invert-binary-tree/)二、[对称二叉树](https://leetcode.cn/problems/symmetric-tree/)三、[二叉树的最…...
 – UDS 协议)
读取 DTC 信息服务 (0x19) – UDS 协议
总目录链接>> AutoSAR入门和实战系列总目录 0x19读取 DTC 信息服务概述 读取 DTC 信息服务在 UDS 协议中用于从车辆或特定 ECU 或节点读取 DTC。UDS 协议的主要任务之一是故障诊断。每当车辆发生任何故障时,与该故障相对应的诊断故障代码(DTC&a…...

Hive 分区表新增字段 cascade
背景 在以前上线的分区表中新加一个字段,并且要求添加到指定的位置列。 模拟测试 加 cascade 操作 创建测试表 create table if not exists sqltest.table_add_column_test(org_col1 string comment 原始数据1,org_col2 string comment 原始数据2 ) comment 增…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
