机器学习中的数学原理——模型评估与交叉验证
惭愧惭愧!机器学习中的数学原理这个专栏已经很久没有更新了!前段时间一直在学习深度学习,paddlepaddle,刷题专栏跟新了,这个专栏就被打入冷宫了。这个专栏名为白话机器学习中数学学习笔记,主要是用来分享一下我在 机器学习中的学习笔记及一些感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎私信或者评论区留言!这一篇就更新一下《 白话机器学习中的数学——模型评估与交叉验证》!
文章目录
- 一、什么是模型评估
- 二、交叉验证
- 2.1回归问题的交叉验证
- 2.2分类问题的验证
一、什么是模型评估
简单的讲,模型评估就是评估训练好的模型的好坏。
在进行回归和分类时,为了进行预测,我们定义了函数 fθ(x),然后根据训练数据求出了函数的参数 θ。也就是对目标函数进行微分,然后求出参数更新表达式的操作,当时我们求出参数更新表达式之后就结束了。
但是,其实我们真正想要的是通过预测函数得到预测值。以回归的那个例子来说,就是关于投入的广告费能带来多少点击量的预测值。所以我们希望 fθ(x)对未知数据 x 输出的预测值尽可能正确。那我们如何测量预测函数 fθ(x)的正确性,也就是精度呢?对于一个变量的问题,我可以用图直观的表示出来:
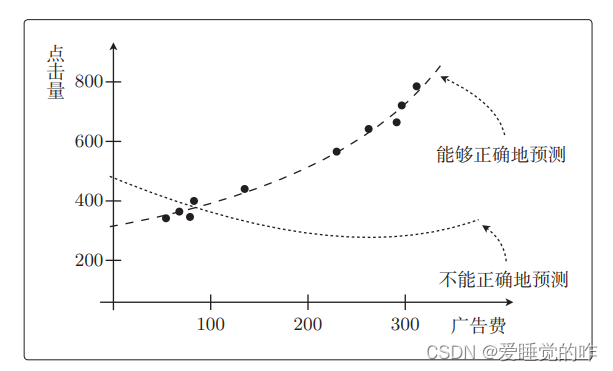
二、交叉验证
验证是指的在机器学习模型训练时对模型好坏程度的衡量。交叉验证就是一种常用的模型选择方法,使用部分数据集进行验证模型的有效性。
2.1回归问题的交叉验证
把获取的全部训练数据分成两份:一份用于测试,一份用于训练。然后用前者来评估模型。也就是说假如有 10 个训练数据,那么实际上会按照 5 个测试数据、5 个训练数据来分配它们,但是比起 5 : 5,大多数情况会采用 3 : 7 或者 2 : 8 这种训练数据更多的比例。
我们接下来用3 个用于测试、7 个用于训练。也就是说,关于点击量预测的回归问题,我们现在有 10 个数据,其中测试数据和训练数据是这样分配的:
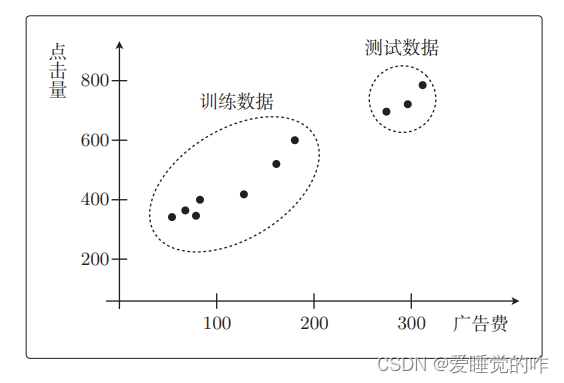
fθ(x)=θ0+θ1x∗f_{\boldsymbol{\theta}}(\boldsymbol{x})=\theta_0+\theta_1 x^*fθ(x)=θ0+θ1x∗表示即可。先从一次函数开始考虑比较好。先不去管测试数据,只看那7个训练数据。一次拟合函数大概如下:
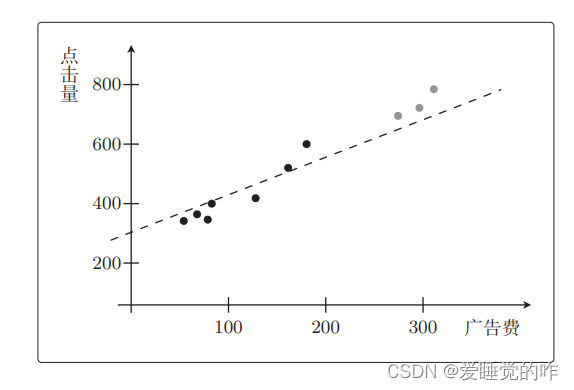
再考虑二次函数:
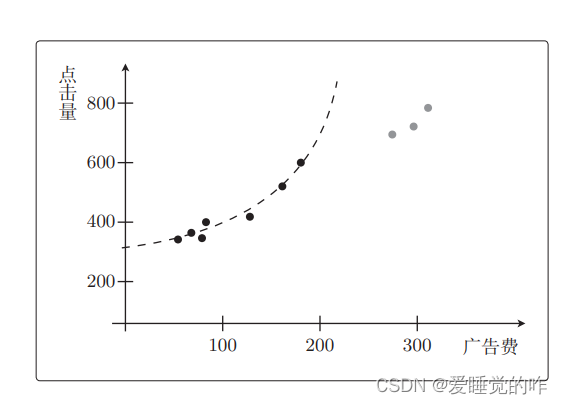
但是,如果将测试数据也考虑进来,那么二次函数就完全不行了。要把测试数据当作未知数据来考虑。即使模型相同,如果训练数据过少,这种现象也会发生。那么在训练结束之后,我们还得像这样检查一下测试数据是否也拟合,但是如果变量增加,就不能画图了。就算能画图,也会很麻烦。
对于回归的情况,只要在训练好的模型上计算测试数据的误差的平方,再取其平均值就可以了。假设测试数据有 n 个,那么可以这样计算。
1n∑i=1n(y(i)−fθ(x(i)))2\frac{1}{n} \sum_{i=1}^n\left(y^{(i)}-f_{\boldsymbol{\theta}}\left(\boldsymbol{x}^{(i)}\right)\right)^2n1∑i=1n(y(i)−fθ(x(i)))2
对于预测点击量的回归问题来说,y(i) 就是点击量,而 x(i) 是广告费或广告版面的大小,这个值被称为均方误差或者 MSE,全称 Mean Square Error。这个误差越小,精度就越高,模型也就越好。
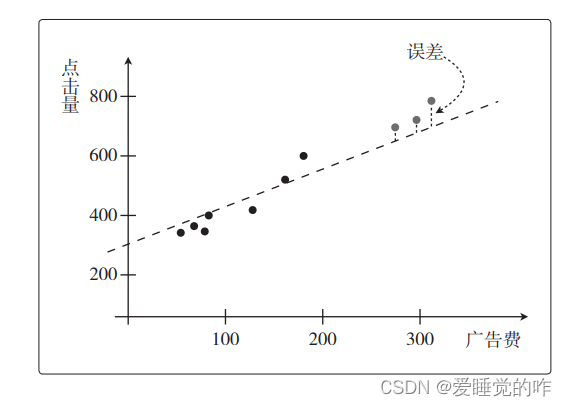
回归的目标函数也是误差函数,这与为了让误差函数的值变小而更新参数时所做的事情是一样的!
2.2分类问题的验证
与回归的时候一样,我们先考虑数据的分配。
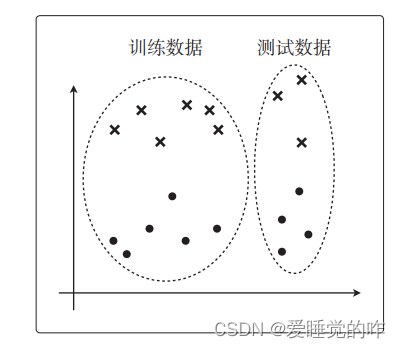
数据的分配方法不要太极端其实会更好”这一点与回归的时候也是一样的。假设在逻辑回归的情况下,θTx 是简单的一次函数,那么只根据训练数据进行训练后,决策边界应该是这样的:
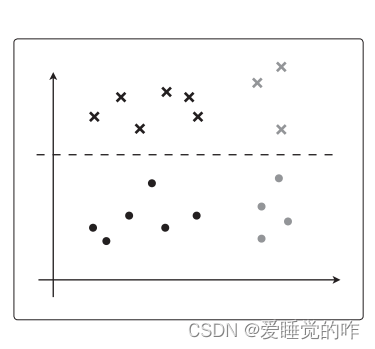
但是假如θTx 更加复杂,可能就会像这样紧贴着训练数据进行分类:
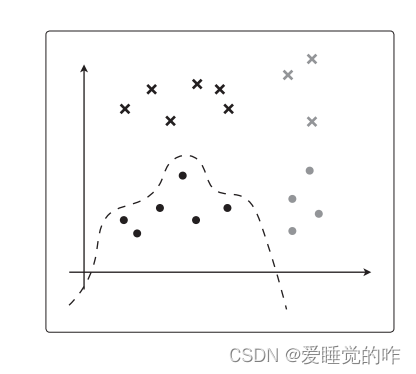
可以看到可以对训练数据完美地进行分类,却完全忽视了测试数据。对于分类有别的指标。由于回归是连续值,所以可以从误差入手,但是在分类中我们必须要考虑分类的类别是否正确。在回归中要考虑的是答案不完全一致时的误差,而分类中要考虑的是答案是否正确。
我们对图像是横向的还是纵向的进行了分类,我们是根据图像为横向的概率来分类的。关于分类是否成功就会有下面 4 种情况:
- 图像是横向的,被正确分类了
- 图像被分类为横向,但实际上不是横向的
- 图像不是横向的,被正确分类了
- 图像被分类为非横向,但实际上是横向的
把它整理到这样的表里:
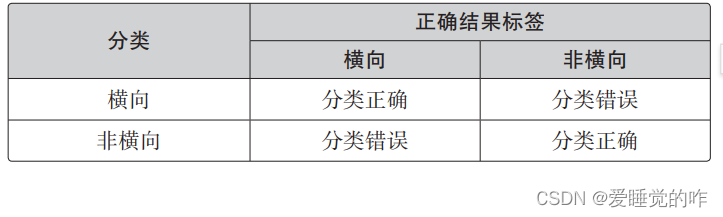
设横向的情况为正、非横向的情况为负,那么一般来说,二分类的结果可以用这张表来表示:
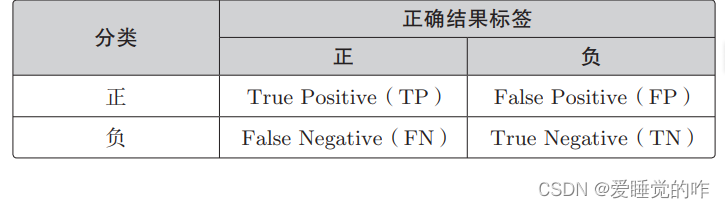
分类结果为正的情况是 Positive、为负的情况是 Negative。分类成功为 True、分类失败为 False。我们可以使用表里的 4 个记号来计算分类的精度。精度的英文是 Accuracy,它的计算表达式是这样的:
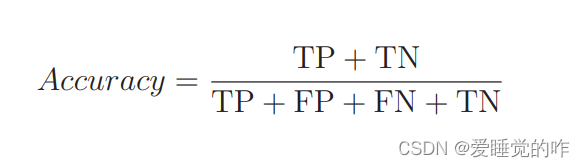
它表示的是在整个数据集中,被正确分类的数据 TP 和 TN 所占的比例。假如 100 个数据中 80 个被正确地分类了,那么精度就是这样的:
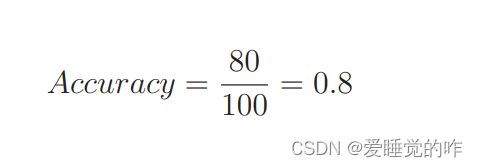
用测试数据来计算这个值,值越高精度越高,也就意味着模型越好!
相关文章:
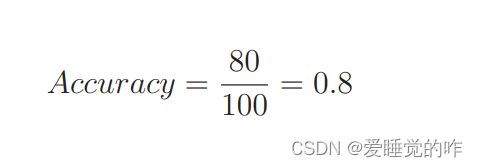
机器学习中的数学原理——模型评估与交叉验证
惭愧惭愧!机器学习中的数学原理这个专栏已经很久没有更新了!前段时间一直在学习深度学习,paddlepaddle,刷题专栏跟新了,这个专栏就被打入冷宫了。这个专栏名为白话机器学习中数学学习笔记,主要是用来分享一…...
JAVA开发(JSP的9大内置对象和4大作用域)
背景: 在springboot横行的javaweb开发中,现在的后端开发工程师基本不需要写前端JSP页面。但是作为web开发工程师,不懂JSP的原理和作用,几乎是不行的。 JSP技术介绍: JSP(全称Java Server Pagesÿ…...
EKF失控保护)
(4)EKF失控保护
文章目录 前言 4.1 什么时候会触发? 4.2 当失控保护触发时,会发生什么?...
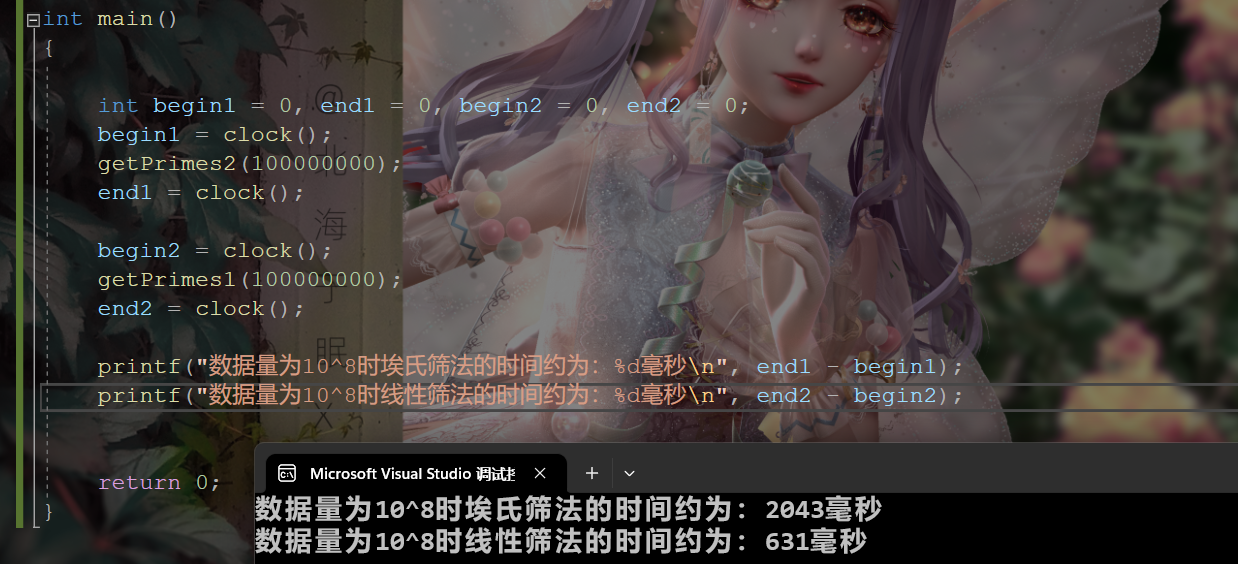
数论----质数的求解(C/C++)
CSDN的uu,你们好呀,今天我们要学习的内容是数论哦!这也是算法题中的一类题目吧。记好安全带,准备发车咯!🚀学习数论的意义📢算法导论说:“数论曾经被视为一种虽然优美但却没什么用处…...
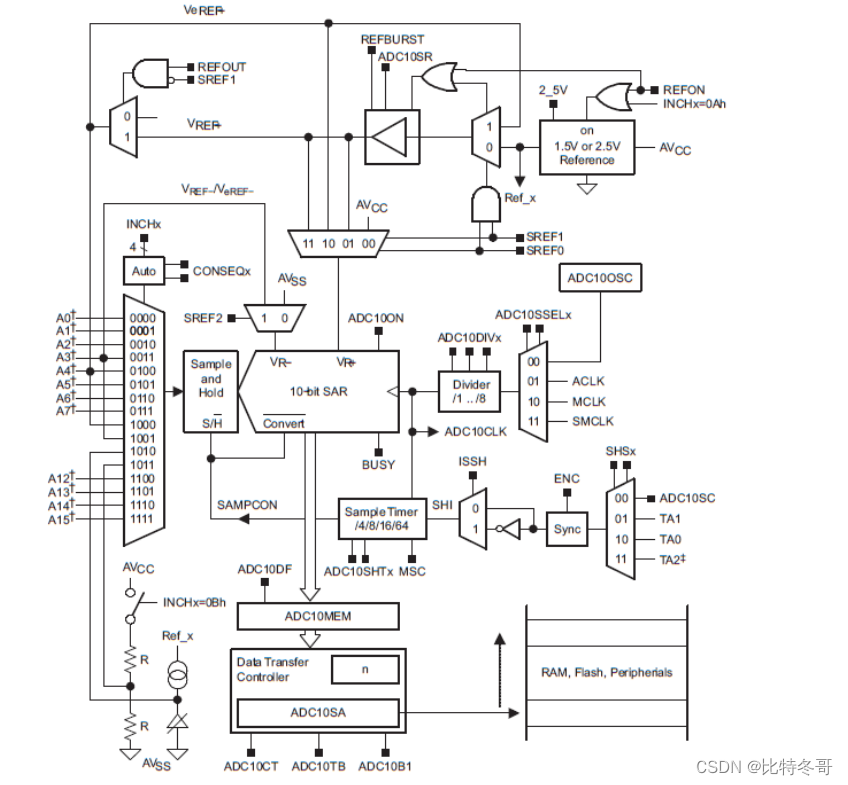
【电赛MSP430系列】GPIO、LED、按键、时钟、中断、串口、定时器、PWM、ADC
文章目录MSP430一、GPIO二、点亮LED三、按键控制LED四、更改主时钟五、串口通信六、串口中断七、外部中断八、定时器九、定时器中断十、PWM十一、ADCMSP430 MSP430 是德州仪器(TI)一款性能卓越的超低功耗 16 位单片机,自问世以来,…...

【Linux】进程理解与学习(Ⅱ)
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹相关文章推荐:【Linux】冯.诺依曼体系结构与操作系统【Linux】进程理解与学习(Ⅰ)浅谈Linux下的shell--BASH前言章节…...

vscode 爽到起飞的快捷键
这里写目录标题1. 窗口操作2. 代码编辑3. 批量操作4. 错误处理1. 窗口操作 文件之间切换: CtrlTab 切出一个新的编辑器窗口(最多3个): Ctrl\ 切换左中右3个编辑器窗口的快捷键: Ctrl1 Ctrl2 Ctrl3 2. 代码编辑 代码格式化: ShiftAltF 向上或向下移动一行: Alt…...
vs +qt 打包.cpp和.h为DLL文件
文章目录一 编译成库1 创建一个Qt library 项目2,将已有的文件拷贝到项目目录下3 在项目中添加现有项4,拷贝头文件到需要暴露给外面使用的类的头文件中5 拷贝xxx_EXPORT的宏到需要被暴露的类的名前面6 然后点击编译 就完成了。得到的dll文件在debug里面二…...

echarts有滑块
vue下使用echarts折线图及其横坐标拖拽功能 drawLine() {let that this,lineDate [],dispatchCount [],finishCount [],newCount [];let param {// 参数};axios.post(url, param).then(function(response) {let rs response.data.data;if (rs ! undefined && rs…...

MATLAB绘制ROC曲线
ROC曲线(Receiver Operating Characteristic Curve) 1 简介 ROC曲线是用于评估二元分类模型(如Logistic回归)表现优劣的一种工具,其横轴表示假阳性率(false positive rate,FPR),即实际为负例但…...
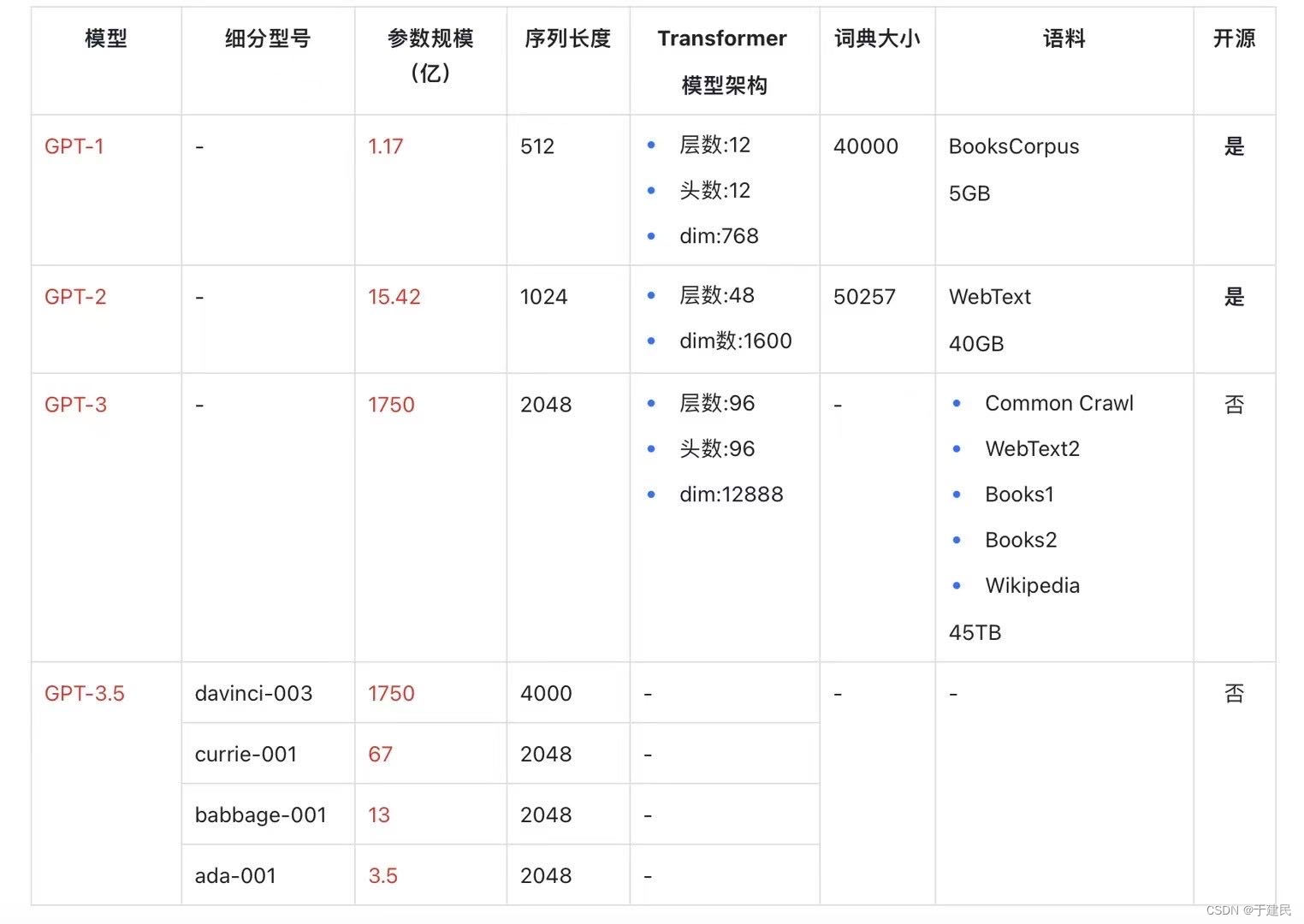
ChatGPT前传
文章目录前言GPT概述GPT-1代GPT-1 学习目标和概念介绍GPT-1 训练数据集GPT-1 模型结构和应用细节GPT-1 效果性能和总结GPT-2代GPT-2 学习目标和概念介绍GPT-2 训练数据集GPT-2 模型结构和应用细节GPT-2 性能效果和总结GPT-3代GPT-3 学习目标和概念介绍GPT-3 训练数据集GPT-3 模…...

我的十年编程路 2020年篇
我出生在1990年,2020年到来的时候,我完成了一项成就:奔三。同时,也开启了新的征程:奔四。 2020年的春节是在广州的丈母娘家度过的,春节后大概是初五,或者是初六,我和媳妇就返回天津…...

力扣-SQL【入门】
https://leetcode.cn/study-plan/sql/?progressxhqm4sjh 目录选择595. 大的国家1757. 可回收且低脂的产品584. 寻找用户推荐人183. 从不订购的客户排序 & 修改1873. 计算特殊奖金627. 变更性别196. 删除重复的电子邮箱选择 595. 大的国家 # Write your MySQL query state…...
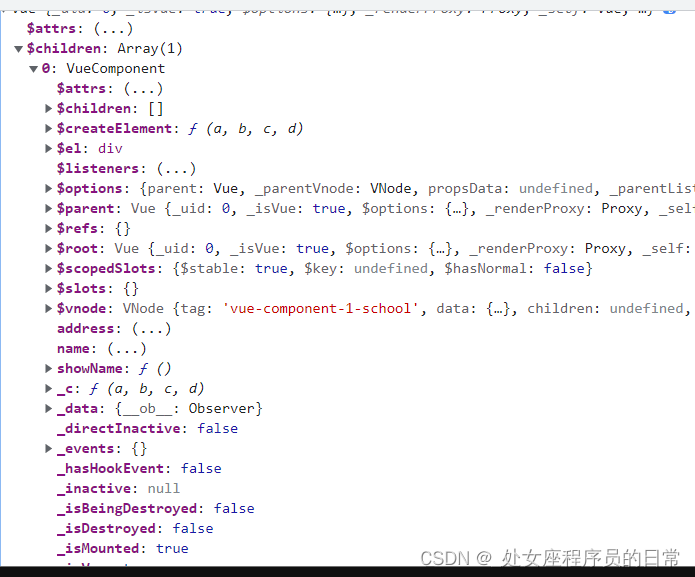
Vue中组件到底是什么
1.先说结论: Vue中组件本质是一个名为VueComponent的构造函数,且不是程序员定义的,是Vue.extend生成的。 2.我们使用组件时发生了什么? 比如定义了一个school,然后在页面上使用它 我们只需要写 < school/ > 或< school &…...

不同时间间隔数据对统计结果的影响
目录摘要1. 实测数据来源2. 数据分析方法3 结果分析3.1 波况分析摘要 采用不同的波浪观测方法所获得的波浪数据的时间间隔不一致,其数据的准确性须进行分析。基于大埕湾逐时周年波浪观测数据,截取不同时间间隔的波浪数据,采用统计和相关分析…...

hudi系列-数据写入方式及使用场景
hudi支持多种数据写入方式:insert、bulk_insert、upsert、boostrap,我们可以根据数据本身属性(append-only或upsert)来选择insert和upsert方式,同时也支持对历史数据的高效同步并嫁接到实时流程。 这里的使用技术组合为flink + hudi-0.11 upsert 这是hudi默认的写入方式,…...

C # FileStream文件流
本章讲述:FileStream类的基本功能,以及简单示例; 1、引用命名空间:using System.IO; 2、注意:使用IO操作文件时,要注意流关闭和释放问题! 强力推荐:将创建文件流对象的过程写在usi…...
Go语言中的保留字和运算符详解
前言 🏠个人主页:我是沐风晓月 🧑个人简介:大家好,我是沐风晓月,双一流院校计算机专业,阿里云博客专家 😉😉 💕 座右铭: 先努力成长自己ÿ…...
C语言基础)
Linux编译之(1)C语言基础
Linux编译之C语言基础 Author:Once Day Date:2023年3月11日 漫漫长路,才刚刚开始… 1.概述 在Linux下开发多源文件的C代码文件,是一定要了解Makefile的,虽然现在构建工具很多,但学习的一开始࿰…...
CPU平均负载高问题定位分析
一、Linux操作系统CPU平均负载 1.1什么是CPU平均负载 1.2 怎么查看平均负载数值 二、Linux操作系统CPU使用率和平均负载区别 CPU使用率和平均负载区别 三、阿里云Linux操作系统CPU压测环境准备 3.1 核心命令应用场景 3.2 模拟生产环境出现的多种问题环境准备 分析工具安…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
