为什么KV Cache只需缓存K矩阵和V矩阵,无需缓存Q矩阵?
大家都知道大模型是通过语言序列预测下一个词的概率。假定{ x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,…, x n − 1 x_{n-1} xn−1}为已知序列,其中 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,…, x n − 1 x_{n-1} xn−1均为维度是 d m o d e l d_{model} dmodel的向量, q n q_{n} qn、 k n k_{n} kn、 v n v_{n} vn同为向量。当输入 x n x_n xn时,需要预测 x n + 1 x_{n+1} xn+1的概率分布。
KV Cache干了什么?
Attention机制的目标是输入 x n x_n xn,输出 z n z_n zn。在具体实现过程中,输入 x n x_n xn,生成 q n q_n qn、 k n k_n kn和 v n v_n vn,并在实际计算中不再需要重复计算 k 1 k_1 k1, k 2 k_2 k2,…, k n − 1 k_{n-1} kn−1和 v 1 v_1 v1, v 2 v_2 v2,…, v n − 1 v_{n-1} vn−1,直接从缓存中取即可。
具体Attention机制计算流程如下图所示。
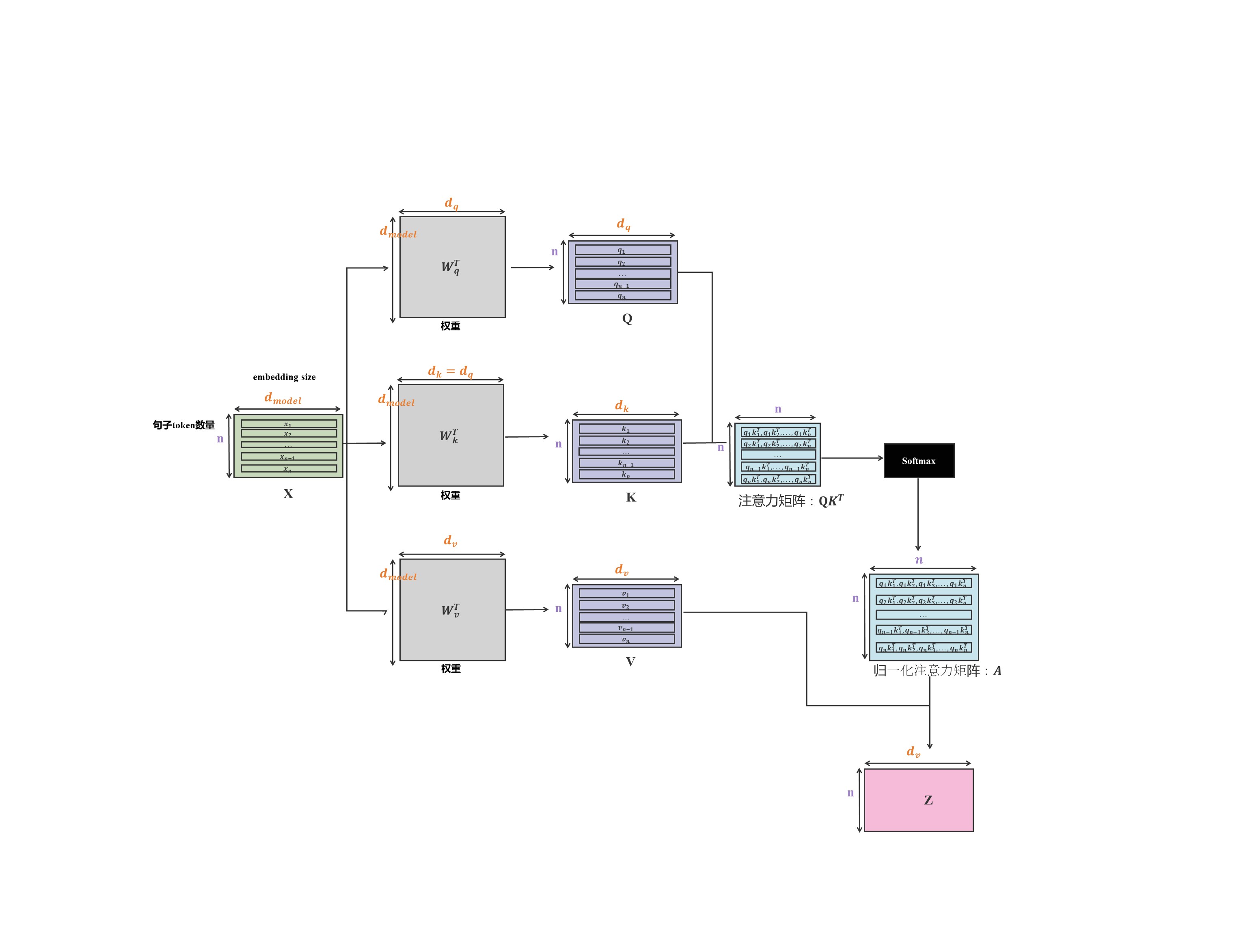
观察注意力矩阵最下面一行(放大图我放下面了)。新输入的 x n x_n xn通过矩阵 W q W_q Wq生成 q n q_n qn,其中 q n q_n qn与 k 1 k_1 k1, k 2 k_2 k2,…, k n k_n kn均有运算关系。所以可以通过缓存 k 1 k_1 k1, k 2 k_2 k2,…, k n − 1 k_{n-1} kn−1向量加速推理。这是K矩阵需要缓存的原因。
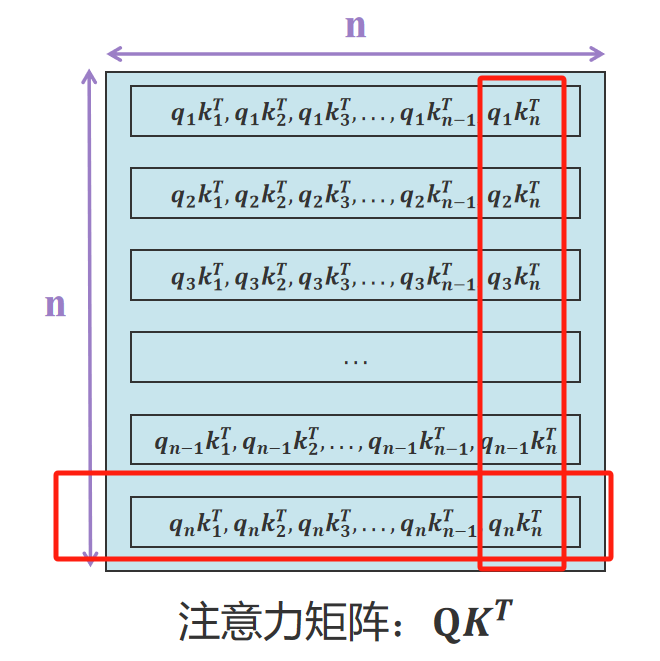
不过很意外的发现最右边一列 q 1 q_1 q1, q 2 q_2 q2,…, q n − 1 q_{n-1} qn−1与 k n k_{n} kn之间存在计算。
不是说好的只有KV缓存,没有Q矩阵缓存?如果推导成立,新输入 x n x_{n} xn是否会改变 x 1 x_1 x1, x 2 x_2 x2,…, x n − 1 x_{n-1} xn−1的注意力分布?
推导没有错,也没有Q矩阵缓存。因为在推理阶段,Attention机制有一个非常重要的细节:mask掩码
注意力矩阵在训练推理过程中,为了模拟真实推理场景,当前位置token是看不到下一位置的,且只能看到上一位置以及前面序列的信息,所以在训练推理的时候加了attention mask。具体实现如下图所示:
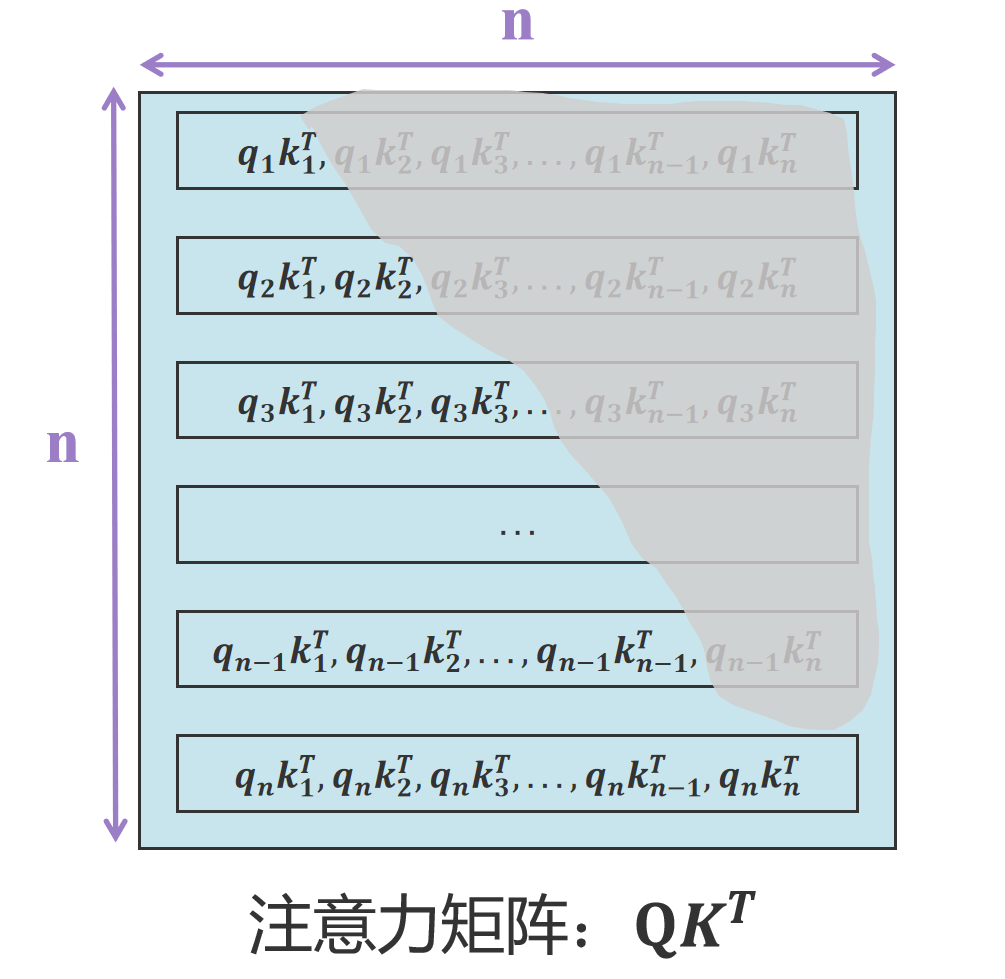
将上图灰色区域全部重置为-inf(负无穷大) ,这样方便softmax的时候置为0。当新输入 x n x_n xn,注意力的计算(见注意力矩阵最下面一行)与 q 1 q_1 q1, q 2 q_2 q2,…, q n − 1 q_{n-1} qn−1无关,因此无需缓存Q矩阵
另外,还有个V矩阵,参照图1就干了一件事。
z n = a 1 ∗ v 1 + a 2 ∗ v 2 + . . . + a n ∗ v n z_n = a1*v_1+a2*v_2+...+a_n*v_n zn=a1∗v1+a2∗v2+...+an∗vn
我可以提前缓存 v 1 v_1 v1, v 2 v_2 v2,…, v n − 1 v_{n-1} vn−1,计算的时候从缓存中取即可,这是V矩阵需要缓存的原因。
相关文章:

为什么KV Cache只需缓存K矩阵和V矩阵,无需缓存Q矩阵?
大家都知道大模型是通过语言序列预测下一个词的概率。假定{ x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,…, x n − 1 x_{n-1} xn−1}为已知序列,其中 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x…...

VS code修改底部的行号的状态栏颜色
VSCode截图 相信很多小伙伴被底部的蓝色状态栏困扰很久了 处理的方式有两种: 1、隐藏状态栏 2、修改其背景颜色 第一种方法大伙都会,今天就使用第二种方法。 1、点击齿轮进入setting 2、我现在用的新版本,设置不是以前那种json格式展示&…...

【鸿蒙学习笔记】MVVM模式
官方文档:MVVM模式 [Q&A] 什么是MVVM ArkUI采取MVVM Model View ViewModel模式。 Model层:存储数据和相关逻辑的模型。View层:在ArkUI中通常是Component装饰组件渲染的UI。ViewModel层:在ArkUI中,ViewModel是…...

端、边、云三级算力网络
目录 端、边、云三级算力网络 NPU Arm架构 OpenStack kubernetes k3s轻量级Kubernetes kubernetes和docker区别 DCI(Data Center Interconnect) SD/WAN TF 端、边、云三级算力网络 算力网络从传统云网融合的角度出发,结合 边缘计算、网络云化以及智能控制的优势,通…...

java —— JSP 技术
一、JSP (一)前言 1、.jsp 与 .html 一样属于前端内容,创建在 WebContent 之下; 2、嵌套的 java 语句放置在<% %>里面; 3、嵌套 java 语句的三种语法: ① 脚本:<% java 代码 %>…...

【Python学习笔记】菜鸟教程Scrapy案例 + B站amazon案例视频
背景前摇(省流可以跳过这部分) 实习的时候厚脸皮请教了一位办公室负责做爬虫这块的老师,给我推荐了Scrapy框架。 我之前学过一些爬虫基础,但是用的是比较常见的BeautifulSoup和Request,于是得到Scrapy这个关键词后&am…...
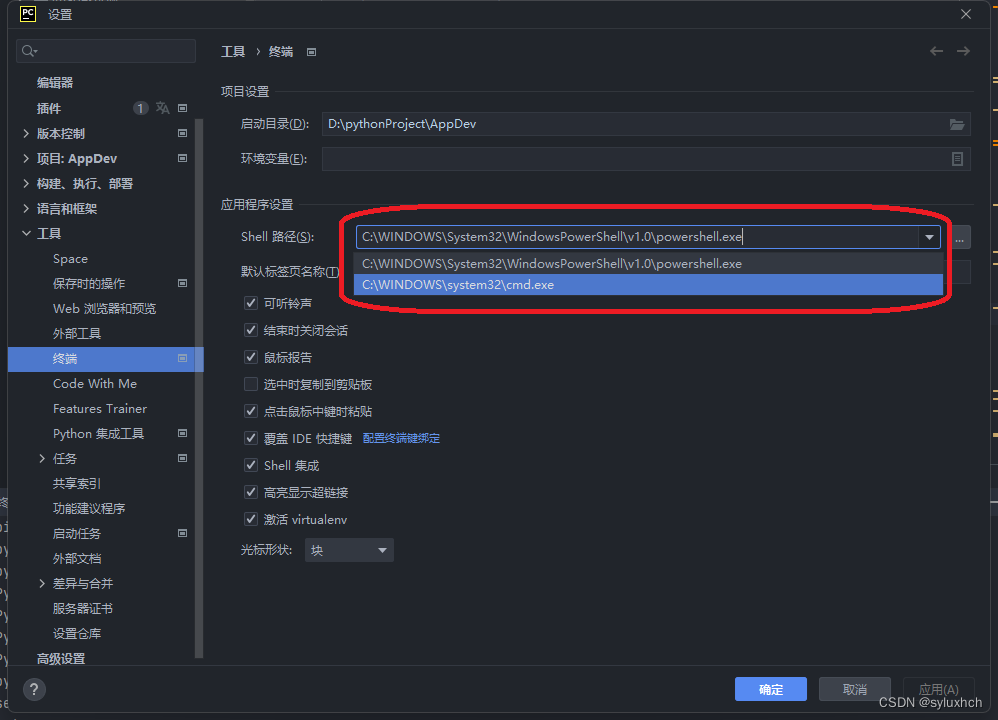
Pycharm的终端(Terminal)中切换到当前项目所在的虚拟环境
1.在Pycharm最下端点击终端/Terminal, 2.点击终端窗口最上端最右边的∨, 3.点击Command Prompt,切换环境, 可以看到现在环境已经由默认的PS(Window PowerShell)切换为项目所使用的虚拟环境。 4.更近一步,如果想让Pycharm默认显示…...

Nginx 高效加速策略:动静分离与缓存详解
在现代Web开发中,网站性能是衡量用户体验的关键指标之一。Nginx,以其出色的性能和灵活性,成为众多网站架构中不可或缺的一部分。本文将深度解析如何利用Nginx实现动静分离与缓存,从而大幅提升网站加载速度和响应效率。 理解动静分…...

Unity3D 游戏摇杆的制作与实现详解
在Unity3D游戏开发中,摇杆是一种非常常见的输入方式,特别适用于移动设备的游戏控制。本文将详细介绍如何在Unity3D中制作和实现一个虚拟摇杆,包括技术详解和代码实现。 对惹,这里有一个游戏开发交流小组,大家可以点击…...

从nginx返回404来看http1.0和http1.1的区别
序言 什么样的人可以称之为有智慧的人呢?如果下一个定义,你会如何来定义? 所谓智慧,就是能区分自己能改变的部分,自己无法改变的部分,努力去做自己能改变的,而不要天天想着那些无法改变的东西&a…...
MySQL 代理层:ProxySQL
文章目录 说明安装部署1.1 yum 安装1.2 启停管理1.3 查询版本1.4 Admin 管理接口 入门体验功能介绍3.1 多层次配置系统 读写分离将实例接入到代理服务定义主机组之间的复制关系配置路由规则事务读的配置延迟阈值和请求转发 ProxySQL 核心表mysql_usersmysql_serversmysql_repli…...

异步主从复制
主从复制的概念 主从复制是一种在数据库系统中常用的数据备份和读取扩展技术,通过将一个数据库服务器(主服务器)上的数据变更自动同步到一个或多个数据库服务器(从服务器)上,以此来实现数据的冗余备份、读…...

论文解析——Full Stack Optimization of Transformer Inference: a Survey
作者及发刊详情 摘要 正文 主要工作贡献 这篇文章的贡献主要有两部分: 分析Transformer的特征,调查高效transformer推理的方法通过应用方法学展现一个DNN加速器生成器Gemmini的case研究 1)分析和解析Transformer架构的运行时特性和瓶颈…...

selenium处理cookie问题实战
1. cookie获取不完整 需要进入的资损平台(web)首页,才会出现有效的ctoken等信息 1.1. 原因说明 未进入指定页面而获取的 cookie 与进入页面后获取的 cookie 可能会有一些差异,这取决于网站的具体实现和 cookie 的设置方式。 通常情况下,一些…...

(十五)GLM库对矩阵操作
GLM简单使用 glm是一个开源的对矩阵运算的库,下载地址: https://github.com/g-truc/glm/releases 直接包含其头文件即可使用: #include <glad/glad.h>//glad必须在glfw头文件之前包含 #include <GLFW/glfw3.h> #include <io…...

android中activity与fragment之间的各种跳转
我们以音乐播放、视频播放、用户注册与登录为例【Musicfragment(音乐列表页)、Videofragment(视频列表页)、MusicAvtivity(音乐详情页)、VideoFragment(视频详情页)、LoginActivity&…...

动态规划算法-以中学排课管理系统为例
1.动态规划算法介绍 1.算法思路 动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若…...

本安防爆手机:危险环境下的安全通信解决方案
在石油化工、煤矿、天然气等危险环境中,通信安全是保障工作人员生命安全和生产顺利进行的关键。防爆智能手机作为专为这些环境设计的通信工具,提供了全方位的安全通信解决方案。 防爆设计与材料: 防爆智能手机采用特殊的防爆结构和材料&…...

算法学习笔记(8)-动态规划基础篇
目录 基础内容: 动态规划: 动态规划理解的问题引入: 解析:(暴力回溯) 代码示例: 暴力搜索: Dfs代码示例:(搜索) 暴力递归产生的递归树&…...
)
数据库常见问题(持续更新)
数据库常见问题(持续更新) 1、数据库范式? 1NF:不可分割2NF:没有非主属性对候选码存在部分依赖3NF:没有非主属性传递依赖候选码BCNF:消除了主属性对对候选码的传递依赖或部分依赖 2、InnoDB事务的实现? …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
