AdaBoost集成学习算法理论解读以及公式为什么这么设计?
本文致力于阐述AdaBoost基本步骤涉及的每一个公式和公式为什么这么设计。
AdaBoost集成学习算法基本上遵从Boosting集成学习思想,通过不断迭代更新训练样本集的样本权重分布获得一组性能互补的弱学习器,然后通过加权投票等方式将这些弱学习器集成起来得到性能较优的集成模型。
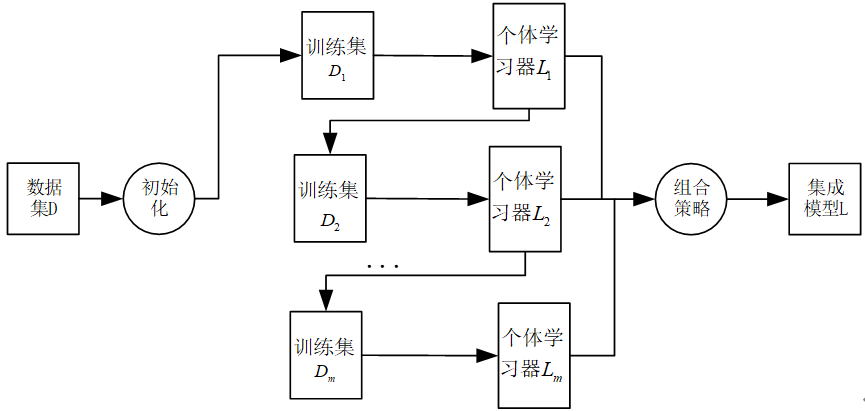
图1:Boosting集成算法思想。
下面以二分类任务(标签不是为-1,就是为+1)为例介绍该算法的具体过程。值得注意的是,下面的公式推导是以二分类任务下得出来,所以公式(比如样本权重更新公式)才会显得比较整洁,但如果换成其他任务,如多分类,那么公式会复杂很多。
对于训练样本集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) D={\left(x_1,y_1\right),\left(x_2,y_2\right),\ldots,(x_n,y_n)} D=(x1,y1),(x2,y2),…,(xn,yn),其中标签 y i ∈ { − 1 , + 1 } y_i\in\left\{-1,+1\right\} yi∈{−1,+1},由AdaBoost集成学习算法构造集成模型的基本步骤如下:
(1)令 i = 1 i=1 i=1并设定弱学习器的数目m。对应第一次迭代,使用均匀分布初始化训练样本集的权重分布,令 n n n维向量 w i \mathbf{w}^i wi表示第 i i i次需更新的样本权重,则有:
w 1 = ( w 11 , w 12 , … , w 1 n ) T = ( 1 n , 1 n , … , 1 n ) T \mathbf{w}^1=\left(w_{11},w_{12},\ldots,w_{1n}\right)^T=\left(\frac{1}{n},\frac{1}{n},\ldots,\frac{1}{n}\right)^T w1=(w11,w12,…,w1n)T=(n1,n1,…,n1)T
(2)使用权重分布为 w i \mathbf{w}^i wi,此时 i = 1 i=1 i=1的训练样本集 D i D_i Di学习得到第 i i i个弱学习器 L i L_i Li;
(3)计算 L i L_i Li在训练样本集 D i D_i Di上的分类错误率 e i e_i ei:
e i = ∑ k = 1 n w i k I ( L i ( X k ) ≠ y k ) e_i=\sum_{k=1}^{n}{w_{ik}I \left(L_i\left(X_k\right)\neq y_k\right) } ei=∑k=1nwikI(Li(Xk)=yk)
(4)确定弱学习器 L i L_i Li的组合权重 α i \alpha_i αi( α i \alpha_i αi在最后得到最终的集成模型上用到)。由于弱学习器 L i L_i Li的权重取值应与其分类性能相关,对于分类错误率 e i e_i ei越小的 L i L_i Li,则其权重 α i \alpha_i αi应该越大,故有:
α i = 1 2 ln 1 − e i e i = 1 2 ln ( 1 e i − 1 ) \alpha_i=\frac{1}{2}\text{ln}\frac{1-e_i}{e_i}=\frac{1}{2}\text{ln}(\frac{1}{e_i}-1) αi=21lnei1−ei=21ln(ei1−1)
可能会有人会为,为什么要这么设计 α i \alpha_i αi?我在下面给出了解释。
(5)(重点)依据弱学习器 L i L_i Li对训练样本集 D i D_i Di的分类错误率 e i e_i ei更新样本权重,样本权重更新公式为:
w i + 1 , j = w i j exp ( − α i y k L i ( x k ) ) Z i w_{i+1,j}=\frac{w_{ij}\exp(-\alpha_iy_kL_i(x_k))}{Z_i} wi+1,j=Ziwijexp(−αiykLi(xk))
其中:
Z i = ∑ k = 1 n w i j exp ( − α i y k L i ( X k ) ) Z_i=\sum_{k=1}^{n}{w_{ij}\exp(-\alpha_iy_kL_i(X_k))} Zi=∑k=1nwijexp(−αiykLi(Xk))
为归一化因子,保证更新后权重向量为概率分布;
对权重更新公式的解释:
回顾开头,这是一个二分类任务,所以若样本 ( x k , y k ) (x_k,y_k) (xk,yk)分类正确,则要不 y k = L i ( x k ) = 1 y_k=L_i(x_k)=1 yk=Li(xk)=1,要不 y k = L i ( x k ) = − 1 y_k=L_i(x_k)=-1 yk=Li(xk)=−1,因此有 y k ∗ L i ( x k ) = 1 y_k*L_i(x_k)=1 yk∗Li(xk)=1**。**若样本 ( x k , y k ) (x_k,y_k) (xk,yk)分类错误,则要不 y k = − 1 , L i ( x k ) = 1 y_k=-1,L_i(x_k)=1 yk=−1,Li(xk)=1,要不 y k = 1 , L i ( x k ) = − 1 y_k=1,L_i(x_k)=-1 yk=1,Li(xk)=−1,因此有 y k ∗ L i ( x k ) = − 1 y_k*L_i(x_k)=-1 yk∗Li(xk)=−1。
因此公式
w i + 1 , j = w i j exp ( − α i y k L i ( x k ) ) Z i w_{i+1,j}=\frac{w_{ij}\exp(-\alpha_iy_kL_i(x_k))}{Z_i} wi+1,j=Ziwijexp(−αiykLi(xk))
可以改写
w i + 1 , j = { w i j Z i exp ( − α i ) , y k = L i ( x k ) w i j Z i exp ( α i ) , y k ≠ L i ( x k ) w_{i+1,j}=\begin{cases} \frac{w_{ij}}{Z_i}\exp(-\alpha_i),y_k=L_i(x_k) \\\frac{w_{ij}}{Z_i}\exp(\alpha_i),y_k\ne L_i(x_k) \end{cases} wi+1,j={Ziwijexp(−αi),yk=Li(xk)Ziwijexp(αi),yk=Li(xk)
这样,对于错误的样本会被放大 1 − e i e i \frac{1-e_i}{e_i} ei1−ei倍,以便在后续弱学习器构造过程得到应有的重视。
为什么是 1 − e i e i \frac{1-e_i}{e_i} ei1−ei倍?
w i + 1 , j , y k ≠ L i ( x k ) w i + 1 , j , y k = L i ( x k ) = w i j Z i exp ( α i ) w i j Z i exp ( − α i ) = exp ( α i ) exp ( − α i ) = e 2 ∗ α i = e 2 ∗ 1 2 ln 1 − e i e i = e ln 1 − e i e i = 1 − e i e i \frac{w_{i+1,j},y_k\ne L_i(x_k)}{w_{i+1,j},y_k=L_i(x_k)}=\frac{\frac{w_{ij}}{Z_i}\exp(\alpha_i)}{\frac{w_{ij}}{Z_i}\exp(-\alpha_i)} =\frac{\exp(\alpha_i)}{\exp(-\alpha_i)}=e^{2*\alpha_i}=e^{2*\frac{1}{2}\text{ln}\frac{1-e_i}{e_i}}=e^{\text{ln}\frac{1-e_i}{e_i}}=\frac{1-e_i}{e_i} wi+1,j,yk=Li(xk)wi+1,j,yk=Li(xk)=Ziwijexp(−αi)Ziwijexp(αi)=exp(−αi)exp(αi)=e2∗αi=e2∗21lnei1−ei=elnei1−ei=ei1−ei
另外 Z i Z_i Zi的作用是归一化,使得 ∑ j = 1 n w i + 1 , j = 1 \sum_{j=1}^{n}{w_{i+1,j}}=1 ∑j=1nwi+1,j=1
(6)若 i < m i<m i<m,则令 i = i + 1 i=i+1 i=i+1并返回步骤(2),否则执行步骤(7);
(7)对于 m m m个弱分类器 L 1 , L 2 , … , L m L_1{,L}_2,\ldots,L_m L1,L2,…,Lm,分别将每个 L i L_i Li按权重 α i \alpha_i αi进行组合:
L = sign ( ∑ i = 1 m α i L i ( X ) ) L=\text{sign}(\sum_{i=1}^{m}{\alpha_iL_i(X)}) L=sign(∑i=1mαiLi(X))
得到并输出所求集成模型 L L L,算法结束。
参考资料:《机器学习及其应用》汪荣贵等编著
相关文章:

AdaBoost集成学习算法理论解读以及公式为什么这么设计?
本文致力于阐述AdaBoost基本步骤涉及的每一个公式和公式为什么这么设计。 AdaBoost集成学习算法基本上遵从Boosting集成学习思想,通过不断迭代更新训练样本集的样本权重分布获得一组性能互补的弱学习器,然后通过加权投票等方式将这些弱学习器集成起来得到…...

uniapp内置组件uni.navigateTo跳转后页面空白问题解决
文章目录 导文空白问题 导文 在h5上跳转正常 但是在小程序里面跳转有问题 无任何报错 页面跳转地址显示正确,但页面内容为空 空白问题 控制台: 问题解决: 方法1: 可能是没有注册的问题,把没注册的页面 注册一下。 方…...

使用树莓派进行python开发,控制电机的参考资料
网站连接:https://www.cnblogs.com/kevenduan?page1 1、简洁的过程步骤, 2、有代码示例, 3、有注意事项,...

protobuf的使用
protobuf:是一种数据格式,独立于平台,独立于语言,是一种二进制格式,可以存储更加复杂的数据结构,比如图,树,结构体,类 作用: 1.持久化:把数据存…...

笔记15:while语句编程练习
练习一: 编写程序,求 2^24^26^2...n^2? -直到累加和大于或等于 10000 为止,输出累加和 -输出累加式中的项数,以及最大的数 n #include<stdio.h> int main() {int sum 0;int i 1;int n 0;while(sum < 10000)//将sum…...

打开excel时弹出stdole32.tlb
问题描述 打开excel时弹出stdole32.tlb 如下图: 解决方法 打开 Microsoft Excel 并收到关于 stdole32.tlb 的错误提示时,通常意味着与 Excel 相关的某个组件或类型库可能已损坏或不兼容。 stdole32.tlb 是一个用于存储自动化对象定义的类型库&#x…...

349. 两个数组的交集
哈喽!大家好,我是奇哥,一位专门给面试官添堵的职业面试员 文章持续更新,可以微信搜索【小奇JAVA面试】第一时间阅读,回复【资料】更有我为大家准备的福利哟! 文章目录 一、题目二、答案三、总结 一、题目 …...

重庆交通大学数学与统计学院携手泰迪智能科技共建的“智能工作室”
2024年7月4日,重庆交通大学数学与统计学院与广东泰迪智能科技股份有限公司携手共建的“智能工作室”授牌仪式在南岸校区阳光会议室举行。此举标志着数统学院与广东泰迪公司校企合作新篇章的开启,也预示着学院在智能科技教育领域的深入探索和实践。 广东…...

Pandas在生物信息学中的应用详解
Pandas在生物信息学中的应用详解 引言 生物信息学作为一门将计算机科学和生物学相结合的跨学科领域,正随着高通量实验技术的飞速发展而日益重要。Pandas,作为Python中一个强大的数据处理库,为生物信息学研究提供了便捷高效的数据处理和分析…...

ByteMD富文本编辑器的vue3配置
Git地址:GitHub - bytedance/bytemd: ByteMD v1 repository 控制面板输入 npm install bytemd/vue-next 下载成功后在src/main.ts中引用 import "bytemd/dist/index.css";引入后保存,下面是一些插件,比如说我用到gmf和hightLight&…...

基于antdesign封装一个react的上传组件
项目中遇到了一个上传的需求,看了一下已有的代码很粗糙,而且是直接引用andt的组件,体验不太好,自己使用FormData对象封装了一个上传组件,仅供参考。 代码如下: /*** FileUploadModal* description - 文件选…...

ARM裸机:一步步点亮LED(汇编)
硬件工作原理及原理图查阅 LED物理特性介绍 LED本身有2个接线点,一个是LED的正极,一个是LED的负极。LED这个硬件的功能就是点亮或者不亮,物理上想要点亮一颗LED只需要给他的正负极上加正电压即可,要熄灭一颗LED只需要去掉电压即可…...

【单链表】05 有一个带头结点的单链表L,设计一个算法使其元素递增有序。
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux算法题上机准备 😘欢迎 ❤️关注 👍点赞 🙌收藏 ✍️留言 题目 有一个带头结点的单链表L,设计一个算法使其元素递增有序。 算法思路 解决办法有很多&…...

C语言入门基础题:奇偶 ASCII 值判断(C语言版)和ASCII码表,什么是ASCII码,它的特点和应用?
1.题目描述: 任意输入一个字符,判断其 ASCII 是否是奇数,若是,输出 YES ,否则,输出 NO例如,字符 A 的 ASCI 值是 65 ,则输出 YES ,若输入字符 B(ASCII 值是 66)ÿ…...
)
Numpy的广播机制(用于自动处理不同形状的数组)
NumPy 广播是一种强大的机制,允许 NumPy 在执行元素级运算时自动处理不同形状的数组。广播的规则使得无需显式地创建匹配形状的数组,直接进行运算,大大简化了代码并提高了效率。 基本概念 广播的基本思想是让较小的数组在需要的维度上进行扩…...
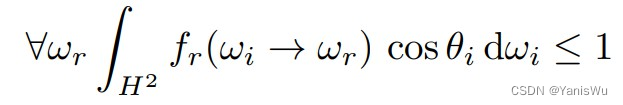
计算机图形学入门24:材质与外观
1.前言 想要得到一个漂亮准确的场景渲染效果,不只需要物理正确的全局照明算法,也要了解现实中各种物体的表面外观和在图形学中的模拟方式。而物体的外观和材质其实就是同一个意思,不同的材质在光照下就会表现出不同的外观,所以外观…...

FTP、http 、tcp
HTTP VS FTP HTTP :HyperText Transfer Protocol 超文本传输协议,是基于TCP协议 FTP: File Transfer Protocol 文件传输协议, 基于TCP协议, 基于UDP协议的FTP 叫做 TFTP HTTP 协议 通过一个SOCKET连接传输依次会话数…...

【虚幻引擎】UE4初学者系列教程开发进阶实战篇——生存游戏案例
一、课程体系 1 学前必读 2 Character类相关基础 -人物移动控制 -动画蓝图 3 常见游戏机制基础 -碰撞器、触发器 -物体使用接口 -视角切换 4其他相关设计 -背包系统 -锻造系统 -物体破碎效果 -简易种植系统 -互动物体动画 5课程结语 二、UI部分 思维导图部分 实操部分 …...

认识并理解webSocket
今天逛牛客,看到有大佬分享说前端面试的时候遇到了关于webSocket的问题,一看自己都没见过这个知识点,赶紧学习一下,在此记录! WebSocket 是一种网络通信协议,提供了全双工通信渠道,即客户端和服…...
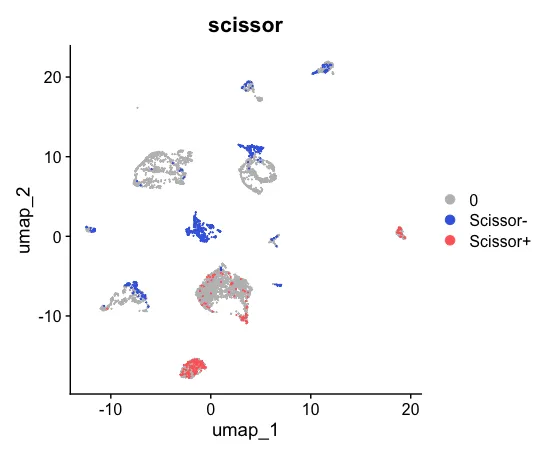
Scissor算法-从含有表型的bulkRNA数据中提取信息进而鉴别单细胞亚群
在做基础实验的时候,研究者都希望能够改变各种条件来进行对比分析,从而探索自己所感兴趣的方向。 在做数据分析的时候也是一样的,我们希望有一个数据集能够附加了很多临床信息/表型,然后二次分析者们就可以进一步挖掘。 然而现实…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
