Linux软件包管理
一、软件包管理
1.什么是软件包
一般在window系统的.exe是软件按转包
2.linux系统下的软件包安装方式
- PRM 软件包安装 软件名称.rpm
- YUM 包管理工具 yum intall 软件名称 -y
- 源码安装 下载源代码---编译---安装 很麻烦,稳定
3.二进制软件包
二进制
4.获取*.rpm 软件包
去官网下载 rpm.phone.net
5.查询系统中安装的rpm软件
rpm -qa | grep 要查询的软件名称
-q:qurey查询
-a:all,代表所有
案例:rpm -qa |grep firefox
6.卸载Centos系统中rpm软件包
rpm -e 软件名称 【选项】
选项说明:
--nodeps:代表强制卸载
7.RPM软件包的安装
8.rpm软件包的升级
9.rpm包常用选项使用
9.1查看已安装的所有软件包
#rpm -qa
#rpm -qa|wc -l
9.2.查看命令(二进制文件)由哪个包安装的
#rpm -qf /usr/sbin/ifconfig
rmp -qf `which ifconfig`
9.3查看已安装的软件包安装了哪些文件
rpm -ql 安装包的名称
9.4删除已安装的软件包
rpm -e 已安装的软件包名
9.5rpm包的依赖关系
9.6rpm包不验依赖关系
rpm -e --nodeps 已安装的包名称
10.源码安装
10.1获取软件的源码包
可以去某个软件的官网获取,一般都是*.tar.gz
网址:https://nginx.org/


10.2源码包安装
- 解压源码包 tar -xvf 包名 -C 指定目录
- 配置 ./configure(配置软件的安装路径,可以不配置,默认使用/usr/local/以软件名称命名的目录)
- 编译make (将软件的源代码编译成类似于rpm包这种可以直接安装的软件)
- 安装 install (把编译好的程序进行安装到linux系统)
10.3使用源码安装nginx
1.安装依赖包
2.下载源代码
3.解压nginx源代码
4.编译安装
5.查看nginx版本,判断软件是否安装成功
11.yum软件包安装
什么是yum
什么是源配置
yum的子配置文件
11.1配置yum源
linux 的yum源有两种,一种是网络yum源需要连接外网才能使用,一种是本地yum源,相当于离线的安装仓库,不需要外网
配置网络yum源
进入案例镜像官网,找到指定网络yum源下载路径,centos7常用两个镜像源,一个epel源,一个centos基本源
阿里云网络yum源地址:https://developer.aliyun.com/mirror/
配置本地yum源
配置yum源需要注意事项
必须配置本地yum仓库
yum的子配置文件必须以.repo结尾的文件(/etc/yum.repos.d)
卸载本地yum源
11.2.yum命令使用
安装软件包
覆盖安装软件包
查看命令由哪个软件包提供的
搜索软件包
删除软件包
11.3yum常用命令
11.4自建yum本地仓库
相关文章:

Linux软件包管理
一、软件包管理 1.什么是软件包 一般在window系统的.exe是软件按转包 2.linux系统下的软件包安装方式 PRM 软件包安装 软件名称.rpmYUM 包管理工具 yum intall 软件名称 -y源码安装 下载源代码---编译---安装 很麻烦,稳定 3.二进制软件包 二进制 4.获取*.rpm…...

如何分辨AI生成的内容?AI生成内容检测工具对比实验
检测人工智能生成的文本对各个领域的组织都提出了挑战,包括学术界和新闻界等。生成式AI与大语言模型根据短描述来进行内容生成的能力,产生了一个问题:这篇文章/内容/作业/图像到底是由人类创作的,还是AI创作的?虽然 LL…...

Clion中怎么切换不同的程序运行
如下图,比如这个文件夹下面有那么多的项目: 那么我想切换不同的项目运行怎么办呢?如果想通过下图的Edit Configurations来设置是不行的: 解决办法: 如下图,选中项目的CMakeLists.txt,右键再点击…...

【C++初阶】C++入门(下)
【C初阶】C入门(下) 🥕个人主页:开敲🍉 🥕所属专栏:C🥭 🌼文章目录🌼 6. 引用 6.1 引用的概念 6.2 引用特性 6.3 常引用 6.4 使用场景 6.5 传值、传引用效率…...

【3】迁移学习模型
【3】迁移学习模型 文章目录 前言一、安装相关模块二、训练代码2.1. 管理预训练模型2.2. 模型训练代码2.3. 可视化结果2.4. 类别函数 总结 前言 主要简述一下训练代码 三叶青图像识别研究简概 一、安装相关模块 #xingyun的笔记本 print(xingyun的笔记本) %pip install d2l %…...

【工具分享】FOFA——网络空间测绘搜索引擎
文章目录 FOFA介绍FOFA语法其他引擎 FOFA介绍 FOFA官网:https://fofa.info/ FOFA(Fingerprinting Organizations with Advanced Tools)是一款网络空间测绘的搜索引擎,它专注于帮助用户收集和分析互联网上的设备和服务信息。FOFA…...

[嵌入式 C 语言] 按位与、或、取反、异或
若协议中如下图所示: 注意: 长度为1,表示1个字节,也就是0xFF,也就是 1111 1111 (这里0xFF只是单纯表示一个数,也可以是其他数,这里需要注意的是1个字节的意思) 一、按位…...

Android --- 运行时Fragment如何获取Activity中的数据,又如何将数据传递到Activity中呢?
1.通过 getActivity() 方法获取 Activity 实例: 在 Fragment 中,可以通过 getActivity() 方法获取当前 Fragment 所依附的 Activity 实例。然后可以调用 Activity 的公共方法或者直接访问 Activity 的字段来获取数据。 // 在 Fragment 中获取 Activity…...
-- Java8 stream的 orElse(null) 和 orElseGet(null))
Java后端开发(十三)-- Java8 stream的 orElse(null) 和 orElseGet(null)
orElse(null)表示如果一个都没找到返回null。【orElse()中可以塞默认值。如果找不到就会返回orElse中你自己设置的默认值。】 orElseGet(null)表示如果一个都没找到返回null。【orElseGet()中可以塞默认值。如果找不到就会返回orElseGet中你自己设置的默认值。】 区别就…...

L2 LangGraph_Components
参考自https://www.deeplearning.ai/short-courses/ai-agents-in-langgraph,以下为代码的实现。 这里用LangGraph把L1的ReAct_Agent实现,可以看出用LangGraph流程化了很多。 LangGraph Components import os from dotenv import load_dotenv, find_do…...

09.C2W4.Word Embeddings with Neural Networks
往期文章请点这里 目录 OverviewBasic Word RepresentationsIntegersOne-hot vectors Word EmbeddingsMeaning as vectorsWord embedding vectors Word embedding processWord Embedding MethodsBasic word embedding methodsAdvanced word embedding methods Continuous Bag-…...
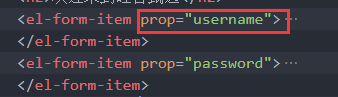
硅谷甄选二(登录)
一、登录路由静态组件 src\views\login\index.vue <template><div class"login_container"><!-- Layout 布局 --><el-row><el-col :span"12" :xs"0"></el-col><el-col :span"12" :xs"2…...

scipy库中,不同应用滤波函数的区别,以及FIR滤波器和IIR滤波器的区别
一、在 Python 中,有多种函数可以用于应用 FIR/IIR 滤波器,每个函数的使用场景和特点各不相同。以下是一些常用的 FIR /IIR滤波器应用函数及其区别: from scipy.signal import lfiltery lfilter(fir_coeff, 1.0, x)from scipy.signal impo…...

简谈设计模式之建造者模式
建造者模式是一种创建型设计模式, 旨在将复杂对象的构建过程与其表示分离, 使同样的构建过程可以构建不同的表示. 建造者模式主要用于以下情况: 需要创建的对象非常复杂: 这个对象由多个部分组成, 且这些部分需要一步步地构建不同的表示: 通过相同的构建过程可以生成不同的表示…...

力扣 hot100 -- 动态规划(下)
目录 💻最长递增子序列 AC 动态规划 AC 动态规划(贪心) 二分 🏠乘积最大子数组 AC 动规 AC 用 0 分割 🐬分割等和子集 AC 二维DP AC 一维DP ⚾最长有效括号 AC 栈 哨兵 💻最长递增子序列 300. 最长递增子序列…...
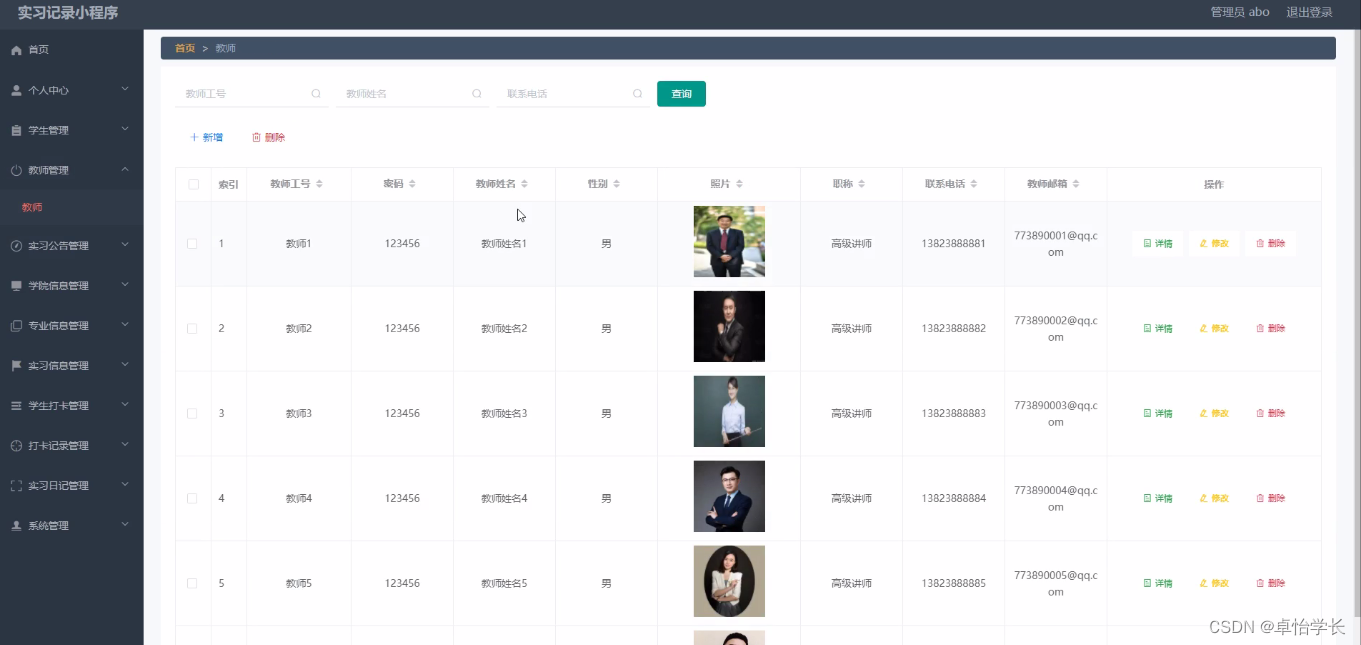
【计算机毕业设计】018基于weixin小程序实习记录
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

力扣之有序链表去重
删除链表中的重复元素,重复元素保留一个 p1 p2 1 -> 1 -> 2 -> 3 -> 3 -> null p1.val p2.val 那么删除 p2,注意 p1 此时保持不变 p1 p2 1 -> 2 -> 3 -> 3 -> null p1.val ! p2.val 那么 p1,p2 向后移动 p1 …...

Apache配置与应用(优化apache)
Apache配置解析(配置优化) Apache链接保持 KeepAlive:决定是否打开连接保持功能,后面接 OFF 表示关闭,接 ON 表示打开 KeepAliveTimeout:表示一次连接多次请求之间的最大间隔时间,即两次请求之间…...
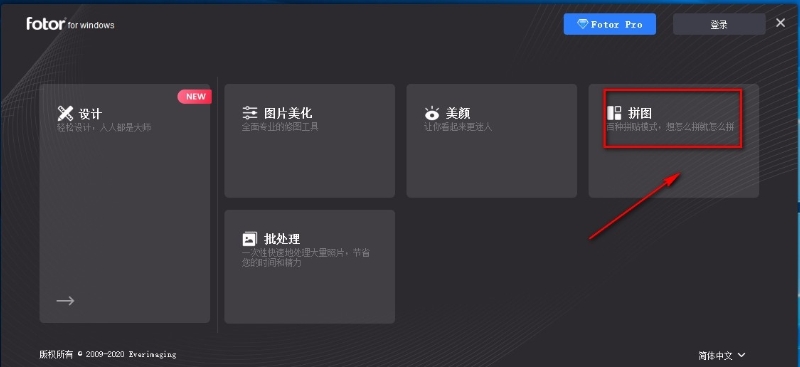
怎么将3张照片合并成一张?这几种拼接方法很实用!
怎么将3张照片合并成一张?在我们丰富多彩的日常生活里,是否总爱捕捉那些稍纵即逝的美好瞬间,将它们定格为一张张珍贵的图片?然而,随着时间的推移,这些满载回忆的宝藏却可能逐渐演变成一项管理挑战ÿ…...
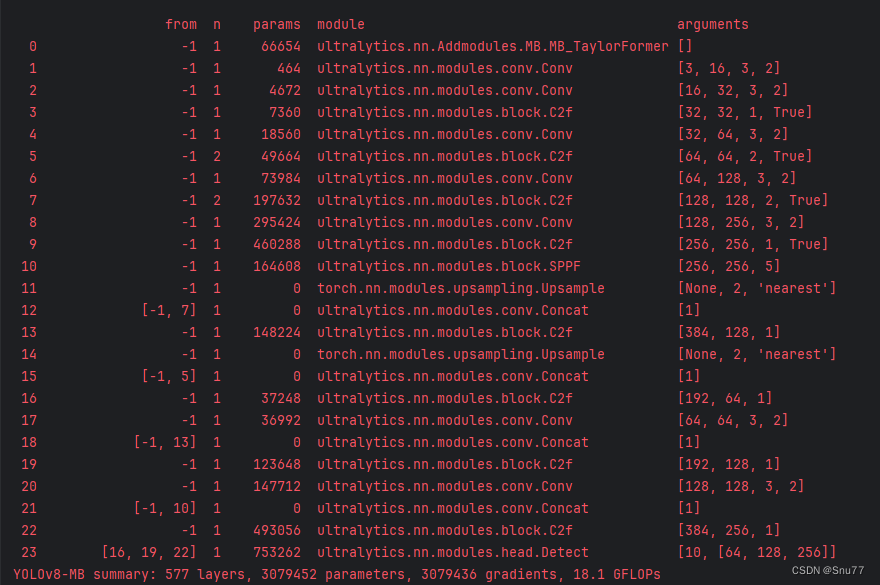
YOLOv10改进 | 图像去雾 | MB-TaylorFormer改善YOLOv10高分辨率和图像去雾检测(ICCV,全网独家首发)
一、本文介绍 本文给大家带来的改进机制是图像去雾MB-TaylorFormer,其发布于2023年的国际计算机视觉会议(ICCV)上,可以算是一遍比较权威的图像去雾网络, MB-TaylorFormer是一种为图像去雾设计的多分支高效Transformer…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
