游戏AI的创造思路-技术基础-决策树(1)
决策树,是每个游戏人必须要掌握的游戏AI构建技术,难度小,速度快,结果直观,本篇将对决策树进行小小解读~~~~

目录
1. 定义
2. 发展历史
3. 决策树的算法公式和函数
3.1. 信息增益(Information Gain)
3.2. 信息增益比(Gain Ratio)
3.3. 基尼指数(Gini Index)
3.4. 三种划分标准对比
4. 运行原理及步骤
5. 优缺点
6. 游戏AI使用决策树算法进行NPC行为控制
6.1. 概述
6.2. 详细过程
6.3. 实例
6.4. Python实现
7. 总述
1. 定义
决策树算法是一种常用的机器学习算法,它通过递归地选择最佳特征来对数据进行分类或回归。
决策树由节点和有向边组成,内部节点表示一个特征或属性,叶节点表示分类或回归的结果。
在游戏AI中,决策树可以帮助NPC更智能地做出决策,提高游戏的趣味性和挑战性。
2. 发展历史
决策树算法的发展可以追溯到1959年,当时的研究人员试图解决人工智能中的决策问题。
1986年,乔治·卢卡斯(George A. Quinlan)提出了ID3算法,这是决策树学习的第一个主要成果。
随后,卢卡斯又提出了C4.5算法,这是ID3算法的改进版本,具有更强的鲁棒性和泛化能力。
CART(Classification and Regression Trees)算法也在此基础上发展,它可以处理连续型特征,适用于回归问题。
3. 决策树的算法公式和函数
决策树算法的核心在于如何选择最优划分特征,通常使用信息增益(Information Gain)、信息增益比(Gain Ratio)或基尼指数(Gini Index)作为划分标准。
3.1. 信息增益(Information Gain)
-
信息增益(Information Gain)公式
其中,是数据集
的信息熵,
是特征
上取值为
的样本子集。
-
Python 实现信息增益
import numpy as np def entropy(y): n = len(y) labels_count = {} for label in y: if label not in labels_count: labels_count[label] = 0 labels_count[label] += 1 ent = 0.0 for label in labels_count: p = labels_count[label] / n ent -= p * np.log2(p) return ent def info_gain(X, y, feature): n = len(y) ent_before = entropy(y) total_gain = 0.0 feature_values = np.unique(X[:, feature]) for value in feature_values: sub_X = X[X[:, feature] == value] sub_y = y[X[:, feature] == value] prob = len(sub_X) / n total_gain += prob * entropy(sub_y) return ent_before - total_gain3.2. 信息增益比(Gain Ratio)
决策树使用信息增益比(Gain Ratio)作为划分标准时,其公式是基于信息增益的,但增加了一个分裂信息(Split Information)的项来规范化信息增益,从而避免偏向于选择取值较多的特征。
- 信息增益比公式
-
信息增益(Information Gain):
-
分裂信息(Split Information):
-
信息增益比(Gain Ratio):
- Python实现代码
以下是使用Python实现信息增益比的代码:
import numpy as np def entropy(y): """计算信息熵""" n = len(y) labels_count = {} for label in y: if label not in labels_count: labels_count[label] = 0 labels_count[label] += 1 ent = 0.0 for label in labels_count: p = labels_count[label] / n ent -= p * np.log2(p) return ent def split_info(X, feature): """计算分裂信息""" n = len(X) feature_values = np.unique(X[:, feature]) split_info = 0.0 for value in feature_values: sub_X = X[X[:, feature] == value] prob = len(sub_X) / n split_info -= prob * np.log2(prob) return split_info def info_gain(X, y, feature): """计算信息增益""" n = len(y) ent_before = entropy(y) total_gain = 0.0 feature_values = np.unique(X[:, feature]) for value in feature_values: sub_X = X[X[:, feature] == value] sub_y = y[X[:, feature] == value] prob = len(sub_X) / n total_gain += prob * entropy(sub_y) return ent_before - total_gain def gain_ratio(X, y, feature): """计算信息增益比""" gain = info_gain(X, y, feature) split_info = split_info(X, feature) if split_info == 0: # 避免除以0的情况 return 0 return gain / split_info # 示例数据
X = np.array([[1, 0], [1, 1], [0, 0], [0, 1]])
y = np.array([0, 0, 1, 1]) # 计算特征0和特征1的信息增益比
print("Gain Ratio for feature 0:", gain_ratio(X, y, 0))
print("Gain Ratio for feature 1:", gain_ratio(X, y, 1))这段代码定义了计算信息熵、分裂信息、信息增益和信息增益比的函数,然后在示例数据上计算了特征0和特征1的信息增益比。
3.3. 基尼指数(Gini Index)
决策树使用基尼指数(Gini index)作为划分标准时,其公式主要用于衡量数据集或数据子集的不纯度。基尼指数越小,表示数据集或数据子集的纯度越高,即选定的特征越好。
- 基尼指数公式
对于给定的数据集 D,其基尼指数 Gini(D) 可以通过以下公式计算:
其中,pk 是数据集 D 中选择第 k 类的概率,J 是类的总数。
对于特征 ,假设它有
个可能的取值 {a1,a2,…,aV},如果使用特征 A 对数据集 D 进行划分,可以得到 V 个子集 {D1,D2,…,DV},其中 Dv 包含所有在特征 A 上取值为 av 的样本。此时,特征 A 对数据集 D 的基尼指数
可以通过以下公式计算:
其中,是子集 Dv 的基尼指数,∣Dv∣ 是子集 Dv 的样本数量,∣D∣ 是数据集 D 的样本总数。
- Python实现代码
以下是使用Python实现基尼指数的代码:
import numpy as np def gini_index(y): """计算数据集的基尼指数""" n = len(y) labels_count = {} for label in y: if label not in labels_count: labels_count[label] = 0 labels_count[label] += 1 gini = 1.0 for label in labels_count: p = labels_count[label] / n gini -= p**2 return gini def gini_index_feature(X, y, feature): """计算特征对数据集的基尼指数""" n = len(y) feature_values = np.unique(X[:, feature]) total_gini = 0.0 for value in feature_values: sub_X = X[X[:, feature] == value] sub_y = y[X[:, feature] == value] prob = len(sub_X) / n total_gini += prob * gini_index(sub_y) return total_gini # 示例数据
X = np.array([[1, 0], [1, 1], [0, 0], [0, 1]])
y = np.array([0, 0, 1, 1]) # 计算特征0和特征1的基尼指数
print("Gini index for feature 0:", gini_index_feature(X, y, 0))
print("Gini index for feature 1:", gini_index_feature(X, y, 1))这段代码定义了计算数据集基尼指数的函数 gini_index。
然后定义了计算特征对数据集基尼指数的函数 gini_index_feature。
最后,在示例数据上计算了特征0和特征1的基尼指数。
3.4. 三种划分标准对比
决策树在构建过程中,选择合适的划分标准至关重要,这直接影响到决策树的性能和效率。信息增益(Information Gain)、信息增益比(Gain Ratio)和基尼指数(Gini Index)是三种常用的划分标准,它们各自具有不同的优点和缺陷。
- 信息增益(Information Gain)
优点:
- 直观易懂:信息增益的计算过程简单明了,易于理解和解释。它反映了使用某个特征进行划分后,数据集纯度的提升程度。
- 适应性强:信息增益可以适应多个类别之间的分类问题,并可以应用于离散型和连续型的特征。
- 多特征值偏好:信息增益在计算时考虑了特征的不确定性程度,因此对于具有更多特征值的特征更有利,这有助于捕捉数据中的细节信息。
缺陷:
- 特征值偏好:信息增益倾向于选择具有更多特征值的特征作为划分特征,这可能导致决策树过于复杂,增加过拟合的风险。
- 忽略相关性:信息增益独立地计算每个特征的重要性,可能忽视了特征之间的相关性,而特征之间的相关性对于分类问题具有重要意义。
- 信息增益比(Gain Ratio)
优点:
- 规范化信息增益:信息增益比通过引入分裂信息(Split Information)对信息增益进行了规范化,从而减少了信息增益对具有更多特征值特征的偏好。
- 处理特征值偏差:在信息增益的基础上,信息增益比更好地处理了特征值分布偏差大的情况,提高了决策树的健壮性。
缺陷:
- 计算复杂度:由于需要计算分裂信息,信息增益比的计算复杂度略高于信息增益,特别是在处理大规模数据集时。
- 可能偏向取值少的特征:在某些情况下,信息增益比可能过于偏向取值数目较少的特征,这需要根据具体数据集进行权衡。
- 基尼指数(Gini Index)
优点:
- 计算效率高:基尼指数的计算方式相对简单,不涉及对数运算,因此在处理大规模数据集时具有较高的效率。
- 不偏向特征值:基尼指数在计算特征重要性时不考虑特征的不确定性程度,因此不会偏向于具有更多特征值的特征。
- 二分类友好:基尼指数特别适用于二分类问题,能够直观地反映分类的准确性。
缺陷:
- 不直观:基尼指数作为一个概率指标,其计算过程相对较为抽象,不如信息增益直观易懂。
- 多分类问题:虽然基尼指数可以应用于多分类问题,但在处理多个类别之间的分类时,其效果可能不如信息增益或信息增益比。
- 小结
三种划分标准各有优缺点,选择哪种标准取决于具体问题的特点和数据集的特征。
在实际应用中,可以通过交叉验证等方法来评估不同划分标准对决策树性能的影响,从而选择最适合的划分标准。
4. 运行原理及步骤
决策树的构建过程包括选择最佳划分特征、递归地划分数据集、剪枝等步骤。
- 步骤
- 选择最佳划分特征:根据信息增益、信息增益比或基尼指数选择最佳划分特征。
- 划分数据集:根据选择的特征和特征值划分数据集。
- 递归构建决策树:对每个子数据集重复上述步骤,直到满足停止条件(如所有样本属于同一类,或没有更多特征等)。
- 剪枝:为了防止过拟合,通常需要对决策树进行剪枝。
- Python 实现决策树构建
class DecisionTree: def __init__(self, max_depth=None, min_samples_split=2): self.max_depth = max_depth self.min_samples_split = min_samples_split self.root = None def fit(self, X, y): self.root = self._build_tree(X, y, 0) def _build_tree(self, X, y, depth): # 停止条件 if depth >= self.max_depth or len(np.unique(y)) == 1 or len(X) < self.min_samples_split: return Node(value=np.argmax(np.bincount(y))) # 选择最佳划分特征 best_feature, best_thresh = self._best_split(X, y) # 划分数据集 left_idxs, right_idxs = self._split(X[:, best_feature], best_thresh) # 递归构建子树 left = self._build_tree(X[left_idxs, :], y[left_idxs], depth + 1) right = self._build_tree(X[right_idxs, :], y[right_idxs], depth + 1) return Node(best_feature, best_thresh, left, right) # 辅助函数:选择最佳划分特征和阈值、划分数据集等5. 优缺点
- 优点
- 易于理解和实现。
- 计算效率高,对于分类问题表现良好。
- 能够处理非线性关系。
- 可以清晰地显示决策过程,便于解释。
- 缺点
- 容易过拟合,需要通过剪枝等技术解决。
- 对缺失值比较敏感,需要额外处理。
- 在某些复杂问题上可能不如神经网络等算法表现优异。
6. 游戏AI使用决策树算法进行NPC行为控制
在游戏开发中,NPC(非玩家角色)的行为控制是一个重要方面。
使用决策树算法可以有效地管理和控制NPC的行为,使其根据游戏环境和玩家行为做出合理的反应。
6.1. 概述
决策树是一种基于树结构的决策模型,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果。
6.2. 详细过程
- 定义行为: 确定NPC可能执行的所有行为,例如攻击、逃跑、对话等。
- 确定属性: 选择影响NPC行为的属性,如玩家距离、玩家状态(攻击、防御等)、NPC当前状态等。
- 构建决策树: 使用属性构建决策节点,每个节点根据属性做出决策,并决定下一步的行为。
- 实施行为: 根据决策树的结果,NPC执行相应的行为。
6.3. 实例
假设我们有一个简单的游戏,NPC可以执行两种行为:攻击和逃跑。我们考虑两个属性:玩家距离和玩家状态。
- 如果玩家距离小于5米且玩家处于攻击状态,NPC选择逃跑。
- 如果玩家距离小于5米且玩家不处于攻击状态,NPC选择对话。
- 如果玩家距离大于等于5米,NPC选择巡逻。
6.4. Python实现
class NPC: def __init__(self, name): self.name = name def decide_action(self, player_distance, player_is_attacking): # 根据玩家距离和玩家状态决定NPC的行为 if player_distance < 5: if player_is_attacking: return "逃跑" else: return "对话" else: return "巡逻" # 实例化NPC
npc = NPC("守卫") # 调用decide_action方法决定NPC的行为,并打印结果
action = npc.decide_action(3, True)
print(f"{npc.name}决定{action}")这段代码定义了一个NPC类,其中__init__方法是构造函数,用于初始化NPC的姓名。
decide_action方法根据传入的玩家距离(player_distance)和玩家是否处于攻击状态(player_is_attacking)来决定NPC应该执行的行为,并返回该行为。
最后,代码创建了一个名为“守卫”的NPC实例,并调用decide_action方法来决定其行为,然后打印出结果。
7. 总述
决策树算法运用于游戏的AI中,历史悠久,难度相对其他算法来说最低,也是运用最广的一种方法。简单的决策树早就在红白机时代就已初见雏形。随着近年来的发展,决策树更多的关注于自动决策树生成,后面有机会会着重于此部分论述。
相关文章:
游戏AI的创造思路-技术基础-决策树(1)
决策树,是每个游戏人必须要掌握的游戏AI构建技术,难度小,速度快,结果直观,本篇将对决策树进行小小解读~~~~ 目录 1. 定义 2. 发展历史 3. 决策树的算法公式和函数 3.1. 信息增益(Information Gain&…...

OPenCV实现直方图均衡化----20240711
# 直方图均衡化import cv2 import numpy as np import matplotlib.pyplot as plt# 读取彩色图像 img = cv2.imread("./pictures/Lena.jpg")# 检查图像是否加载成功 if img is None:print("Could not open or find the i...

2023年全国大学生电子信息竞赛E题——自动追踪系统(stm32和openmv+普通舵机)完美解决第四问
当时做的时候,当时看别人开源的23年的题,感觉一头雾水。两个字没思路。确实只有做了才会有思路。我这里清晰的整理出来思路。 1.第一问的复位问题就是写一个函数,如果按键按下,就进入,再按下就退出 当然这个复位是写死…...
【UNI-APP】阿里NLS一句话听写typescript模块
阿里提供的demo代码都是javascript,自己捏个轮子。参考着自己写了一个阿里巴巴一句话听写Nls的typescript模块。VUE3的组合式API形式 startClient:开始听写,注意下一步要尽快开启识别和传数据,否则6秒后会关闭 startRecognition…...
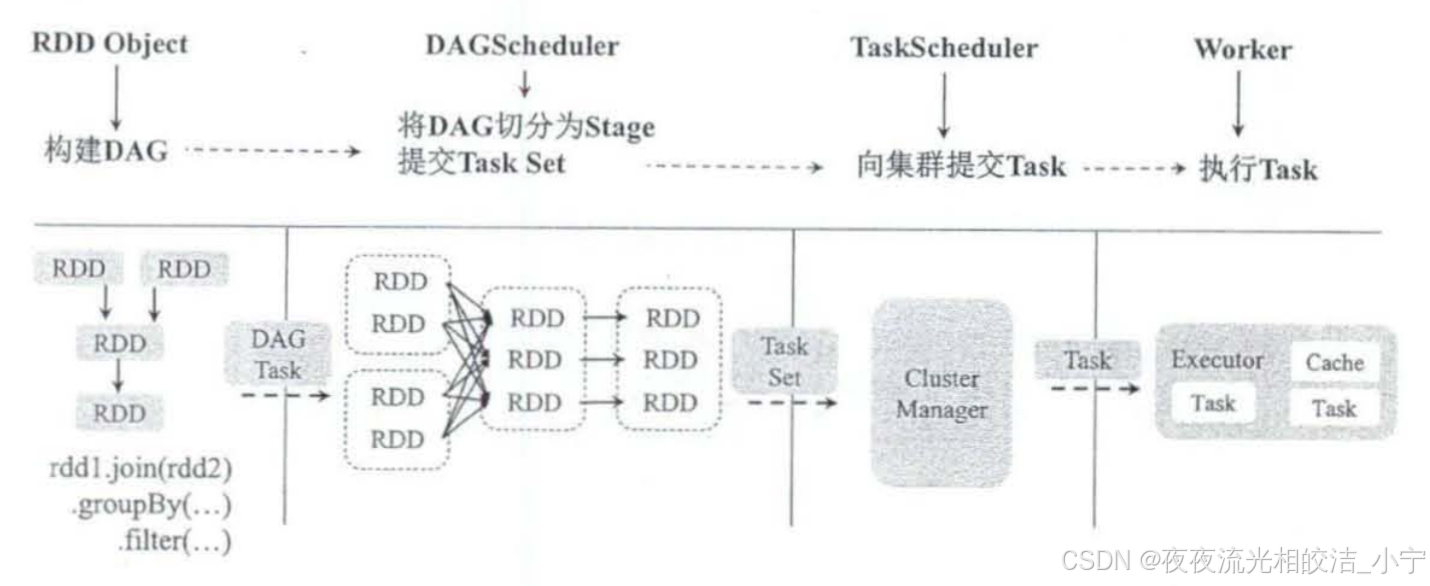
Apache Spark分布式计算框架架构介绍
目录 一、概述 二、Apache Spark架构组件栈 2.1 概述 2.2 架构图 2.3 架构分层组件说明 2.3.1 支持数据源 2.3.2 调度运行模式 2.3.3 Spark Core核心 2.3.3.1 基础设施 2.3.3.2 存储系统 2.3.3.3 调度系统 2.3.3.4 计算引擎 2.3.4 生态组件 2.3.4.1 Spark SQL 2.…...

Visual Studio 2019 (VS2019) 中使用 CMake 配置 OpenCV 库(快捷版)
2024.07.11 测试有效 最近需要用一下 opencv 处理图像,简单配置了一下Cmake下的 opencv 库。 没有编译 opencv ,也不知道他们为什么要自己编译 opencv 。 一、下载并安装 OpenCV 1.前往 OpenCV 官方网站 下载适用于您的系统的 OpenCV 安装包。 2.点击直接…...
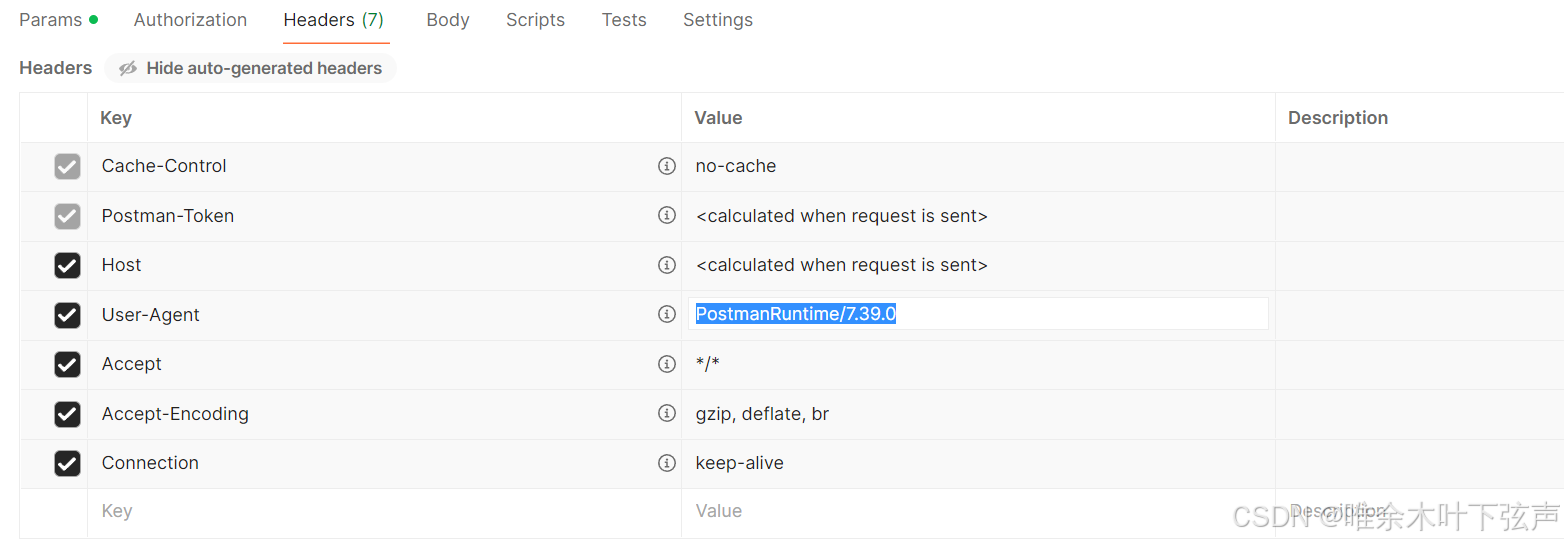
BUG解决:postman可以请求成功,但Python requests请求报403
目录 问题背景 问题定位 问题解决 问题背景 使用Python的requests库对接物联数据的接口之前一直正常运行,昨天突然请求不通了,通过进一步验证发现凡是使用代码调用接口就不通,而使用postman就能调通,请求参数啥的都没变。 接口…...

VScode常用快捷键
VScode介绍 VSCode(全称:Visual Studio Code)是一款由微软开发且跨平台的免费源代码编辑器。能够在windows、Linux、IOS等平台上运行,通过安装一些插件可以让这个编辑器变成一个编译器。与Visual Studio相比,它是免费…...
Day1每日编程题日记:数字统计、两个数组的交集、点击消除
前言:该篇用于记录自看。曾回看昨天的做题代码,竟然会觉得陌生,这竟然是我写的,细细读了一下,原来我当时是这么想的。因此我觉得记代码没有实际用处,重点是领悟了思想,这样子代码就在心中&#…...
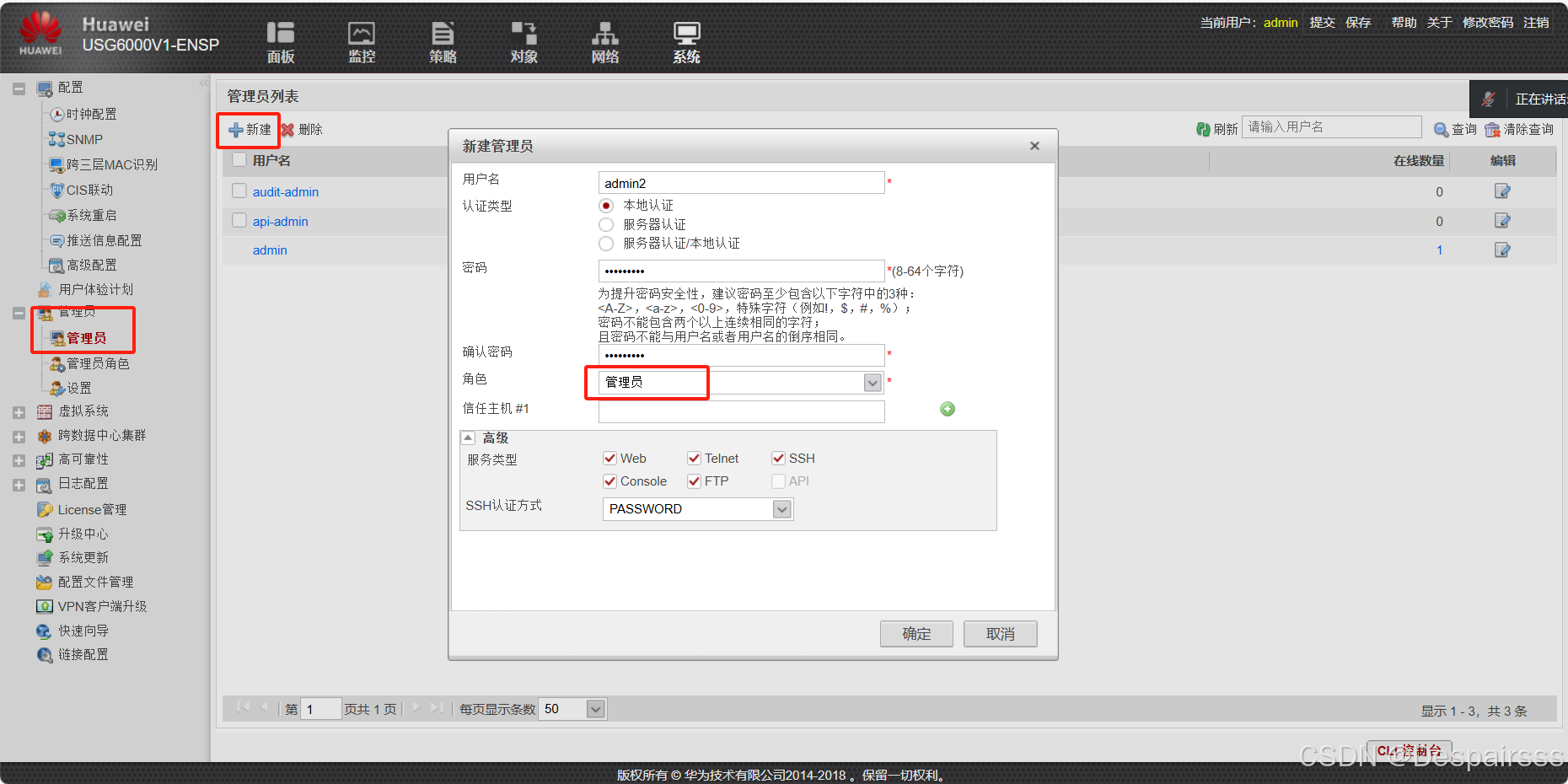
ENSP实现防火墙区域策略与用户管理
目录 实验拓扑与要求编辑 交换机与防火墙接口的配置 交换机: 创建vlan 接口配置 防火墙配置及接口配置 防火墙IP地址配置 云配置编辑编辑编辑 在浏览器上使用https协议登陆防火墙,并操作 访问网址:https://192.168.100.1:844…...

c#实现23种常见的设计模式--动态更新
c#实现23种常见的设计模式 设计模式通常分为三个主要类别: 创建型模式 结构型模式 行为型模式。 这些模式是用于解决常见的对象导向设计问题的最佳实践。 以下是23种常见的设计模式并且提供c#代码案例: 创建型模式: 1. 单例模式&#…...
昇思25天训练营Day11 - 基于 MindSpore 实现 BERT 对话情绪识别
模型简介 BERT全称是来自变换器的双向编码器表征量(Bidirectional Encoder Representations from Transformers),它是Google于2018年末开发并发布的一种新型语言模型。与BERT模型相似的预训练语言模型例如问答、命名实体识别、自然语言推理、…...

本地开发微信小程序,使用巴比达内网穿透
在微信小程序开发的热潮中,开发者常面临的一个挑战是如何在复杂的网络环境下测试和调试内网环境中的服务。巴比达正为这一难题提供了一条解决方案,极大简化了微信小程序与内网服务器之间通信的流程,加速了开发迭代周期。 以往,开…...

【LeetCode】快乐数
目录 一、题目二、解法完整代码 一、题目 编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变…...

大模型未来发展深度分析
大模型未来发展方向的深度探讨 近年来,人工智能技术的飞速发展,特别是大模型技术的崛起,为全球科技产业带来了前所未有的变革。大模型,以其强大的推理能力、创意生成能力和情绪智能,正在逐步成为推动社会经济发展的核…...
[线性RNN系列] Mamba: S4史诗级升级
前言 iclr24终于可以在openreview上看预印本了 这篇(可能是颠覆之作)文风一眼c re组出品;效果实在太惊艳了,实验相当完善,忍不住写一篇解读分享分享。 TL;DR (overview) Structured State-Sp…...

【鸿蒙学习笔记】元服务
官方文档:元服务规格 目录标题 什么是元服务特征第一个元服务-案例介绍创建项目源码启动模拟器启动entry创建卡片出发元服务 什么是元服务 特征 免安装分包预加载老化和更新机制 第一个元服务-案例介绍 创建项目 源码 Entry Component struct WidgetCard {buil…...

LIS+找规律,CF 582B - Once Again...
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 582B - Once Again... 二、解题报告 1、思路分析 考虑朴素做法对T *n的数组求LIS 但是T * n可达1e9 思考一下,最优解无非就是几个循环节拼接,我们最差情况下对sqrt(T)个a[]求LIS即…...
——开发:数据拆分——实施过程、应用特点)
数据赋能(145)——开发:数据拆分——实施过程、应用特点
实施过程 数据拆分的实施过程通常涉及以下几个关键步骤: 确定拆分目标和需求: 明确数据拆分的目的和需求,例如是为了减少数据处理的复杂性、提高查询效率还是为了满足特定的业务需求。根据需求确定拆分后的数据结构和拆分规则。选择拆分方法…...

【漏洞复现】Splunk Enterprise for Windows 任意文件读取漏洞 CVE-2024-36991
声明:本文档或演示材料仅用于教育和教学目的。如果任何个人或组织利用本文档中的信息进行非法活动,将与本文档的作者或发布者无关。 一、漏洞描述 Splunk Enterprise 是一款强大的机器数据管理和分析平台,广泛应用于企业中,用于实…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
