【期末考试复习】概率论与数理统计(知识点模式 - 复习题2)
题目:
设随机变量 X X X 的概率密度函数为 f ( x ) = a + b x f(x) = a + bx f(x)=a+bx,其中 0 < x ≤ 1 0 < x \leq 1 0<x≤1; f ( x ) = 0 f(x) = 0 f(x)=0,在其他情况下。已知 P ( X ≤ 1 / 2 ) = 3 / 8 P(X \leq 1/2) = 3/8 P(X≤1/2)=3/8,求 a a a 和 b b b。
涉及知识点:
- 概率密度函数(PDF):概率密度函数 f ( x ) f(x) f(x) 用于描述连续随机变量的概率分布,满足 ∫ − ∞ ∞ f ( x ) d x = 1 \int_{-\infty}^{\infty} f(x) \, dx = 1 ∫−∞∞f(x)dx=1。
- 累积分布函数(CDF):累积分布函数 F ( x ) F(x) F(x) 是 PDF 的积分,表示随机变量 X X X 小于或等于某个值 x x x 的概率,即 F ( x ) = ∫ − ∞ x f ( t ) d t F(x) = \int_{-\infty}^{x} f(t) \, dt F(x)=∫−∞xf(t)dt。
- 条件概率:利用已知条件计算随机变量的参数。
题目解答:
-
确定 a a a 和 b b b 的条件:
- 概率密度函数 f ( x ) f(x) f(x) 在 0 < x ≤ 1 0 < x \leq 1 0<x≤1 内有效,因此:
∫ 0 1 f ( x ) d x = 1 \int_0^1 f(x) \, dx = 1 ∫01f(x)dx=1
即:
∫ 0 1 ( a + b x ) d x = 1 \int_0^1 (a + bx) \, dx = 1 ∫01(a+bx)dx=1
- 概率密度函数 f ( x ) f(x) f(x) 在 0 < x ≤ 1 0 < x \leq 1 0<x≤1 内有效,因此:
-
计算累积分布函数 F ( x ) F(x) F(x):
- 对 f ( x ) = a + b x f(x) = a + bx f(x)=a+bx 进行积分得到 F ( x ) F(x) F(x),并利用已知条件 P ( X ≤ 1 / 2 ) = 3 / 8 P(X \leq 1/2) = 3/8 P(X≤1/2)=3/8:
F ( x ) = ∫ 0 x ( a + b x ) d x = a x + b x 2 2 F(x) = \int_0^x (a + bx) \, dx = ax + \frac{bx^2}{2} F(x)=∫0x(a+bx)dx=ax+2bx2
代入 x = 1 / 2 x = 1/2 x=1/2:
F ( 1 2 ) = a ⋅ 1 2 + b ( 1 2 ) 2 2 = a 2 + b 8 = 3 8 F\left(\frac{1}{2}\right) = a \cdot \frac{1}{2} + \frac{b \left(\frac{1}{2}\right)^2}{2} = \frac{a}{2} + \frac{b}{8} = \frac{3}{8} F(21)=a⋅21+2b(21)2=2a+8b=83
- 对 f ( x ) = a + b x f(x) = a + bx f(x)=a+bx 进行积分得到 F ( x ) F(x) F(x),并利用已知条件 P ( X ≤ 1 / 2 ) = 3 / 8 P(X \leq 1/2) = 3/8 P(X≤1/2)=3/8:
-
方程组求解 a a a 和 b b b:
-
利用归一化条件:
∫ 0 1 ( a + b x ) d x = [ a x + b x 2 2 ] 0 1 = a + b 2 = 1 \int_0^1 (a + bx) \, dx = \left[ ax + \frac{bx^2}{2} \right]_0^1 = a + \frac{b}{2} = 1 ∫01(a+bx)dx=[ax+2bx2]01=a+2b=1 -
利用 P ( X ≤ 1 / 2 ) = 3 / 8 P(X \leq 1/2) = 3/8 P(X≤1/2)=3/8:
a 2 + b 8 = 3 8 \frac{a}{2} + \frac{b}{8} = \frac{3}{8} 2a+8b=83
-
-
解方程组:
-
第一个方程:
a + b 2 = 1 a + \frac{b}{2} = 1 a+2b=1 -
第二个方程:
a 2 + b 8 = 3 8 \frac{a}{2} + \frac{b}{8} = \frac{3}{8} 2a+8b=83 -
消去 b b b 求解 a a a:
a 2 + b 8 = 3 8 ⇒ 4 a + b = 3 \frac{a}{2} + \frac{b}{8} = \frac{3}{8} \quad \Rightarrow \quad 4a + b = 3 2a+8b=83⇒4a+b=3
将 b = 2 − 2 a b = 2 - 2a b=2−2a 代入:
4 a + ( 2 − 2 a ) = 3 ⇒ 4 a + 2 − 2 a = 3 ⇒ 2 a = 1 ⇒ a = 1 2 4a + (2 - 2a) = 3 \quad \Rightarrow \quad 4a + 2 - 2a = 3 \quad \Rightarrow \quad 2a = 1 \quad \Rightarrow \quad a = \frac{1}{2} 4a+(2−2a)=3⇒4a+2−2a=3⇒2a=1⇒a=21 -
再求 b b b:
b = 2 − 2 a = 2 − 2 ⋅ 1 2 = 1 b = 2 - 2a = 2 - 2 \cdot \frac{1}{2} = 1 b=2−2a=2−2⋅21=1
-
结果:
a = 1 2 , b = 1 a = \frac{1}{2}, \quad b = 1 a=21,b=1
无偏估计量
定义:如果统计量 θ ^ \hat{\theta} θ^ 的期望值等于参数 θ \theta θ,即 E ( θ ^ ) = θ E(\hat{\theta}) = \theta E(θ^)=θ,则称 θ ^ \hat{\theta} θ^ 为参数 θ \theta θ 的无偏估计量。
意义:无偏估计量的期望值与真实参数值相等,这意味着在重复抽样的长期平均中,估计量不会系统性地偏离真实参数。
例子:对于正态分布 X ∼ N ( μ , σ 2 ) X \sim N(\mu, \sigma^2) X∼N(μ,σ2),样本均值 X ˉ = 1 n ∑ i = 1 n X i \bar{X} = \frac{1}{n} \sum_{i=1}^n X_i Xˉ=n1∑i=1nXi 是 μ \mu μ 的无偏估计量,因为 E ( X ˉ ) = μ E(\bar{X}) = \mu E(Xˉ)=μ。
最有效估计量
定义:在所有无偏估计量中,方差最小的估计量称为最有效估计量或最小方差无偏估计量(MVUE,Minimum Variance Unbiased Estimator)。
意义:最有效估计量在保证无偏的前提下,具有最小的估计误差(方差),因此在估计准确性方面是最优的。
例子:对于正态分布 X ∼ N ( μ , σ 2 ) X \sim N(\mu, \sigma^2) X∼N(μ,σ2),样本均值 X ˉ \bar{X} Xˉ 不仅是 μ \mu μ 的无偏估计量,而且由于它的方差最小(方差为 σ 2 n \frac{\sigma^2}{n} nσ2),所以 X ˉ \bar{X} Xˉ 是 μ \mu μ 的最有效估计量。
详细解释和联系
-
无偏性:一个估计量的无偏性保证了它的期望值等于被估计的参数值,从长期来看,这个估计量不会系统性地高估或低估参数。这是一个估计量的基本要求,但无偏性并不保证估计的效率。
-
方差:方差衡量了估计量的波动性。方差越小,估计量越集中在真实值附近,即估计越精确。
-
最小方差无偏估计量(MVUE):在所有无偏估计量中,最小方差无偏估计量是最优的,因为它在保证无偏性的前提下,具有最小的波动性。
实际应用中的步骤
- 验证无偏性:首先检查一个估计量是否是无偏的,即验证 E ( θ ^ ) = θ E(\hat{\theta}) = \theta E(θ^)=θ。
- 比较方差:在所有无偏估计量中,计算它们的方差,找出方差最小的那个。
- 确定最有效估计量:最小方差的无偏估计量即为最有效估计量。
题目:
若 X X X 服从自由度为 n n n 的 t t t 分布,则 X 2 X^2 X2 服从自由度为 什么的的 F F F 分布。
涉及知识点:
- t t t 分布:用于小样本量或总体方差未知情况下的均值比较。
- F F F 分布:用于比较两个样本方差是否显著不同,尤其在方差分析(ANOVA)中广泛应用。
题目解答:
t t t 分布与 F F F 分布的关系
如果随机变量 X ∼ t ( n ) X \sim t(n) X∼t(n),则 X 2 X^2 X2 服从自由度为 ( 1 , n ) (1, n) (1,n) 的 F F F 分布。详细推导如下:
-
t t t 分布定义:
如果 X ∼ t ( n ) X \sim t(n) X∼t(n),则 X X X 可表示为:
X = Z W n X = \frac{Z}{\sqrt{\frac{W}{n}}} X=nWZ其中:
- Z ∼ N ( 0 , 1 ) Z \sim N(0,1) Z∼N(0,1) 是标准正态分布。
- W ∼ χ 2 ( n ) W \sim \chi^2(n) W∼χ2(n) 是自由度为 n n n 的卡方分布。
-
平方 t t t 分布变量:
将 X X X 平方得到 X 2 X^2 X2:
X 2 = ( Z W n ) 2 = Z 2 W n = Z 2 W / n X^2 = \left( \frac{Z}{\sqrt{\frac{W}{n}}} \right)^2 = \frac{Z^2}{\frac{W}{n}} = \frac{Z^2}{W/n} X2= nWZ 2=nWZ2=W/nZ2 -
转化为 F F F 分布:
- Z 2 ∼ χ 2 ( 1 ) Z^2 \sim \chi^2(1) Z2∼χ2(1),因为 Z Z Z 是标准正态分布(一个标准正态分布)。
- W ∼ χ 2 ( n ) W \sim \chi^2(n) W∼χ2(n)。
- 因此, X 2 X^2 X2 服从自由度为 ( 1 , n ) (1, n) (1,n) 的 F F F 分布。
综上所述,如果 X ∼ t ( n ) X \sim t(n) X∼t(n),则 X 2 X^2 X2 服从自由度为 ( 1 , n ) (1, n) (1,n) 的 F F F 分布。
相关知识点补充
-
t t t 分布:适用于小样本量或总体方差未知情况下的均值比较,其概率密度函数为:
f ( t ) = Γ ( n + 1 2 ) n π Γ ( n 2 ) ( 1 + t 2 n ) − n + 1 2 f(t) = \frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n\pi} \, \Gamma\left(\frac{n}{2}\right)} \left(1 + \frac{t^2}{n}\right)^{-\frac{n+1}{2}} f(t)=nπΓ(2n)Γ(2n+1)(1+nt2)−2n+1
其中 Γ \Gamma Γ 是伽玛函数, n n n 是自由度。 -
F F F 分布:用于比较两个样本方差是否显著不同,其概率密度函数为:
f ( F ) = ( n 1 n 2 ) n 1 / 2 ( F n 1 n 2 ) n 1 2 − 1 B ( n 1 2 , n 2 2 ) ( 1 + n 1 n 2 F ) n 1 + n 2 2 f(F) = \frac{\left(\frac{n_1}{n_2}\right)^{n_1/2} \left(\frac{F}{\frac{n_1}{n_2}}\right)^{\frac{n_1}{2} - 1}}{B\left(\frac{n_1}{2}, \frac{n_2}{2}\right) \left(1 + \frac{n_1}{n_2} F\right)^{\frac{n_1+n_2}{2}}} f(F)=B(2n1,2n2)(1+n2n1F)2n1+n2(n2n1)n1/2(n2n1F)2n1−1
其中 B B B 是贝塔函数,自由度分别为 n 1 n_1 n1 和 n 2 n_2 n2。
END
相关文章:
)
【期末考试复习】概率论与数理统计(知识点模式 - 复习题2)
题目: 设随机变量 X X X 的概率密度函数为 f ( x ) a b x f(x) a bx f(x)abx,其中 0 < x ≤ 1 0 < x \leq 1 0<x≤1; f ( x ) 0 f(x) 0 f(x)0,在其他情况下。已知 P ( X ≤ 1 / 2 ) 3 / 8 P(X \leq 1/2) 3/…...

Jetpack Compose实现一个简单的微信UI
https://blog.csdn.net/News53231323/article/details/128509048 https://franzliszt1847.blog.csdn.net/article/details/129344822...

myeclipse开发ssm框架项目图书管理系统 mysql数据库web计算机毕业设计项目
摘 要 随着计算机的广泛应用,其逐步成为现代化的标志。图书馆的信息量也会越来越大,因此需要对图书信息、借书信息、还书信息等进行管理,及时了解各个环节中信息的变更,要对因此而产生的单据进行及时的处理,为了提高高…...

网络安全防御 -- 防火墙安全策略用户认证综合实验
实验拓扑: 实验目的: 1、DMZ区内的服务器,办公区仅能在办公时间内(9:00-18:00)可以访问,生产区的设备全天可以访问。 2、生产区不允许访问互联网,办公区和游客区允许访问互联网。 3、办公区设备10.0.2.10不允许访问DM…...

捷配笔记-PCB阻焊颜色对产品有什么影响?
阻焊层也称为阻焊层或阻焊剂。它是一种薄的聚合物层,应用于(PCB)。阻焊层的目的是保护PCB表面,并有助于防止焊桥。焊桥是两个导体之间的无意连接,通常是由于存在一小块焊料。需要注意的是,阻焊层被视为其单…...

网信大数据信用报告查询怎么查?网信大数据有什么作用?
随着互联网的快速发展,大数据技术已经广泛应用于各行各业。其中,网信大数据信用报告查询成为了许多人关注的焦点。那么,如何查询网信大数据信用报告呢?网信大数据又有哪些作用呢?本文将为您一一解答。 一、如何查询网信大数据信用报告? 要…...

【Vue】vue-element-admin组件化功能
1. 组件的封装 在vue-element-admin中,每个功能区域或UI元素都被封装成一个或多个Vue组件。这些组件可以是简单的按钮、输入框,也可以是复杂的表格、表单或页面布局。每个组件都包含了其模板(HTML结构)、逻辑(JavaScr…...

[论文笔记]涨点近5%! 以内容中心的检索增强生成可扩展的级联框架:Pistis-RAG
引言 今天带来一篇较新RAG的论文笔记:Pistis-RAG: A Scalable Cascading Framework Towards Content-Centric Retrieval-Augmented Generation。 在希腊神话中,Pistis象征着诚信、信任和可靠性。受到这些原则的启发,Pistis-RAG是一个可扩展…...
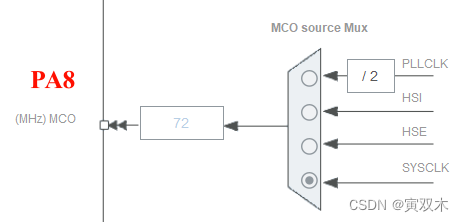
时钟系统框图(时钟树)解析
时钟系统框图(时钟树)解析 文章目录 时钟系统框图(时钟树)解析1、时钟树2、 4个时钟源:HSI、HSE、LSI、LSE3、PLL锁相环倍频输出4、系统时钟的来源5、Enable CSS(时钟监视系统)6、几个重要的时钟…...

DNS缓存详解
目录 一、缓存分类 1. 客户端缓存(以浏览器缓存为列) 2. 操作系统缓存 3.本地hosts文件静态映射 二、DNS查找优先顺序 1.浏览器查找顺序 2.cmd ping查找顺序(非浏览器) 一、缓存分类 在一台终端上,DNS缓存可以…...

一款好用的特殊字符处理工具
跟mybatis代码的时候,偶然发现的一款特殊字符处理工具java.lang.StringTokenizer。平常,我们看到的mybatis mapper.xml里面各种换行各种缩进,但日志文件里面的sql都是整整齐齐的。没有换行符,缩进等。就是利用该工具做的格式化处理…...

双重锁定:零信任沙箱 完美的安全保障
在当今数字化的世界中,企业的数据安全已成为至关重要的一环。随着云计算、移动互联和物联网等新技术的不断发展,传统的安全边界逐渐模糊,访问控制模式的局限性也日益凸显。为了应对这些挑战,零信任安全模型和苏州深信达的SDC沙盒技…...
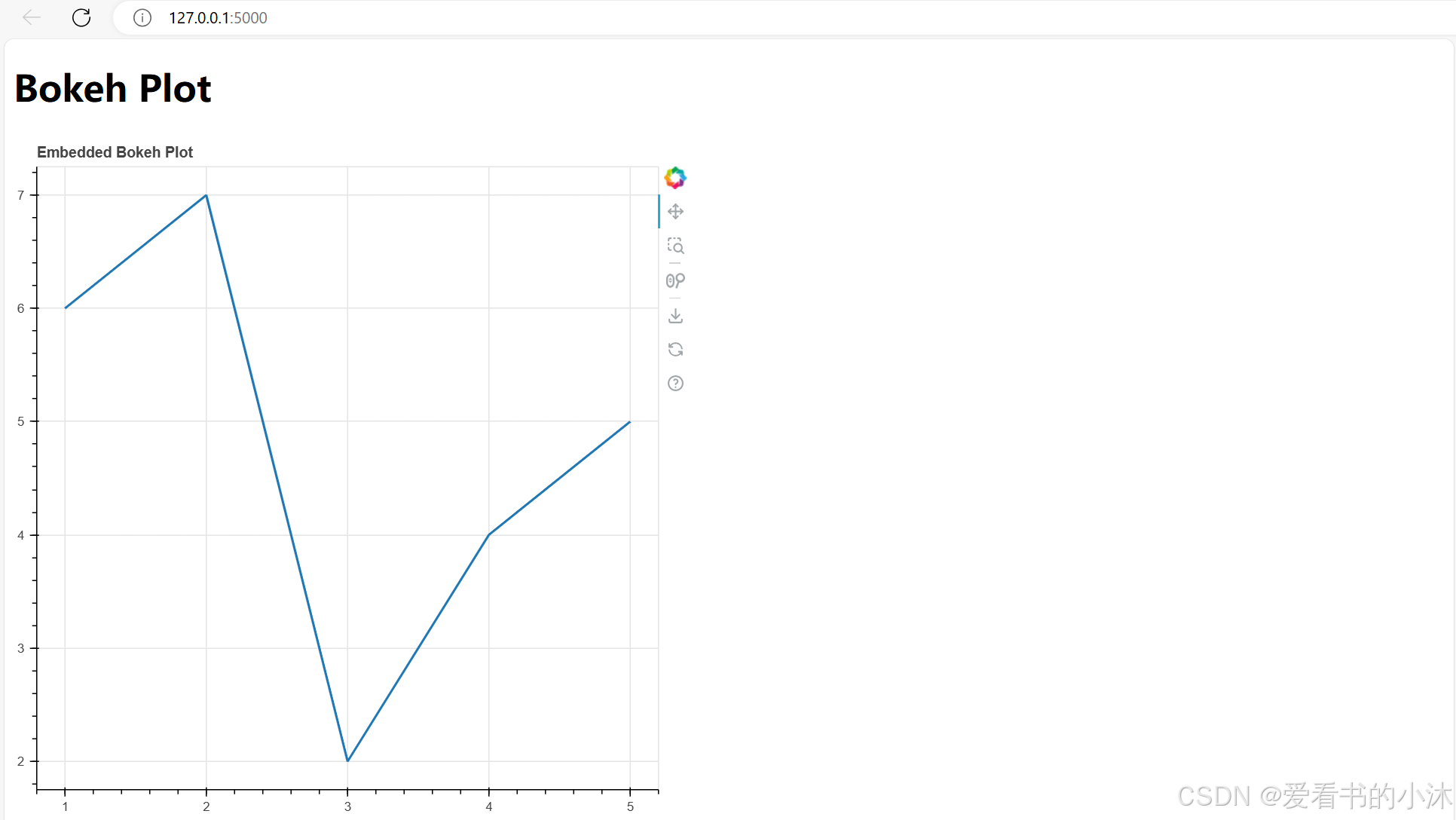
【小沐学Python】在线web数据可视化Python库:Bokeh
文章目录 1、简介2、安装3、测试3.1 创建折线图3.2 添加和自定义渲染器3.3 添加图例、文本和批注3.4 自定义您的绘图3.5 矢量化字形属性3.6 合并绘图3.7 显示和导出3.8 提供和筛选数据3.9 使用小部件3.10 嵌入Bokeh图表到Flask应用程序 结语 1、简介 https://bokeh.org/ https…...

GitHub 站点打不开
遇到的问题 您是否遇到过GitHub网站打不开的情况,正如下图所示: 解决方案 以下是一些常见的解决方案: 1. 检查网络连接 确保你的设备已连接到互联网。尝试访问其他网站,确保不是你的网络问题。 C:\Vinca>ping github.…...

前端开发工具
Lodash 有普通的 CommonJS 版本(通常称为 lodash)和 ES6 模块版本(称为 lodash-es)。它们的主要区别包括: 模块化:lodash 是传统的 CommonJS 模块,可使用 require 或 import 引入;lo…...

Everything搜索无法搜索到桌面的文件(无法检索C盘 或 特定路径的文件)
现象描述 在Everything搜索框中输入桌面已存在的文件或随便已知位置的文件,无法找到。 搜索时检索结果中明显缺少部分磁盘位置的,例如无法检索C盘,任意关键字搜索时结果中没有位于C盘的,无论怎样都搜不到C盘文件。 解决方法 在…...
Redux@4.x(1)- 核心概念)
React@16.x(52)Redux@4.x(1)- 核心概念
目录 1,MVC2,前端MVC的困难3,Flux4,Redux 1,MVC 是一个解决方案,用于降低 UI 和数据关联的复杂度。 在早期前后端未做分离时,服务端会响应一个完整的HTML,包含页面需要的所有数据。而…...

pytest系列——pytest_runtest_makereport钩子函数获取测试用例执行结果
前言 pytest测试框架提供的很多钩子函数方便我们对测试框架进行二次开发,可以根据自己的需求进行改造。 例如:钩子方法:pytest_runtest_makereport ,可以更清晰的了解测试用例的执行过程,并获取到每个测试用例的执行…...

Oracle数据库模式对象
文章目录 Oracle数据库模式对象 Oracle数据库模式对象 1、模式(schema)是一个数据库对象的集合。模式为一个数据库用户所有,与用户名字相同。通俗来说,模式对象就是一个用户。 2、 模式对象包括:聚簇、约束、数据库链接、触发器、维、外部过…...
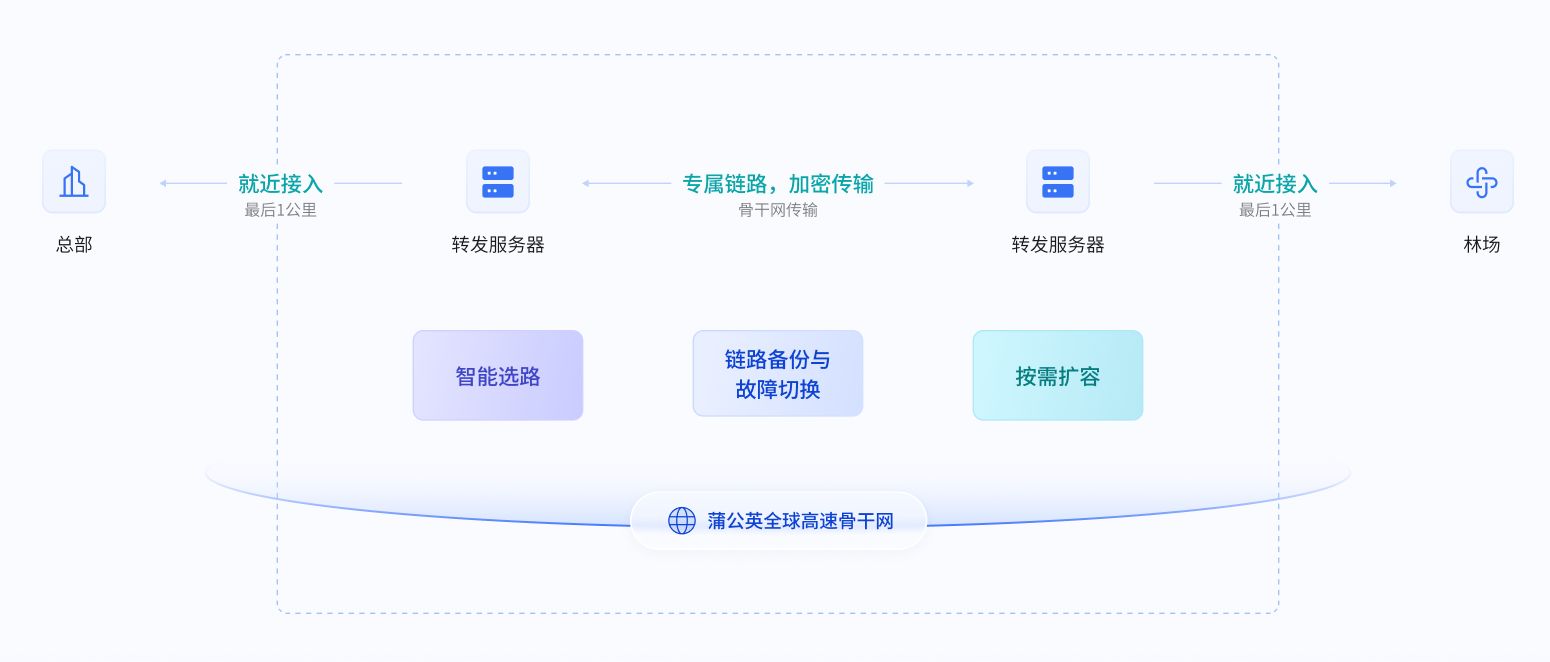
各地户外分散视频监控点位,如何实现远程集中实时监看?
公司业务涉及视频监控项目承包搭建,此前某个项目需求是为某林业公司提供视频监控解决方案,需要实现各地视频摄像头的集中实时监看,以防止国家储备林的盗砍、盗伐行为。 公司原计划采用运营商专线连接各个视频监控点位,实现远程视…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...

数据库优化实战指南:提升性能的黄金法则
在现代软件系统中,数据库性能直接影响应用的响应速度和用户体验。面对数据量激增、访问压力增大,数据库性能瓶颈经常成为项目痛点。如何科学有效地优化数据库,提升查询效率和系统稳定性,是每位开发与运维人员必备的技能。 本文结…...
