张量分解(4)——SVD奇异值分解
🍅 写在前面
👨🎓 博主介绍:大家好,这里是hyk写算法了吗,一枚致力于学习算法和人工智能领域的小菜鸟。
🔎个人主页:主页链接(欢迎各位大佬光临指导)
⭐️近期专栏:机器学习与深度学习
LeetCode算法实例
张量分解
张量分析系列知识,详见下方链接:
张量分解(1)——初探张量
张量分解(2)——张量运算
张量分解(3)——CP分解
张量分解(4)——SVD奇异值分解
张量分解(5)——Tucker分解
本系列文章主要参考论文:Tensor Decompositions and Applications∗
目录
- SVD原理
- SVD形式
- SVD计算
- SVD意义
- SVD分解示例
SVD原理
SVD奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,而可以使用这些小矩阵描述矩阵的重要的特性!和矩阵的特征值特征向量分解有所不同,SVD不需要矩阵为方阵,使用局限性更小。
SVD形式
SVD矩阵分解的形式为:
A = U Σ V T \mathrm{A}=\mathrm{U} \Sigma \mathrm{V}^{\mathrm{T}} A=UΣVT
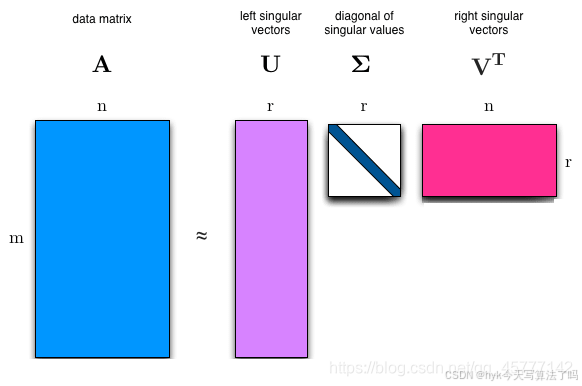
这里假设待分解的矩阵A为m×n维矩阵。U就是m×m维矩阵,名称为左奇异向量。Σ是m×n维矩阵,除了对角线元素,其他元素均是0,对角线元素就是奇异值。V的转置是n×n维的矩阵,名称为右奇异向量。
SVD计算
上面我们给除了SVD分解的形式,那么如何计算公式中的三个参数呢?
1、右奇异向量:
( A T A ) v i = λ i v i \left(A^T A\right) v_i=\lambda_i v_i (ATA)vi=λivi
我们对 ( A T A ) \left(A^T A\right) (ATA)矩阵求特征值特征向量后,这里的 v i vi vi就是右奇异向量,关于如何求矩阵特征值和特征向量,这里不再详细介绍。
2、奇异值
σ i = λ i \begin{aligned} & \sigma_{\mathrm{i}}=\sqrt{\lambda_{\mathrm{i}}} \\ \end{aligned} σi=λi
对上述特征值开方,即可求得奇异值。
3、左奇异向量
u i = 1 σ i A v i \begin{aligned} & & \mathrm{u}_{\mathrm{i}}=\frac{1}{\sigma_{\mathrm{i}}} A v_{\mathrm{i}} \end{aligned} ui=σi1Avi
求得奇异值与右奇异向量,二者按照上方公式计算即可得出左奇异向量。
最后将所求得的各个参数的分量合并在一起,按照形式排列,即可实现奇异值分解。
SVD意义
奇异值与矩阵特征值类似,在Σ矩阵中从大到小排列,但是奇异值减小的非常快,前10%的奇异值之和就占据奇异值总和的99%以上!我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。即: A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T \mathrm{A}_{\mathrm{m} \times \mathrm{n}}=\mathrm{U}_{\mathrm{m} \times \mathrm{m}} \Sigma_{\mathrm{m} \times \mathrm{n}} \mathrm{V}_{\mathrm{n} \times \mathrm{n}}^{\mathrm{T}} \approx \mathrm{U}_{\mathrm{m} \times \mathrm{k}} \Sigma_{\mathrm{k} \times \mathrm{k}} \mathrm{V}_{\mathrm{k} \times \mathrm{n}}^{\mathrm{T}} Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT
其中k比n要小很多。简而言之,SVD通过分解数据矩阵,帮助我们在降低数据维度的同时保留最重要的信息,这在数据压缩和去噪中非常有用。在推荐系统中,SVD通过揭示用户和物品的隐含特征,提升了推荐的准确性和个性化水平。
SVD分解示例
- 矩阵 A \boldsymbol{A} A 为: A = ( 0 1 1 1 1 0 ) \mathbf{A}=\left(\begin{array}{ll}0 & 1 \\ 1 & 1 \\ 1 & 0\end{array}\right) A= 011110
- 首先求出 A T A \boldsymbol{A}^T \boldsymbol{A} ATA 和 A A T \boldsymbol{A} \boldsymbol{A}^T AAT
A T A = ( 0 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 2 1 1 2 ) A A T = ( 0 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 1 1 0 1 2 1 0 1 1 ) \begin{aligned} & \mathbf{A}^{\mathrm{T}} \mathbf{A}=\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)=\left(\begin{array}{ll} 2 & 1 \\ 1 & 2 \end{array}\right) \\ & \mathbf{A A}^{\mathrm{T}}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)=\left(\begin{array}{lll} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 1 \end{array}\right) \\ & \end{aligned} ATA=(011110) 011110 =(2112)AAT= 011110 (011110)= 110121011 - 进而分别求出 A T A \boldsymbol{A}^T \boldsymbol{A} ATA 和 A A T \boldsymbol{A} \boldsymbol{A}^T AAT 的特征值和特征向量:
A T A : λ 1 = 3 ; v 1 = ( 1 / 2 1 / 2 ) ; λ 2 = 1 ; v 2 = ( − 1 / 2 1 / 2 ) A A T : λ 1 = 3 ; u 1 = ( 1 / 6 2 / 6 1 / 6 ) ; λ 2 = 1 ; u 2 = ( 1 / 2 0 − 1 / 2 ) ; λ 3 = 0 ; u 3 = ( 1 / 3 − 1 / 3 1 / 3 ) \begin{aligned} & \boldsymbol{A}^{\boldsymbol{T}} \boldsymbol{A}: \lambda_1=3 ; \mathrm{v}_1=\binom{1 / \sqrt{2}}{1 / \sqrt{2}} ; \lambda_2=1 ; \mathrm{v}_2=\binom{-1 / \sqrt{2}}{1 / \sqrt{2}} \\ & \boldsymbol{A} \boldsymbol{A}^T: \lambda_1=3 ; \mathrm{u}_1=\left(\begin{array}{c} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) ; \lambda_2=1 ; \mathrm{u}_2=\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) ; \lambda_3=0 ; \mathrm{u}_3= \\ & \left(\begin{array}{c} 1 / \sqrt{3} \\ -1 / \sqrt{3} \\ 1 / \sqrt{3} \end{array}\right) \end{aligned} ATA:λ1=3;v1=(1/21/2);λ2=1;v2=(1/2−1/2)AAT:λ1=3;u1= 1/62/61/6 ;λ2=1;u2= 1/20−1/2 ;λ3=0;u3= 1/3−1/31/3
利用 A v i = σ i u i , i = 1 , 2 A v_i=\sigma_i u_i, i=1,2 Avi=σiui,i=1,2 求奇异值:
( 0 1 1 1 1 0 ) ( 1 / 2 1 / 2 ) = σ 1 ( 1 / 6 2 / 6 1 / 6 ) ⇒ σ 1 = 3 ( 0 1 1 1 1 0 ) ( − 1 / 2 1 / 2 ) = σ 2 ( 1 / 2 0 − 1 / 2 ) ⇒ σ 2 = 1 \begin{aligned} & \left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\binom{1 / \sqrt{2}}{1 / \sqrt{2}}=\sigma_1\left(\begin{array}{l} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) \Rightarrow \sigma_1=\sqrt{3} \\ & \left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\binom{-1 / \sqrt{2}}{1 / \sqrt{2}}=\sigma_2\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) \Rightarrow \sigma_2=1 \end{aligned} 011110 (1/21/2)=σ1 1/62/61/6 ⇒σ1=3 011110 (1/2−1/2)=σ2 1/20−1/2 ⇒σ2=1
也可以用 σ i = λ i \sigma_i=\sqrt{\lambda_i} σi=λi 直接求!
再利用左奇异值求解公式,可得左奇异值。
最终得到A的奇异值分解为:
A = U Σ V T = ( 1 / 6 1 / 2 1 / 3 2 / 6 0 − 1 / 3 1 / 6 − 1 / 2 1 / 3 ) ( 3 0 0 1 0 0 ) ( 1 / 2 1 / 2 − 1 / 2 1 / 2 ) \mathrm{A}=\mathrm{U} \Sigma \mathrm{V}^{\mathrm{T}}=\left(\begin{array}{ccc} 1 / \sqrt{6} & 1 / \sqrt{2} & 1 / \sqrt{3} \\ 2 / \sqrt{6} & 0 & -1 / \sqrt{3} \\ 1 / \sqrt{6} & -1 / \sqrt{2} & 1 / \sqrt{3} \end{array}\right)\left(\begin{array}{cc} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right)\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ -1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right) A=UΣVT= 1/62/61/61/20−1/21/3−1/31/3 300010 (1/2−1/21/21/2)
相关文章:

张量分解(4)——SVD奇异值分解
🍅 写在前面 👨🎓 博主介绍:大家好,这里是hyk写算法了吗,一枚致力于学习算法和人工智能领域的小菜鸟。 🔎个人主页:主页链接(欢迎各位大佬光临指导) ⭐️近…...

第三方配件也能适配苹果了,iOS 18与iPadOS 18将支持快速配对
苹果公司以其对用户体验的不懈追求和对创新技术的不断探索而闻名。随着iOS 18和iPadOS 18的发布,苹果再次证明了其在移动操作系统领域的领先地位。 最新系统版本中的一项引人注目的功能,便是对蓝牙和Wi-Fi配件的配对方式进行了重大改进,不仅…...

Docker 部署 Nginx 并在容器内配置申请免费 SSL 证书
文章目录 dockerdocker-compose.yml申请免费 SSL 证书请求头参数带下划线 docker https://hub.docker.com/_/nginx docker pull nginx:1.27注: 国内网络原因无法下载镜像,nginx 镜像文件下载链接 https://pan.baidu.com/s/1O35cPbx6AHWUJL1v5-REzA?pw…...
模型评估与选择
2.1 经验误差与过拟合 错误率(error rate): 分类错误的样本数占样本总数的比例 精度(accuracy):1- 错误率 训练误差 / 经验误差:在训练集上的误差 泛化误差:在新样本上的误差 过…...

有必要把共享服务器升级到VPS吗?
根据自己的需求来选择是否升级,虚拟专用服务器 (VPS) 是一种托管解决方案,它以低得多的成本提供专用服务器的大部分功能。使用 VPS,您的虚拟服务器将与在其上运行的其他虚拟服务器共享硬件服务器的资源。但是,与传统的共享托管&am…...
LLM代理应用实战:构建Plotly数据可视化代理
如果你尝试过像ChatGPT这样的LLM,就会知道它们几乎可以为任何语言或包生成代码。但是仅仅依靠LLM是有局限的。对于数据可视化的问题我们需要提供一下的内容 描述数据:模型本身并不知道数据集的细节,比如列名和行细节。手动提供这些信息可能很麻烦&#…...

大模型系列3--pytorch dataloader的原理
pytorch dataloader运行原理 1. 背景2. 环境搭建2.1. 安装WSL & vscode2.2. 安装conda & pytorch_gpu环境 & pytorch 2.112.3 命令行验证python环境2.4. vscode启用pytorch_cpu虚拟环境 3. 调试工具3.1. vscode 断点调试3.2. py-spy代码栈探测3.3. gdb attach3.4. …...

SQLServer 如何设置端口
在SQL Server中,可以通过以下步骤设置端口: 打开SQL Server配置管理器。可以在开始菜单中搜索“SQL Server配置管理器”来找到它。 在左侧导航窗格中,展开“SQL Server网络配置”节点。 选择你要配置的实例,如“SQL Server Netw…...

调整网络安全策略以适应不断升级的威胁形势
关键网络安全统计数据和趋势 当今数字时代网络安全的重要性...
9. 回文数)
(leetcode学习)9. 回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数 是指正序(从左向右)和倒序(从右向左)读都是一样的整数。 例如,121 是回文,而…...
QT VTK 简单测试工程
目录 1 目录结构 2 文件源码 3 运行结果 4 报错及处理 使用编译好的VTK库进行测试 1 目录结构 2 文件源码 Pro文件 QT core guigreaterThan(QT_MAJOR_VERSION, 4): QT widgetsCONFIG c17# You can make your code fail to compile if it uses deprecated APIs. #…...
)
ES6 Generator函数的异步应用 (八)
ES6 Generator 函数的异步应用主要通过与 Promise 配合使用来实现。这种模式被称为 “thunk” 模式,它允许你编写看起来是同步的异步代码。 特性: 暂停执行:当 Generator 函数遇到 yield 表达式时,它会暂停执行,等待 …...
Navicat:打造高效数据库管理之道
1. 导言 1.1 介绍Navicat Navicat是一款功能强大的数据库管理工具,旨在帮助用户高效地管理多种类型的数据库,包括MySQL、PostgreSQL、Oracle、SQL Server等。通过Navicat,用户可以轻松地进行数据库的创建、编辑、备份、同步和调试等操作,极大地简化了数据库管理的复杂性。…...
Python和C++全球导航卫星系统和机器人姿态触觉感知二分图算法
🎯要点 🎯马尔可夫随机场网格推理学习 | 🎯二维伊辛模型四连网格模型推理 | 🎯统计物理学模型扰动与最大乘积二值反卷积 | 🎯受限玻尔兹曼机扰动和最大乘积采样 | 🎯视觉概率生成模型测试图像 dz…...
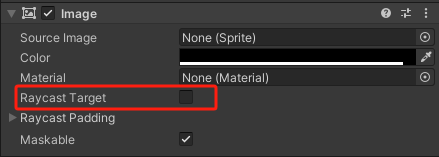
Unity 优化合集
1️⃣ 贴图优化 1. Read/Write Enable 这个属性勾选后允许你在运行时读取和写入纹理数据,这对于需要实时生成内容或者需要动态修改纹理的场合非常有用但在大部分情况下这是不必要的。如果打开这个属性,会使运行时贴图大小翻倍,内存中会额外…...

第九届MathorCup高校数学建模挑战赛-A题:基于数据驱动的城市轨道交通网络优化研究
目录 摘 要 一、 问题的提出 二、 基本假设 三、 符号说明 四、 问题分析 4.1 问题 1 的分析 4.2 问题 2 的分析 4.3 问题 3 的分析 4.4 问题 4 的分析 五、 问题 1 的模型建立与求解 5.1 问题分析 5.2 数据处理 5.2.1 数据统计 5.2.2 异常数据处理方法 5.2.3 剔除异常数据值 5…...
Spring webflux基础核心技术
一、 用操作符转换响应式流 1 、 映射响应式流元素 转换序列的最自然方式是将每个元素映射到一个新值。 Flux 和 Mono 给出了 map 操作符,具有 map(Function<T,R>) 签名的方法可用于逐个处理元素。 当操作符将元素的类型从 T 转变为 R 时…...
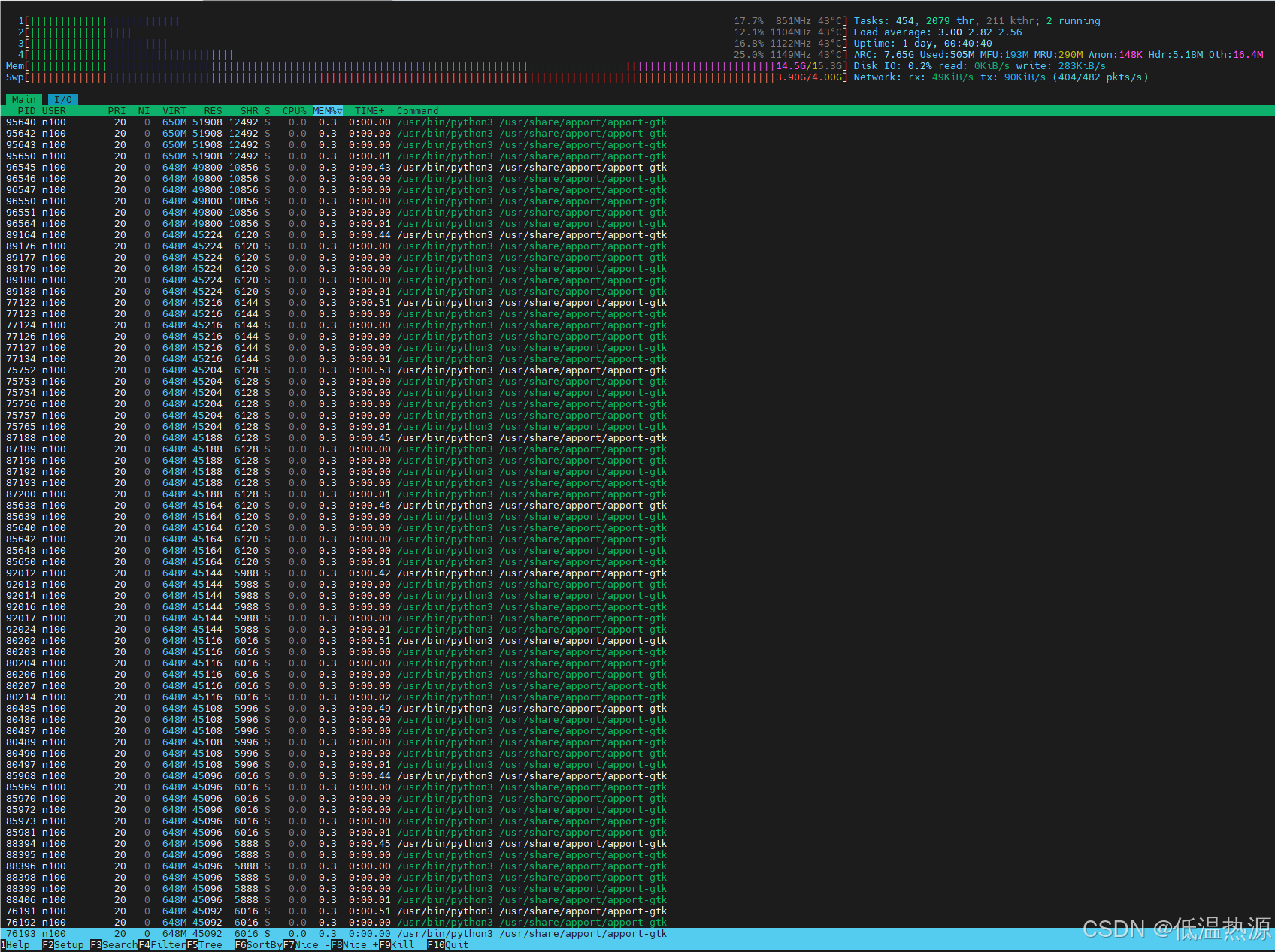
关闭Ubuntu烦人的apport
先来看让人绷不住的(恼) 我查半天apport是啥玩意发现就一错误报告弹窗,十秒钟给我弹一次一天给我内存弹爆了 就算我程序就算真的不停崩溃,也没你这傻比apport杀伤性强啊??? 原则上是不建议关闭…...

海事无人机解决方案
海事巡察 海事巡察现状 巡查效率低下,存在视野盲区,耗时长,人力成本高。 海事的职能 统一管理水上交通安全和防治船舶污染。 管理通航秩序、通航环境。负责水域的划定和监督管理,维护水 上交通秩序;核定船舶靠泊安…...

Docker--在linux安装软件
Docker 引用Docker原因是在linux中安装软件 以前在linux中安装软件,是直接安装在linux操作系统上,软件和操作系统耦合度很高,不方便管理,因为linux版本不同,环境也就改变了 docker是一种容器技术,提供标…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
