数学基础 -- 三角学
三角学
三角学(Trigonometry)是数学的一个分支,主要研究三角形的边长与角度之间的关系。三角学在几何学、物理学、工程学等多个领域中有广泛的应用。以下是三角学的一些基本概念和公式:
基本概念
- 直角三角形:一个角为90度的三角形。
- 斜边:直角三角形中最长的边,对应于直角的对边。
- 对边:某个角的对边。
- 邻边:某个角的邻边。
三角函数
- 正弦函数 (sin): sin ( θ ) = 对边 斜边 \sin(θ) = \frac{对边}{斜边} sin(θ)=斜边对边
- 余弦函数 (cos): cos ( θ ) = 邻边 斜边 \cos(θ) = \frac{邻边}{斜边} cos(θ)=斜边邻边
- 正切函数 (tan): tan ( θ ) = 对边 邻边 \tan(θ) = \frac{对边}{邻边} tan(θ)=邻边对边
倒数三角函数
- 余割函数 (csc): csc ( θ ) = 1 sin ( θ ) \csc(θ) = \frac{1}{\sin(θ)} csc(θ)=sin(θ)1
- 正割函数 (sec): sec ( θ ) = 1 cos ( θ ) \sec(θ) = \frac{1}{\cos(θ)} sec(θ)=cos(θ)1
- 余切函数 (cot): cot ( θ ) = 1 tan ( θ ) \cot(θ) = \frac{1}{\tan(θ)} cot(θ)=tan(θ)1
常用三角公式
- sin 2 ( θ ) + cos 2 ( θ ) = 1 \sin^2(θ) + \cos^2(θ) = 1 sin2(θ)+cos2(θ)=1
- 1 + tan 2 ( θ ) = sec 2 ( θ ) 1 + \tan^2(θ) = \sec^2(θ) 1+tan2(θ)=sec2(θ)
- 1 + cot 2 ( θ ) = csc 2 ( θ ) 1 + \cot^2(θ) = \csc^2(θ) 1+cot2(θ)=csc2(θ)
常用角度的三角函数值
| 角度(θ) | sin ( θ ) \sin(\theta) sin(θ) | cos ( θ ) \cos(θ) cos(θ) | tan ( θ ) \tan(θ) tan(θ) |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1 2 \frac{1}{2} 21 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 3 \frac{1}{\sqrt{3}} 31 |
| 45° | 2 2 \frac{\sqrt{2}}{2} 22 | 2 2 \frac{\sqrt{2}}{2} 22 | 1 |
| 60° | 3 2 \frac{\sqrt{3}}{2} 23 | 1 2 \frac{1}{2} 21 | 3 \sqrt{3} 3 |
| 90° | 1 1 1 | 0 0 0 | ∞ ∞ ∞ |
应用
- 解三角形:利用已知的角度和边长求解未知的角度和边长。
- 波动和振动:正弦和余弦函数在描述波动和振动现象中具有重要作用。
- 导航与定位:在GPS定位和航海中,三角函数用于计算位置和方向。
扩展三角函数定义域
扩展三角函数定义域是指将三角函数(如正弦函数、余弦函数、正切函数等)从它们在基本定义中的常见定义域(通常是角度或弧度的有限范围)扩展到更广泛的范围,通常是整个实数集。下面是一些方法和概念,帮助你理解和扩展三角函数的定义域:
-
周期性:
- 三角函数的一个基本特性是周期性。例如,正弦函数和余弦函数的周期为 2 π 2\pi 2π,即对于任意实数 x x x,都有 sin ( x + 2 π ) = sin ( x ) \sin(x + 2\pi) = \sin(x) sin(x+2π)=sin(x) 和 cos ( x + 2 π ) = cos ( x ) \cos(x + 2\pi) = \cos(x) cos(x+2π)=cos(x)。
- 正切函数的周期为 π \pi π,即 tan ( x + π ) = tan ( x ) \tan(x + \pi) = \tan(x) tan(x+π)=tan(x)。
-
无限扩展:
- 利用周期性,可以将三角函数的定义从一个有限区间扩展到整个实数集。例如,考虑正弦函数的基本定义域是 [ − π , π ] [- \pi, \pi] [−π,π],通过利用其周期性,可以定义 sin ( x ) \sin(x) sin(x) 在整个实数范围上。
-
复数扩展:
- 三角函数还可以扩展到复数域。通过欧拉公式 e i x = cos ( x ) + i sin ( x ) e^{ix} = \cos(x) + i\sin(x) eix=cos(x)+isin(x),可以将三角函数扩展为复变量的函数。
- 例如,定义复数 z = x + i y z = x + iy z=x+iy,那么正弦函数的扩展为 sin ( z ) = sin ( x + i y ) = sin ( x ) cosh ( y ) + i cos ( x ) sinh ( y ) \sin(z) = \sin(x + iy) = \sin(x)\cosh(y) + i\cos(x)\sinh(y) sin(z)=sin(x+iy)=sin(x)cosh(y)+icos(x)sinh(y),这里 cosh \cosh cosh 和 sinh \sinh sinh 分别是双曲余弦和双曲正弦函数。
-
反函数的扩展:
- 三角函数的反函数(如反正弦、反余弦、反正切)通常有有限的定义域。例如,反正弦函数 sin − 1 ( x ) \sin^{-1}(x) sin−1(x) 的定义域为 [ − 1 , 1 ] [-1, 1] [−1,1],值域为 [ − π / 2 , π / 2 ] [- \pi/2, \pi/2] [−π/2,π/2]。
- 通过考虑这些函数的周期性,可以将其值域扩展到更广范围。
-
特定应用场景:
- 在一些应用中,特别是信号处理和傅里叶分析中,三角函数的定义域需要扩展到整个实数集,以处理无限时间范围内的信号。
举个具体例子,如果你想将正弦函数从基本定义域 [ 0 , 2 π ] [0, 2\pi] [0,2π] 扩展到整个实数集,可以利用它的周期性:
sin ( x ) = sin ( x + 2 k π ) \sin(x) = \sin(x + 2k\pi) sin(x)=sin(x+2kπ)
其中 k k k 是任何整数。因此,对于任意实数 x x x,总可以找到一个整数 k k k,使得 x + 2 k π x + 2k\pi x+2kπ 落在 [ 0 , 2 π ] [0, 2\pi] [0,2π] 这个区间内,从而定义 sin ( x ) \sin(x) sin(x) 的值。
通过这些方法,可以有效地将三角函数的定义域扩展到更广的范围,使其适用于更多的数学和工程问题。
相关文章:

数学基础 -- 三角学
三角学 三角学(Trigonometry)是数学的一个分支,主要研究三角形的边长与角度之间的关系。三角学在几何学、物理学、工程学等多个领域中有广泛的应用。以下是三角学的一些基本概念和公式: 基本概念 直角三角形:一个角…...

基于BitMap的工作日间隔计算
背景问题 在我们实际开发过程中,时常会遇到日期的间隔计算,即计算多少工作日之后的日期,在不考虑法定节假日的情况下也不是那么复杂,毕竟周六、周日是相对固定的,Java语言也提供了丰富的类来处理此问题。 然而&#x…...

sqlite3 — DB-API 2.0 interface for SQLite databases
sqlite3 — DB-API 2.0 interface for SQLite databases — Python 3.12.4 documentation sqlite3 — DB-API 2.0 interface for SQLite databasessqlite3 — SQLite数据库的DB-API 2.0接口 Source code: Lib/sqlite3/ 源代码位置:Lib/sqlite3/ SQLite is a C…...

Spring Boot中的安全配置与实现
Spring Boot中的安全配置与实现 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨Spring Boot中的安全配置与实现,看看如何保护你的…...

DepthAnything(2): 基于ONNXRuntime在ARM(aarch64)平台部署DepthAnything
DepthAnything(1): 先跑一跑Depth Anything_depth anything离线怎么跑-CSDN博客 目录 1. 写在前面 2. 安装推理组件 3. 生成ONNX 4. 准备ONNXRuntime库 5. API介绍 6. 例程 1. 写在前面 DepthAnything是一种能在任何情况下处理任何图像的简单却又强大的深度估计模型。 …...

JAVA简单封装UserUtil
目录 思路 一、TokenFilterConfiguration 二、FilterConfig 三、TokenContextHolder 四、TokenUtil 五、UserUtil 思路 配置Token过滤器(TokenFilterConfiguration):实现一个Token过滤器配置,用于拦截HTTP请求,从请求头中提取Token&…...

【TOOLS】Chrome扩展开发
Chrome Extension Development 1. 入门教程 入门案例,可以访问【 谷歌插件官网官方文档 】查看官方入门教程,这里主要讲解大概步骤 Chrome Extenson 没有固定的脚手架,所以项目的搭建需要根据开发者自己根据需求搭建项目(例如通过…...

分享WPF的UI开源库
文章目录 前言一、HandyControl二、AduSkin三、Adonis UI四、Panuon.WPF.UI五、LayUI-WPF六、MahApps.Metro七、MaterialDesignInXamlToolkit八、FluentWPF九、DMSkin总结 前言 分享WPF的UI开源库。 一、HandyControl HandyControl是一套WPF控件库,它几乎重写了所…...
[ACM独立出版]2024年虚拟现实、图像和信号处理国际学术会议(ICVISP 2024)
最新消息ICVISP 2024-已通过ACM出版申请投稿免费参会,口头汇报或海报展示(可获得相应证明证书) ————————————————————————————————————————— [ACM独立出版]2024年虚拟现实、图像和信号处理国际学术会议(ICVI…...

JVM:类加载器
文章目录 一、什么是类加载器二、类加载器的应用场景三、类加载器的分类1、分类2、启动类加载器3、Java中的默认类加载器(1)扩展类加载器(2)应用程序类加载器(3)arthas中类加载器相关的功能 四、双亲委派机…...

支持向量机 (support vector machine,SVM)
支持向量机 (support vector machine,SVM) flyfish 支持向量机是一种用于分类和回归的机器学习模型。在分类任务中,SVM试图找到一个最佳的分隔超平面,使得不同类别的数据点在空间中被尽可能宽的间隔分开。 超平面方…...

宝塔面板以www用户运行composer
方式一 执行命令时指定www用户 sudo -u www composer update方式二 在网站配置中的composer选项卡中选择配置运行...

昇思25天打卡营-mindspore-ML- Day24-基于 MindSpore 实现 BERT 对话情绪识别
学习笔记:基于MindSpore实现BERT对话情绪识别 算法原理 BERT(Bidirectional Encoder Representations from Transformers)是由Google于2018年开发的一种预训练语言表示模型。BERT的核心原理是通过在大量文本上预训练深度双向表示࿰…...

【精品资料】模块化数据中心解决方案(33页PPT)
引言:模块化数据中心解决方案是一种创新的数据中心设计和部署策略,旨在提高数据中心的灵活性、可扩展性和效率。这种方案通过将数据中心的基础设施、计算、存储和网络资源封装到标准化的模块中,实现了快速部署、易于管理和高效运维的目标 方案…...

N6 word2vec文本分类
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊# 前言 前言 上周学习了训练word2vec模型,这周进行相关实战 1. 导入所需库和设备配置 import torch import torch.nn as nn import torchvision …...
excel、word、ppt 下载安装步骤整理
请按照我的步骤开始操作,注意以下截图红框标记处(往往都是需要点击的地方) 第一步:下载 首先进入office下载网址: otp.landian.vip 然后点击下载 拉到下方 下载站点(这里根据自己的需要选择下载&#x…...

【python学习】标准库之日期和时间库定义、功能、使用场景和示例
引言 datetime模块最初是由 Alex Martelli 在 Python 2.3 版本引入的,目的是为了解决之前版本中处理日期和时间时存在的限制和不便 在datetime模块出现之前,Python 主要使用time模块来处理时间相关的功能,但 time模块主要基于 Unix 纪元时间&…...

Android --- Kotlin学习之路:基础语法学习笔记
------>可读可写变量 var name: String "Hello World";------>只读变量 val name: String "Hello World"------>类型推断 val name: String "Hello World" 可以写成 val name "Hello World"------>基本数据类型 1…...
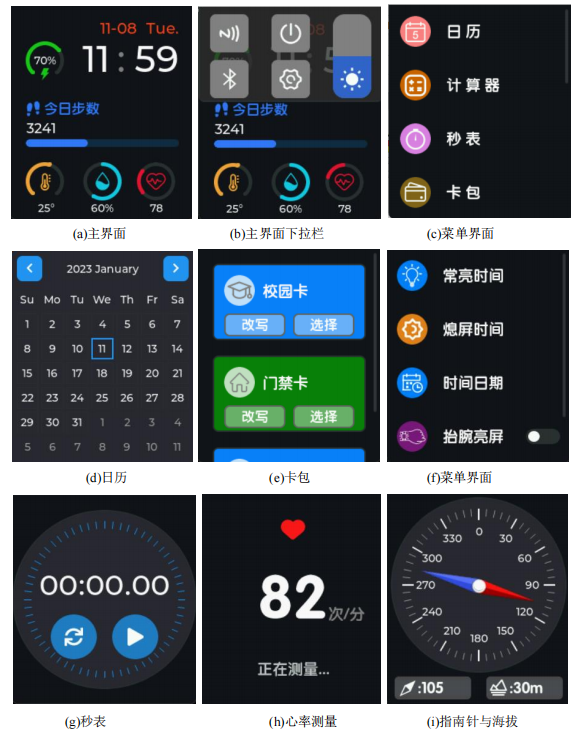
嵌入式智能手表项目实现分享
简介 这是一个基于STM32F411CUE6和FreeRTOS和LVGL的低成本的超多功能的STM32智能手表~ 推荐 如果觉得这个手表的硬件难做,又想学习相关的东西,可以试下这个新出的开发板,功能和例程demo更多!FriPi炸鸡派STM32F411开发板: 【STM32开发板】 FryPi炸鸡派 - 嘉立创EDA开源硬件平…...

`nmap`模块是一个用于与Nmap安全扫描器交互的库
在Python中,nmap模块是一个用于与Nmap安全扫描器交互的库。Nmap(Network Mapper)是一个开源工具,用于发现网络上的设备和服务。虽然Python的nmap模块可能不是官方的Nmap库(因为Nmap本身是用C/C编写的)&…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
