电机泵盖机器人打磨去毛刺,选德国进口高精度主轴
机器人打磨去毛刺该如何选择主轴呢?首先我们需要考虑的是工件的材质,电机泵盖通常使用铸铁、不锈钢、合金钢等金属材质,因此这类保持的硬度较高,一般会选择功率、扭矩较大的德国进口高精度主轴Kasite 4060 ER-S。

Kasite 4060 ER-S,最高转速50,000rpm,功率2,000W,扭矩215Ncm,保证了在高速旋转的同时能够输出足够的力度,对工件进行有效的打磨和去毛刺。

此外,Kasite 4060 ER-S主轴还具备高精度和稳定性,锥面跳动通常≤1μm,并且先进的制造工艺和精密的控制系统,在电机泵盖打磨去毛刺工艺中能够在长时间连续工作的情况下保持恒定转速和输出力度,提高了去毛刺加工质量。
Kasite 4060 ER-S作为德国进口的高精度主轴,在电机泵盖打磨去毛刺工艺中具有明显的优势,其强大的性能、高精度和稳定性以及广泛的应用范围和成功案例支持,成为金属非金属切割、铣削、钻孔、打磨去毛刺等加工的良好选择。
如想获取更多去毛刺方案请咨询速科德电机科技Kasite丨德国SycoTec亚太服务中心。
相关文章:

电机泵盖机器人打磨去毛刺,选德国进口高精度主轴
机器人打磨去毛刺该如何选择主轴呢?首先我们需要考虑的是工件的材质,电机泵盖通常使用铸铁、不锈钢、合金钢等金属材质,因此这类保持的硬度较高,一般会选择功率、扭矩较大的德国进口高精度主轴Kasite 4060 ER-S。 Kasite 4060 ER-…...

Android init.rc各阶段的定义和功能
Android开机优化系列文档-CSDN博客 Android 14 开机时间优化措施汇总-CSDN博客Android 14 开机时间优化措施-CSDN博客根据systrace报告优化系统时需要关注的指标和优化策略-CSDN博客Android系统上常见的性能优化工具-CSDN博客Android上如何使用perfetto分析systrace-CSDN博客A…...
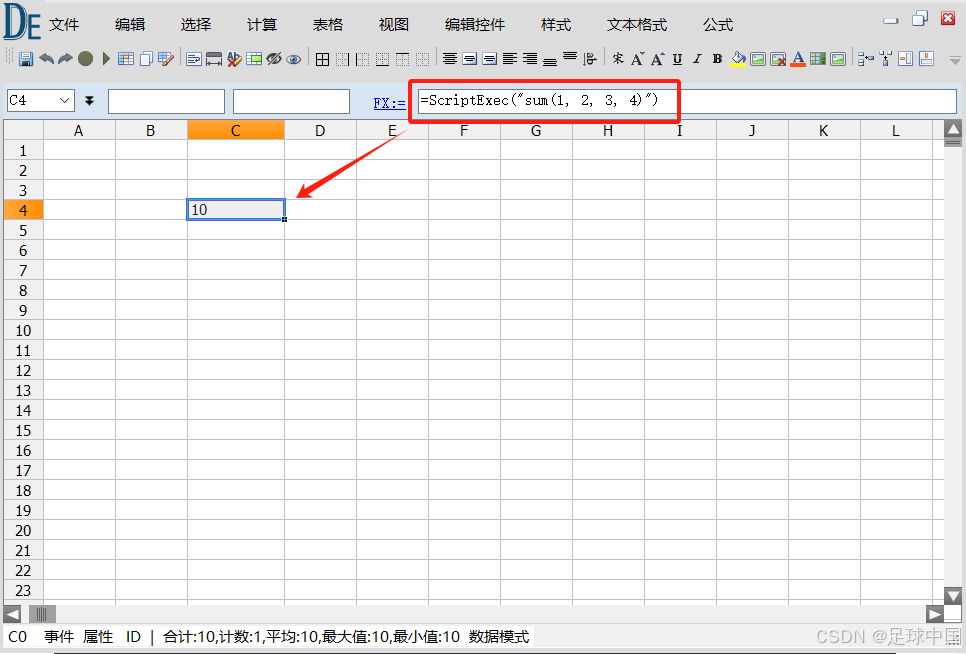
.net dataexcel 脚本公式 函数源码
示例如: ScriptExec(""sum(1, 2, 3, 4)"") 结果等于10 using Feng.Excel.Builder; using Feng.Excel.Collections; using Feng.Excel.Interfaces; using Feng.Script.CBEexpress; using Feng.Script.Method; using System; using System.Collections.Gen…...
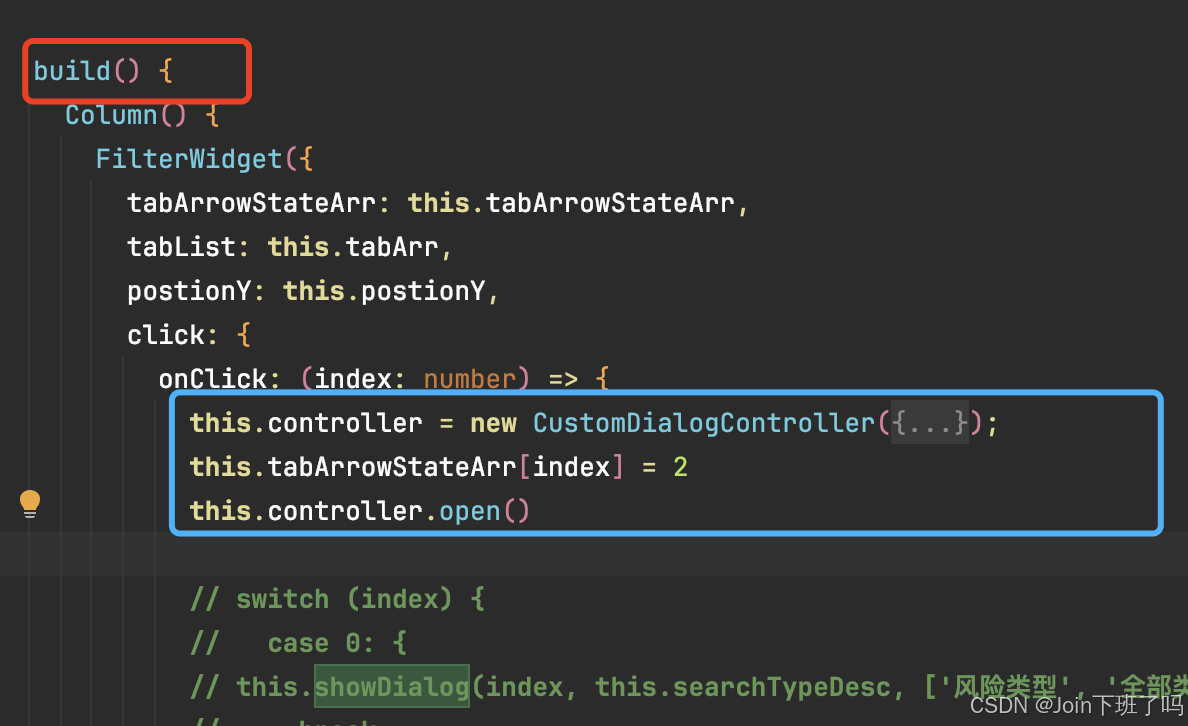
HarmonyOS ArkUi @CustomDialog 和promptAction.openCustomDialog踩坑以及如何选择
CustomDialog 内使用Link,如何正常使用 错误使用方式: 定义一个函数,在函数内使用弹窗,如下面代码showDialog: 这种使用方式,无法在自定义的CustomDialog内使用 Link,进行父子双向绑定&#x…...

Python面试题:详细讲解Python的多线程与多进程编程问题
在 Python 中,多线程和多进程编程是并发编程的两种主要方式,用于提高程序的执行效率和响应性。虽然它们都可以实现并发执行,但它们的工作原理和适用场景有所不同。以下是对 Python 多线程和多进程编程的详细讲解,包括它们的工作原…...
前端Canvas入门——用canvas写五子棋?
前言 五子棋的实现其实不难,因为本身就是一个很小的游戏。 至于画线什么的,其实很简单,都是lineTo(),moveTo()就行了。 难的在于——怎么让棋子落入到指定的格子上,怎么判断连子胜利。 当然啦,这部分是…...

[PaddlePaddle飞桨] PaddleDetection-通用目标检测-小模型部署
PaddleDetection的GitHub项目地址 推荐环境: PaddlePaddle > 2.3.2 OS 64位操作系统 Python 3(3.5.1/3.6/3.7/3.8/3.9/3.10),64位版本 pip/pip3(9.0.1),64位版本 CUDA > 10.2 cuDNN > 7.6pip下载指令: python -m pip i…...

Golang | Leetcode Golang题解之第239题滑动窗口最大值
题目: 题解: func maxSlidingWindow(nums []int, k int) []int {n : len(nums)prefixMax : make([]int, n)suffixMax : make([]int, n)for i, v : range nums {if i%k 0 {prefixMax[i] v} else {prefixMax[i] max(prefixMax[i-1], v)}}for i : n - 1…...

深度解析:在 React 中实现类似 Vue 的 KeepAlive 组件
在前端开发中,Vue 的 keep-alive 组件是一个非常强大的工具,它可以在组件切换时缓存组件的状态,避免重新渲染,从而提升性能。那么,如何在 React 中实现类似的功能呢?本文将带你深入探讨,并通过代…...

2024-7-20 IT新闻
目录 微软全球IT系统故障 中国量子计算产业峰会召开 其他IT相关动态 微软全球IT系统故障 后续处理: 微软和CrowdStrike均迅速响应,发布了相关声明并部署了修复程序。CrowdStrike撤销了有问题的软件更新,以帮助用户恢复系统正常运作。微软也…...
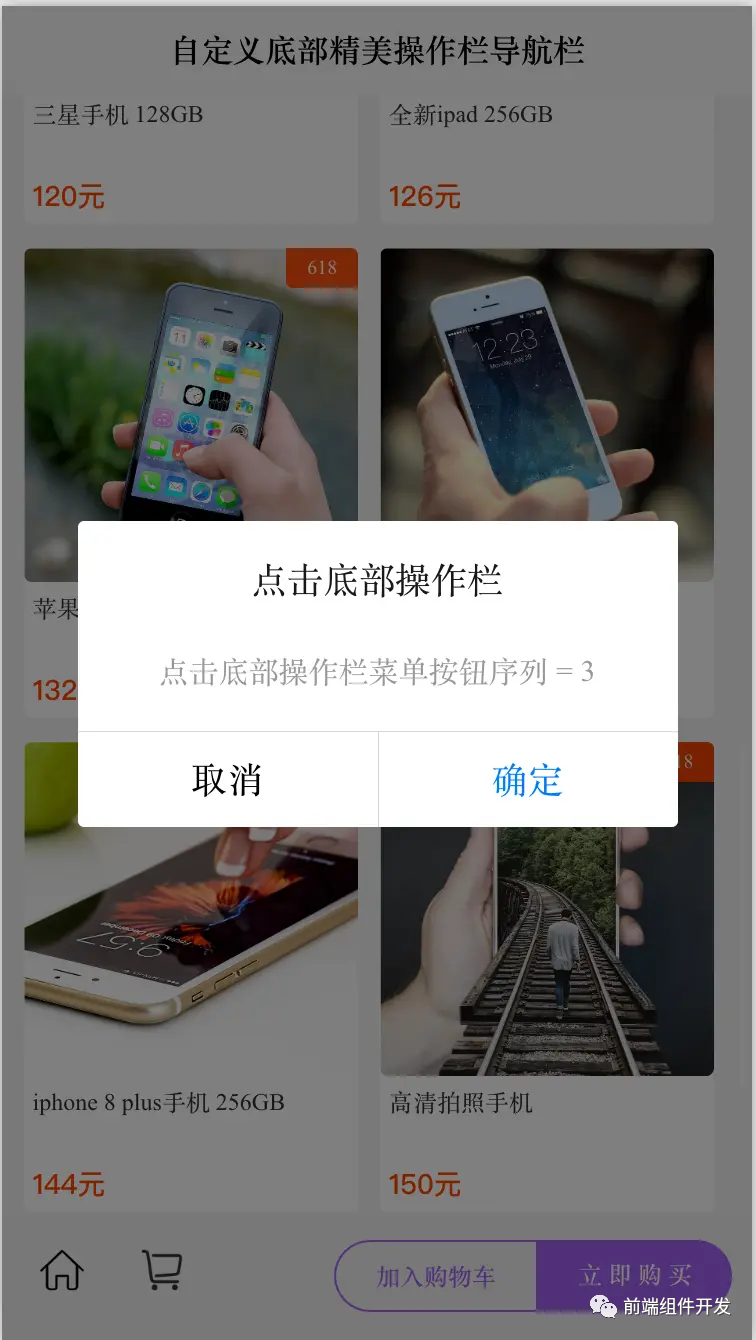
前端组件化开发:以Vue自定义底部操作栏组件为例
摘要 随着前端技术的不断演进,组件化开发逐渐成为提升前端开发效率和代码可维护性的关键手段。本文将通过介绍一款Vue自定义的底部操作栏组件,探讨前端组件化开发的重要性、实践过程及其带来的优势。 一、引言 随着Web应用的日益复杂,传统的…...

11.斑马纹列表 为没有文本的链接设置样式
斑马纹列表 创建一个背景色交替的条纹列表。 使用 :nth-child(odd) 或 :nth-child(even) 伪类选择器,根据元素在一组兄弟元素中的位置,对匹配的元素应用不同的 background-color。 💡 提示:你可以用它对其他 HTML 元素应用不同的样式,如 <div>、<tr>、<p&g…...

【算法】跳跃游戏II
难度:中等 题目: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[…...
学习大数据DAY20 Linux环境配置与Linux基本指令
目录 Linux 介绍 Linux 发行版 Linux 和 Windows 比较 Linux 就业方向: 下载 CentOS Linux 目录树 Linux 目录结构 作业 1 常用命令分类 文件目录类 作业 2 vim 编辑文件 作业 3 你问我第 19 天去哪了?第 19 天在汇报第一阶段的知识总结,没什…...

达梦+flowable改造
原项目springbootflowablemysql模式现需改造springbootflowable达梦, 1.在项目中引入达梦jpa包 引入高版本包已兼容flowable(6.4.2)liquibase(3.6.2) 我没有像网上做覆盖及达梦配置 <dependency> …...

【乐吾乐2D可视化组态编辑器】消息
消息 乐吾乐2D可视化组态编辑器demo:https://2d.le5le.com/ 监听消息 const fn (event, data) > {}; meta2d.on(event, fn);// 监听全部消息 meta2d.on(*, fn);// 取消监听 meta2d.off(event, fn); meta2d.off(*, fn); Copy 系统消息 event(…...
Qt创建列表,通过外部按钮控制列表的选中下移、上移以及左侧图标的显现
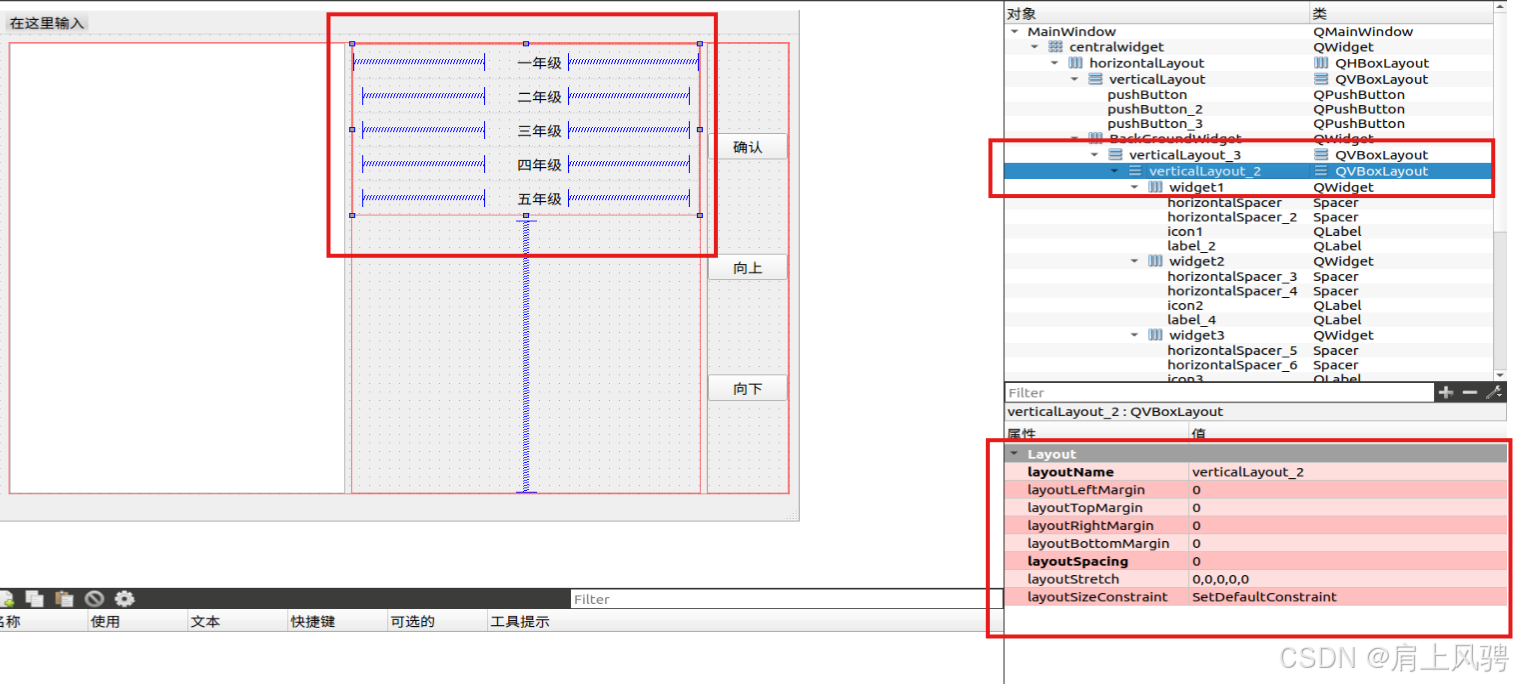
引言 项目中需要使用列表QListWidget,但是不能直接拿来使用。需要创建一个列表,通过向上和向下的按钮来向上或者向下移动选中列表项,当当前项背选中再去点击确认按钮,会在列表项的前面出现一个图标。 实现效果 本实例实现的效果如下: 实现思路 思路一 直接采用QLis…...

svn不能记住密码,反复弹出GNOME,自动重置svn.simple文件
1. 修改文件 打开 ~/.subversion/auth/svn.simple/xxx 更新前 K 15 svn:realmstring V 32 xxxxx //svn 地址,库的地址 K 8 username V 4 xxx //用户名 END在顶部插入下面内容, 注意,如果密码不对,则文件文法正常生效 更新后…...
对称加密与非对称加密
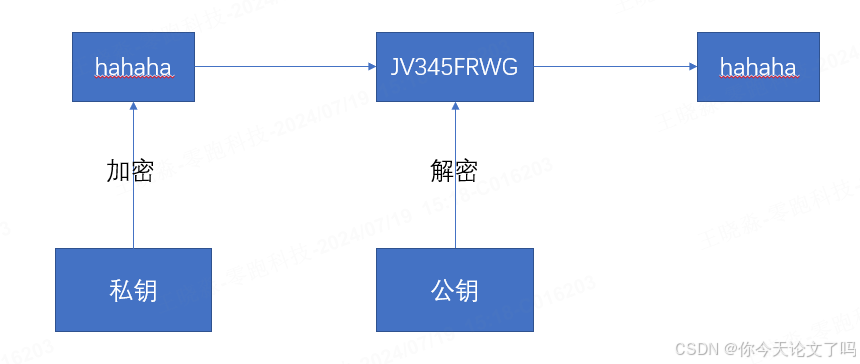
对称加密 对称加密指的是加密和解密使用同一个秘钥,所以叫对称加密。对称加密只有一个秘钥,称为私钥。 优点:算法公开、计算量小、加密速度快、效率高 缺点:数据传输前,发送方和接收方必须确定好秘钥,双方也必须要保存好秘钥。 常见对称加密算法: DES、3DES、AES、3…...

03 Git的基本使用
第3章:Git的基本使用 一、创建版本仓库 一)TortoiseGit 选择项目地址,右键,创建版本库 初始化git init版本库 查看是否生成.git文件(隐藏文件) 二)Git 选择项目地址,…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
