数据结构(稀疏数组)
简介
稀疏数组是一种数据结构,用于有效地存储和处理那些大多数元素都是零或者重复值的数组。在稀疏数组中,只有非零或非重复的元素会被存储,从而节省内存空间。
案例引入
假如想把下面这张表存入文件,我们会怎么做?

如果我们不做优化其实是浪费了很大一部分空间去存储空值,有没有办法既能实现效果又能节省空间呢?其实有的,稀疏数组就可以做到。

假如我们只存储右边的数据,相对左边做了相对大的数据压缩,会把空数据也就是无效的数据过滤,只存储有效的数据。
稀疏数组结构解释:
[0][0] - 记录原二维数组有几行
[0][1] - 记录原二维数组有几列
[0][2] - 记录原二维数组有多少个有效的数据
后面的一次记录有效数据所在行和列及有效数据的具体值
1,我们先将上图中的第一个数据结构转成程序中的二维数组
//1,将棋盘中的1,2用二维数组保存起来int[][] chessArray = new int[11][11];chessArray[1][2] = 1;chessArray[2][3] = 2;System.out.println("将棋盘转换为原始的二维数组");for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {System.out.printf("%d\t", chessArray[i][j]);}System.out.println();}
//2,将棋盘chessArray转出稀疏数组//稀疏数组一共有 row 3 col sum+1 第一行第一列未i行,第一行第二列为j列,第三个为num有效数据//第一步先要找出上述棋盘一共有多少个有效数据,计为sumint sum = 0;//默认0个有效数据for (int[] row : chessArray) {for (int data : row) {if (data != 0) {sum++;}}}//转换的稀疏数组int[][] sparseArray = new int[sum + 1][3];//将有效数据保存到稀疏数组中sparseArray[0][0] = chessArray.length;sparseArray[0][1] = chessArray.length;sparseArray[0][2] = sum;int count = 0;for(int i = 0;i<chessArray.length;i++){for(int j = 0 ;j<chessArray.length;j++){if(chessArray[i][j]!=0){count++;sparseArray[count][0] = i;sparseArray[count][1] = j;sparseArray[count][2] = chessArray[i][j];}}}System.out.println("转换的稀疏数组为");for(int []rows : sparseArray){for(int data:rows){System.out.printf("%d\t",data);}System.out.println();}
//将稀疏数组转出原始数组//1,读取第一行创建原始数组的大小int [][] chessArray2 = new int[sparseArray[0][0]][sparseArray[0][1]];System.out.println();System.out.println("原始数组"+sparseArray[0][0]+" "+sparseArray[0][1]);for(int i = 1;i<sparseArray.length;i++){chessArray2[sparseArray[i][0]][sparseArray[i][1]] = sparseArray[i][2];}System.out.println("转换的原始数组");for(int []rows : chessArray2){for(int data:rows){System.out.printf("%d\t",data);}System.out.println();}
总结
从上面的案例中,我们能感受到稀疏数组的一些特点:
存储效率:由于只存储非零或非重复的元素,稀疏数组在处理大量零值或重复值的数据时非常高效。
空间优化:相比于传统的数组,稀疏数组可以显著减少所需的存储空间。
稀疏性:稀疏数组中的元素大部分是零或重复值,这些值不需要存储。
实现方式:稀疏数组可以通过多种方式实现,例如使用哈希表、链表、位图或压缩存储等。
适用场景:稀疏数组适用于那些元素值重复或为零的情况,例如图的邻接矩阵、大规模数据集、科学计算中的矩阵等。
访问速度:虽然稀疏数组在存储上很高效,但访问速度可能会比传统数组慢,因为需要额外的查找步骤来定位非零元素。
更新和删除:在稀疏数组中更新或删除元素可能比在传统数组中更复杂,因为需要维护非零元素的索引或映射。
稀疏度:稀疏数组的效率很大程度上取决于其稀疏度,即非零或非重复元素占总元素的比例。稀疏度越高,稀疏数组的优势越明显。
总的来说,稀疏数组是一种针对特定数据特性优化的数据结构,可以在特定场景下提供存储和处理上的优势。
相关文章:

数据结构(稀疏数组)
简介 稀疏数组是一种数据结构,用于有效地存储和处理那些大多数元素都是零或者重复值的数组。在稀疏数组中,只有非零或非重复的元素会被存储,从而节省内存空间。 案例引入 假如想把下面这张表存入文件,我们会怎么做?…...

python 爬虫技术 第02节 基础复习
Python基础复习 Python 是一种高级、通用、解释型的编程语言,以其简洁的语法和强大的功能在数据科学、Web 开发、自动化脚本编写、机器学习等领域广泛使用。下面是一些 Python 基础概念的复习: 1. 数据类型 Python 支持多种内置数据类型,包…...

数据结构-C语言-排序(3)
代码位置:test-c-2024: 对C语言习题代码的练习 (gitee.com) 一、前言: 1.1-排序定义: 排序就是将一组杂乱无章的数据按照一定的规律(升序或降序)组织起来。(注:我们这里的排序采用的都为升序) 1.2-排序分…...

【分布式事务】怎么解决分布式场景下数据一致性问题
分布式事务的由来 拿充值订单举个栗子吧,假设:原本订单模块和账户模块是放在一起的,现在需要做服务拆分,拆分成订单服务,账户余额服务。原本收到充值回调后,可以将修改订单状态和扣减余额放在一个mysql事务…...

C# 中的委托
委托的概念 在C#中,委托是一种引用类型,它表示对方法的引用,即委托就是一种用来指向一个方法的引用类型变量。委托的声明类似于方法签名,但是关键字是delegate。下面是一个委托的声明和使用的例子: // 声明一个委托 p…...

通过docker构建基于LNMP的WordPress项目
目录 1.准备nginx 2.准备mysql 3.准备php 4.构建各镜像 5.运行wordpress 1、项目环境: 1.1 (1)公司在实际的生产环境中,需要使用Docker 技术在一台主机上创建LNMP服务并运行Wordpress网站平台。然后对此服务进行相关的性能…...

2024新版IntelliJ IDEA修改包名 全网最简单最粗暴的方法
问题再现 我们在网上淘一些后端框架 又或者是开源的项目 如果要变成自己的 难免会去改包名 即把com.后面的内容改成自己自定义的 第一次我们直接用网络上的方法 shift F6 快捷键 可以修改包名 出现以下情况 进行修改 我们发现失败了 并没有像预计的一样直接把包名修…...

C#中处理Socket粘包
在C#中使用Socket进行网络通信时,粘包问题是常见的。粘包问题通常发生在TCP协议中,因为TCP是流式协议,数据可能会被分割成多个包发送,也可能多个小包会被合并成一个大包接收。 处理粘包问题的常见方法是使用消息分隔符或消息长度…...

7.19IO
思维导图 第一题:测试错误检查锁和递归锁是否会造成死锁状态 #include <stdio.h> #include <string.h> #include <stdlib.h> #include <unistd.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #i…...

【Vue】深入了解 Axios 在 Vue 中的使用:从基本操作到高级用法的全面指南
文章目录 一、Axios 简介与安装1. 什么是 Axios?2. 安装 Axios 二、在 Vue 组件中使用 Axios1. 发送 GET 请求2. 发送 POST 请求 三、Axios 拦截器1. 请求拦截器2. 响应拦截器 四、错误处理五、与 Vuex 结合使用1. 在 Vuex 中定义 actions2. 在组件中调用 Vuex acti…...
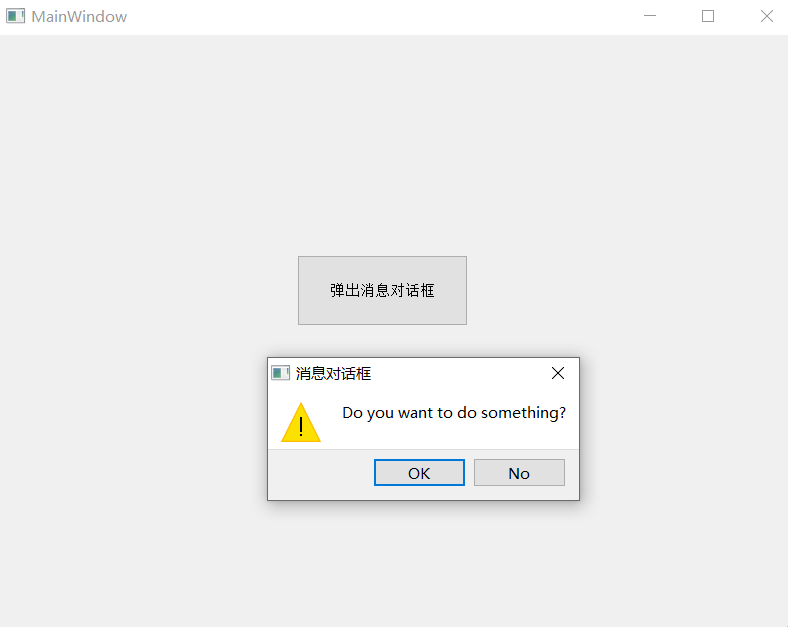
【Qt】窗口
文章目录 QMainWindow菜单栏工具栏状态栏浮动窗口对话框自定义对话框Qt内置对话框QMessageBox QMainWindow Qt中的主窗口以QMainWindow表示,其总体结构如下: 菜单栏 菜单栏MenuBar,可包含多个菜单Menu,每个菜单也可以包含多个菜…...

代码随想录训练营【贪心算法篇】
贪心 注:本文代码来自于代码随想录 贪心算法一般分为如下四步: 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步…...

Spark中的JOIN机制
Spark中的JOIN机制 1、Hash Join概述2、影响JOIN的因素3、Spark中的JOIN机制3.1、Shuffle Hash Join3.2、Broadcast Hash Join3.3、Sort Merge Join3.4、Cartesian Product Join3.5、Broadcast Nested Loop Join4、Spark中的JOIN策略5、Spark JOIN机制与策略总结5.1、Spark中的…...

WebRTC QOS方法十三.1(TimestampExtrapolator接收时间预估)
一、背景介绍 虽然我们可通过时间戳的差值和采样率计算出发送端视频帧的发送节奏,但是由于网络延迟、抖动、丢包,仅知道视频发送端的发送节奏是明显不够的。我们还需要评估出视频接收端的视频帧的接收节奏,然后进行适当平滑,保证…...

深入了解 GCC
GCC,全称 GNU Compiler Collection,是 GNU 项目的一部分,是一个功能强大且广泛使用的编译器套件。它支持多种编程语言,包括 C、C、Fortran、Java、Ada 和 Go。GCC 具有高度的可移植性,几乎可以在所有现代计算机体系结构…...

vscode 打开远程bug vscode Failed to parse remote port from server output
vscode 打开远程bug vscode Failed to parse remote port from server output 原因如图: 解决:...
前端组件化技术实践:Vue自定义顶部导航栏组件的探索
摘要 随着前端技术的飞速发展,组件化开发已成为提高开发效率、降低维护成本的关键手段。本文将以Vue自定义顶部导航栏组件为例,深入探讨前端组件化开发的实践过程、优势以及面临的挑战,旨在为广大前端开发者提供有价值的参考和启示。 一、引…...

PyTorch Autograd内部实现
原文: 克補 爆炸篇 25s (youtube.com) 必应视频 (bing.com)https://www.bing.com/videos/riverview/relatedvideo?&qPyTorchautograd&qpvtPyTorchautograd&mid1B8AD76943EFADD541E01B8AD76943EFADD541E0&&FORMVRDGAR 前面只要有一个node的re…...

微信小程序 vant-weapp的 SwipeCell 滑动单元格 van-swipe-cell 滑动单元格不显示 和 样式问题 滑动后删除样式不显示
在微信小程序开发过程中 遇到个坑 此处引用 swipeCell 组件 刚开始是组件不显示 然后又遇到样式不生效 首先排除问题 是否在.json文件中引入了组件 {"usingComponents": {"van-swipe-cell": "vant/weapp/swipe-cell/index","van-cell-gro…...

3.4、matlab实现SGM/BM/SAD立体匹配算法计算视差图
1、matlab实现SGM/BM/SAD立体匹配算法计算视差图简介 SGM(Semi-Global Matching)、BM(Block Matching)和SAD(Sum of Absolute Differences)都是用于计算立体匹配(Stereo Matching)的…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
