详解数据结构之二叉树(堆)
详解数据结构之二叉树(堆)
树
树的概念
- 树是一个非线性结构的数据结构,它是由 n(n>=0)个有限节点组成的一个具有层次关系的集合,它的外观形似一颗倒挂着的树,根朝上,叶朝下,所以称呼为树。每颗子树的根节点有且只有一个前驱,可以0个有多个后继。

如图:这两颗树就不是树形结构,子树是不会相交的,除根节点外每个节点有且只有一个父节点,一颗有n个节点的树有n - 1条边。

-
根节点
- 根节点没有前驱节点,如图:9为根节点。
-
父节点:若一个节点含有子节点,则称这个节点为字节的的父节点,如图9为12个父节点。
-
子节点/孩子节点:一个节点含有父节点那这个节点就为孩子节点,如图12.
-
节点的度:一个节点右多少个孩子节点那他的度就为多少。
- 树的度,为最大节点的度,如上图,12这个节点的度为3,它是最大的,那他就为树的度。
-
树的层次:从根开始定义为第一层,根节点的子节点为第二层,以此类推。
-
树的深度、高度:树的最大层次,如图,树最大有4层,那树的深度为4。
-
叶子节点:度为0的节点为叶子节点。
-
分支节点:度不为0的节点。
-
兄弟节点:具有相同父节点的节点互称为兄弟节点。
-
节点的祖先:从根到该结点所经分⽀上的所有结点
- 所有节点的祖先为根节点
-
节点的子孙:以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙
- 除根节点外所有节点是根节点的子孙。
-
森林:由m颗不相加的树的集合(m > 0)。
二叉树
在树形结构里最常用的就是二叉树,一颗二叉树是节点的有限集合,该集合右一个根节点加上两颗左子树和右字树组成或者为空。
二叉树形态:
- 空二叉树
- 只有一个根节点
- 根节点只有左子树
- 根节点只有右子树
- 根节点有左右子树
二叉树的特点:
- 二叉树不存在度大于2的节点
- 二叉树的节点有左右之分,次序不能颠倒,而二叉树又是有序树
特殊二叉树:
满二叉树是节点总数满足 2^k - 1(k为树的最大层数)的树,每一层的节点个数都达到最大值。

完全二叉树:对于一颗具有n个节点的二叉树按层序编号,如果编号为i(1 <= i <= n)的节点与同样深度的满二叉树中编号为i的节点在二叉树中的位置完全相同,这颗二叉树称为完全二叉树。
例如:
序号为2的节点没有右节点而序号为3的节点先有了序号为5、6的节点此时它们的序号与上图的完全二叉树序号并不相同,那它就不是完全二叉树。

正确的完全二叉树:

判断完全二叉树时,可以先按照当前二叉树的层次画一个或着心里想一个满二叉树,判断对应位置上的序号大小是否一致。
完全二叉树的性质:
- 叶子节点只能出现在最后两层
- 最下层的叶子节点一定集中在左部连续的位置
- 倒数第二层有叶子节点那他一定在右部连续位置
二叉树的性质
二叉树总节点个数:深度为k的二叉树具有,n = 2^k - 1个节点
二叉树第i层的节点个数:第i层的节点有,2^(i-1) 个。
对应具有n个节点个数的二叉树对应的深度为:k = logn + 1,底数为2
堆
堆,将一个元素集合k里,所有数据按照完成二叉树的存储方式存储。
这里的堆是基于顺序存储结构实现,因为堆是一种要求严格的二叉树,在节点的顺序上,必须是从左孩子节点开始放数据,不会允许一个节点先有右孩子节点,而没有左孩子节点。
有了这种特殊的限制,在数组里就可以利用节点所对应的下标来寻找对于的父亲节点,孩子节点。‘
对于具有 n 个结点的完全⼆叉树,如果按照从上到下从左到右的数组顺序对所有结点从 0 开始编号,则对于序号为 i 的结点有:
i > 0 ,i 位置的节点的双亲序号为:(i - 1) / 2,i = 0 为根节点为双亲。
若 2i + 1 < n,左孩子序号:2i + 1,否则2i + 1>= n无左孩子
若 2i + 2 < n,右孩子序号:2i + 2,否则2i + 2>= n无右孩子
堆的分类:
-
小根堆(小堆),父亲节点的大小总是小于孩子节点

-
大根堆(大堆),父亲节点的大小总是大于孩子节点
不满足以上两种的堆是无序的无效的堆,必须对其的循序进行调整。
typedef int HeapDataType;
typedef struct Heap
{HeapDataType* arr;int size;int capacity;
}Heap;
功能实现
//初始化
void HpInit(Heap* hp);
//销毁
void HpDestory(Heap* hp);
//堆尾放数据
void HpPush(Heap* hp, HeapDataType x);
//出堆顶数据
void HpPop(Heap* hp);
//自下向上调整
void AdjustUp(HeapDataType* arr, int child);
//自上向下调整
void AdjustDown(HeapDataType* arr, int parent, int n);
//返回堆顶数据
HeapDataType HeapTop(Heap* hp);
//返回堆的数据个数
int HeapSize(Heap* hp);
//交换函数Swap
void Swap(HeapDataType* x, HeapDataType* y);
初始化、销毁
初始化:基于顺序结构实现的堆,将指向堆的变量的地址传递过来使用一级指针接收,实现形参的改变影响到实参。初始化堆,只需对其指针置空、空间大小和栈顶置0即可。
void HpInit(Heap* hp)
{assert(hp);if(hp->arr)free(hp->arr);hp->arr = NULL;hp->capacity = hp->size = 0;
}
销毁堆:堆的空间是使用函数动态开辟的,那他得使用对应得free对空间进行释放,让后将堆的空间大小和,size置0即可。
需要注意的是若数组本身是空的那就不能对齐进行释放,在使用free释放前还需要使用if语句进行判断。是否为空。
void HpDestory(Heap* hp)
{assert(hp);if (hp->arr)free(hp->arr);hp->capacity = hp->size = 0;
}
堆插入数据、自下向上调整算法
在堆里插入数据有着严格的要求,必须按照这从左节点到右节点的顺序放入数据,不能跳过左节点,先放入右节点的数据。

现在想要在堆里放入一个数据,不能是我想在哪放就在哪放的,必须先将节点20的右孩子节点放入数据,才能到下一层放入数据。这些严格的要求也导致了用数组实现堆,存放数据也是从末尾开始。
而前文说过,堆是按照一定顺序存放的,在如图的小堆里,我放入了一个10的数据,改如何应对呢?这里就得使用到堆的自下向上调整函数,其函数功能是将堆里新放入的数据按照小堆的结构摆放。
堆插入数据
在堆里放入数据只需在数组末尾存放即可。
需要注意的是,对空间大小的判断,以及自下向上调整算法。
在函数里,需要对有效数据个数和空间大小是否相等进行判断,所以使用if语句,在if语句里,使用realloc函数开辟,为啥不使用malloc函数呢~,我们需要实现的动态开辟,存放的数据越多,空间越开越大,malloc函数做不到。扩容时需扩容原空间的2倍或3倍可以减少扩容操作的频率。如果每次只增加少量空间,那么在元素数量增长时,需要频繁进行扩容操作,这会降低性能。
在完成对空间大小的判断与开辟后,将待插入数据放入数组末尾即可。然后使用自下向上调整算法对新放入的数据根据大小调整顺序。
void HpPush(Heap* hp, HeapDataType x)
{assert(hp);if (hp->capacity == hp->size){int newcapacity = hp->arr == 0 ? 4 : hp->capacity * 2;HeapDataType* newarr = (HeapDataType*)realloc(hp->arr, sizeof(HeapDataType) * newcapacity);if (newarr == NULL){perror("malloc ");exit(1);}hp->arr = newarr;hp->capacity = newcapacity;}hp->arr[hp->size] = x;AdjustUp(hp->arr, hp->size);hp->size++;//交换完在进行加加,提前加加hp->arr[hp->size++] = x;然后在调整会有越界情况
}
自下向上调整算法
这里将交换两个数据的功能封装为一个函数,后续实现出堆顶数据还需要使用它。
void Swap(HeapDataType* x, HeapDataType* y)
{HeapDataType temp = *x;*x = *y;*y = temp;
}
计算父亲节点的大小:父亲 = (孩子 - 1) / 2。
自下向上算法的实现基于二叉树的性质,更具孩子节点找父亲节点。新插入的孩子节点需要与父亲节点进行比较大小,若孩子节点小于父亲节点就交换顺序,而新的父亲节点又是前一个节点的孩子节点,同样需要判断其大小,然后交换顺序,若父亲节点小于孩子节点的话就不需要继续循环下去使用break跳出。
循环结束的条件:当child不大于0时跳出,若child都小于0了还怎么访问堆里的数据,而child刚好为0的说明此时孩子指的是根节点,根节点并不需要交换,所以child不大于0时跳出即可。
从孩子开始为堆的最后一个数据,所以称为自下向上调整。
void AdjustUp(HeapDataType* arr, int child)//传递数组和数组的大小,也就是插入数据的位置
{int parent = (child - 1) / 2;while (child > 0){//小堆:<//大堆:>if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);//交换child = parent;//交换完后更新孩子节点的位置。parent = (child - 1) / 2;//跟新父亲节点的位置,为新孩子节点的父亲节点。}else{break;}}
}
建大堆
若我们需要一个大堆,这里只需要改变if语句里的条件判断,将找更小的逻辑改为找更大的数据即可。
出堆顶数据、自上向下调整算法
出堆顶数据也有严格的要求,并不是将数组末尾的数据删除,直接将size减1,也不是让数组所有数据前移一位,这将会到的堆的顺序全部乱套了~坏掉了!
出堆顶数据
出堆顶数据是将堆顶的数据与堆尾的数据进行交换,然后让size减1(堆的数据个数),最后将新的堆顶数据按照小堆的摆放调整顺序。
出堆顶数据时需要注意,堆不能为空,以及数组也不能为空否则将会做坏事,导致统子哥报错。
void HpPop(Heap* hp)
{assert(hp && hp->size);Swap(&hp->arr[0], &hp->arr[hp->size - 1]);//将最后一个元素与堆顶元素交换hp->size--;//调整顺序AdjustDown(hp->arr, 0, hp->size);
}
自上向下调整算法
左孩子:孩子 = 父亲 * 2 + 1,child < n
右孩子:孩子 = 父亲 * 2 + 2,child < n
前文提过的自下向上调整算法是向上找父亲节点,而自上向下算法是向下找孩子节点更具传递过来的参数 parent 向下个找孩子。
与前一个调整算法相比,它会进行更多的判断,因为向下找的孩子有两个。而我们默认的孩子起始是左孩子节点。
在对孩子节点与父亲节点比较大小交换之前还需要比较左孩子节点和右孩子节点,arr[child] > arr[child + 1],若左孩子节点大于有孩子,那child就需要加1,但还有个前提,万一child加1后刚好不满足 child < n的条件从而在后续的交换里导致数组越界访问,所以在if语句里还需要加上一条判断 child + 1 < n。
执行孩子节点与父亲节点交换的if语句里,在交换完两个节点后需要更新新的父亲节点,和孩子节点来是否存在比父亲节点还小的值。最后若孩子节点大于父亲节点,那就说明不需要交换,使用break跳出循环即可。
void AdjustDown(HeapDataType* arr, int parent, int n)
{int child = parent * 2 + 1;while (child < n){//小堆:>//大堆:<if (child + 1 < n && arr[child] > arr[child + 1]){child++;}//小堆:<//大堆:>if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
建大堆
若我们需要一个大堆,那该如何调整,这里只需要改变其两个if语句里的条件判断,将找更小的逻辑改为找更大的数据即可。
返回堆顶数据
将数组下标为零的元素返回,即是堆顶。
HeapDataType HeapTop(Heap* hp)
{assert(hp && hp->size);return hp->arr[0];
}
返回堆的数据个数
将size的大小返回即是堆存储的数据个数。
int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}
源码
Heap.h
#pragma once#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>typedef int HeapDataType;
typedef struct Heap
{HeapDataType* arr;int size;int capacity;
}Heap;//初始化
void HpInit(Heap* hp);//销毁
void HpDestory(Heap* hp);//堆尾放数据
void HpPush(Heap* hp, HeapDataType x);
//出堆顶数据
void HpPop(Heap* hp);
//自下向上调整
void AdjustUp(HeapDataType* arr, int child);
//自上向下调整
void AdjustDown(HeapDataType* arr, int parent, int n);
//返回堆顶数据
HeapDataType HeapTop(Heap* hp);
//返回堆的数据个数
int HeapSize(Heap* hp);
//交换函数Swap
void Swap(HeapDataType* x, HeapDataType* y);
Heap.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"//初始化
void HpInit(Heap* hp)
{assert(hp);hp->arr = NULL;hp->capacity = hp->size = 0;
}//销毁
void HpDestory(Heap* hp)
{assert(hp);if (hp->arr)free(hp->arr);hp->capacity = hp->size = 0;
}
void Swap(HeapDataType* x, HeapDataType* y)
{HeapDataType temp = *x;*x = *y;*y = temp;
}
//自下向上调整
void AdjustUp(HeapDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//堆尾放数据
void HpPush(Heap* hp, HeapDataType x)
{assert(hp);if (hp->capacity == hp->size){int newcapacity = hp->arr == 0 ? 4 : hp->capacity * 2;HeapDataType* newarr = (HeapDataType*)realloc(hp->arr, sizeof(HeapDataType) * newcapacity);if (newarr == NULL){perror("malloc ");exit(1);}hp->arr = newarr;hp->capacity = newcapacity;}hp->arr[hp->size] = x;AdjustUp(hp->arr, hp->size);hp->size++;
}//自上向下调整
void AdjustDown(HeapDataType* arr, int parent, int n)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && arr[child] > arr[child + 1]){child++;}if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//出堆顶数据
void HpPop(Heap* hp)
{assert(hp && hp->size);Swap(&hp->arr[0], &hp->arr[hp->size - 1]);//将最后一个元素与堆顶元素交换hp->size--;//调整顺序AdjustDown(hp->arr, 0, hp->size);
}
//返回堆顶数据
HeapDataType HeapTop(Heap* hp)
{assert(hp && hp->size);return hp->arr[0];
}int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}}if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//出堆顶数据
void HpPop(Heap* hp)
{assert(hp && hp->size);Swap(&hp->arr[0], &hp->arr[hp->size - 1]);//将最后一个元素与堆顶元素交换hp->size--;//调整顺序AdjustDown(hp->arr, 0, hp->size);
}
//返回堆顶数据
HeapDataType HeapTop(Heap* hp)
{assert(hp && hp->size);return hp->arr[0];
}int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}
相关文章:

详解数据结构之二叉树(堆)
详解数据结构之二叉树(堆) 树 树的概念 树是一个非线性结构的数据结构,它是由 n(n>0)个有限节点组成的一个具有层次关系的集合,它的外观形似一颗倒挂着的树,根朝上,叶朝下,所以称呼为树。每颗子树的根节点有且只…...

Linux----Mplayer音视频库的移植
想要播放视频音乐就得移植相关库到板子上 Mplayer移植需要依赖以下源文件:(从官网获取或者网上) 1、zlib-1.2.3.tar.gz :通用的内存空间的压缩库。 2、libpng-1.2.57.tar.gz :png格式图片的压缩或解压库 3、Jpegsrc.v9b.tar.gz : jpeg格式图片的压…...

STM32测测速---编码电机读取速度的计算
1、首先先了解一下计算的公式 速度计算: 轮胎每转一圈的脉冲数取决于编码器的分辨率,可由下面公式进行计算: PPR是电机的线数 以GA25-370电机为例。 图片来源:第四节:STM32定时器(4.JGA25-370霍尔编码器…...

【已解决】服务器无法联网与更换镜像源
目录 问题描述: 1.修改网卡的 DNS1 和 DNS2 2.修改DNS列表 3.重启网络服务 4.切换镜像源 4.1备份原镜像源 4.2下载阿里云镜像源 4.3替换无法使用的域名 4.4刷新软件包缓存 4.5其他镜像源 5.阿里云镜像源开发者社区说明 6.阿里云DNS网址 7.DNS域名服务器…...

android11 屏蔽usb通过otg转接口外接鼠标设备
硬件平台:QCS6125 软件平台:Android11 需求:Android设备通过接usb转接线连接鼠标功能屏蔽。 考虑到屏蔽的层面可以从两个层面去做,一个是驱动层面不识别,一个就是Android系统层面不识别加载,本篇只讲后者。…...

HAL库源码移植与使用之RTC时钟
实时时钟(Real Time Clock,RTC),本质是一个计数器,计数频率常为秒,专门用来记录时间。 普通定时器无法掉电运行!但RTC可由VBAT备用电源供电,断电不断时 这里讲F1系列的RTC 可以产生三个中断信号ÿ…...

GIT命令学习 一
📑打牌 : da pai ge的个人主页 🌤️个人专栏 : da pai ge的博客专栏 ☁️宝剑锋从磨砺出,梅花香自苦寒来 ☁️运维工程师的职责:监…...

VS+QT 打包可执行文件.exe
切换成release版本,同时更改项目属性中release配置下的各个属性,确保匹配 重新生成解决方案,将生成的.exe复制到一个空白文件夹中 执行: cd D:\QT\5.12.10\msvc2015_64\binwindeployqt C:\Users\DELL\Desktop\serials\MainWind…...
)
Android笔试面试题AI答之Activity(2)
答案仅供参考,大部分为文心一言AI作答 目录 1. 请介绍一下Activity 生命周期?1. 完全生命周期2. 可见生命周期3. 前台生命周期4. 配置更改5. 特殊场景 2. 请介绍一下横竖屏切换时Activity的生命周期变化?1.默认行为(未设置androi…...
 通俗解释)
来自Transformers的双向编码器表示(BERT) 通俗解释
来自Transformers的双向编码器表示(BERT) 目录 1. 从上下文无关到上下文敏感2. 从特定于任务到不可知任务3. BERT:把两个最好的结合起来4. BERT的输入表示5. 掩蔽语言模型(Masked Language Modeling)6. 下一句预测&am…...
)
代码随想录第十六天|贪心算法(2)
目录 LeetCode 134. 加油站 LeetCode 135. 分发糖果 LeetCode 860. 柠檬水找零 LeetCode 406. 根据身高重建队列 LeetCode 452. 用最少数量的箭引爆气球 LeetCode 435. 无重叠区间 LeetCode 763. 划分字母区间 LeetCode 56. 合并区间 LeetCode 738. 单调递增的数字 总…...

花几千上万学习Java,真没必要!(二十二)
1、final关键字: 测试代码1: package finaltest.com;public class FinalBasicDemo {public static void main(String[] args) {// final修饰基本数据类型变量final int number 5;// 尝试修改number的值,这将导致编译错误// number 10; // …...

在RK3568上如何烧录MAC?
这里我们用RKDevInfoWriteTool 1.1.4版本 下载地址:https://pan.baidu.com/s/1Y5uNhkyn7D_CjdT98GrlWA?pwdhm30 提 取 码:hm30 烧录过程: 1. 解压RKDevInfoWriteTool_Setup_V1.4_210527.7z 进入解压目录,双击运行RKDevInfo…...
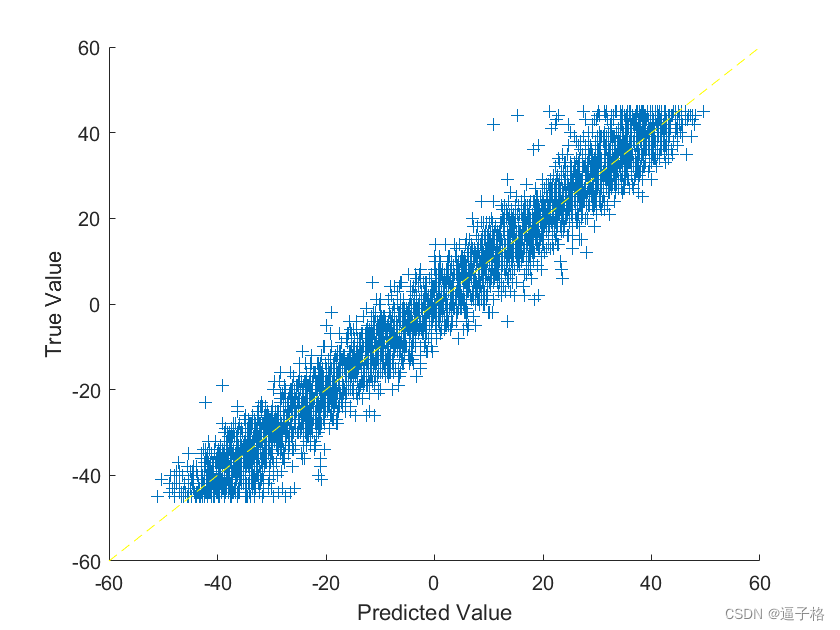
1.30、基于卷积神经网络的手写数字旋转角度预测(matlab)
1、卷积神经网络的手写数字旋转角度预测原理及流程 基于卷积神经网络的手写数字旋转角度预测是一个常见的计算机视觉问题。在这种情况下,我们可以通过构建一个卷积神经网络(Convolutional Neural Network,CNN)来实现该任务。以下…...

Windows如何使用Python的sphinx
在Windows上使用Python的Sphinx进行文档渲染和呈现,可以遵循以下步骤进行操作: 安装Python:首先,确保你的Windows系统上已经安装了Python。你可以从Python的官方网站下载并安装适合你系统(32位或64位&…...

C++ STL nth_element 用法
一:功能 将一个序列分为两组,前一组元素都小于*nth,后一组元素都大于*nth, 并且确保第 nth 个位置就是排序之后所处的位置。即该位置的元素是该序列中第nth小的数。 二:用法 #include <vector> #include <a…...

【PostgreSQL教程】PostgreSQL 选择数据库
博主介绍:✌全网粉丝20W+,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物联网、机器学习等设计与开发。 感兴趣的可…...

C# —— HashTable
集合collections命名空间,专门进行一系列的数据存储和检索的类,主要包含了:堆栈、和队列、list、ArrayList、数组 HashTable 字典 storeList 排序列表等类 Array 数组 长度固定, 类型固定 通过索引值来进行访问 ArrayList动态数组,…...

LeetCode 第407场周赛个人题解
目录 100372. 使两个整数相等的位更改次数 原题链接 思路分析 AC代码 100335. 字符串元音游戏 原题链接 思路分析 AC代码 100360. 将 1 移动到末尾的最大操作次数 原题链接 思路分析 AC代码 100329. 使数组等于目标数组所需的最少操作次数 原题链接 思路分析 A…...

使用Django框架实现音频上传功能
数据库设计(models.py) class Music(models.Model):""" 音乐 """name models.CharField(verbose_name"音乐名字", max_length32)singer models.CharField(verbose_name"歌手", max_length32)# 本质…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
