(前缀和) LeetCode 238. 除自身以外数组的乘积
一. 题目描述
原题链接
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums =[1,2,3,4]输出:[24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
二. 解题思路
本题意思是计算每一个nums[i]的值,其中nums[i] 的值为除自身以外的其他值的乘积。
首先我们定义两个数组 left 和 right ,其中 left 数组用来计算数组的前缀和,right 数组用来计算数组的后缀和,至于最终计算结果我们只需要在原数组上操作即可,省略了空间的浪费,nums[i] 的最终结果就等于nums[i - 1] 的前缀和乘 nums[i + 1] 的后缀和,即 nums[i] = left[i - 1] * right[i + 1]。
但是在计算nums[0] 和nums[n - 1] 的时候我们发现会出现数组越界错误,所以我们将 left 数组元素统一后移一位,然后将 left[0] 赋予 1,将 right 数组扩展一位,right[n] 赋予1 。所以就可以得出:nums[i] = left[i] * right[i + 1] (原本是 left[i - 1] * right[i + 1],但是 left 元素统一后移一位,所以下标也会移动,但是 right 数组只是扩展,对下标未改动);
运算过程如图所示:

三. 代码
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();int sum = 0;vector<int> left(n + 1);vector<int> right(n + 1);left[0] = 1;right[n] = 1;for(int i = 0; i < n; i++){left[i + 1] = nums[i] * left[i];}for(int i = n - 1; i >= 0; i--){right[i] = right[i + 1] * nums[i];}for(int i = 0; i < n; i++){nums[i] = left[i] * right[i + 1];}return nums;}
};四. 总结
本题属于前缀和和后缀和的集合考察,属于中等题目,大家可以练习一下,但是一定要考虑在左右位置计算的时候的越界问题。
时间复杂度:O(n);
空间复杂度:O(n);
爱思考的小伙伴可以想一下本题如何用O(1)的空间复杂度实现,欢迎评论!
喜欢的话给个关注吧!!
相关文章:

(前缀和) LeetCode 238. 除自身以外数组的乘积
一. 题目描述 原题链接 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法&…...

【JVM基础05】——组成-能不能解释一下方法区?
目录 1- 引言:方法区概述1-1 方法区是什么?(What)1-2 为什么用方法区?方法区的作用 (Why) 2- ⭐核心:详解方法区(How)2-1 能不能解释一下方法区?2-2 元空间内存溢出问题2-3 什么是常量池?2-4 运行时常量池 …...

前端:Vue学习-3
前端:Vue学习-3 1. 自定义指令2. 插槽2.1 插槽 - 后备内容(默认值)2.2 插槽 - 具名插槽2.3 插槽 - 作用域插槽 3. Vue - 路由3.1 路由模块封装3.2 声明式导航 router-link 高亮3.3 自定义匹配的类名3.4 声明式导肮 - 跳转传参3.5 Vue路由 - 重…...

npm 安装报错(已解决)+ 运行 “wue-cli-service”不是内部或外部命令,也不是可运行的程序(已解决)
首先先说一下我这个项目是3年前的一个项目了,中间也是经过了多个人的修改惨咋了布置多少个人的思想,这这道我手里直接npm都安装不上,在网上也查询了多种方法,终于是找到问题所在了 问题1: 先是npm i 报错在下面图片&…...
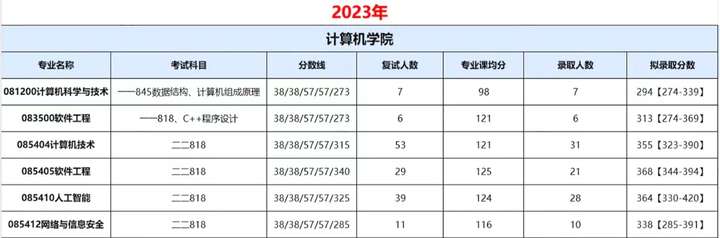
江苏科技大学24计算机考研数据速览,有专硕复试线大幅下降67分!
江苏科技大学(Jiangsu University of Science and Technology),坐落在江苏省镇江市,是江苏省重点建设高校,江苏省人民政府与中国船舶集团有限公司共建高校,国家国防科技工业局与江苏省人民政府共建高校 &am…...

20分钟上手新版Skywalking 9.x APM监控系统
Skywalking https://skywalking.apache.org/ Skywalking是专为微服务、云原生和基于容器的(Kubernetes)架构设计的分布式系统性能监控工具。 Skywalking关键特性 ● 分布式跟踪 ○ 端到端分布式跟踪。服务拓扑分析、以服务为中心的可观察性和API仪表板。…...

【07】LLaMA-Factory微调大模型——微调模型导出与微调参数分析
上文介绍了如何对微调后的模型进行使用与简单评估。本文将介绍对微调后的模型进行导出的过程。 一、llama-3微调后的模型导出 首先进入虚拟环境,打开LLaMA-Factory的webui页面 conda activate GLM cd LLaMA-Factory llamafactory-cli webui 之后,选择…...
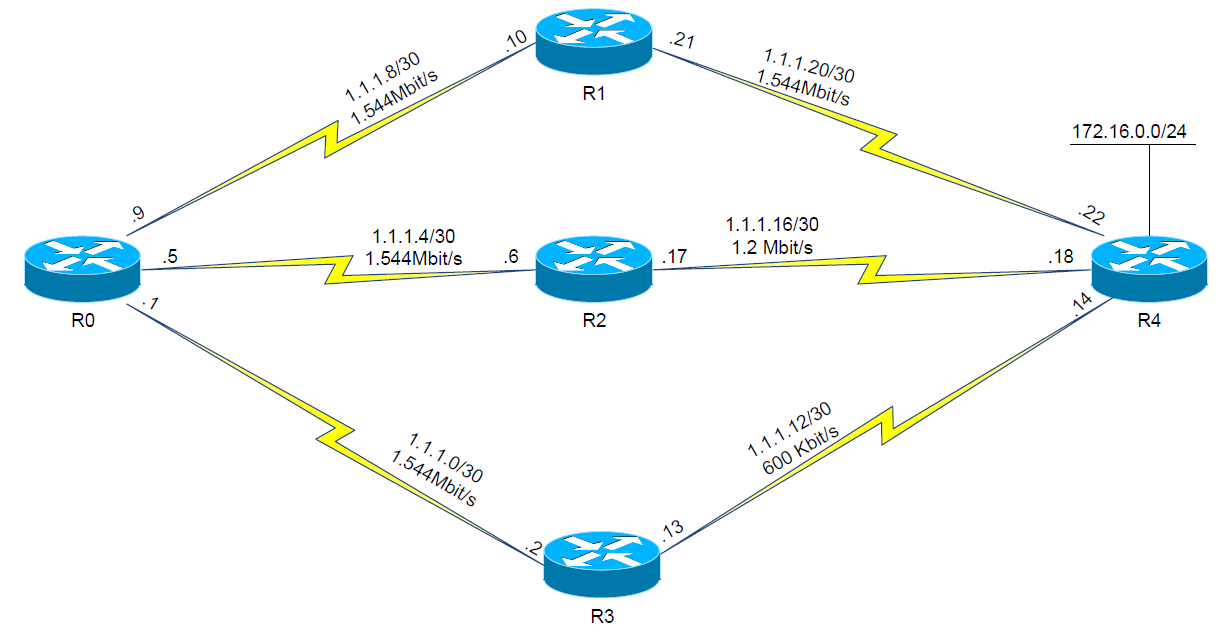
动态路由协议 —— EIGRP 与 OSPF 的区别
EIGRP(增强内部网关路由协议)和 OSPF(开放式最短路径优先)是两种最常见的动态路由协议,主要是用来指定路由器或交换机之间如何通信。将其应用于不同的情况下,可提高速率、延迟等方面的性能。那么它们之间到…...

【中项】系统集成项目管理工程师-第5章 软件工程-5.1软件工程定义与5.2软件需求
前言:系统集成项目管理工程师专业,现分享一些教材知识点。觉得文章还不错的喜欢点赞收藏的同时帮忙点点关注。 软考同样是国家人社部和工信部组织的国家级考试,全称为“全国计算机与软件专业技术资格(水平)考试”&…...

HarmonyOS应用开发者高级认证,Next版本发布后最新题库 - 多选题序号1
基础认证题库请移步:HarmonyOS应用开发者基础认证题库 注:有读者反馈,题库的代码块比较多,打开文章时会卡死。所以笔者将题库拆分,单选题20个为一组,多选题10个为一组,题库目录如下,…...

Windows11(24H2)LTSC长期版下载!提前曝光Build26100?
系统;windows11 文章目录 前言一、LTSC是什么?二、 Windows 11 Vision 24H2 LTSC 的版本号为 Build 26100,镜像中提供以下三个 SKU:总结 前言 好的系统也能给你带来不一样的效果。 一、LTSC是什么? & & L…...

【北京迅为】《i.MX8MM嵌入式Linux开发指南》-第三篇 嵌入式Linux驱动开发篇-第四十三章 驱动模块传参
i.MX8MM处理器采用了先进的14LPCFinFET工艺,提供更快的速度和更高的电源效率;四核Cortex-A53,单核Cortex-M4,多达五个内核 ,主频高达1.8GHz,2G DDR4内存、8G EMMC存储。千兆工业级以太网、MIPI-DSI、USB HOST、WIFI/BT…...

uniapp 小程序 支付逻辑处理
uniapp 小程序 支付逻辑处理 上代码如果你不需要支付宝适配,可以删除掉支付宝的条件判断代码 <button class"subBtn" :disabled"submiting" click"goPay">去支付</button>// 以下代码你需要改的地方// 1. order/app/v1…...

scikit-learn库学习之make_regression函数
scikit-learn库学习之make_regression函数 一、简介 make_regression是scikit-learn库中用于生成回归问题数据集的函数。它主要用于创建合成的回归数据集,以便在算法的开发和测试中使用。 二、语法和参数 sklearn.datasets.make_regression(n_samples100, n_feat…...
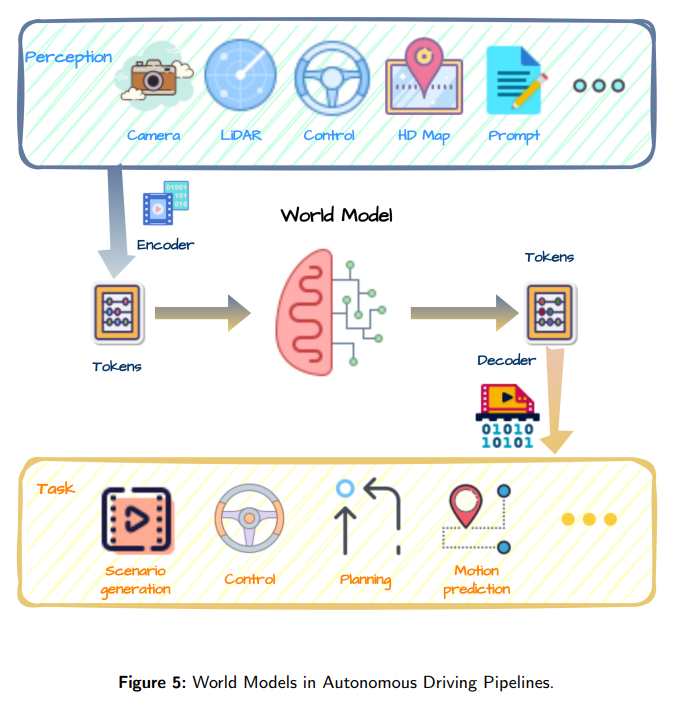
经典文献阅读之--World Models for Autonomous Driving(自动驾驶的世界模型:综述)
Tip: 如果你在进行深度学习、自动驾驶、模型推理、微调或AI绘画出图等任务,并且需要GPU资源,可以考虑使用UCloud云计算旗下的Compshare的GPU算力云平台。他们提供高性价比的4090 GPU,按时收费每卡2.6元,月卡只需要1.7元每小时&…...
)
孙健提到的实验室的研究方向之一是什么?()
孙健提到的实验室的研究方向之一是什么?() 点击查看答案 A.虚拟现实B.环境感知和理解 C.智能体博弈D.所有选项都正确 图灵奖是在哪一年设立的?() A.1962B.1966 C.1976D.1986 孙健代表的实验室的前身主要研究什么?&…...

初级java每日一道面试题-2024年7月23日-Iterator和ListIterator有什么区别?
面试官: Iterator和ListIterator有什么区别? 我回答: Iterator和ListIterator都是Java集合框架中用于遍历集合元素的接口,但它们之间存在一些关键的区别,主要体现在功能和使用场景上。下面我将详细解释这两种迭代器的不同之处: 1. Iterat…...

2024-07-23 Unity AI行为树2 —— 项目介绍
文章目录 1 项目介绍2 AI 代码介绍2.1 BTBaseNode / BTControlNode2.2 动作/条件节点2.3 选择 / 顺序节点 3 怪物实现4 其他功能5 UML 类图 项目借鉴 B 站唐老狮 2023年直播内容。 点击前往唐老狮 B 站主页。 1 项目介绍 本项目使用 Unity 2022.3.32f1c1,实现基…...

Unity-URP-SSAO记录
勾选After Opacity Unity-URP管线,本来又一个“bug”, 网上查不到很多关于ssao的资料 以为会不会又是一个极度少人用的东西 而且几乎都是要第三方替代 也完全没有SSAO大概的消耗是多少,完全是黑盒(因为用的人少,研究的人少,优…...

无人机上磁航技术详解
磁航技术,也被称为地磁导航,是一种利用地球磁场信息来实现导航的技术。在无人机领域,磁航技术主要用于辅助惯性导航系统(INS)进行航向角的测量与校正,提高无人机的飞行稳定性和准确性。其技术原理是&#x…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
