OpenGL入门第六步:材质
目录
结果显示
材质介绍
函数解析
具体代码
结果显示

材质介绍
当描述一个表面时,我们可以分别为三个光照分量定义一个材质颜色(Material Color):环境光照(Ambient Lighting)、漫反射光照(Diffuse Lighting)和镜面光照(Specular Lighting)。通过为每个分量指定一个颜色,我们就能够对表面的颜色输出有细粒度的控制了。现在,我们再添加一个反光度(Shininess)分量,结合上述的三个颜色,我们就有了全部所需的材质属性了。
为风氏光照模型的每个分量都定义一个颜色向量。ambient材质向量定义了在环境光照下这个表面反射的是什么颜色,通常与表面的颜色相同。diffuse材质向量定义了在漫反射光照下表面的颜色。漫反射颜色(和环境光照一样)也被设置为我们期望的物体颜色。specular材质向量设置的是表面上镜面高光的颜色(或者甚至可能反映一个特定表面的颜色)。最后,shininess影响镜面高光的散射/半径。有这4个元素定义一个物体的材质,我们能够模拟很多现实世界中的材质。devernay.free.fr中的一个表格展示了一系列材质属性,它们模拟了现实世界中的真实材质。下图展示了几组现实世界的材质参数值对我们的立方体的影响:

可以看到,通过正确地指定一个物体的材质属性,我们对这个物体的感知也就不同了。效果非常明显,但是要想获得更真实的效果,我们需要以更复杂的形状替换这个立方体。
函数解析
timerEvent(QTimerEvent *event)函数:

initializeGL()函数:绘制光源
顶点着色器

片段着色器

环境光通常被认为是均匀地照亮场景的,所以直接用光源的环境光和材质的环境光相乘来简单表示。
漫反射光的强度取决于光线与表面法向量的夹角。通过归一化法向量和光线方向向量,然后计算它们的点积,就能得到光线与表面的夹角余弦值。夹角越小,漫反射光越强,所以用这个点积值来控制漫反射光的强度。
镜面反射光主要是模拟物体表面的高光效果。通过计算反射方向向量和观察方向向量的点积,并对结果进行幂运算,来模拟高光的集中和锐利程度。材质的 shininess 值越大,高光就越集中和锐利。
光源的绘制和前一次(基础光照)没有区别。


paintGL()函数:传参进行绘制

具体代码
.h
#ifndef OPENGLWIDGET_H
#define OPENGLWIDGET_H#include <QOpenGLWidget>
#include <相关文章:

OpenGL入门第六步:材质
目录 结果显示 材质介绍 函数解析 具体代码 结果显示 材质介绍 当描述一个表面时,我们可以分别为三个光照分量定义一个材质颜色(Material Color):环境光照(Ambient Lighting)、漫反射光照(Diffuse Lighting)和镜面光照(Specular Lighting)。通过为每个分量指定一个颜色,…...

新版SpringSecurity5.x使用与配置
目录 一、了解SpringSecurity 1.1 什么是Spring Security? 1.2 Spring Security功能 1.3 Spring Security原理 1.4 RABC (Role-Based Access Control) 二、SpringSecurity简单案例 2.1 引入SpringSecurity依赖 2.2 创建一个简单的Controller 三、SpringSecu…...

JavaScript实战 - JavaScript 中实现线程锁
作者:逍遥Sean 简介:一个主修Java的Web网站\游戏服务器后端开发者 主页:https://blog.csdn.net/Ureliable 觉得博主文章不错的话,可以三连支持一下~ 如有需要我的支持,请私信或评论留言! 前言: …...

基于PaddleClas的人物年龄分类项目
目录 一、任务概述 二、算法研发 2.1 下载数据集 2.2 数据集预处理 2.3 安装PaddleClas套件 2.4 算法训练 2.5 静态图导出 2.6 静态图推理 三、小结 一、任务概述 最近遇到个需求,需要将图像中的人物区分为成人和小孩,这是一个典型的二分类问题…...

20240725java的Controller、DAO、DO、Mapper、Service层、反射、AOP注解等内容的学习
在Java开发中,controller、dao、do、mapper等概念通常与MVC(Model-View-Controller)架构和分层设计相关。这些概念各自承担着不同的职责,共同协作以构建和运行一个应用程序。以下是这些概念的解释:…...

dynslam的安装
1. 安装opencv 2.4.9 下载opencv2.4.9 apt-get install build-essential apt-get install libgtk2.0-dev libavcodec-dev libavformat-dev libtiff4-dev libswscale-dev libjasper-dev apt-get install cmake apt-get install pkg-config 进入安装包文件: m…...

stats 监控 macOS 系统
Stats 监控 macOS 系统 CPU 利用率GPU 利用率内存使用情况磁盘利用率网络使用情况电池电量 brew install stats参考 stats github...

后端面试题日常练-day05 【Java基础】
题目 希望这些选择题能够帮助您进行后端面试的准备,答案在文末 在Java中,以下哪个关键字用于表示方法重写(Override)? a) override b) overrule c) overwrite d) supercede Java中的HashMap和Hashtable有什么区别&am…...

mac|安装PostgreSQL
1、官网下载:EDB: Open-Source, Enterprise Postgres Database Management 选择需要的版本: 双击得到的.dmg文件 双击,弹窗选择打开,一路next,然后输入你要设置的密码,默认账号名字为:postgres…...

内网对抗-隧道技术篇防火墙组策略FRPNPSChiselSocks代理端口映射C2上线
知识点: 1、隧道技术篇-传输层-工具项目-Frp&Nps&Chisel 2、隧道技术篇-传输层-端口转发&Socks建立&C2上线Frp Frp是专注于内网穿透的高性能的反向代理应用,支持TCP、UDP、HTTP、HTTPS等多种协议。可以将内网服务以安全、便捷的方式通过…...
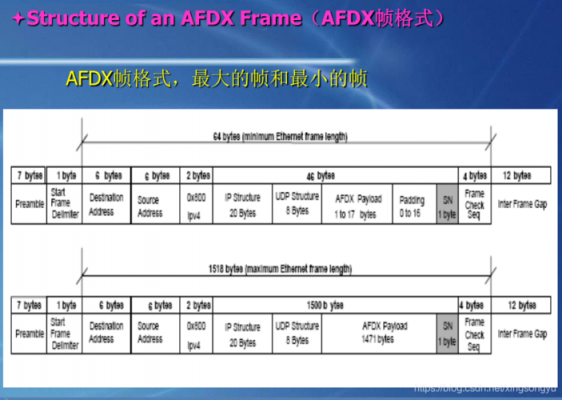
arinc664总线协议
AFDX总线协议简介 (1)AFDX的传输速率高:带宽100MHZ,远远高于其他的类型的航空总线。(2)AFDX网络的鲁棒性高:AFDX的双冗余备份网络可以在某一个网络出现故障时,仍能正常通讯。 其中…...

UNIX 域协议
1. UNIX域协议 利用socket编程接口实现本地进程间通信 UNIX域协议套接字:可以使用TCP,也可以使用UDP SOCK_STREAM -----> TCP 面向字节流 SOCK_DGRAM -----> UDP 面向数据报 UNIX域协议并不是一个实际的协议族,而是在单个主机上执…...

昇思25天学习打卡营第17天|LLM-基于MindSpore的GPT2文本摘要
打卡 目录 打卡 环境准备 准备阶段 数据加载与预处理 BertTokenizer 部分输出 模型构建 gpt2模型结构输出 训练流程 部分输出 部分输出2(减少训练数据) 推理流程 环境准备 pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspo…...

Clion开发STM32——移植FreeModbus
STM32型号 :STM32H743VIT6 FreeModbus版本 :1.6 使用工具:stm32cubeMX,Clion 使用STM32作从机,模式:RTU 网上用keil的比较多,用Clion的比较少,如果你也用Clion,那么希望…...

c++栈笔记
一种常见的数据结构,遵循后进先出,先进后出的原则。地址不连续,栈顶(top) 1.常见函数 stack<int> s;定义一个参数类型为int 的栈 名为ss.push()向栈中插入元素s.emplace()压栈,无返回值s.pop()删除…...

Oracle配置TCPS加密协议测试
文章目录 一、环境信息二、配置过程1.创建证书2.监听配置2.1.配置sqlnet.ora2.2.配置listener.ora文件2.3.配置tnsnames.ora文件2.4.重载监听 3.数据库本地测试3.1. tcps登录测试3.2.日志监控 一、环境信息 操作系统:Linux 版本信息:Oracle 19c 参考文档…...

Jetpack Compose 通过 OkHttp 发送 HTTP 请求的示例
下面是一个使用 Kotlin 和 Jetpack Compose 来演示通过 OkHttp 发送 HTTP 请求的示例。这个示例包括在 Jetpack Compose 中发送一个 GET 请求和一个 POST 请求,并显示结果。 添加okhttp依赖 首先,在你的 build.gradle.kts 文件中添加必要的依赖…...

Pytorch使用教学3-特殊张量的创建与类型转化
1 特殊张量的创建 与numpy类似,PyTorch中的张量也有很多特殊创建的形式。 zeros:全0张量 # 形状为2行3列 torch.zeros([2, 3]) # tensor([[0., 0., 0.], # [0., 0., 0.]])ones:全1张量 # 形状为2行3列 torch.ones([2, 3]) # tensor([[1., 1., 1.], # …...
【日记】办个护照不至于有这种刑事罪犯一样的待遇吧……(737 字)
正文 暴晒,中午出去骑共享单车,座垫都不敢坐。 至于为什么,中午觉都不睡跑出去,是因为今天他们办承兑汇票的业务,搞了一天,中午不休息,说可能还会用到我的指纹,让我 on call。我心想…...

【矩阵微分】在不涉及张量的前提下计算矩阵对向量的导数并写出二阶泰勒展开
本篇内容摘自CMU 16-745最优控制的第10讲 “Nonlinear Trajectory Optimization”。 如何在不涉及张量运算的前提下,计算矩阵对向量的导数并写出二阶泰勒展开 在多维微积分中,计算矩阵对向量的导数和二阶泰勒展开是一项重要的任务。本文将介绍如何在不涉…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
