飞牛爬虫FlyBullSpider 一款简单方便强大的爬虫，限时免费 特别适合小白！用它爬下Boss的2024年7月底Java岗位，分析一下程序员就业市场行情
一、下载安装FlyBullSpider
暂时支持Window,现在只在Win11上做过测试
1 百度
点击百度网盘 下载
链接：https://pan.baidu.com/s/1gSLKYuezaZgd8iqrXhk8Kg
提取码：Fly6
2 csdn
https://download.csdn.net/download/fencer911/89584687
二、体验初探：获取Boss Java岗位数据
飞牛爬虫 设计与运行在一个界面上，在动作编辑界面 还可以提前执行当前的动作。
基本上一行代码不写，一点配置也不改动的情况下，也能爬到数据。
但是，Boss的第一页与以后的页结构不一样，所以同一信息配置了两次，基本就只需要点点就行了。
在动作编辑界面 还可以提前执行当前的动作 . 自定义JS暂未实现，待更新。向下滚动时，值所对应框为向下的滚动的长度。
点击"运行" ，按钮变为运行中 ，执行完了 变回 “运行”
看下结果 。10页的数据300多条。Boss的同一url的数据，每次执行都不一样。点击 “导出” 可导出Excel
任务管理界面 新建任务 编辑 都可进入任务界面，点保存才会保存为json文件
任务文件 task.json 红圈圈的才是关键字段 简单吧！
三、上传excel 分析下数据
数据有重复的，手动在boss点，也会有重复的数据!
保险可以不搞循环(搞循环，也可以不设置"循环结束")，多次运行的数据可以累积在一起。
专科的不好混呀
相关文章：
飞牛爬虫FlyBullSpider 一款简单方便强大的爬虫，限时免费 特别适合小白！用它爬下Boss的2024年7月底Java岗位，分析一下程序员就业市场行情
一、下载安装FlyBullSpider 暂时支持Window,现在只在Win11上做过测试 1 百度 点击百度网盘 下载 链接：https://pan.baidu.com/s/1gSLKYuezaZgd8iqrXhk8Kg 提取码：Fly6 2 csdn https://download.csdn.net/download/fencer911/89584687 二、体验初…...
EXCEL 排名(RANK,COUNTIFS)
1.单列排序 需求描述：如有下面表格，需要按笔试成绩整体排名。 解决步骤： 我们使用RANK函数即可实现单列整体排名。 Number 选择第一列。 Ref 选择这一整列（CtrlShift向下箭头、再按F4）。 "确定"即可计算…...
【踩坑系列-JS】iframe中的url参数获取
Author：赵志乾 Date：2024-07-24 Declaration：All Right Reserved！！！ 1. 问题描述 系统A的页面中以iframe的方式嵌入了系统B的页面，并需要将A页面url中的参数传递给B页面。 最初的实现方式是&am…...
测试工作中常听到的名词解释 : )
背景 很多名称其实看字面意思都挺抽象的，有时看群里的测试大佬在不停蹦这类术语，感觉很高大上，但其实很多你应该是知道的，只不过没想到别人是这样叫它的。又或者你的主编程语言不是 Java，所以看不懂他们在讲啥&#x…...
Linux内网离线用rsync和inotify-tools实现文件夹文件单向同步和双向同步
lsyncd实现方式可参考：https://www.jianshu.com/p/c075ccf89516 安装文件下载：相关文件下载 rsync默认都有，所以没有提供。 服务端和客户端均操作 服务端：双向同步其实都是服务端，只是单向同步时稍有区别 客户端&am…...
Spring Security学习笔记（二）Spring Security认证和鉴权
前言：本系列博客基于Spring Boot 2.6.x依赖的Spring Security5.6.x版本 上一篇博客介绍了Spring Security的整体架构，本篇博客要讲的是Spring Security的认证和鉴权两个重要的机制。 UsernamePasswordAuthenticationFilter和BasicAuthenticationFilter是…...
产品经理NPDP好考吗？
NPDP是新产品开发专业人员的资格认证，对于希望在产品管理领域取得认可的专业人士来说，NPDP认证是一项重要的资格。 那么，产品经理考取NPDP资格认证究竟难不难呢？ 首先，NPDP考试的难易程度取决于考生的背景和准备情况…...
【C++】：红黑树的应用 --- 封装map和set
点击跳转至文章：【C】：红黑树深度剖析 — 手撕红黑树！ 目录 前言一，红黑树的改造1. 红黑树的主体框架2. 对红黑树节点结构的改造3. 红黑树的迭代器3.1 迭代器类3.2 Begin() 和 End() 四，红黑树相关接口的改造4.1 Find…...
unity美术资源优化（资源冗余，主界面图集过多）
图片资源冗余： UPR unity的性能优化工具检查资源 1.检查纹理读/写标记 开启纹理资源的读/写标志会导致双倍的内存占用 检查Inspector -> Advanced -> Read/Write Enabled选项 2.检查纹理资源alpha通道 如果纹理的alpha通道全部为0，或者全部为2…...
【git】github中的Pull Request是什么
在 Git 中，"pull request"（简称 PR）是一种在分布式版本控制系统中使用的功能，特别是在使用 GitHub、GitLab、Bitbucket 等基于 Git 的代码托管平台时。Pull Request 允许开发者请求将他们的代码更改合并到另一个分支&am…...
gitlab查询分支API显示不全，只有20个问题
背景 gitlab查询分支API需要查询所有分支，且分支数量大于20，但目前调用接口返回的branch最多就显示了20个 解决方案 根据GitLab的文档，查询分支API默认最多返回20个分支。如果要一次性显示80个分支，可以使用分页参数来获取所有…...
vue3+vite 实现动态引入某个文件夹下的组件 - glob-import的使用
<template><div class"user-content"><HeaderTitle title"用户详情"></HeaderTitle><div class"main-content"><div><UserForm /></div><div><TableList></TableList></d…...
hhhhh
x torch.tensor([1.0,0.],[-1.,1.],requires_gradTrue) z x.pow(2).sum() z.backward() x.grad在这段代码中，我们利用 PyTorch 进行自动求梯度，下面详细解释代码的每一个部分及其在反向传播中的作用。同时，我们也将介绍函数对象和叶子节点的…...
扫雷小游戏纯后端版
package com.wind;import java.util.Random; import java.util.Scanner;public class ResultLei {static Random random new Random();public static void main(String[] args) {boolean end true;while (end) {System.out.println("请输入你选择的难度对应的数字&#…...
RuoYi-Vue-Plus（动态添加移除数据源）
一、添加数据 private final DynamicRoutingDataSource dynamicRoutingDataSource;private final DefaultDataSourceCreator dataSourceCreator;//添加一个dynamic的数据源@GetMapping("createDynamic")public void createDynamic() {DataSourceProperty property =…...
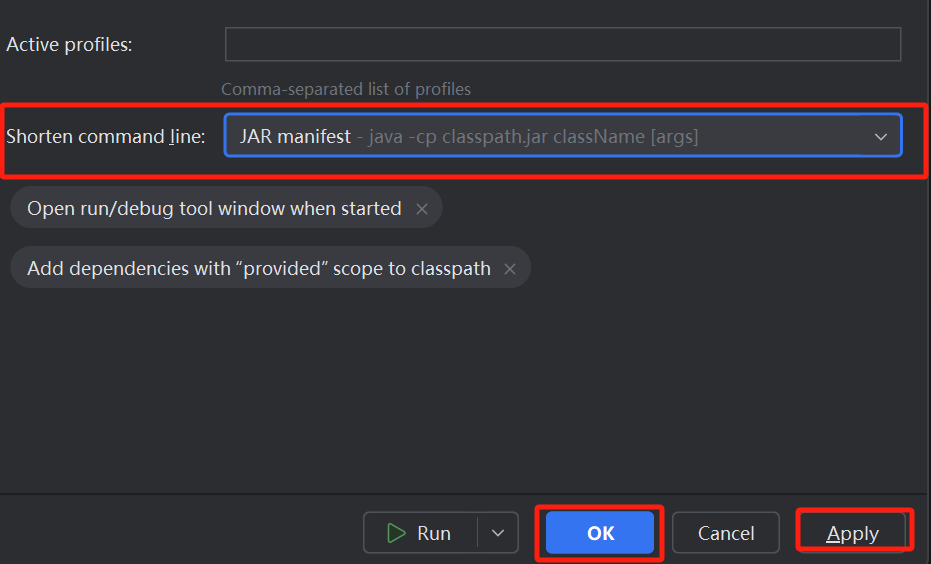
idea启动项目报：the command line via JAR manifest or via a classpath file and rerun.
解决方案 1.打开Edit Configurations，进去编辑，如下： 笔记配置 2.选择Modfiy options,点击Shorten command line 3.在新增的Shorten command line选项中选择JAR manifest或classpath file 4.点击保存后即可...
vue3 + ts中有哪些类型是由vue3提供的?
在 Vue 3 中结合 TypeScript 使用时，Vue 提供了一系列的类型帮助函数和接口，这些类型用于增强 TypeScript 的集成和提供类型安全。以下是一些由 Vue 3 提供的常用 TypeScript 类型： RefType: 用于标注一个 ref 返回的响应式引用类型。Reacti…...
【Linux】远程连接Linux虚拟机（MobaXterm）
【Linux】远程连接Linux虚拟机（MobaXterm） 零、原因 有时候我们在虚拟机中操作Linux不太方便，比如不能复制粘贴，不能传文件等等，我们在主机上使用远程连接软件远程连接Linux虚拟机后可以解决上面的问题。 壹、软件下…...
LeetCode Hot100 生成特殊数字的最少操作
给你一个下标从 0 开始的字符串 num ，表示一个非负整数。 在一次操作中，您可以选择 num 的任意一位数字并将其删除。请注意，如果你删除 num 中的所有数字，则 num 变为 0。 返回最少需要多少次操作可以使 num 变成特殊数字。 如…...
Spring MVC 应用分层
1. 类名使⽤⼤驼峰⻛格，但以下情形例外：DO/BO/DTO/VO/AO 2. ⽅法名、参数名、成员变量、局部变量统⼀使⽤⼩驼峰⻛格 3. 包名统⼀使⽤⼩写，点分隔符之间有且仅有⼀个⾃然语义的英语单词. 常⻅命名命名⻛格介绍 ⼤驼峰: 所有单词⾸字⺟…...
突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合
强化学习（Reinforcement Learning, RL）是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程，然后使用强化学习的Actor-Critic机制（中文译作“知行互动”机制），逐步迭代求解…...
Appium+python自动化（十六）- ADB命令
简介 Android 调试桥(adb)是多种用途的工具，该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具，其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利，如安装和调试…...
定时器任务——若依源码分析
分析util包下面的工具类schedule utils： ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类，封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz，先构建任务的 JobD…...
新能源汽车智慧充电桩管理方案：新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及，充电桩作为核心配套设施，其安全性与可靠性备受关注。然而，在高温、高负荷运行环境下，充电桩的散热问题与消防安全隐患日益凸显，成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性：使神经网络可学习复杂模式控制输出范围：如Sigmoid将输出限制在(0,1)梯度传递：影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程：首先由HR先筛选一部分简历后，在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如：Boss直聘（招聘方平台） 直接按照条件进行筛选 例如：…...
C++：多态机制详解
目录 一. 多态的概念 1.静态多态（编译时多态） 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1）.协变 2）.析构函数的重写 5.override 和 final关键字 1&#…...
【Linux】Linux 系统默认的目录及作用说明
博主介绍：✌全网粉丝23W，CSDN博客专家、Java领域优质创作者，掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围：SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值，最大值左侧的数值严格单调递增，最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值，最小值左侧的数值严格单调递减，最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...