LeetCode-day27-3106. 满足距离约束且字典序最小的字符串
LeetCode-day27-3106. 满足距离约束且字典序最小的字符串
- 题目描述
- 示例
- 示例1:
- 示例2:
- 示例3:
- 思路
- 代码
题目描述
给你一个字符串 s 和一个整数 k 。
定义函数 distance(s1, s2) ,用于衡量两个长度为 n 的字符串 s1 和 s2 之间的距离,即:
- 字符 ‘a’ 到 ‘z’ 按 循环 顺序排列,对于区间 [0, n - 1] 中的 i ,计算所有「 s1[i] 和 s2[i] 之间 最小距离」的 和 。
例如,distance(“ab”, “cd”) == 4 ,且 distance(“a”, “z”) ==1 。
你可以对字符串 s 执行 任意次 操作。在每次操作中,可以将 s 中的一个字母 改变 为 任意 其他小写英文字母。
返回一个字符串,表示在执行一些操作后你可以得到的 字典序最小 的字符串 t ,且满足 distance(s, t) <= k 。
示例
示例1:
输入:s = “zbbz”, k = 3
输出:“aaaz”
解释:在这个例子中,可以执行以下操作:
将 s[0] 改为 ‘a’ ,s 变为 “abbz” 。
将 s[1] 改为 ‘a’ ,s 变为 “aabz” 。
将 s[2] 改为 ‘a’ ,s 变为 “aaaz” 。
“zbbz” 和 “aaaz” 之间的距离等于 k = 3 。
可以证明 “aaaz” 是在任意次操作后能够得到的字典序最小的字符串。
因此,答案是 “aaaz” 。
示例2:
输入:s = “xaxcd”, k = 4
输出:“aawcd”
解释:在这个例子中,可以执行以下操作:
将 s[0] 改为 ‘a’ ,s 变为 “aaxcd” 。
将 s[2] 改为 ‘w’ ,s 变为 “aawcd” 。
“xaxcd” 和 “aawcd” 之间的距离等于 k = 4 。
可以证明 “aawcd” 是在任意次操作后能够得到的字典序最小的字符串。
因此,答案是 “aawcd” 。
示例3:
输入:s = “lol”, k = 0
输出:“lol”
解释:在这个例子中,k = 0,更改任何字符都会使得距离大于 0 。
因此,答案是 “lol” 。
思路
贪心策略。
- 从左到右遍历 s。
- 如果把 s[i] 变成 a 的操作次数 dis≤k,那么就把 s[i] 变成 a,同时 k 减少 dis。
- 否则无法变成 a,直接把 s[i] 减少 k,退出循环。
代码
class Solution:def getSmallestString(self, s: str, k: int) -> str:s = list(s)p = []for i in range(len(s)):p.append(ord(s[i]))for i,x in enumerate(p):dis = min(x- ord('a'),ord('z') - x + 1)if dis > k:s[i] = chr(x-k)breaks[i] = 'a'k -= disreturn ''.join(s)
相关文章:

LeetCode-day27-3106. 满足距离约束且字典序最小的字符串
LeetCode-day27-3106. 满足距离约束且字典序最小的字符串 题目描述示例示例1:示例2:示例3: 思路代码 题目描述 给你一个字符串 s 和一个整数 k 。 定义函数 distance(s1, s2) ,用于衡量两个长度为 n 的字符串 s1 和 s2 之间的距…...

C++中的static_cast函数
static_cast 是 C 中的一个类型转换操作符,用于在编译时进行类型转换。它主要用于基本数据类型之间的转换,以及类的指针或引用之间的向上转换(将派生类指针或引用转换为基类指针或引用)和某些情况下的向下转换(将基类指…...

从零开始学习网络安全渗透测试之基础入门篇——(二)Web架构前后端分离站Docker容器站OSS存储负载均衡CDN加速反向代理WAF防护
Web架构 Web架构是指构建和管理Web应用程序的方法和模式。随着技术的发展,Web架构也在不断演进。当前,最常用的Web架构包括以下几种: 单页面应用(SPA): 特点:所有用户界面逻辑和数据处理都包含…...

2679. 矩阵中的和
两种方法: 第一种:先对二维列表的每一列进行排序,然后对每一列的数据进行逐个比较,找出最大值。 class Solution:def matrixSum(self, nums: list[list[int]]) -> int:result0mlen(nums)nlen(nums[0])for i in range(m):nums…...

Unity Playables:下一代动画与音频序列
Unity的Playables API是一种灵活的系统,用于创建和控制动画、音频以及其他形式的连续媒体序列。它为开发者提供了一种全新的方法来处理游戏中的时间序列,包括动画、音频、特效等。本文将探讨Playables的基本概念、如何使用Playables API实现动画…...

matlab仿真 模拟调制(下)
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第五章内容,有兴趣的读者请阅读原书) clear all ts0.001; t0:ts:10-ts; fs1/ts; dffs/length(t); msgrandi([-3 3],100,1); msg1msg*ones(1,fs/10); msg2reshape(ms…...

RabbitMQ是什么?
RabbitMQ是一个开源的消息代理软件(Message Broker),它实现了高级消息队列协议(AMQP,Advanced Message Queuing Protocol),并支持多种消息传递协议。它最初由英国的Rabbit Technologies开发&…...

追问试面试系列:分布式id
hi 大家好,欢迎来到追问试面试系列:分布式id 面试中可能面试官不会直接问你分布式id问题,基本上都是因为你在某些面试题回答中提到了,所以就开始追问分布式id相关问题。 先看面试题 ● 面试官:什么是分布式id? ● 面试官:举个例子说说 ● 面试官:什么叫分库分表? ●…...

护网紧急情况应对指南:Linux 应急响应手册
继上一篇:护网紧急情况应对指南:Windows版v1.2全新升级版 之后 收到小伙伴后台要Linux应急手册,今天给大家安排上。 《Linux应急手册》是一本为Linux系统管理员和运维工程师量身打造的实用指南,旨在帮助他们快速应对各种突发状况…...

WEB攻防-通用漏洞-SQL 读写注入-MYSQLMSSQLPostgreSQL
什么是高权限注入 高权限注入指的是攻击者通过SQL注入漏洞,利用具有高级权限的数据库账户(如MYSQL的root用户、MSSQL的sa用户、PostgreSQL的dba用户)执行恶意SQL语句。这些高级权限账户能够访问和修改数据库中的所有数据,甚至执行…...
【前端学习笔记】CSS基础一
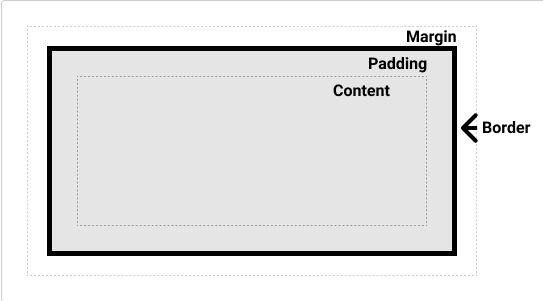
一、什么是CSS 1.CSS 介绍 CSS(Cascading Style Sheets,层叠样式表)是一种用来控制网页布局和设计外观的样式语言。它使得开发者可以分离网页的内容(HTML)和表现形式(样式),提高了…...
)
Github遇到的问题解决方法总结(持续更新...)
1.github每次push都需要输入用户名和token的解决方法 push前,执行下面命令 : git config --global credential.helper store 之后再输入一次用户名和token之后,就不用再输入了。 2.git push时遇到“fatal: unable to access https://githu…...

数字信封+数字签名工具类测试样例(Java实现)
加解密过程 加密: 生成加密方SM2密钥对用于签名使用生成的SM2私钥生成数字签名生成SM4对称密钥对明文进行对称加密使用与解密方提前约定好的SM2公钥对第三步中的SM4对称密钥进行非对称加密把【加密方SM2公钥】、【数字签名】、【SM4对称加密后的密文】和【SM2非对…...

The Schematic workflow failed. See above.
在使用 ng new 新建Angular项目的时候会报一个错误:The Schematic workflow failed. See above. 解决办法: 只需要在后面加上 --skip-install 参数,就不会报错了。 ng new myapp --skip-install...
操作系统面试知识点总结4
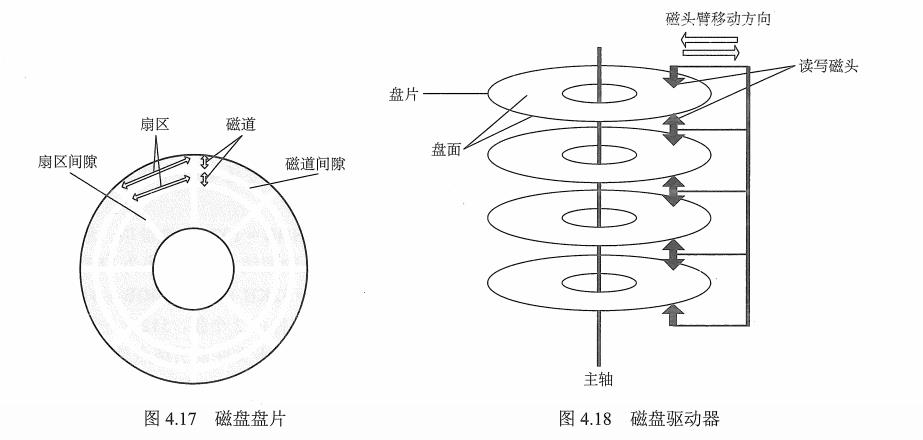
#来自ウルトラマンメビウス(梦比优斯) 1 文件系统基础 1.1 文件的相关概念 文件是以计算机硬盘为载体的存储在计算机上的信息集合,可以是文本文档、图片、程序。 文件的结构:数据项、记录、文件(有结构文件、无结构式…...

Lua实现面向对象以及类的继承
0.简单前言 1、面向对象主要四个特征:封装,继承,多态,抽象 2、Lua是种简单精致小巧的语言,其本质是个表(table),变量和方法皆可看作为该表的元素。 P.S. 该博客和代码为个人编写习…...
机器学习课程学习周报五
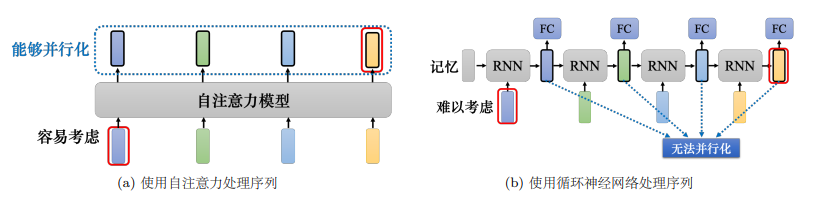
机器学习课程学习周报五 文章目录 机器学习课程学习周报五摘要Abstract一、机器学习部分1.1 向量序列作为模型输入1.1.1 文字的向量表达1.1.2 语音的向量表达 1.2 自注意力机制原理1.2.1 自注意力机制理论1.2.2 矩阵运算自注意力机制 1.3 多头自注意力1.4 位置编码1.5 截断自注…...

vue3.0学习笔记(二)——生命周期与响应式数据(ref,reactive,toRef,toRefs函数)
1. 组合API-setup函数 使用细节: setup 是一个新的组件选项,作为组件中使用组合API的起点。从组件生命周期来看,它的执行在组件实例创建之前vue2.x的beforeCreate执行。这就意味着在setup函数中 this 还不是组件实例,this 此时是…...

C++——QT:保姆级教程,从下载到安装到用QT写出第一个程序
登录官网,在官网选择合适的qt版本进行下载 这里选择5.12.9版本 点击exe文件下载,因为服务器在国外,国内不支持,所以可以从我的网盘下载 链接: https://pan.baidu.com/s/1XMILFS1uHTenH3mH_VlPLw 提取码: 1567 --来自百度网盘超级…...
掌握互联网路由选择协议:从基础入门到实战
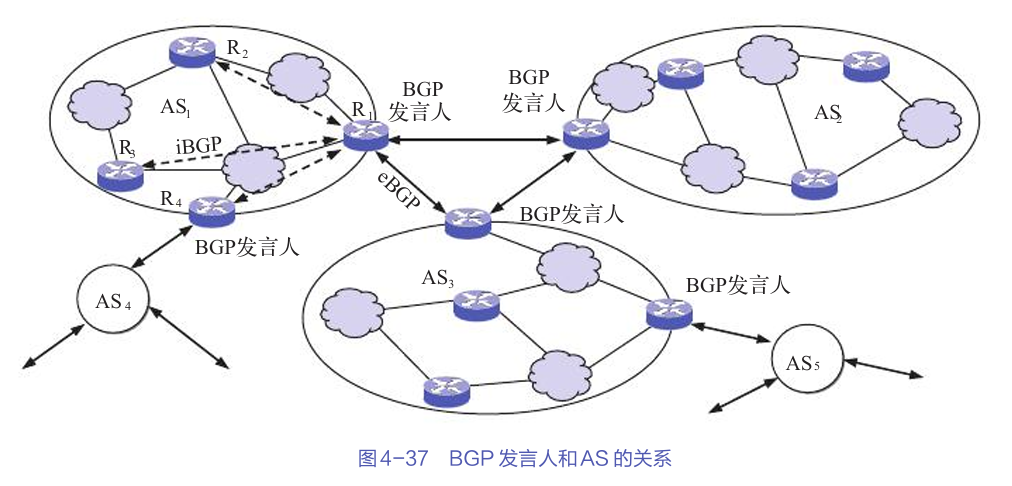
文章目录 路由选择协议的基本概念路由选择算法的分类分层次的路由选择协议路由信息协议(RIP)内部网关协议:OSPF外部网关协议:BGP互联网中的实际应用总结 互联网的路由选择协议是网络通信的核心,它决定了数据包如何在网…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
