西安石油大学C语言期末真题实战

很简单的一道程序阅读题,p=a’默认为a【0】,接下来会进行3次循环 0 1 2 输出结果即可

前3题就是一些基础定义,在此不多赘述
要注意不同的数据类型的字节数不同
a<<2 b>>1(b>>1;就是说b自身右位移一位(参考位运算)
“>>”位移运算,就是把b转换为二进制数,整体向右移一位,高位补零,最低位消失,通常右移一位就等价于b除以2再赋给b)
连接两个字符串用的函数是Strcat


#include <stdio.h>int main() {int a, b, c, d, i, max;c = 0;b = 0;i = 1;while (i <= 10) {scanf("%d", &a);if (a < b)b = a;i++;}printf("最小数是:%d", b);return 0;
}#include<stdio.h>int main(){int a,b,sum=0;for(a=1;a<=1000;a++);{b=a%2;if(b!=0){sum+=a;}print("sum=%d\n",sum);}return 0;}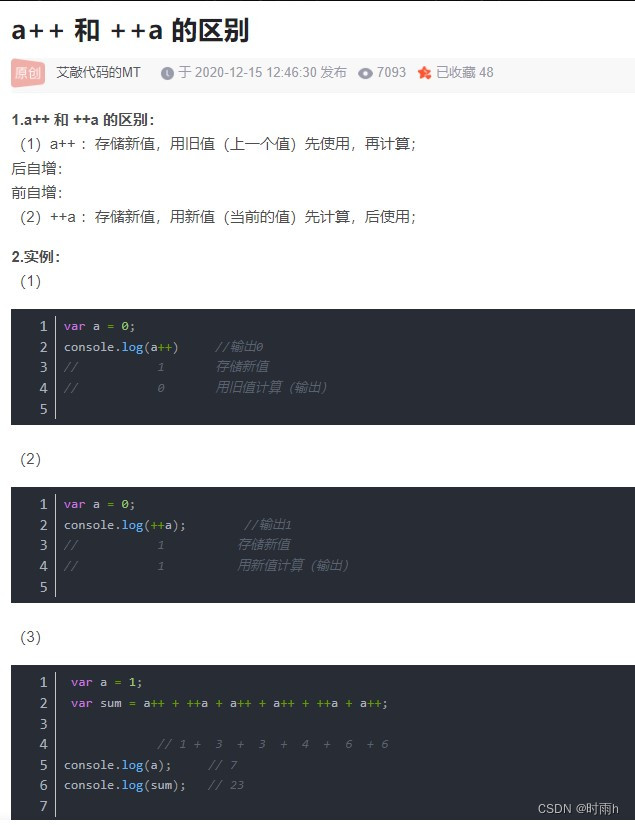
注意++和a谁在前即可


循环3次 和 验证输入的字符是否是密码

运算的优先级不同

++和j的先后

++和j的先后
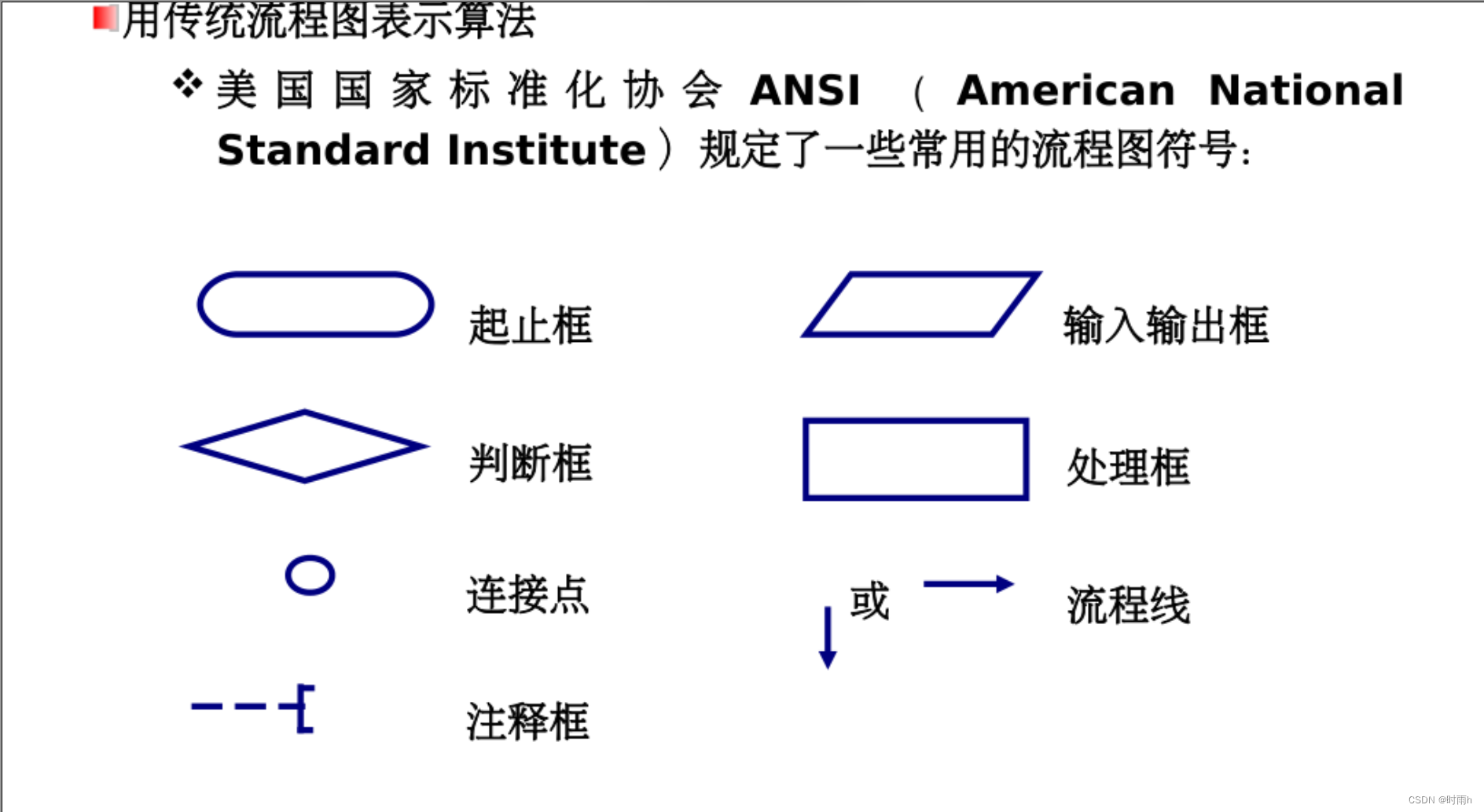
流程表符号



 、
、
在比较大小的同时也要再加上这个数是第几个即可

C语言的编译过程

基本定义 但也要重视!

switch语句即可解决

相关文章:

西安石油大学C语言期末真题实战
很简单的一道程序阅读题,pa’默认为a【0】,接下来会进行3次循环 0 1 2 输出结果即可 前3题就是一些基础定义,在此不多赘述 要注意不同的数据类型的字节数不同 a<<2 b>>1(b>>1;就是说b自身右位移一位(…...

【Shell】Shell变量
Shell变量系统预定义变量自定义变量基本语法定义变量撤销变量命名规则使用变量只读变量删除变量变量类型系统预定义变量 $HOME、$PWD、$SHELL、$SUSER等 实例 yysubuntu:~$ echo $HOME #查看系统变量的值 /home/yys yysubuntu:~$ set #显示当前shell中所有变量自定义变量…...
你是真的“C”——结构体中鲜有人知的“秘密”
你是真的“C”——结构体中的精髓剖析【内存对齐】 【位段】 😎前言🙌结构体内存对齐:😊结构体内存对齐存在的意思是什么?😘内存对齐例子详细剖析:😘结构体中的位段:&…...
)
2023年“网络安全”赛项江苏省淮安市赛题解析(超详细)
2023年中职组江苏省淮安市“网络空间安全”赛项 ①.2023年中职组江苏省淮安市任务书②.2023年中职组江苏省淮安市解析③.需要环境或者不懂的可以私信博主!①.2023年中职组江苏省淮安市任务书 任务一:服务器内部信息获取 任务环境说明: 服务器场景:Server210510(关闭链接…...

【二分查找】
二分查找704. 二分查找35. 搜索插入位置34. 在排序数组中查找元素的第一个和最后一个位置结语704. 二分查找 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在…...
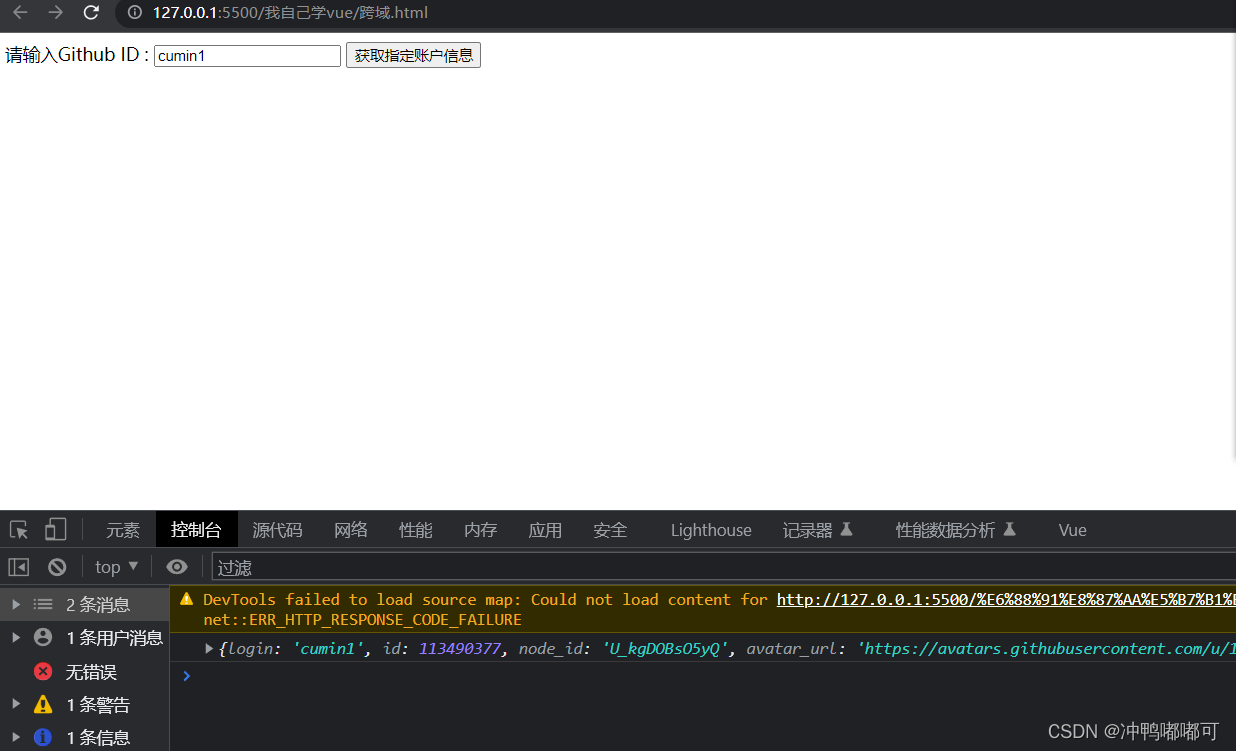
Vue学习 -- 如何用Axios发送请求(get post)Promise对象 跨域请求问题
什么是Axios Vue本身是不支持发送axios请求,需要使用第三方插件,这里推荐使用Axios,Axios是基于promise的HTTP库;它会从浏览器中创建XMLHttpRequset对象。 安装Axios npm install axios -S下载后把axios.js文件复制进项目目录 …...

TVS和稳压管的相同点和不同点
大家好,我是记得诚。 文章目录 介绍相同点不同点介绍 TVS和稳压管都是电路中很常用的电子元器件,都是二极管的一个种类。 TVS二极管全称是Transient voltage suppression diode,也叫瞬态电压抑制二极管。 稳压二极管英文名字Zener diode,又叫齐纳二极管。 关于稳压二极…...

微信小程序项目实例——扫雷
今日推荐💁♂️ 2023许嵩演唱会即将到来🎤🎤🎤大家一起冲冲冲🏃♂️🏃♂️🏃♂️ 🔮🔮🔮🔮🔮往期优质项目实例🔮…...
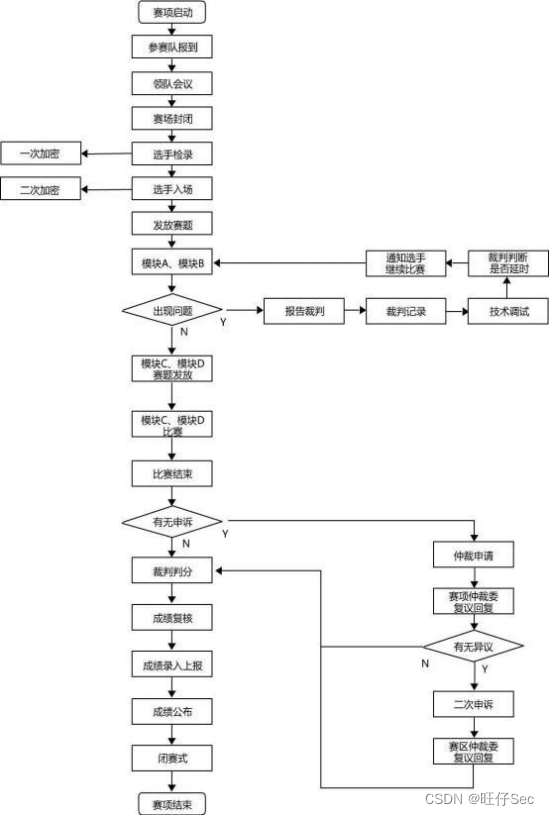
2022-2023年度广东省职业院校学生专业技能大赛 中职组网络安全赛项竞赛规程
2022-2023年度广东省职业院校学生专业技能大赛 中职组网络安全赛项竞赛规程 一、赛项名称 赛项编号:Z27 赛项名称:网络安全赛项组别:中职 赛项归属:信息技术类 二、竞赛目的 为检验中职学校网络信息安全人才培养成效,促…...
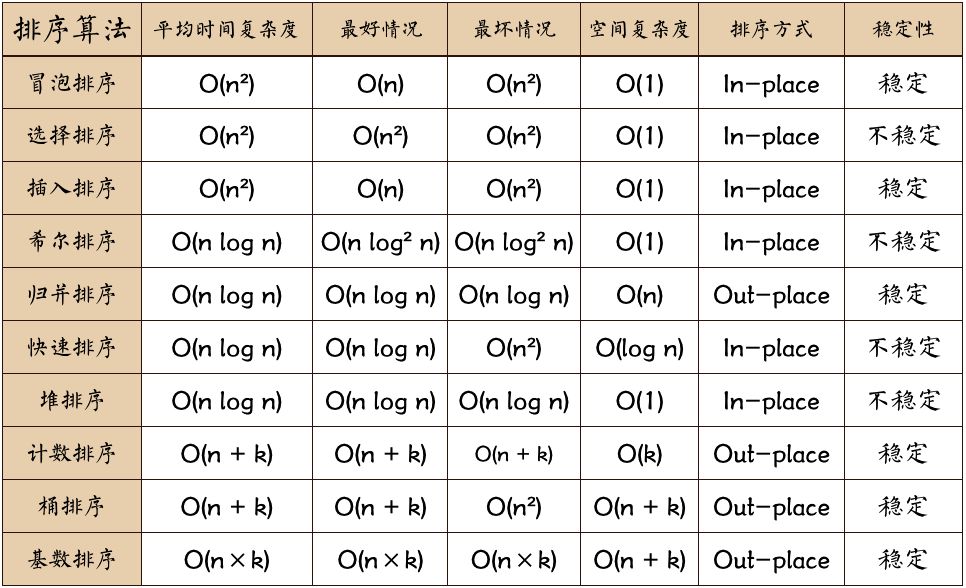
超详细的堆排序,进来看看吧。
1.堆的基本概念1.1什么是堆堆是一种叫做完全二叉树的数据结构,1.2大堆和小堆大堆:每个节点的值都大于或者等于他的左右孩子节点的值小根堆:每个结点的值都小于或等于其左孩子和右孩子结点的值1.3完全二叉树节点之间的关系leftchild parent*2 1rightchild parent*…...
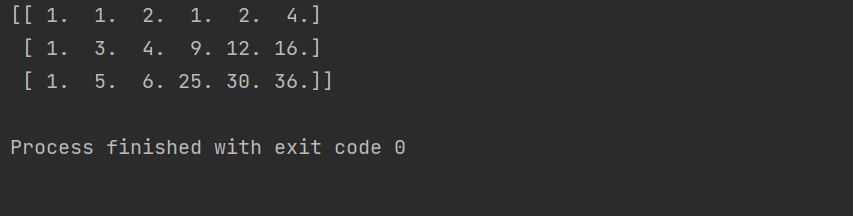
线性回归 特征扩展的原理与python代码的实现
文章目录1 多项式扩展的作用2 多项式扩展的函数2.1 接收参数2.2 多项式扩展示例3 多项式扩展的完整实例1 多项式扩展的作用 在线性回归中,多项式扩展是种比较常见的技术,可以通过增加特征的数量和多项式项的次数来提高模型的拟合能力。 举个例子&#…...

订阅关系一致
订阅关系一致指的是同一个消费者Group ID下所有Consumer实例所订阅的Topic、Tag必须完全一致。如果订阅关系不一致,消息消费的逻辑就会混乱,甚至导致消息丢失。本文提供订阅关系一致的正确示例代码以及订阅关系不一致的可能原因,帮助您顺畅地订阅消息。 背景信息 消息队列Ro…...

测试老鸟都在用的接口抓包常用工具以及接口测试工具都有哪些?
目录 接口 接口测试的重要性 常用抓包工具 常用接口测试工具 接口 接口测试是测试系统组件间接口的一种测试。接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。测试的重点是要检查数据的交换,传递和控制管理过程,以及系统间…...
Delphi 一个函数实现腾讯云最新版(API3.0)短信发送
目录 一、腾讯云短信基本知识 1. 需要在腾讯云后台注册账号 2. 需要在腾讯云中开通短信功能 3. 腾讯云短信版本说明 4. 短信内容的组成 特定规范 二、短信发送函数 三、下载源代码(收费) 一、腾讯云短信基本知识 如今我们随时都收到短信验证码,注册码等等。这是…...

2023年Android现代开发
2023年现代Android开发 下面与大家分享如何构建具有2023年最新趋势的Android应用程序。 Android是什么? Android 是一种基于 Linux 内核并由 Google 开发的开源操作系统。它用于各种设备,包括智能手机、平板电脑、电视和智能手表。 目前,…...

自然语言处理(NLP)在医疗领域的应用
自然语言处理(Natural Language Processing,NLP)是计算机科学领域与人工智能领域中的一个重要方向。它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。在各个领域都有其应用。 其在生物医学领域迅速发展,已经…...

计算机中的浮点数运算
计算机中的浮点数 计算机中以固定长度存储浮点数的方式,造成了浮点数运算过程容易产生上溢和下溢。以float32为例, 其标记位占1bit,指数位占8bit,小数部分占23bit 经典下溢场景 不满足精度导致截断误差 #include <iostream> #include <iomanip> usin…...

看了字节跳动月薪20K+测试岗面试题,让我这个工作3年的测试工程师,冷汗直流....
朋友入职已经两周了,整体工作环境还是非常满意的!所以这次特意抽空给我写出了这份面试题,而我把它分享给伙伴们,面试&入职的经验! 大概是在2月中的时候他告诉我投递了字节跳动并且简历已通过,2月23经过…...
这两天最好的ChatGPT应用;使用Notion AI提升效率的经验(13);AI编程与程序员的生存 | ShowMeAI日报
👀日报合辑 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🤖 硅谷银行风波中,OpenAI 创始人大方帮助硅谷初创公司:钱先拿着用,有了再还 OpenAI 创始人 Sam Altman 的弟弟…...

Linux 内核likely与unlikey
内核源码的时候经常可以看到likely()和unlikely()函数,这两个函数的作用是什么?-- 先得学一学GCC提供的内建函数!! likely和unlikely内核中的定义 # define likely(x) __builtin_expect(!!(x), 1) # define unlikely(x) __built…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...