尺取法
尺取法是一种线性的高效率算法。记 (L, R ) 为一个序列内以L为起点的最短合法区间,
如果R随L的增大而增大的,就可以使用尺取法。具体的做法是不断的枚举 L,同时求出R。
因为 R 随 L增大而增大,所以总时间复杂度为 O(n)
指针i、j的两种方向:
反向扫描:i、j方向相反,i从头到尾,j从尾到头,在中间相会。 “左右指针”
同向扫描:i、j方向相同,都从头到尾,速度不同,例如让j跑在i前面。 “快慢指针”
反向扫描:回文判定
【题目描述】给定一个长度为 n 的字符串 S。请你判断字符串 S是否回文。
【输入描述】输入仅1行包含一个字符串S。1≤|S|≤10**6,保证S只包含大小写、字母。
【输出描述】若字符串S为回文串,则输出Y,否则输出N。
反向扫描的两个指针i、j,指针i从左向右扫描,指针j从右向左扫描,在中间i < j处相遇并停止
s = input()
i = 0
j = len(s) - 1
if i == j:print('Y')
else:while s[i] == s[j]:i += 1j -= 1if j <= i:print('Y')breakelse:print("N"相关文章:

尺取法
尺取法是一种线性的高效率算法。记 (L, R ) 为一个序列内以L为起点的最短合法区间, 如果R随L的增大而增大的,就可以使用尺取法。具体的做法是不断的枚举 L,同时求出R。 因为 R 随 L增大而增大,所以总时间复杂度为 O(n) 指针i、j的两种方向: 反向扫描:i、j方向相反,i从头…...

20.有效的括号
给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都有一个对应的相同类型的左括…...

使用QT C++编写一个带有菜单和工具条的文本编辑器
您好,这是必应。我可以帮您生成一段使用QT C编写一个带有菜单和工具条的文本编辑器的代码,但是请注意,这只是我的创造性的输出,并不代表任何权威或专业的观点。如果您想要了解更多的相关知识,请自行搜索或咨询专家。以…...

文法和语言的基本知识
一、什么形式化的方法用一套带有严格规定的符号体系来描述问题的方法二、什么是非形式化的方法对程序设计语言的描述从语法、语义和语用三个方面因素来考虑所谓语法是对语言结构定义所谓语义是描述了语言的含义所谓语用则是从使用的角度去描述语言三、符号串字母表和符号串字母…...

学习其他人的代码,成为更好的程序员
学习其他人的代码,成为更好的程序员1. 广泛阅读2. 分析代码3. 记笔记4. 实验5. 分享你的发现6. 结论参考如何成为一名更好的Python程序员??? 学习编码是一个持续的过程,需要实践、实验和向他人学习的意愿。提高编码技能的最佳方法之一是学习他人的代…...

新星计划-JAVA学习路线及书籍推荐
CSDN的各位友友们你们好,今天千泽为大家带来的是JAVA学习路线及其经典书籍推荐,接下来让我们一起了解一下JAVA的学习路线吧!如果对您有帮助的话希望能够得到您的支持和关注,我会持续更新的! 目录 1.JAVASE及其书籍推荐 2.初级数据结构与算法及其书籍推荐 3.MySQL及其书籍推荐…...

【大数据】Hive系列之- Hive-DML 数据操作
Hive系列-DML 数据操作数据导入向表中装载数据(Load)语法操作用例通过查询语句向表中插入数据(Insert)创建一张表插入数据基本模式插入(根据单张表查询结果)查询语句中创建表并加载数据(As Sele…...

day2 —— 判断字符串中的字符是否唯一
目录 前言 问题描述 代码解释 前言 若是想要了解基本语法的话,请到(7条消息) C语言从练气期到渡劫期_要一杯卡布奇诺的博客-CSDN博客查看相应的语法细节 强烈安利这篇文章 —— (4条消息) 筑基五层 —— 位运算看这篇就行了_要一杯卡布奇诺的博客-CSDN博客 问题…...

176万,GPT-4发布了,如何查看OpenAI的下载量?
大家好,这里是程序员晚枫。 昨天新一代GPT4发布了,今年GPT不断给大家带来惊喜。 在OpenAI的官网,也公开了GPT的Python调用第三方库:openai。 今天我们就来看看,这个Python智能接口~ 1、代码说明 开发过Python项目…...

蓝蓝算法题(一)
讲在前面:1.本人正在逐步学习C,代码中难免有C和C(向下兼容)混用情况。2.算法题目来自蓝蓝知识星球,没有对应的判决系统,运行到判决系统可以会有部分案例不能通过。 求素数 暴力求解(1 - n试探…...
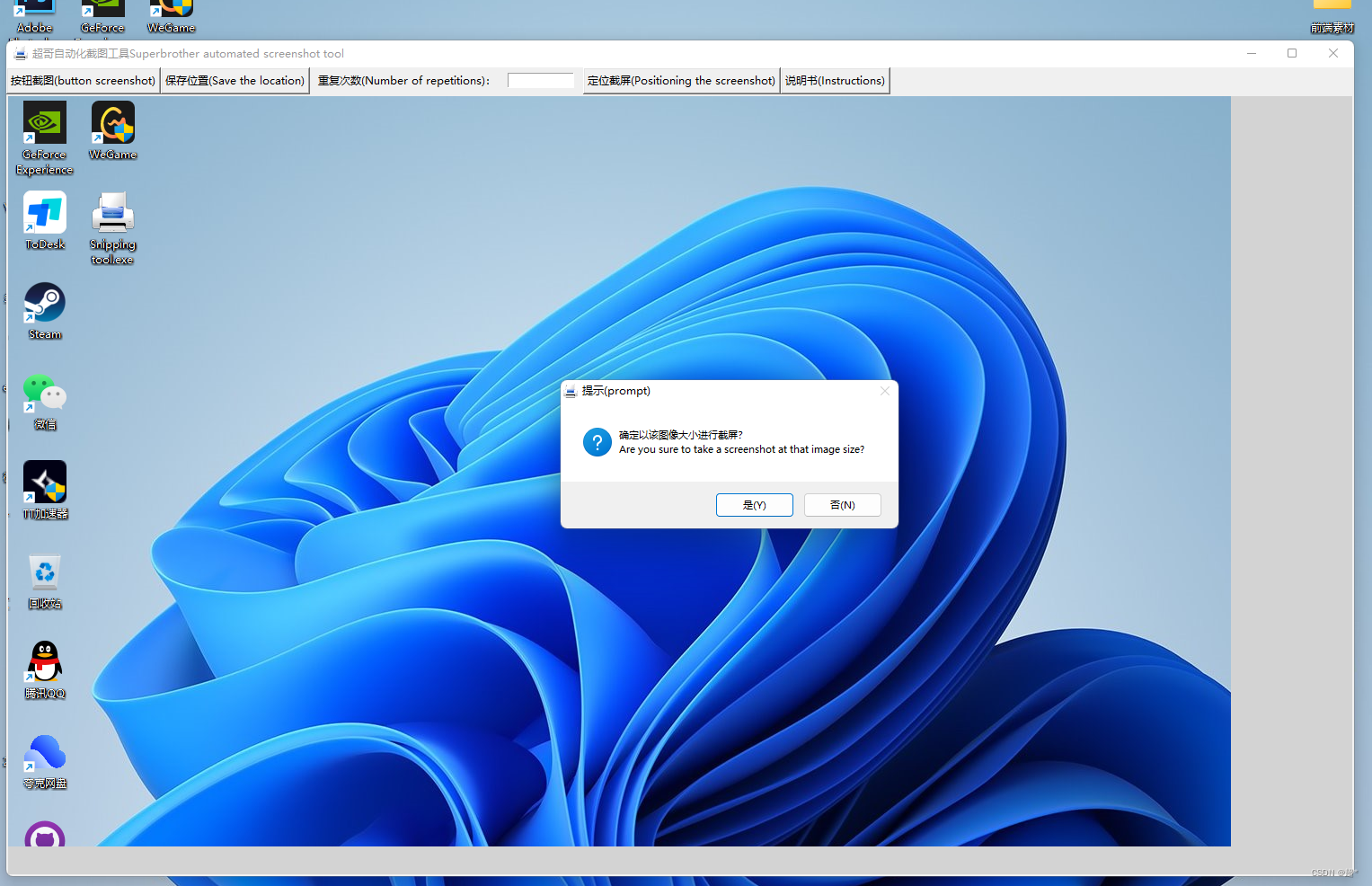
Python截图自动化工具
1、展示部分源码(写的比较乱,哈哈) 2、功能展示 1)首页 2)按钮截图(用于自动翻页) 3)保存位置按钮(选择图片保存的位置) 4)重复次数,就是要截取多少次 5)定位截屏(截取的内容&#x…...

网络作业2【计算机网络】
网络作业2【计算机网络】前言推荐网络作业2一. 单选题(共3题,19.8分)二. 多选题(共1题,6.6分)三. 填空题(共8题,52.8分)四. 判断题(共3题,20.8分&…...

如何给网页加速,如何加速网页速度?
如何加速网页速度?提高移动网页加载的速度,可以从服务器的优化、网页的容量、请求响应等方面入手,这些方面优化后必然可以提高加载速度。1、服务器硬件软件配置要好,网络、读写响应等要做好优化。2、可以开启gzip压缩技术…...
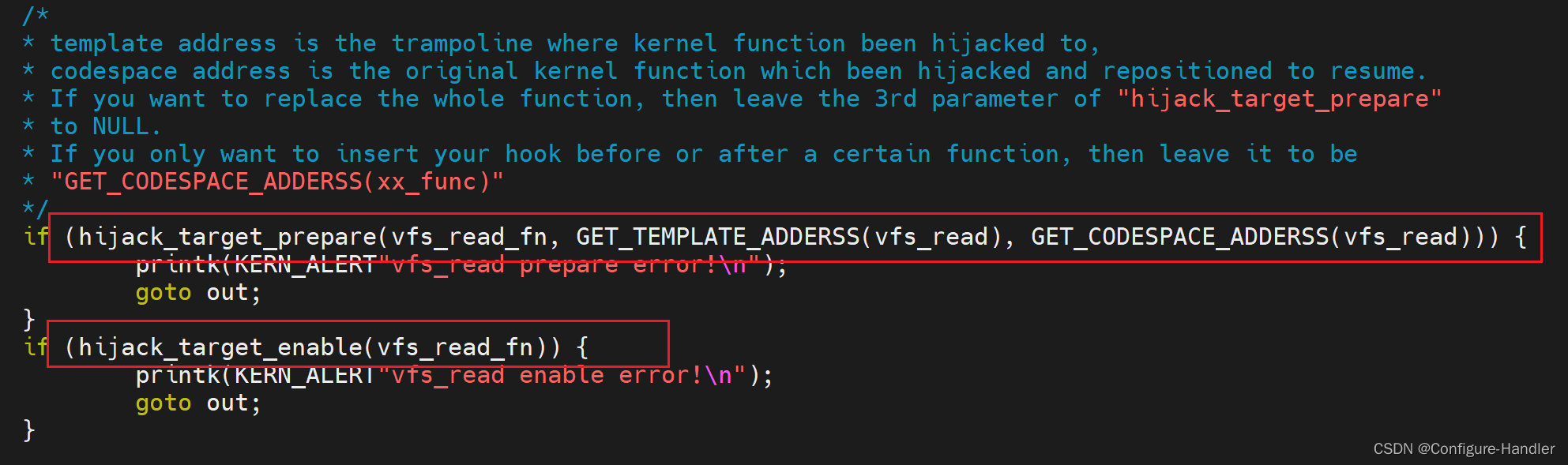
linux kernel 5.0 inline hook框架
github:https://github.com/WeiJiLab/kernel-hook-framework 一、项目介绍 Usually we want to hack a kernel function, to insert customized code before or after a certain kernel function been called, or to totally replace a function with new one. How can we…...

【Java版oj】day12二进制插入、查找组成一个偶数最接近的两个素数
目录 一、二进制插入 (1)原题再现 (2)问题分析 (3)完整代码 二、查找组成一个偶数最接近的两个素数 (1)原题再现 (2)问题分析 (3࿰…...
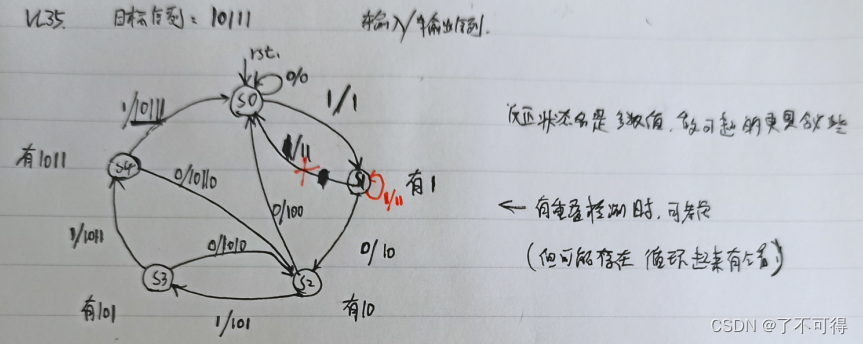
【24】Verilog进阶 - 序列检测2
VL35 状态机-非重叠的序列检测 1 思路 状态机嘛,也是比较熟悉的朋友啦, 我就火速写出了STG。如下黑色所示: 2 初版代码 `timescale 1ns/1nsmodule sequence_test1(input wire clk ,input wire rst ,input wire data ,output reg flag ); //*************code**********…...

详解线段树 ---更新查询
目录 一.问题引入 二.线段树 1.什么是线段树 2.线段树的举例 三.构建线段树 1.思路分析 2.代码实现 四.更新 1.思路分析 2.代码实现 五.查询 1.思路分析 2.代码实现 一.问题引入 有n个整数的数组,我们要 求解下标从left到right的元素之和为多少(query操作),然后还…...

【C语言进阶:刨根究底字符串函数】strncpy、strncat、strncmp函数
再前几篇的博客中大家可能发现了,strcpy,strcat,strcmp 这三个函数在使用时对源字符串没有长度限制,几乎是将源字符串的内容全部进行操作。在VS编译器中的这些函数显得不安全了,因此VS会提醒你在其后加上 _s &#x…...

计算机面试常见问答题目
英语口语 自我介绍 Hello, teachers. My name is Wang Xu. I come from Ningxia. I graduated from the School of Computer Science, Xi an Jiaotong University, majoring in Internet of Things. Next, I will introduce myself from four aspects. First of all, I studi…...
mac pro m1:安装dump文件内存分析工具——MAT
0. 引言 本文主要针对mac m1下安装Jprofiler进行讲解,安装核心步骤同样适用于其他系统 1. 安装 如果使用的是eclipse可以在插件中直接安装MAT,因为我使用的是idea开发,所以选择独立安装MAT工具 1、下载地址:https://www.eclip…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

生产管理系统开发:专业软件开发公司的实践与思考
生产管理系统开发的关键点 在当前制造业智能化升级的转型背景下,生产管理系统开发正逐步成为企业优化生产流程的重要技术手段。不同行业、不同规模的企业在推进生产管理数字化转型过程中,面临的挑战存在显著差异。本文结合具体实践案例,分析…...

Gitlab + Jenkins 实现 CICD
CICD 是持续集成(Continuous Integration, CI)和持续交付/部署(Continuous Delivery/Deployment, CD)的缩写,是现代软件开发中的一种自动化流程实践。下面介绍 Web 项目如何在代码提交到 Gitlab 后,自动发布…...
