最快方法求最长上升子序列(LIS)+最长公共子序列(LCS)模板(C/C++)
目录
1 LIS算法(最长上升子序列)
1.1 简介
1.2 代码
1.3 相关解释
2 LCS算法(最长公共子序列)
2.1 简介
2.2 代码(动态规划,时间复杂度O(nlogn))
2.3 特殊情况下的优化
1 LIS算法(最长上升子序列)
1.1 简介
LIS(Longest Increasing Subsequence)最长上升子序列
一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N。
比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8).
你的任务,就是对于给定的序列,求出最长上升子序列的长度。
1.2 代码
#include <bits/stdc++.h>
using namespace std;int a[99999],dp[99999]; // a数组为数据,dp[i]表示长度为i+1的LIS结尾元素的最小值int main()
{int n;while(cin>>n)//**解释1** {for(int i=0; i<n; i++){cin>>a[i];dp[i]=INT_MAX; // 初始化为无限大}int pos=0; // 记录dp当前最后一位的下标dp[0]=a[0]; // dp[0]值显然为a[0]for(int i=1; i<n; i++){if(a[i]>dp[pos]) // 若a[i]大于dp数组最大值,则直接添加dp[++pos] = a[i];else // 否则找到dp中第一个大于等于a[i]的位置,用a[i]替换之。dp[lower_bound(dp,dp+pos+1,a[i])-dp]=a[i]; // 二分查找**解释2** }cout<<pos+1<<endl;}return 0;
}1.3 相关解释
解释1:循环用例
假设我们根据给定的数字a和b,计算a与b的和。
如果使用这段代码:
#include <iostream>using namespace std;int main(){int a, b;cin >> a >> b;cout << a + b << endl;return 0;
}
则只能输入一组a和b,计算结束后程序就会退出。想要再计算一组和,需要重新运行程序。
如果使用循环用例:
#include <iostream>using namespace std;int main(){int a, b;while(cin >> a >> b){cout << a + b << endl;}return 0;
}
则可以处理多组输入,并且返回多组输出。
解释2:二分法找第一个大于/小于某个数的函数
lower_bound( )和upper_bound( )都是利用二分查找的方法在一个排好序的数组中进行查找的。
在从小到大的排序数组中,
lower_bound( begin,end,num):从数组的[begin,end)二分查找第一个大于或等于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
upper_bound( begin,end,num):从数组的[begin,end)二分查找第一个大于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
2 LCS算法(最长公共子序列)
2.1 简介
LCS是Longest Common Subsequence的缩写,即最长公共子序列。一个序列,如果是两个或多个已知序列的子序列,且是所有子序列中最长的,则为最长公共子序列。
比如,对于char x[]="aabcd";有顺序且相互相邻的aabc是其子序列,有顺序但是不相邻的abc也是其公共子序列。即,只要得出序列中各个元素属于所给出的数列,就是子序列。
再加上char y[]="12abcabcd";对比出才可以得出最长公共子序列abcd。
2.2 代码(动态规划,时间复杂度O(n*n))
#include<bits/stdc++.h>
using namespace std;int DP[1000][1000];
int LCS_length(string a, string b)//长度
{int M = a.size();int N = b.size();for(int i=1; i<=M; i++){for(int j=1; j<=N; j++){if(a[i-1] == b[j-1]) DP[i][j] = DP[i-1][j-1] + 1;//最好 else if(DP[i-1][j] >= DP[i][j-1]) DP[i][j] = DP[i-1][j];else DP[i][j] = DP[i][j-1];}}return DP[M][N];
}void LCS(string a, string b, int i, int j)//具体公共字符串
{if(i==0 || j==0) return;//设置边界 if(a[i-1]==b[j-1]){LCS(a, b, i-1, j-1);cout<<a[i-1]; }else if(DP[i-1][j] > DP[i][j-1]) LCS(a, b, i-1, j);else LCS(a, b, i, j-1);
}int main()
{string a, b;cout<<"请输入两个字符串:"<<endl;while(cin>>a>>b && a!="#"){cout<<"最大公共子序列长度为:"<<LCS_length(a, b)<<endl;cout<<"最大公共子序列为:";LCS(a, b, a.size(), b.size());cout<<endl<<"请输入两个字符串:"<<endl;}return 0;
}2.3 特殊情况下的优化(映射,时间复杂度O(nlogn))
特殊情况:一个序列没有重复元素,另一个序列随意
#include<bits/stdc++.h> //一个序列所有元素都不重复
using namespace std;
map <int,int> ma;
int n,m;
int s1[300009],s2[300009];
int a[300009],low[300009],len;int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>s1[i];for(int i=1;i<=m;i++)cin>>s2[i];for(int i=1;i<=m;i++)ma[s2[i]]=i;for(int i=1;i<=n;i++)a[i]=ma[s1[i]];int t=1;while(a[t]==0) t++;low[++len]=a[t];for(int i=2;i<=n;i++){if(a[i]==0) continue;if(a[i]>low[len])low[++len]=a[i];else{low[upper_bound(low+1,low+len+1,a[i])-low]=a[i];//自带函数}} printf("%d",len);return 0;
}相关文章:
+最长公共子序列(LCS)模板(C/C++))
最快方法求最长上升子序列(LIS)+最长公共子序列(LCS)模板(C/C++)
目录 1 LIS算法(最长上升子序列) 1.1 简介 1.2 代码 1.3 相关解释 2 LCS算法(最长公共子序列) 2.1 简介 2.2 代码(动态规划,时间复杂度O(nlogn)) 2.3 特殊…...
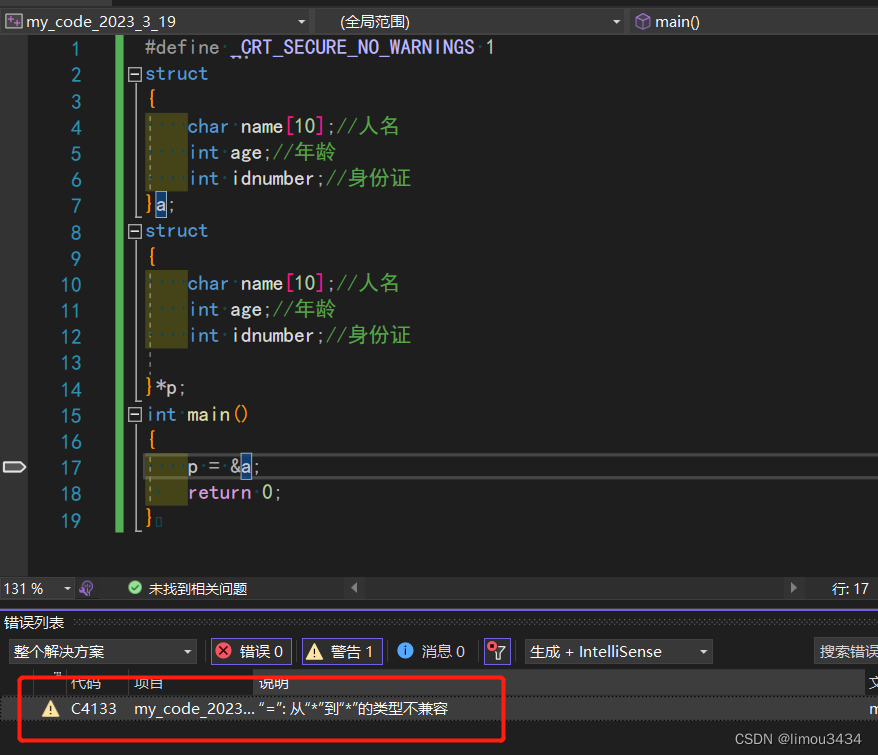
012+limou+C语言深入知识——(4)“结构体”与“枚举体”与“联合体”
一、结构体 1、结构体基础 (1)结构体完全声明 struct tag {member-list; }variable-list;//描述一个人 struct people {char name[10];//人名int age;//年龄int idnumber;//身份证 };(2)结构体不完全声明(匿名结构体…...

Canvas百战成神-圆(1)
Canvas百战成神-圆 初始化容器 <canvas id"canvas"></canvas>canvas{border: 1px solid black; }让页面占满屏幕 *{margin: 0;padding: 0; } html,body{width: 100%;height: 100%;overflow: hidden; } ::-webkit-scrollbar{display: none; }初始化画笔…...

详解分库分表设计
详解分库分表设计 背景 在传统的单机数据库架构中,所有数据都存储在同一个数据库中,随着业务规模的不断扩大,数据量和并发量也会越来越大,这会给数据库的性能和可用性带来挑战。此外,当单机数据库的容量达到瓶颈时…...
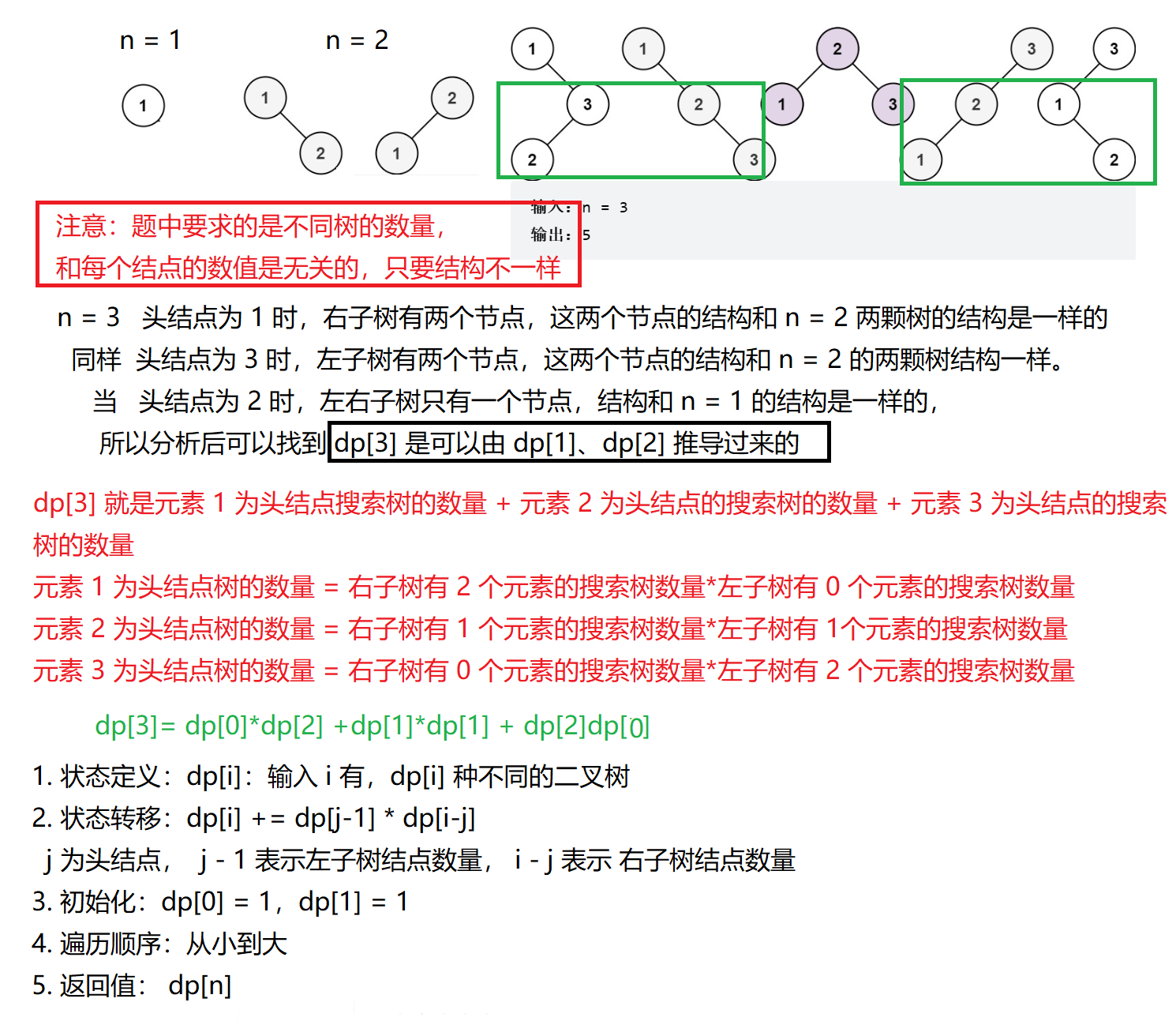
动态规划-基础(斐波那契数、爬楼梯、使用最小花费爬楼梯、不同路径、不同路径II、整数拆分、不同的二叉搜索树)
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的。动态规划问题,五步走:状态定义&am…...
深入理解WebSocket协议
“ 一直以来对WebSocket仅停留在使用阶段,也没有深入理解其背后的原理。当看到 x x x was not upgraded to websocket,我是彻底蒙了,等我镇定下来,打开百度输入这行报错信息,随即看到的就是大家说的跨域,或…...
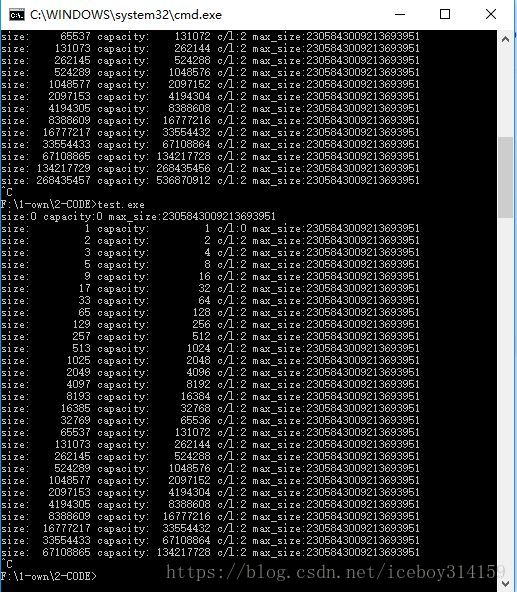
Vector的扩容机制
到需要扩容的时候,Vector会根据需要的大小,创建一个新数组,然后把旧数组的元素复制进新数组。 我们可以看到,扩容后,其实是一个新数组,内部元素的地址已经改变了。所以扩容之后,原先的迭代器会…...
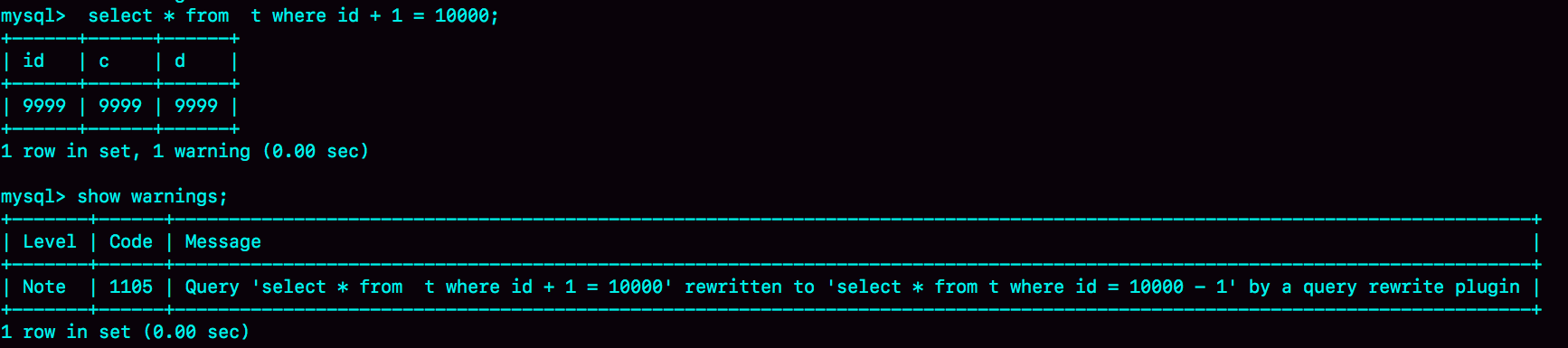
22讲MySQL有哪些“饮鸩止渴”提高性能的方法
短连接风暴 是指数据库有很多链接之后只执行了几个语句就断开的客户端,然后我们知道数据库客户端和数据库每次连接不仅需要tcp的三次握手,而且还有mysql的鉴权操作都要占用很多服务器的资源。话虽如此但是如果连接的不多的话其实这点资源无所谓的。 但是…...
10.0自定义SystemUI下拉状态栏和通知栏视图(六)之监听系统通知
1.前言 在进行rom产品定制化开发中,在10.0中针对systemui下拉状态栏和通知栏的定制UI的工作开发中,原生系统的下拉状态栏和通知栏的视图UI在产品开发中会不太满足功能, 所以根据产品需要来自定义SystemUI的下拉状态栏和通知栏功能,首选实现的就是下拉通知栏左滑删除通知的部…...
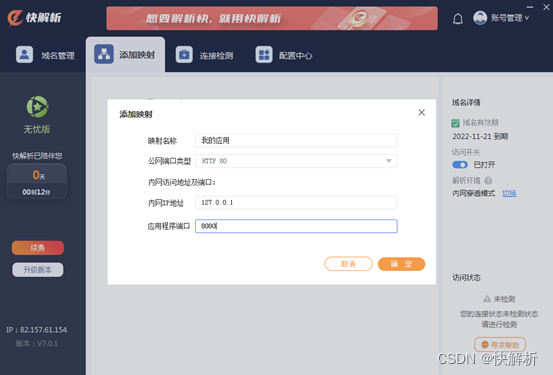
怎样在外网登录访问CRM管理系统?
一、什么是CRM管理系统? Customer Relationship Management,简称CRM,指客户关系管理,是企业利用信息互联网技术,协调企业、顾客和服务上的交互,提升管理服务。为了企业信息安全以及使用方便,企…...
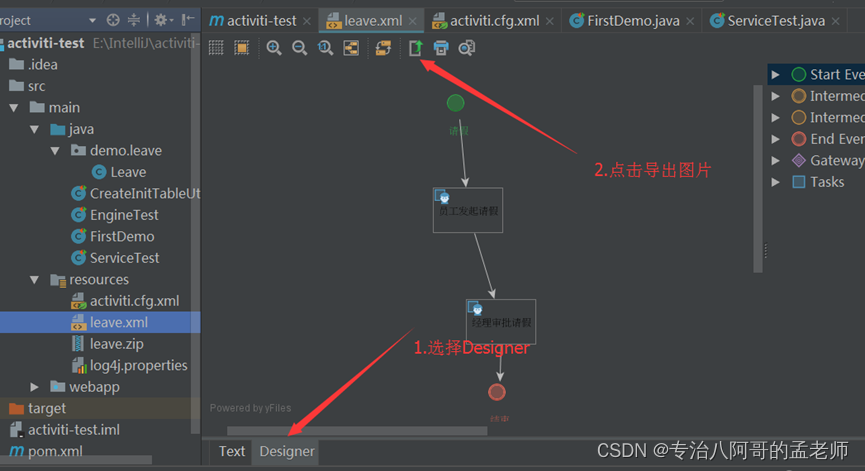
Activity工作流(三):Service服务
3. Service服务 所有的Service都通过流程引擎获得。 3.1 RepositoryService 仓库服务是存储相关的服务,一般用来部署流程文件,获取流程文件(bpmn和图片),查询流程定义信息等操作,是引擎中的一个重要的服务。…...

算法--最长回文子串--java--python
这个算法题里面总是有 暴力解法 把所有字串都拿出来判断一下 这里有小小的优化: 就是当判断的字串小于等于我们自己求得的最长回文子串的长度,那么我们就不需要在进行对这个的判断这里的begin,还可以用来取得最小回文子串是什么 java // 暴…...
ElasticSearch-第二天
目录 文档批量操作 批量获取文档数据 批量操作文档数据 DSL语言高级查询 DSL概述 无查询条件 叶子条件查询 模糊匹配 match的复杂用法 精确匹配 组合条件查询(多条件查询) 连接查询(多文档合并查询) 查询DSL和过滤DSL 区别 query DSL filter DSL Query方式查…...
【AI大比拼】文心一言 VS ChatGPT-4
摘要:本文将对比分析两款知名的 AI 对话引擎:文心一言和 OpenAI 的 ChatGPT,通过实际案例让大家对这两款对话引擎有更深入的了解,以便大家选择合适的 AI 对话引擎。 亲爱的 CSDN 朋友们,大家好!近年来&…...

美团笔试-3.18
1、捕获敌人 小美在玩一项游戏。该游戏的目标是尽可能抓获敌人。 敌人的位置将被一个二维坐标 (x, y) 所描述。 小美有一个全屏技能,该技能能一次性将若干敌人一次性捕获。 捕获的敌人之间的横坐标的最大差值不能大于A,纵坐标的最大差值不能大于B。 现在…...

【12】SCI易中期刊推荐——计算机信息系统(中科院4区)
🚀🚀🚀NEW!!!SCI易中期刊推荐栏目来啦 ~ 📚🍀 SCI即《科学引文索引》(Science Citation Index, SCI),是1961年由美国科学信息研究所(Institute for Scientific Information, ISI)创办的文献检索工具,创始人是美国著名情报专家尤金加菲尔德(Eugene Garfield…...

好不容易约来了一位程序员来面试,结果人家不做笔试题
感觉以后还是不要出面试题这环节好了。好不容易约来了一位程序员来面试。刚递给他一份笔试题,他一看到要做笔试题,说不做笔试题,有问题面谈就好了,搞得我有点尴尬,这位应聘者有3年多工作经验。关于程序员岗位ÿ…...

这几个过时Java技术不要再学了
Java 已经发展了近20年,极其丰富的周边框架打造了一个繁荣稳固的生态圈。 Java现在不仅仅是一门语言,而且还是一整个生态体系,实在是太庞大了,从诞生到现在,有无数的技术在不断的推出,也有很多技术在不断的…...

EEPROM芯片(24c02)使用详解(I2C通信时序分析、操作源码分析、原理图分析)
1、前言 (1)本文主要是通过24c02芯片来讲解I2C接口的EEPROM操作方法,包含底层时序和读写的代码; (2)大部分代码是EEPROM芯片通用的,但是其中关于某些时间的要求,是和具体芯片相关的,和主控芯片和外设芯片都有关系&…...
Django4.0新特性-主要变化
Django 4.0于2021年12月正式发布,标志着Django 4.X时代的来临。参考Django 4.0 release notes | Django documentation | Django Python 兼容性 Django 4.0 将支持 Python 3.8、3.9 与 3.10。强烈推荐并且仅官方支持每个系列的最新版本。 Django 3.2.x 系列是最后…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...
