递归与递推
递归
- 直白理解:函数在其内部调用自身(自己调用自己)
- 所有递归都可以采用递归搜索树来理解
- 递归的特点:
- 一般来说代码较为简短,但是理解难度大
- 一般时间和空间消耗较大,容易产生重复计算,可能爆栈
递归实现指数型枚举
题目描述
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1 <= n <= 15
输入样例
3
输出样例
32
2 3
1
1 3
1 2
1 2 3
思路:递归(DFS)
-
从1 ~ n依次参考每一个数,选或者不选。
-
举个栗子:
当n = 2时
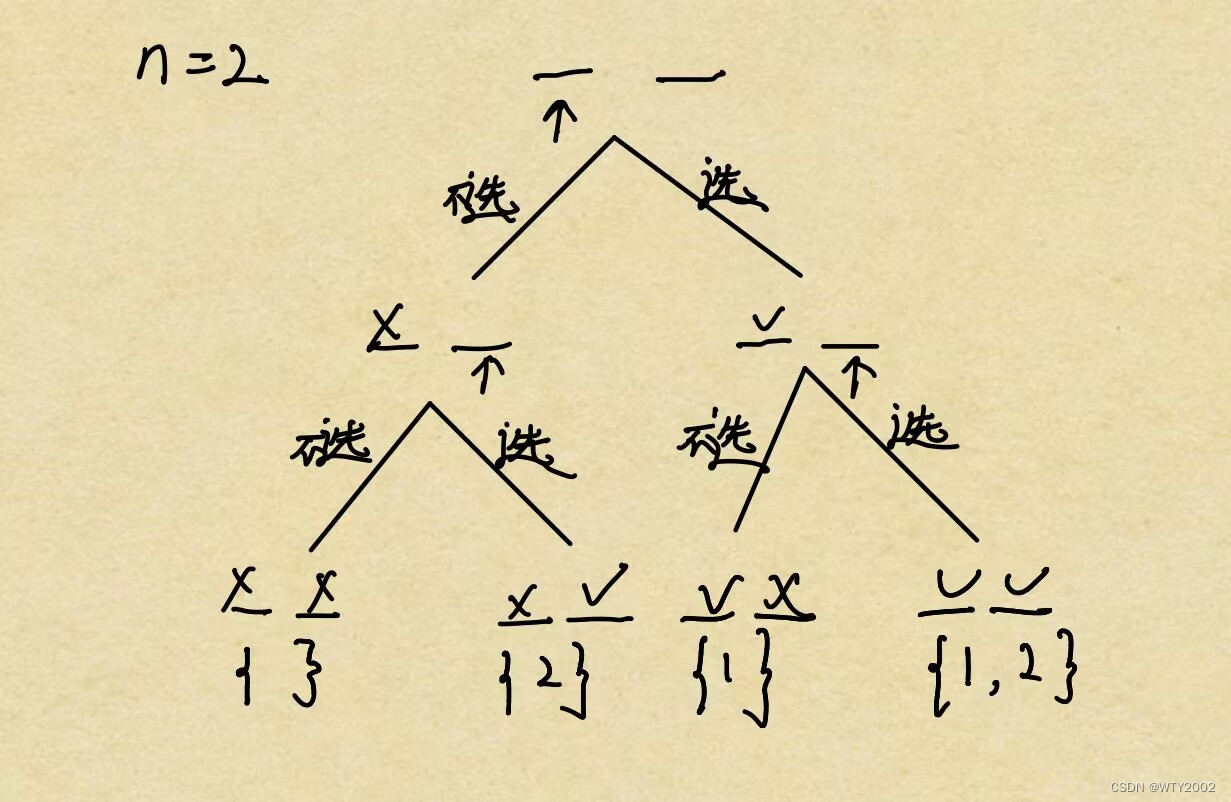
从1~n依次考虑这个数选或者不选。
AC代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 16;int n;
int nums[N]; //记录当前位置的状态,0:还没考虑,1:选它,2:不选它 void dfs(int curr) {if (curr > n) {for (int i = 1; i <= n; i++) { //if (nums[i] == 1) {cout << i << " ";}}cout << endl;return;}nums[curr] = 2; //当前位置不选dfs(curr + 1); // 第一个分支:不选当前位置nums[curr] = 0; // 恢复现场,此处该语句可省略nums[curr] = 1; //当前位置选dfs(curr + 1); // 第二个分支:选当前位置nums[curr] = 0; // 恢复现场,此处该语句可省略
}int main()
{cin >> n;dfs(1); //传入当前枚举的位置,从第一位开始枚举return 0;
}
变式:将所有方案记录下来
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>using namespace std;const int N = 16;int n;
int nums[N]; //记录当前位置的状态,0:还没考虑,1:选它,2:不选它
vector<vector<int> > ways; //用来记录每一个方案void dfs(int curr) {if (curr > n) {vector<int> way;for (int i = 1; i <= n; i++) { //记录方案if (nums[i] == 1) {way.push_back(i);}}ways.push_back(way);return;}nums[curr] = 2; //当前位置不选dfs(curr + 1); // 第一个分支:不选当前位置nums[curr] = 0; // 恢复现场,此处该语句可省略nums[curr] = 1; //当前位置选dfs(curr + 1); // 第二个分支:选当前位置nums[curr] = 0; // 恢复现场,此处该语句可省略
}int main()
{scanf("%d", &n);dfs(1); //传入当前枚举的位置,从第一位开始枚举for (int i = 0; i < ways.size(); i++) {for (int j = 0; j < ways[i].size(); j++) {printf("%d ", ways[i][j]);}puts("");}return 0;
}
递归实现排列型枚举
题目描述
把 1∼n 这 n 个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式
一个整数 n。
输出格式
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围
1 <= n <= 9
输入样例
3
输出样例
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
思路:递归(DFS)
全排列问题有两种理解思路:
-
顺序一:依次枚举每个数放到哪个位置
-
顺序二:依次枚举每个位置放哪个数
以顺序二为例:
当n = 3时:
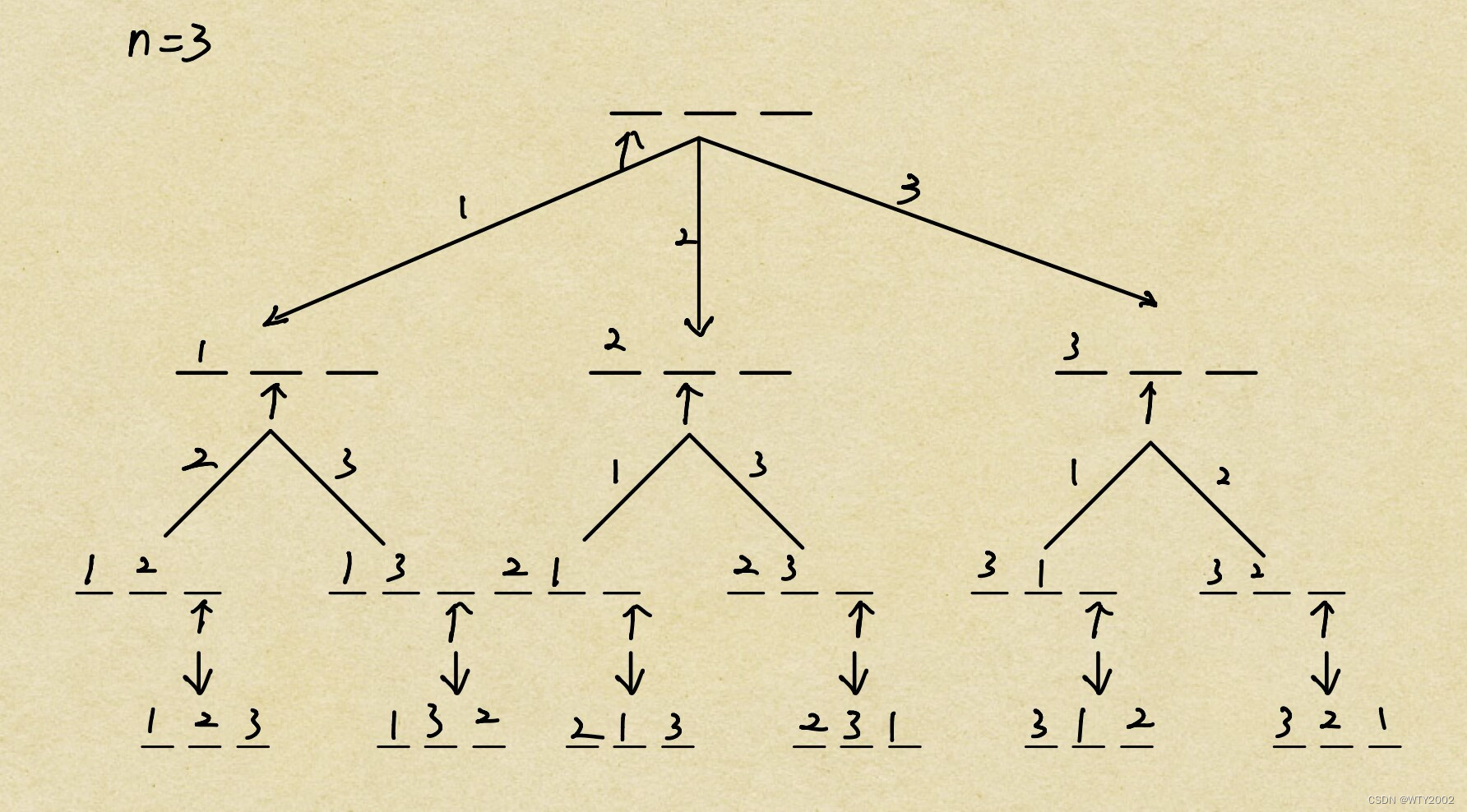
AC代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 10;int n;
int state[N]; //记录当前方案;0表示还没放数; 1~n表示放入的数字
bool used[N]; //记录当前的数是否被使用;true:使用过; false:还未使用void dfs(int curr) {if (curr > n) { //判断边界for (int i = 1; i <= n; i++) { //输出方案printf("%d ", state[i]);}puts("");return;}//一次枚举每个分支,即当前位置可以填哪些数for (int i = 1; i <= n; i++) { //按字典序从小到大一次枚举if (!used[i]) {state[curr] = i; //填入该数used[i] = true; //记录该数已被选用dfs(curr + 1); //枚举下一个位置//恢复现场state[curr] = 0; //该语句此处可以省略used[i] = false;}}
}int main()
{cin >> n;dfs(1); //传入当前枚举的位置,从第一位开始枚举return 0;
}
递归实现组合型枚举
题目描述
把 1∼n 这 n 个整数中随机选出 m 个,输出所有可能的选择方案。
输入格式
两个整数 n,m在同一行用空格隔开。
输出格式
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行内的数升序排列,相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如 1 3 5 7 排在 1 3 6 8 前面)
数据范围
n > 0,
0 <= m <= n,
n + (n - m) <= 25
输入样例
5 3
输出样例
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
思路:递归(DFS)
- 题目要求是组合型枚举
- 不能含重复项
- 每一组数据从小到大排列
当n = 5,m = 3时,仅有以下几种符合要求:(其余分支无法凑满3个数,因此舍弃)
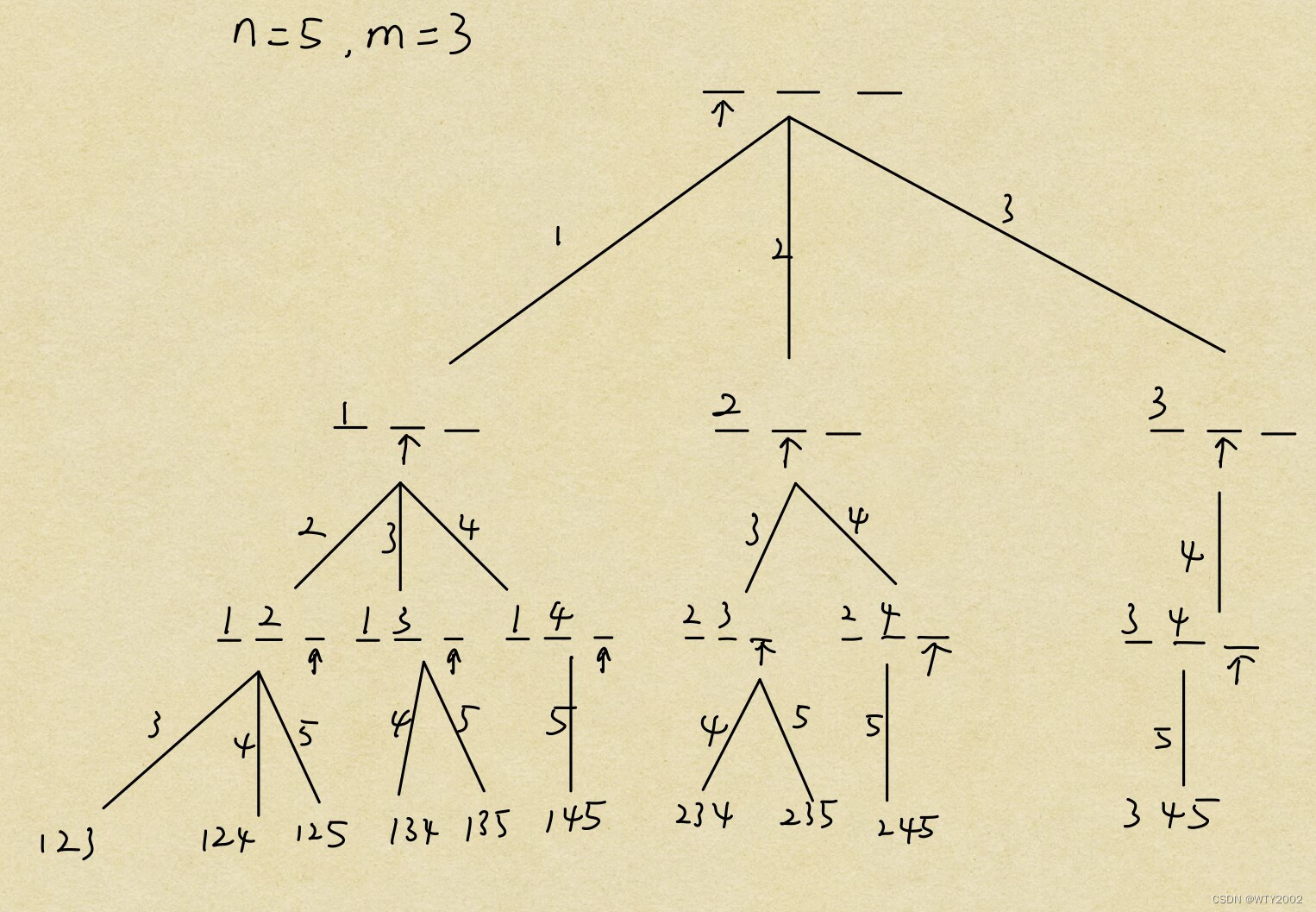
在枚举每个位置的时候,将数字从小到大枚举(这里考虑局部属性,只需保证新加的数大于前一个数)
考虑需要的参数:(全局变量、形参)
- 参数一:m个位置,用来存入数据。way[N]
- 参数二:当前枚举到哪个位置。curr
- 参数三:当前最小可以从哪个数开始枚举。start
AC代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 30;int n, m;
int way[N]; //用来记录当前方案。0表示还未放入数据;1~n表示存入的数据void dfs(int curr, int start) {if (curr == m + 1) { //边界判断,已经选了m个数for (int i = 1; i <= m; i++) { //输出方案printf("%d ", way[i]);}puts("");return;}for (int i = start; i <= n; i++) { //每次从start开始枚举,保证后一个数比前一个数大way[curr] = i; //将数据i放入当前位置dfs(curr + 1, i + 1);way[curr] = 0; //回复现场,此处可以省略}
}int main()
{scanf("%d%d", &n, &m);dfs(1,1); //第一个参数:从第一个位置开始枚举。第二个参数:最小可以从1开始枚举return 0;
}
剪枝优化
- 当枚举到第curr个位置时,表示正在选第curr个数,此时已经选好了curr - 1个数
- 剩下可供选择的数为从start到n,共有n - start + 1
- 当选中的数和剩下的所有数加起来不够m个数时,表示此方案无解,可以提前舍弃。
- curr - 1 + n - start + 1 < m**(即curr + n - start < m)**
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 30;int n, m;
int way[N]; //用来记录当前方案。0表示还未放入数据;1~n表示存入的数据void dfs(int curr, int start) {//剪枝,当后面的所有数加起来不够m个时,直接返回if (curr + n - start < m) {return;}if (curr == m + 1) { //边界判断,已经选了m个数for (int i = 1; i <= m; i++) {printf("%d ", way[i]);}puts("");return;}for (int i = start; i <= n; i++) { //每次从start开始枚举,保证后一个数比前一个数大way[curr] = i; //将数据i放入当前位置dfs(curr + 1, i + 1);way[curr] = 0; //回复现场,此处可以省略}
}int main()
{scanf("%d%d", &n, &m);dfs(1,1); //第一个参数:从第一个位置开始枚举。第二个参数:最小可以从1开始枚举return 0;
}
带分数
题目描述
100 可以表示为带分数的形式:100 = 3 + 6925871469258 \over 71471469258
还可以表示为:100 = 82 + 35461973546 \over 1971973546
注意特征:带分数中,数字 1∼9
分别出现且只出现一次(不包含 0)。
类似这样的带分数,100有11种表示法。
输入格式
一个正整数n。
输出格式
输出输入数字用数码 1∼9 不重复不遗漏地组成带分数表示的全部种数。
数据范围
1 <= N < 10610^6106
输入样例1:
100
输出样例1:
11
输入样例2:
105
输出样例2:
6
思路:递归(DFS)
上述等式可以表示为这种形式:n = a + bcb \over ccb,采取一下方案来解决问题:
- 枚举a、b、c的全排列
- 分别枚举a、b、c的位数
- 判断等式是否成立
- 结合题目优化一下:
- 将上述等式转变为:c * n = c * a + b
- n已知,分别枚举a和c的全排列,然后计算b是否满足要求即可。
AC代码
#include<bits/stdc++.h>
using namespace std;const int N = 20;
int n, ans; //ans用来记录最终的种数
bool st[N], backup[N]; // st数组记录当前数字是否被使用过。ture:表示使用过;false:表示未使用;backup数组用来备份stbool check(int a, int c) {long long b = n * (long long)c - a * c;if (!a || !b || !c) return false; //a,b,c均不能为0memcpy(backup, st, sizeof st); //备份st数组while (b) {int x = b % 10; //取个位数b /= 10; //删除个位数if (!x || backup[x]) return false; //依次判断b的每一个数是否被使用过backup[x] = true; //标记这个数被用过}for (int i = 1; i <= 9; i++) { //判断9个数是否都被使用过if (!backup[i]) return false;}return true;
}void dfs_c(int used, int a, int c) { // 第一个参数表示:当前已经用了多少个数字;第二个参数表示a的值;第三个参数表示c的值if (used >= n) return; //如果已经用完了n个数字,则返回if(check(a,c)) ans++; //检验a和c是否满足要求for (int i = 1; i <= 9; i++) {if (!st[i]) {st[i] = true;dfs_c(used + 1, a, c * 10 + i);st[i] = false; //恢复现场}}
}void dfs_a(int used, int a) { //第一个参数表示:当前已经用了多少个数字;第二个参数表示a的值if (a >= n) return; //如果a >= n则无解,直接返回if (a) dfs_c(used, a, 0);for (int i = 1; i <= 9; i++) {if (!st[i]) {st[i] = true;dfs_a(used + 1, a * 10 + i);st[i] = false; //恢复现场}}
}int main() {cin >> n;dfs_a(0, 0); //第一个参数表示:当前已经用了多少个数字;第二个参数表示a的值cout << ans;return 0;
}
剪枝优化
- 在枚举a的位数的时候,已经使用的数最多达到7,因为b和c至少各占一位
- 在枚举c的时候,已经使用的数最多达到8,因为b至少占一位
#include<bits/stdc++.h>
using namespace std;const int N = 20;
int n, ans; //ans用来记录最终的种数
bool st[N], backup[N]; // st数组记录当前数字是否被使用过。ture:表示使用过;false:表示未使用;backup数组用来备份stbool check(int a, int c) {long long b = n * (long long)c - a * c;if (!a || !b || !c) return false; //a,b,c均不能为0memcpy(backup, st, sizeof st); //备份st数组while (b) {int x = b % 10; //取个位数b /= 10; //删除个位数if (!x || backup[x]) return false; //依次判断b的每一个数是否被使用过backup[x] = true; //标记这个数被用过}for (int i = 1; i <= 9; i++) { //判断9个数是否都被使用过if (!backup[i]) return false;}return true;
}void dfs_c(int used, int a, int c) { // 第一个参数表示:当前已经用了多少个数字;第二个参数表示a的值;第三个参数表示c的值if (used >= 8) return; //剪枝优化,当used = 8时就可以返回了,因为b至少占一位if(check(a,c)) ans++; //检验a和c是否满足要求for (int i = 1; i <= 9; i++) {if (!st[i]) {st[i] = true;dfs_c(used + 1, a, c * 10 + i);st[i] = false; //恢复现场}}
}void dfs_a(int used, int a) { //第一个参数表示:当前已经用了多少个数字;第二个参数表示a的值if (a >= n) return; //如果a >= n则无解,直接返回if (used >= 7) return; //剪枝优化,当used = 7时就可以返回了,因为b和c至少各占一位if (a) dfs_c(used, a, 0); //当a不等于0的时候再去枚举c的可能情况for (int i = 1; i <= 9; i++) {if (!st[i]) {st[i] = true;dfs_a(used + 1, a * 10 + i);st[i] = false; //恢复现场}}
}int main() {cin >> n;dfs_a(0, 0); //第一个参数表示:当前已经用了多少个数字;第二个参数表示a的值cout << ans;return 0;
}
递推
简单斐波那契
题目描述
以下数列0 1 1 2 3 5 8 13 21 … 被称为斐波纳契数列。
这个数列从第 3 项开始,每一项都等于前两项之和。
输入一个整数 N,请你输出这个序列的前 N 项。
输入格式
一个整数 N。
输出格式
在一行中输出斐波那契数列的前 N 项,数字之间用空格隔开。
数据范围
0 < N < 46
输入样例:
5
输出样例:
0 1 1 2 3
思路:递推
- 根据数列的规律可知,数列的每一项等于其前面两项之和
- 即:f(n) = f(n - 1) + f(n - 2); (n >= 3)
AC代码
#include<bits/stdc++.h>
using namespace std;int main()
{int n, a = 0, b = 1, t;cin >> n;for (int i = 1; i <= n; i++) {cout << a << " ";t = a + b;a = b;b = t;}return 0;
}
费解的开关
题目描述
你玩过“拉灯”游戏吗?
25 盏灯排成一个 5×5 的方形。
每一个灯都有一个开关,游戏者可以改变它的状态。
每一步,游戏者可以改变某一个灯的状态。
游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字 1 表示一盏开着的灯,用数字 0 表示关着的灯。
下面这种状态
10111
01101
10111
10000
11011
在改变了最左上角的灯的状态后将变成:
01111
11001
11001
10100
11011
给定一些游戏的初始状态,编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。
输入格式
第一行输入正整数 n,代表数据中共有 n 个待解决的游戏初始状态。
以下若干行数据分为 n 组,每组数据有 5 行,每行 5 个字符。
每组数据描述了一个游戏的初始状态。
各组数据间用一个空行分隔。
输出格式
一共输出 n 行数据,每行有一个小于等于 6 的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若 6 步以内无法使所有灯变亮,则输出 −1。
数据范围
0 < N <= 500
输入样例:
3
00111
01011
10001
11010
1110011101
11101
11110
11111
1111101111
11111
11111
11111
11111
输出样例:
3
2
-1
思路:递推
结合题目分析可以得出以下性质:
- 按开关的顺序是随意的,没有影响
- 每个开关最多只按一次(要求最小的触发次数,按两次等于没按)
结论:
- 每一行开关的操作,完全由上一行灯的明灭状态所决定。(能影响第一行灯状态的只有第二行灯,以此类推)
- 每操作一行只能保证当前行的前面所有行的灯都亮着,当前行无法保证。
- 因此只需要枚举第一行的所有操作即可。共25 = 25种方案(利用二进制枚举)
AC代码
#include<bits/stdc++.h>
using namespace std;const int N = 6;
char nums[N][N], backup[N][N];
int dx[5] = {-1, 0, 1, 0, 0}, dy[5] = {0, 1, 0, -1, 0};void turn(int x, int y) { //改变上下左右和当前的灯for (int i = 0; i < 5; i++) {int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= 5 || b < 0 || b >= 5) {continue; //越界了}nums[a][b] ^= 1; //字符'0'变'1','1'变'0'}
}int main()
{int n;scanf("%d", &n);while (n--) {for (int i = 0; i < 5; i++) {scanf("%s", nums[i]);}int ans = 10;for (int i = 0; i < 32; i++) {memcpy(backup, nums, sizeof nums); //将nums数组备份int step = 0;for (int t = 0; t < 5; t++) {if (i >> t & 1) {step++;turn(0, t); //改变上下左右和当前的灯}}for (int x = 0; x < 4; x++) { //检查前4行灯for (int y = 0; y < 5; y++) {if (nums[x][y] == '0') { //如果当前位置的灯是灭的,则要按当前位置等的下一行灯的按钮step++;turn(x + 1, y); //改变上下左右和当前的灯}}}bool flag = false;for (int i = 0; i < 5; i++) { //检查最后一排灯是否都变亮if (nums[4][i] == '0') {flag = true;break;}}if (!flag) { //更新答案ans = min(ans, step);}memcpy(nums, backup, sizeof nums); //恢复nums数组}if (ans > 6) ans = -1;printf("%d\n", ans);}return 0;
}
翻硬币
题目描述
小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零)。
比如,可能情形是:**oo***oooo
如果同时翻转左边的两个硬币,则变为:oooo***oooo
现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
我们约定:把翻动相邻的两个硬币叫做一步操作。
输入格式
两行等长的字符串,分别表示初始状态和要达到的目标状态。
输出格式
一个整数,表示最小操作步数
数据范围
输入字符串的长度均不超过100。
数据保证答案一定有解。
输入样例1:
**********
o****o****
输出样例1:
5
输入样例2:
*o**o***o***
*o***o**o***
输出样例2:
1
思路:
我们可以依据输入输出样例来进行模拟分析,可以发现以下性质:
- 一次能改变一组相邻的两枚硬币,翻两次相当于没有改变。
- 对于同一个位置,如果初始态和目标太的硬币正反不一致,则含有该硬币的一组相邻硬币一定要进行翻转。
- 题目保证样例必有解,我们可以从左到右进行模拟,遇到不同的硬币就进行翻转,可以发现翻转硬币数最少的方案是唯一的。
AC代码
#include<bits/stdc++.h>
using namespace std;int main() {string s1, s2;cin >> s1 >> s2;int ans = 0;for (int i = 0; i < s1.size() - 1; i++) {if (s1[i] != s2[i]) { //当前位置硬币正反不同,需要进行翻转s1[i] = s2[i];s1[i + 1] = s1[i + 1] == '*' ? 'o' : '*';ans++;}}cout << ans;return 0;
}
飞行员兄弟
题目描述
“飞行员兄弟”这个游戏,需要玩家顺利的打开一个拥有 16 个把手的冰箱。
已知每个把手可以处于以下两种状态之一:打开或关闭。
只有当所有把手都打开时,冰箱才会打开。
把手可以表示为一个 4×4 的矩阵,您可以改变任何一个位置 [i,j] 上把手的状态。
但是,这也会使得第 i 行和第 j 列上的所有把手的状态也随着改变。
请你求出打开冰箱所需的切换把手的次数最小值是多少。
输入格式
输入一共包含四行,每行包含四个把手的初始状态。
符号 + 表示把手处于闭合状态,而符号 - 表示把手处于打开状态。
至少一个手柄的初始状态是关闭的。
输出格式
第一行输出一个整数 N,表示所需的最小切换把手次数。
接下来 N 行描述切换顺序,每行输出两个整数,代表被切换状态的把手的行号和列号,数字之间用空格隔开。
注意:如果存在多种打开冰箱的方式,则按照优先级整体从上到下,同行从左到右打开。
数据范围
1 <= i,j <= 4
输入样例1:
-+--
----
----
-+--
输出样例1:
5
输入样例2:
*o**o***o***
*o***o**o***
输出样例2:
6
1 1
1 3
1 4
4 1
4 3
4 4
思路:
经分析可知:
-
每一个控制把手最多按一次
-
按把手的先后顺序无关紧要
-
本题很难找出递推规律,因为影响一个冰箱门的开关太多了,因此可以采用暴力枚举来解决
-
枚举所有方案。0~216 - 1(二进制枚举)每个方案对应的位置如下:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
-
按照每一个枚举的方案,对冰箱进行对应的操作
-
判断方案是否符合要求
-
AC代码
#include<bits/stdc++.h>
using namespace std;const int N = 5;
char g[N][N], backup[N][N];int get(int x, int y) { //映射关系转换return x * 4 + y;
}void turn(int x, int y) { //将x,y所在位置的行和列的符号反转for (int i = 0; i < 4; i++) { //反转第x行的符号if (g[x][i] == '+') {g[x][i] = '-';} else {g[x][i] = '+';}}for (int i = 0; i < 4; i++) { //反转第y列的符号if (g[i][y] == '+') {g[i][y] = '-';} else {g[i][y] = '+';}}g[x][y] = g[x][y] == '+' ? '-' : '+';
}int main() {vector<pair<int, int>> ans; //用来存储当前最优的操作方案for (int i = 0; i < 4; i++) cin >> g[i];for (int i = 0; i < 1 << 16; i++) {vector<pair<int, int>> temp; //存储当前操作memcpy(backup, g, sizeof g); //备份//对当前方案进行检验for (int x = 0; x < 4; x++) {for (int y = 0; y < 4; y++) { //遍历矩阵if (i >> get(x,y) & 1) { //判断当前位置的开关是否被按temp.push_back({x, y});turn(x, y);}}}//判断所有冰箱是否都打开bool flag = true;for (int x = 0; x < 4; x++) {for (int y = 0; y < 4; y++) {if (g[x][y] == '+') {flag = false;}}}if (flag) {if (ans.empty() || ans.size() > temp.size()) { //记录操作次数最少的方案ans = temp;}}memcpy(g, backup, sizeof g); // 还原}cout << ans.size() << endl;for (int i = 0; i < ans.size(); i++) {cout << ans[i].first + 1 << " " << ans[i].second + 1 << endl;}return 0;
}
相关文章:

递归与递推
递归 直白理解:函数在其内部调用自身(自己调用自己)所有递归都可以采用递归搜索树来理解递归的特点: 一般来说代码较为简短,但是理解难度大一般时间和空间消耗较大,容易产生重复计算,可能爆栈 …...
使用<style scoped>导致的样式问题
问题描述: 今天使用开源组件库TDesign的自动补全组件时,遇到了一个样式失效问题,一开始怎么也找不到问题出在哪,后面一个偶然去掉了scoped,竟然发现样式竟然正常了,具体原因不知道在哪,有大佬知…...
-集群关键指标及调优指南)
Elasticsearch深入理解(十八)-集群关键指标及调优指南
1、CPU使用率 CPU使用率是指在一段时间内CPU执行程序的百分比,它是衡量系统资源利用率的一种指标。 1.1 详细说明: 在Elasticsearch中,高的CPU使用率通常意味着节点正在执行大量的计算任务,这可能是因为索引和搜索操作的负载较大…...
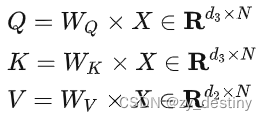
Transformer到底为何这么牛
从注意力机制(attention)开始,近两年提及最多的就是Transformer了,那么Transformer到底是什么机制,凭啥这么牛?各个领域都能用?一文带你揭开Transformer的神秘面纱。 目录 1.深度学习࿰…...

【Spring事务】声明式事务 使用详解
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 声明式事务一、编程式事务二、声明式事务&…...
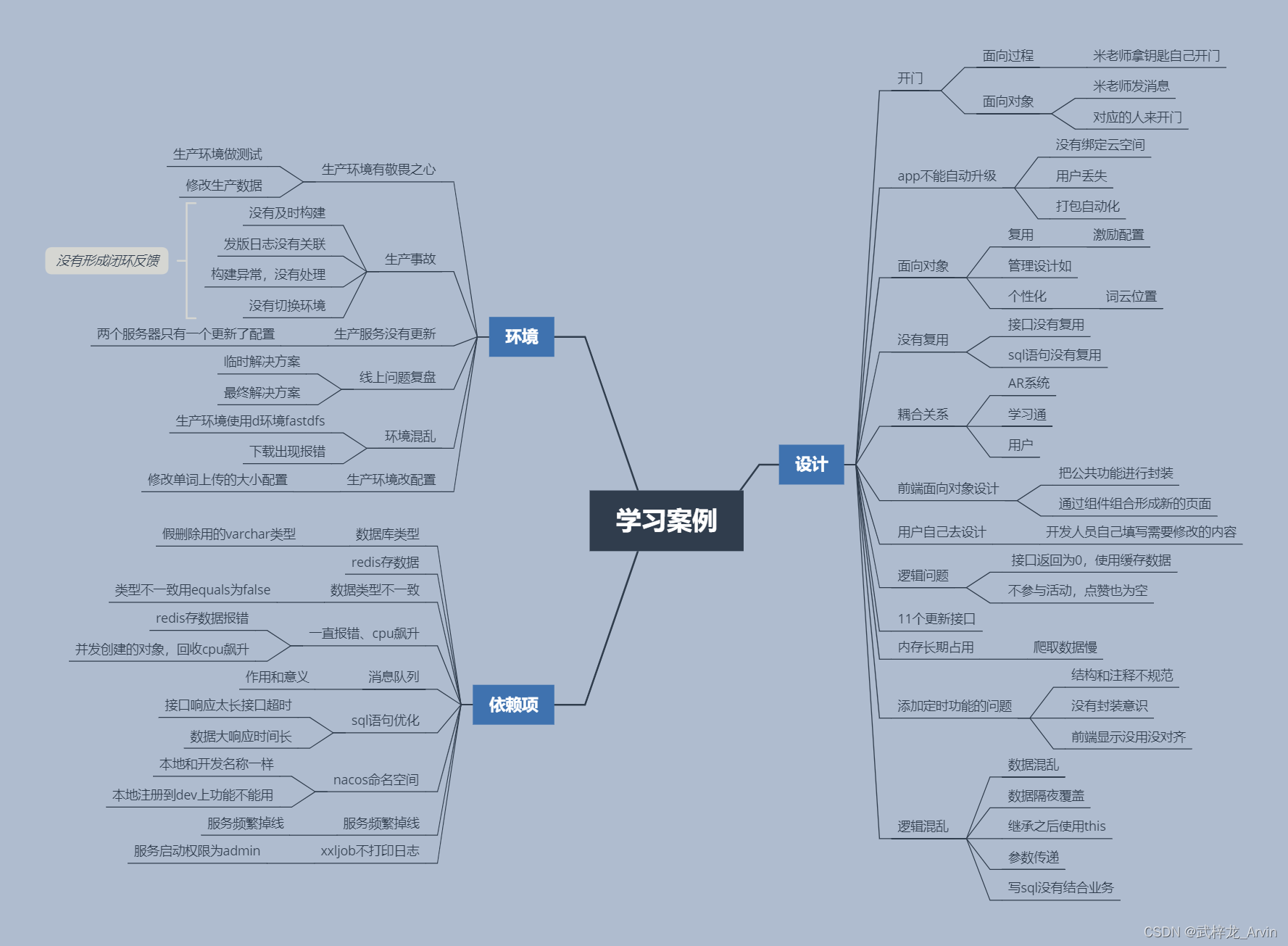
学习28个案例总结
学习前 对于之前遇到的问题没有及时总结,导致做什么事情都是新的一样。没有把之前学习到接触到的内容应用上。通过这次对28个案例的学习。把之前遇到的问题总结成自己的经验,在以后的开发过程中避免踩重复性的坑。多看帮助少走弯路。 学习中 对28个案例…...

刷题Java常用方法总结
刷题Java常用方法总结 文章目录刷题Java常用方法总结快速查看:静态数组 Static Array初始化instance属性length技巧Arrays.sort从小到大排序Arrays.fill填满一个数组Arrays.copyOf / arr.clone()复制一个数组(二维数组也可以)动态数组 List & Dynamic Array初始化常规 - Ar…...
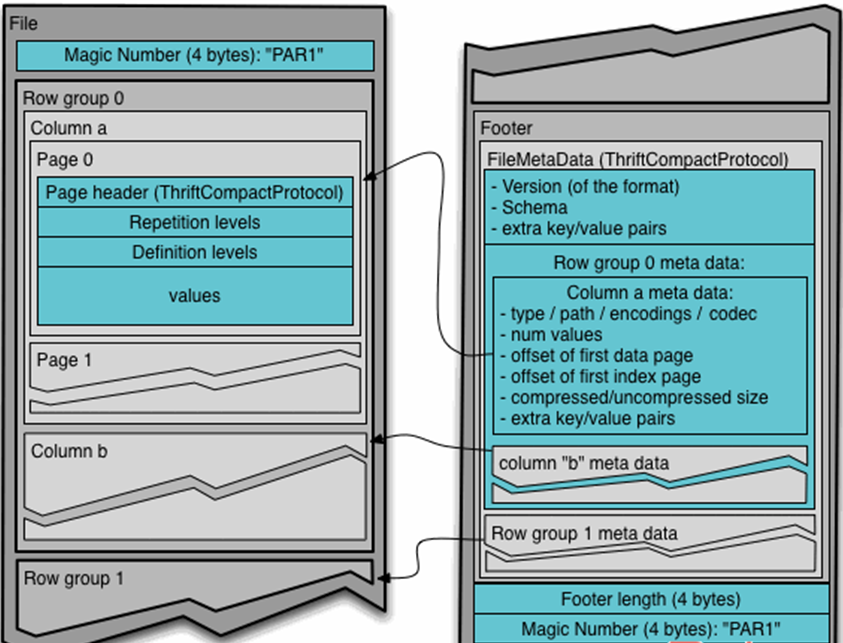
大数据技术之Hive
第1章Hive基本概念1.1 Hive1.1.1 Hive的产生背景在那一年的大数据开源社区,我们有了HDFS来存储海量数据、MapReduce来对海量数据进行分布式并行计算、Yarn来实现资源管理和作业调度。但是面对海量数据和负责的业务逻辑,开发人员要编写MR来对数据进行统计…...

第33篇:Java集合类框架总结
目录 1、集合概念 2、集合与数组的区别 3、集合框架的特性 1)高性能 2)可操作...
数据结构 | 栈的中缀表达式求值
目录 什么是栈? 栈的基本操作 入栈操作 出栈操作 取栈顶元素 中缀表达式求值 实现思路 具体代码 什么是栈? 栈是一种线性数据结构,具有“先进后出”(Last In First Out, LIFO)的特点。它可以看作是一种受限的…...
vue2前端实现html导出pdf功能
1. 功能实现方案 1.html转换成canvas后生成图片导出pdf(本文选用) html转canvas插件:html2canvas是一款将HTML代码转换成Canvas的插件;canvas生成pdf:jsPDF是一个使用Javascript语言生成PDF的开源库 2.HTML代码转出…...

用 ChatGPT 辅助学好机器学习
文章目录一、前言二、主要内容🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 探索更高效的学习方法可能是有志者共同的追求,用好 ChatGPT,先行于未来。 作为一个人工智能大语言模型,ChatGPT 可以在帮助初…...
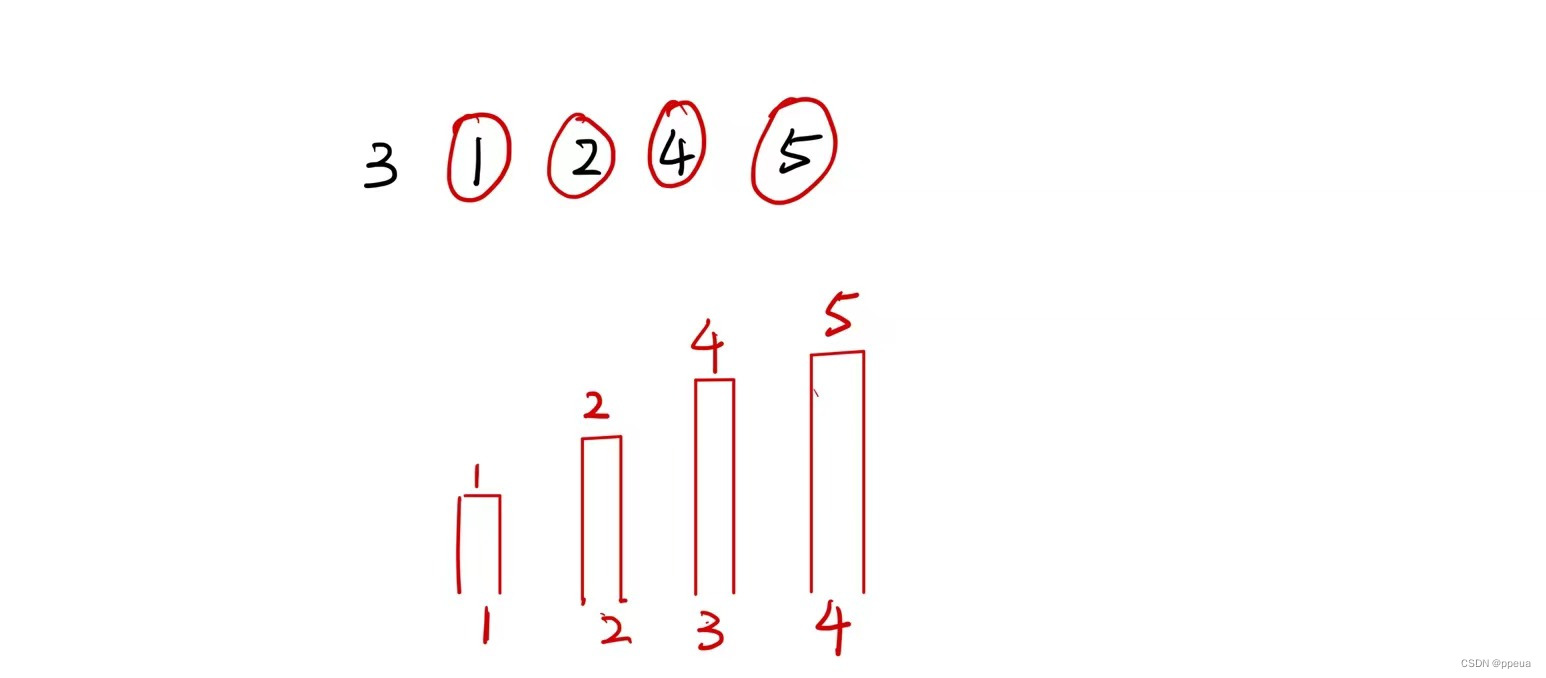
【动态规划】最长上升子序列(单调队列、贪心优化)
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
海思SD3403/SS928V100开发(7)mcp2515-SPI转CAN驱动开发
1. 前言 需求: 需要一路can进行收发 分析: 根据目前使用较多的方案是使用主控端SPI接口 接入MCP2515芯片进行CAN协议转换 硬件: MCP2515->SPI2->SS928 2. Uboot开发 2.1 pinmux复用配置 2.1.1 修改uboot参数表 路径: osdrv/tools/pc/uboot_tools/ SS928V100…...
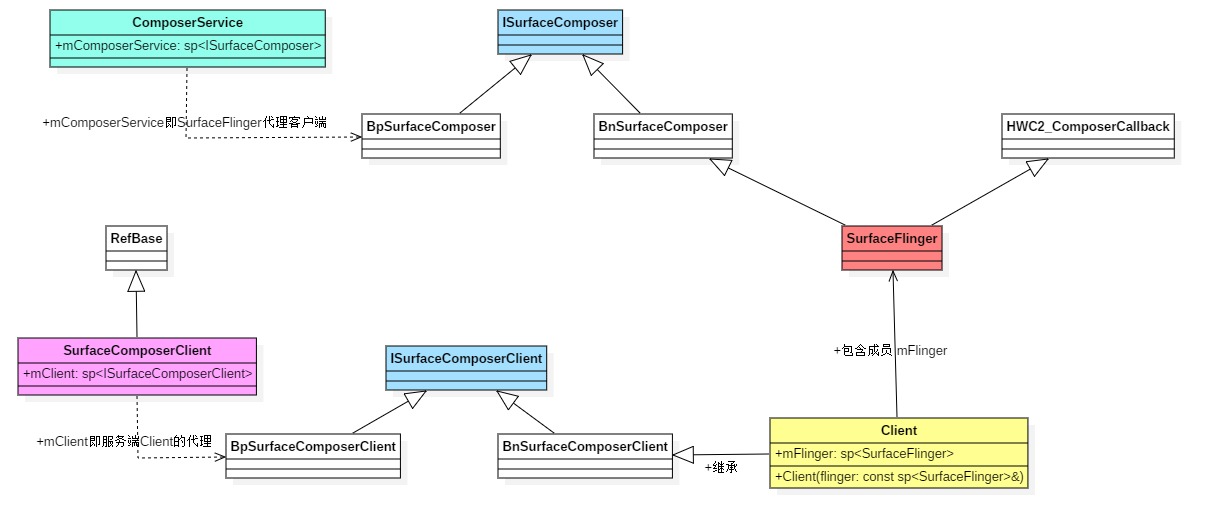
【安卓源码】SurfaceFlinger 启动及其与应用通信
1. surfaceFlinger 初始化和消息队列处理机制 surfaceflinger 的makefile 文件 /frameworks/native/services/surfaceflinger/Android.bp 235 cc_binary { 236 name: "surfaceflinger", 237 defaults: ["libsurfaceflinger_binary"], 238 i…...
springboot车辆充电桩
sprinboot车辆充电桩演示录像2022开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:ecli…...

linux进程和进程通信编程(1)
What makes the desert beautiful is that somewhere it hides a well. 沙漠之所以美丽,是因为在它的某个角落隐藏着一口井. linux进程和进程通信编程(1)1.什么是进程2.进程id(pid)3.进程间通信的方法管道信号IPCSocket4.创建进程forkfork有三个返回值父…...

操作系统(1.3)--习题
一、课堂习题 1、一个作业第一 次执行时用了5min ,而第二次执行时用了6min,这说明了操作系统的( )特点。 A、并发性 B、共享性 C、虚拟性 D、不确定性 D 2、在计算机系统中,操作系统是( )。 A、处于裸机之上的第一层软件 B、处于硬件之下的低层软件 C、处于应用软件之上的系统软…...

刷题笔记之十三(有假币、最难的问题、因子个数)
目录 1. 求正数数组的最小不可组成和 2. 有假币 3. 继承时先调用父类的构造方法;类中的成员变量的初始化操作都在构造方法时进行 4. 学会并理解装箱拆箱,注意new出来的也可以拆!! 5. getDeclaredMethods()是标识类或接口的声明成员(这个表示public private 包访问权限 pro…...
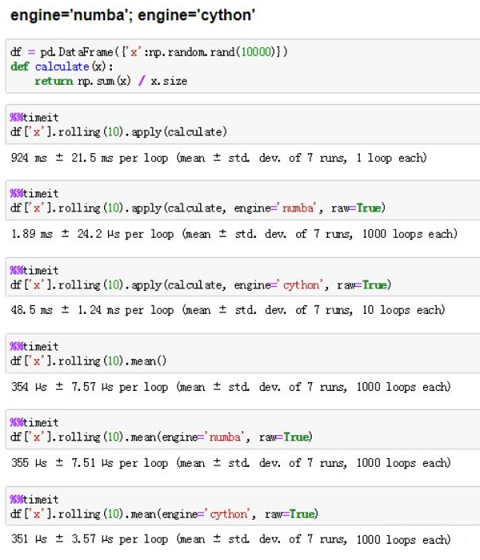
5个代码技巧,加速你的Python
5个代码技巧,加速你的Python 人生苦短,快学Python! Python作为一种功能强大的编程语言,因其简单易学而受到很多初学者的青睐。它的应用领域又非常广泛:科学计算、游戏开发、爬虫、人工智能、自动化办公、Web应用开发…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
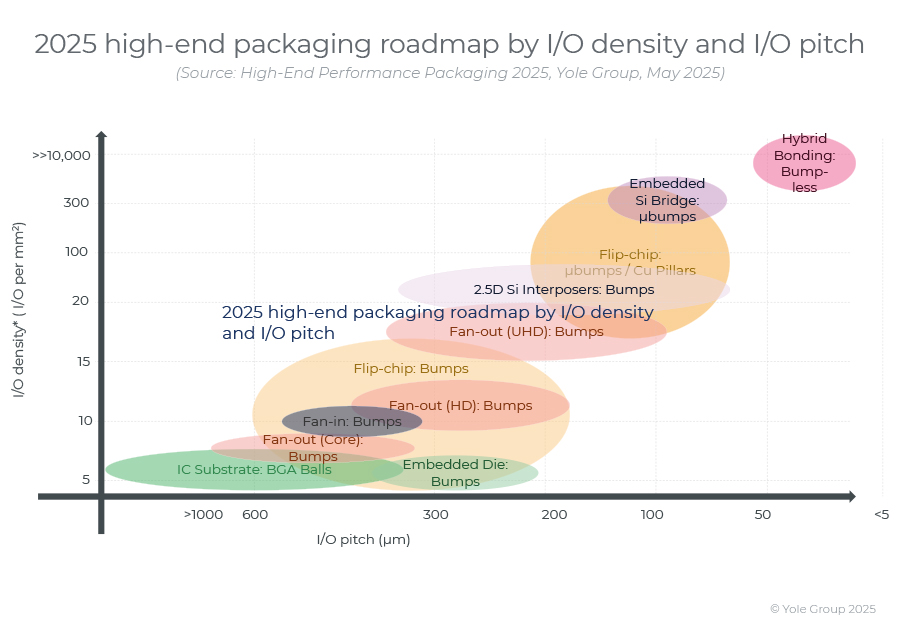
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
