java-数据结构与算法-02-数据结构-07-优先队列
1. 概念
队列是一种先进先出的结构,但是有些时候,要操作的数据带有优先级,一般出队时,优先级较高的元素先出队,这种数据结构就叫做优先级队列。
比如:你在打音游的时候,你的朋友给你打了个电话,这种时候,就应该优先处理电话,然后再来继续打音游,此时,电话就是优先级较高的。
在这种情况下,数据结构应该提供两个最基本的操作,一个是返回优先级最高的对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
2. 无序数组实现
要点
- 入队保持顺序
- 出队前找到优先级最高的出队,相当于一次选择排序
队列实现类:
package com.itheima.datastructure.priorityqueue;import com.itheima.datastructure.queue.Queue;/*** 优先队列实现类,基于无序数组。* 使用无序数组实现优先队列,队列中的元素必须实现Priority接口,以提供优先级比较的方法。* 该实现类提供了标准的队列操作,包括入队、出队、查看队首元素、判断队列为空或满等。** @param <E> 队列元素类型,必须实现Priority接口。*/
@SuppressWarnings("all")
public class PriorityQueue1<E extends Priority> implements Queue<E> {// 存储队列元素的数组,元素类型为Priority接口的实现类。Priority[] array;// 当前队列的大小。int size;/*** 构造函数,初始化优先队列。* * @param capacity 队列的容量,即最大元素数量。*/public PriorityQueue1(int capacity) {array = new Priority[capacity];}/*** 入队操作,将元素添加到队列尾部。* * @param e 待添加到队列的元素,必须实现Priority接口。* @return 添加成功返回true,队列已满返回false。*/@Override // O(1)public boolean offer(E e) {if (isFull()) {return false;}array[size++] = e;return true;}/*** 查找优先级最高的元素的索引。* * @return 优先级最高的元素的索引。*/// 返回优先级最高的索引值private int selectMax() {int max = 0;for (int i = 1; i < size; i++) {if (array[i].priority() > array[max].priority()) {max = i;}}return max;}/*** 出队操作,移除并返回优先级最高的元素。* * @return 被移除的优先级最高的元素,队列为空时返回null。*/@Override // O(n)public E poll() {if (isEmpty()) {return null;}int max = selectMax();E e = (E) array[max];remove(max);return e;}/*** 从数组中移除指定索引的元素,并将后续元素向前移动一位。* * @param index 待移除元素的索引。*/private void remove(int index) {if (index < size - 1) {// 移动System.arraycopy(array, index + 1,array, index, size - 1 - index);}array[--size] = null; // help GC}/*** 查看队首元素,即优先级最高的元素,但不移除。* * @return 队首元素,队列为空时返回null。*/@Overridepublic E peek() {if (isEmpty()) {return null;}int max = selectMax();return (E) array[max];}/*** 判断队列是否为空。* * @return 队列为空返回true,否则返回false。*/@Overridepublic boolean isEmpty() {return size == 0;}/*** 判断队列是否已满。* * @return 队列已满返回true,否则返回false。*/@Overridepublic boolean isFull() {return size == array.length;}
}
优先级类:
package com.itheima.datastructure.priorityqueue;public interface Priority {/*** 返回对象的优先级, 约定数字越大, 优先级越高* @return 优先级*/int priority();
}
条目类:
/*** 优先队列中的条目类,实现了Priority接口。* 该类用于存储具有特定优先级的值。*/
package com.itheima.datastructure.priorityqueue;class Entry implements Priority {String value; // 条目的值int priority; // 条目的优先级/*** 构造函数,创建一个具有指定优先级的条目。* @param priority 条目的优先级*/public Entry(int priority) {this.priority = priority;}/*** 构造函数,创建一个具有指定值和优先级的条目。* @param value 条目的值* @param priority 条目的优先级*/public Entry(String value, int priority) {this.value = value;this.priority = priority;}/*** 返回条目的优先级。* @return 条目的优先级*/@Overridepublic int priority() {return priority;}/*** 返回表示条目的字符串,格式为"(值 priority=优先级)"。* @return 表示条目的字符串*/@Overridepublic String toString() {return "(" + value + " priority=" + priority + ")";}/*** 比较当前对象与另一个对象是否相等。* 两个条目相等的定义是它们的优先级相同。* @param o 要比较的对象* @return 如果两个对象的优先级相同,则返回true;否则返回false。*/@Overridepublic boolean equals(Object o) {if (this == o) return true;if (o == null || getClass() != o.getClass()) return false;Entry entry = (Entry) o;return priority == entry.priority;}/*** 计算当前对象的哈希码,基于条目的优先级。* @return 当前对象的哈希码*/@Overridepublic int hashCode() {return priority;}
}测试类:
package com.itheima.datastructure.priorityqueue;import org.junit.jupiter.api.Test;import java.util.Arrays;import static org.junit.jupiter.api.Assertions.assertEquals;
import static org.junit.jupiter.api.Assertions.assertFalse;/*优先级队列 一端进, 另一端出 按优先级出队普通队列 一端进, 另一端出 FIFO
*/
public class TestPriorityQueue1 {@Testpublic void poll() {PriorityQueue1<Entry> queue = new PriorityQueue1<>(5);queue.offer(new Entry("task1", 4));queue.offer(new Entry("task2", 3));queue.offer(new Entry("task3", 2));queue.offer(new Entry("task4", 5));queue.offer(new Entry("task5", 1));assertFalse(queue.offer(new Entry("task6", 7)));System.out.println(Arrays.toString(queue.array));assertEquals(5, queue.poll().priority());System.out.println(Arrays.toString(queue.array));assertEquals(4, queue.poll().priority());assertEquals(3, queue.poll().priority());assertEquals(2, queue.poll().priority());assertEquals(1, queue.poll().priority());}
}测试结果:
[(task1 priority=4), (task2 priority=3), (task3 priority=2), (task4 priority=5), (task5 priority=1)]
[(task1 priority=4), (task2 priority=3), (task3 priority=2), (task5 priority=1), null]
3. 有序数组实现
要点
- 入队后排好序,优先级最高的排列在尾部
- 出队只需删除尾部元素即可
队列实现类:
package com.itheima.datastructure.priorityqueue;import com.itheima.datastructure.queue.Queue;/*** 基于有序数组实现的优先队列。* 使用优先级高的元素先出(FIFO)的策略。** @param <E> 队列中元素的类型,必须实现Priority接口以定义优先级。*/
@SuppressWarnings("all")
public class PriorityQueue2<E extends Priority> implements Queue<E> {// 存储元素的数组,数组中的元素必须实现Priority接口Priority[] array;// 当前队列中元素的数量int size;/*** 构造函数,初始化优先队列。** @param capacity 队列的容量,即最大元素数量。*/public PriorityQueue2(int capacity) {array = new Priority[capacity];}/*** 向队列中添加一个元素。* 如果队列已满,则返回false。** @param e 要添加到队列的元素,必须实现Priority接口。* @return 如果添加成功,返回true;否则返回false。*/@Overridepublic boolean offer(E e) {if (isFull()) {return false;}insert(e);size++;return true;}/*** 将元素插入到队列的正确位置,以保持队列的有序性。** @param e 要插入的元素。*/// O(n)private void insert(E e) {int i = size - 1;while (i >= 0 && array[i].priority() > e.priority()) {array[i + 1] = array[i];i--;}array[i + 1] = e;}/*** 从队列中移除并返回优先级最高的元素。* 如果队列为空,则返回null。** @return 被移除的元素,如果队列为空,则返回null。*/// O(1)@Overridepublic E poll() {if (isEmpty()) {return null;}E e = (E) array[size - 1];array[--size] = null; // help GCreturn e;}/*** 返回优先级最高的元素,但不移除它。* 如果队列为空,则返回null。** @return 队列头部的元素,如果队列为空,则返回null。*/@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[size - 1];}/*** 检查队列是否为空。** @return 如果队列为空,返回true;否则返回false。*/@Overridepublic boolean isEmpty() {return size == 0;}/*** 检查队列是否已满。** @return 如果队列已满,返回true;否则返回false。*/@Overridepublic boolean isFull() {return size == array.length;}
}测试类:
package com.itheima.datastructure.priorityqueue;import org.junit.jupiter.api.Test;import static org.junit.jupiter.api.Assertions.assertEquals;
import static org.junit.jupiter.api.Assertions.assertFalse;public class TestPriorityQueue2 {@Testpublic void poll() {PriorityQueue2<Entry> queue = new PriorityQueue2<>(5);queue.offer(new Entry("task1", 4));queue.offer(new Entry("task2", 3));queue.offer(new Entry("task3", 2));queue.offer(new Entry("task4", 5));queue.offer(new Entry("task5", 1));assertFalse(queue.offer(new Entry("task6", 7)));assertEquals("task4", queue.peek().value);assertEquals("task4", queue.poll().value);assertEquals("task1", queue.poll().value);assertEquals("task2", queue.poll().value);assertEquals("task3", queue.poll().value);assertEquals("task5", queue.poll().value);}
}4. 堆实现
JDK1.8中的 PriorityQueue 底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。也就是说,堆的是由完全二叉树调整而来的,可以存储到数组中。
堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或 大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值。
- 堆总是一棵完全二叉树。
如图:


计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。堆的特性如下
- 在大顶堆中,任意节点 C 与它的父节点 P 符合 P . v a l u e ≥ C . v a l u e P.value \geq C.value P.value≥C.value
- 而小顶堆中,任意节点 C 与它的父节点 P 符合 P . v a l u e ≤ C . v a l u e P.value \leq C.value P.value≤C.value
- 最顶层的节点(没有父亲)称之为 root 根节点
完全二叉树可以使用数组来表示

特征
● 如果从索引 0 开始存储节点数据
○ 节点 i i i 的父节点为 f l o o r ( ( i − 1 ) / 2 ) floor((i-1)/2) floor((i−1)/2),当 i > 0 i>0 i>0 时
○ 节点 i i i 的左子节点为 2 i + 1 2i+1 2i+1,右子节点为 2 i + 2 2i+2 2i+2,当然它们得 < s i z e < size <size
● 如果从索引 1 开始存储节点数据
○ 节点 i i i 的父节点为 f l o o r ( i / 2 ) floor(i/2) floor(i/2),当 i > 1 i > 1 i>1 时
○ 节点 i i i 的左子节点为 2 i 2i 2i,右子节点为 2 i + 1 2i+1 2i+1,同样得 < s i z e < size <size
实现类:
package com.itheima.datastructure.priorityqueue;import com.itheima.datastructure.queue.Queue;/*** 基于大顶堆实现的优先队列。* 大顶堆是一个完全二叉树,每个父节点的优先级不小于其子节点的优先级。* @param <E> 队列中元素的类型,必须实现Priority接口以定义元素的优先级。*/
@SuppressWarnings("all")
public class PriorityQueue4<E extends Priority> implements Queue<E> {Priority[] array; // 存储优先队列元素的数组int size; // 当前队列的大小/*** 构造函数,初始化优先队列。* @param capacity 队列的初始容量。*/public PriorityQueue4(int capacity) {array = new Priority[capacity];}/*** 向队列中添加一个元素。* 如果队列已满,则返回false;否则将元素加入队列,并调整堆以保持大顶堆的性质。* @param offered 要添加到队列的元素。* @return 如果添加成功,返回true;如果队列已满,返回false。*//*1. 入堆新元素, 加入到数组末尾 (索引位置 child)2. 不断比较新加元素与它父节点(parent)优先级 (上浮)- 如果父节点优先级低, 则向下移动, 并找到下一个 parent- 直至父节点优先级更高或 child==0 为止*/@Overridepublic boolean offer(E offered) {// 检查队列是否已满,如果已满,则拒绝添加新元素并返回false。if (isFull()) {return false;}// 将新元素插入到数组的末尾,并记录其位置。int child = size++;// 计算新元素的父节点位置。int parent = (child - 1) / 2;// 上浮新元素,直到它位于正确的位置或者它是根元素。while (child > 0 && offered.priority() > array[parent].priority()) {// 将当前元素的父元素移动到当前元素的位置,准备继续上浮。array[child] = array[parent];child = parent;// 更新当前元素的父节点位置。parent = (child - 1) / 2;}// 将新元素放置在最终的位置上,完成添加。array[child] = offered;// 添加成功,返回true。return true;}/*** 从队列中移除并返回优先级最高的元素(即堆顶元素)。* 如果队列为空,则返回null。* @return 优先级最高的元素,如果队列为空,则返回null。*//*1. 交换堆顶和尾部元素, 让尾部元素出队2. (下潜)- 从堆顶开始, 将父元素与两个孩子较大者交换- 直到父元素大于两个孩子, 或没有孩子为止*/@Overridepublic E poll() {// 检查队列是否为空,如果为空则返回nullif (isEmpty()) {return null;}// 交换堆顶元素(优先级最高)和队列尾部元素,准备移除堆顶元素swap(0, size - 1);// 更新队列大小,表示已移除一个元素size--;// 获取并保存即将返回的堆顶元素Priority e = array[size];// 将队列尾部元素置为null,帮助垃圾回收array[size] = null; // help GC// 调整堆结构,确保堆的性质依然满足// 下潜down(0);// 返回移除的堆顶元素return (E) e;}/*** 将元素向下调整以保持大顶堆的性质。* 此方法假设调用时堆已经部分有序,它通过比较父节点和其子节点的优先级来确保整个堆仍然满足大顶堆的定义。* 如果父节点的优先级低于某个子节点,则交换它们,并继续向下调整子节点,直到整个子树满足大顶堆的条件。** @param parent 需要向下调整的父节点的索引。*//*** 将元素向下调整以保持大顶堆的性质。* @param parent 需要向下调整的元素的索引。*/private void down(int parent) {// 计算左子节点和右子节点的索引int left = 2 * parent + 1;int right = left + 1;// 假设当前父节点的优先级最高int max = parent; // 假设父元素优先级最高// 如果左子节点存在且优先级高于当前最大值,则更新最大值索引if (left < size && array[left].priority() > array[max].priority()) {max = left;}// 如果右子节点存在且优先级高于当前最大值,则更新最大值索引if (right < size && array[right].priority() > array[max].priority()) {max = right;}// 如果最大值不是初始的父节点,则交换它们,并递归向下调整新父节点if (max != parent) { // 有孩子比父亲大swap(max, parent);down(max);}}/*** 交换数组中两个元素的位置。* @param i 第一个元素的索引。* @param j 第二个元素的索引。*/private void swap(int i, int j) {Priority t = array[i];array[i] = array[j];array[j] = t;}/*** 返回队列中优先级最高的元素(即堆顶元素),但不移除它。* 如果队列为空,则返回null。* @return 优先级最高的元素,如果队列为空,则返回null。*/@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[0];}/*** 检查队列是否为空。* @return 如果队列为空,返回true;否则返回false。*/@Overridepublic boolean isEmpty() {return size == 0;}/*** 检查队列是否已满。* @return 如果队列已满,返回true;否则返回false。*/@Overridepublic boolean isFull() {return size == array.length;}
}5. 习题
E01. 合并多个有序链表-Leetcode 23
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[1->4->5,1->3->4,2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:输入:lists = [[]]
输出:[]
提示:
k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10^4
这道题目之前解答过,现在用刚学的优先级队列来实现一下
题目中要从小到大排列,因此选择用小顶堆来实现,思路如下图:

自定义小顶堆如下
package com.itheima.datastructure.priorityqueue;import com.itheima.datastructure.linkedlist.ListNode;/*** 小顶堆类,实现优先队列功能。* 小顶堆是一个完全二叉树,每个父节点的值都小于或等于其子节点的值。*/
/*** <b>小顶堆</b>*/
public class MinHeap {/*** 堆数组,存储堆中的节点。*/ListNode[] array;/*** 堆的当前大小,即堆中节点的数量。*/int size;/*** 构造函数,初始化小顶堆。** @param capacity 堆的容量,即堆数组的大小。*/public MinHeap(int capacity) {array = new ListNode[capacity];}/*** 将一个节点添加到最小堆中。* 如果堆已满,则拒绝添加,并返回false;否则,将节点添加到堆中并维护堆的性质。** @param offered 要添加到堆中的节点。* @return 如果成功添加节点,则返回true;如果堆已满,则返回false。*//*** 向堆中插入一个节点。** @param offered 要插入的节点。* @return 如果堆已满,返回false;否则返回true。*/public boolean offer(ListNode offered) {// 检查堆是否已满,如果已满则无法添加新节点if (isFull()) {return false;}// 将新节点插入到堆的最后一个位置,并更新堆的大小int child = size++;// 计算新节点的父节点位置int parent = (child - 1) / 2;// 当节点不在根位置且小于其父节点时,向上调整节点位置以维护最小堆性质while (child > 0 && offered.val < array[parent].val) {// 将父节点值复制到当前节点array[child] = array[parent];// 更新当前节点为父节点,并计算新的父节点位置child = parent;parent = (child - 1) / 2;}// 将新节点值插入到最终位置,完成添加array[child] = offered;return true;}/*** 从堆中移除并返回最小的节点。** @return 如果堆为空,返回null;否则返回移除的最小节点。*/public ListNode poll() {if (isEmpty()) {return null;}swap(0, size - 1);size--;ListNode e = array[size];array[size] = null; // help GC// 下潜down(0);return e;}/*** 将堆中指定元素下沉以维护堆的性质。* 这个方法是堆排序或优先队列操作中的关键部分,它确保堆的性质得以维持。* 当插入一个新元素或某个元素的值被更新后,可能需要调用此方法来重新调整堆。** @param parent 要下沉的元素的索引,该元素是其子节点的父节点。*/private void down(int parent) {// 计算左子节点和右子节点的索引int left = 2 * parent + 1;int right = left + 1;// 假设当前父节点是最小的// 如果左子节点存在且值小于当前最小值,则更新最小值为左子节点int min = parent; // 假设父元素最小if (left < size && array[left].val < array[min].val) {min = left;}// 如果右子节点存在且值小于当前最小值,则更新最小值为右子节点if (right < size && array[right].val < array[min].val) {min = right;}// 如果找到的最小值不是初始的父节点,则交换它们并继续下沉最小值节点if (min != parent) { // 有孩子比父亲小swap(min, parent);down(min);}}/*** 交换堆数组中两个节点的位置。** @param i 第一个节点的索引。* @param j 第二个节点的索引。*/private void swap(int i, int j) {ListNode t = array[i];array[i] = array[j];array[j] = t;}/*** 检查堆是否为空。** @return 如果堆为空,返回true;否则返回false。*/public boolean isEmpty() {return size == 0;}/*** 检查堆是否已满。** @return 如果堆已满,返回true;否则返回false。*/public boolean isFull() {return size == array.length;}
}代码
package com.itheima.datastructure.priorityqueue;import com.itheima.datastructure.linkedlist.ListNode;/*** 合并多个有序链表的工具类。*/
public class E01Leetcode23 {/*** 使用最小堆合并多个有序链表。* * @param lists 多个有序链表的数组形式。* @return 合并后的单个有序链表。*/public ListNode mergeKLists2(ListNode[] lists) {MinHeap heap = new MinHeap(100);// 将所有链表的节点加入最小堆// 1. 将链表的所有节点加入小顶堆for (ListNode p : lists) {while (p != null) {heap.offer(p);p = p.next;}}// 从最小堆中依次取出节点构建合并后的链表// 2. 不断从堆顶移除最小元素, 加入新链表ListNode s = new ListNode(-1, null);ListNode t = s;while(!heap.isEmpty()) {ListNode min = heap.poll();t.next = min;t = min;t.next = null; // 保证尾部节点指向 null}return s.next;}/*** 使用最小堆合并多个有序链表的另一种实现方式。* * @param lists 多个有序链表的数组形式。* @return 合并后的单个有序链表。*/public ListNode mergeKLists(ListNode[] lists) {MinHeap heap = new MinHeap(lists.length);// 将所有链表的头节点加入最小堆// 1. 将链表的头节点加入小顶堆for (ListNode h : lists) {if(h != null) {heap.offer(h);}}// 从最小堆中依次取出节点构建合并后的链表// 2. 不断从堆顶移除最小元素, 加入新链表ListNode s = new ListNode(-1, null);ListNode t = s;while(!heap.isEmpty()) {ListNode min = heap.poll();t.next = min;t = min;// 将当前节点的下一个节点加入最小堆// 将最小元素的下一个节点加入到堆if(min.next != null) {heap.offer(min.next);}}return s.next;}/*** 测试合并多个有序链表的函数。* * @param args 命令行参数。*/public static void main(String[] args) {ListNode[] lists = {ListNode.of(1, 4, 5),ListNode.of(1, 3, 4),ListNode.of(2, 6),null,};ListNode m = new E01Leetcode23().mergeKLists2(lists);System.out.println(m);}
}相关文章:

java-数据结构与算法-02-数据结构-07-优先队列
1. 概念 队列是一种先进先出的结构,但是有些时候,要操作的数据带有优先级,一般出队时,优先级较高的元素先出队,这种数据结构就叫做优先级队列。 比如:你在打音游的时候,你的朋友给你打了个电话…...

从0开始搭建vue + flask 旅游景点数据分析系统(一):创建前端项目
基于scrapy爬取到的景点和评论数据,本期开始搭建一个vueflask的前后端分离的数据分析系统。 本教程为麦麦原创,也可以去B站找我 👉🏻 我的空间 🧑🎓 前置课程 🕸 scrapy实战 爬取景点信息和…...

支持AI的好用的编辑器aieditor
一、工具概述 AiEditor 是一个面向 AI 的下一代富文本编辑器,她基于 Web Component,因此支持 Layui、Vue、React、Angular 等几乎任何前端框架。她适配了 PC Web 端和手机端,并提供了 亮色 和 暗色 两个主题。除此之外,她还提供了…...

数据结构之《栈》
在之前我们已经学习了数据结构中线性表里面的顺序表与链表,了解了如何实现顺序表与链表增、删、查、该等功能。其实在线性表中除了顺序表和链表还有其他的类别,在本篇中我们就将学习另外一种线性表——栈,在通过本篇的学习后,你将…...

Vue3基础语法
一:创建Vue3工程(适用Vite打包工具) Vite官网:Home | Vite中文网 (vitejs.cn) 直接新建一个文件夹,打开cmd运行: npm create vitelatest 选择Vue和TS语言即可 生成一个项目。 Vue3的核心语法ÿ…...

【Python】基础学习技能提升代码样例4:常见配置文件和数据文件读写ini、yaml、csv、excel、xml、json
一、 配置文件 1.1 ini 官方-configparser config.ini文件如下: [url] ; section名称baidu https://www.zalou.cnport 80[email]sender ‘xxxqq.com’import configparser # 读取 file config.ini # 创建配置文件对象 con configparser.ConfigParser() # 读…...

JavaScript基础——JavaScript调用的三种方式
JavaScript简介 JavaScript的作用 JavaScript的使用方式 内嵌JS 引入外部js文件 编写函数 JavaScript简介 JavaScript(简称“JS”)是一种具有函数优先的轻量级,解释型或即时编译型的编程语言。它是Web开发中最常用的脚本语言之一&#x…...

ITSS:IT服务工程师
证书亮点:适中的费用、较低的难度、广泛的应用范围以及专业的运维认证。 总体评价:性价比良好! 证书名称:ITSS服务工程师 证书有效期:持续3年 培训要求:必须参加培训,否则将无法参与考试 发…...

鸿蒙开发——axios封装请求、拦截器
描述:接口用的是PHP,框架TP5 源码地址 链接:https://pan.quark.cn/s/a610610ca406 提取码:rbYX 请求登录 HttpUtil HttpApi 使用方法...

Scikit-Learn中的分层特征工程:构建更精准的数据洞察
Scikit-Learn中的分层特征工程:构建更精准的数据洞察 在机器学习中,特征工程是提升模型性能的核心技术之一。Scikit-Learn(简称sklearn),作为Python中广受欢迎的机器学习库,提供了多种方法来进行特征工程&…...

CSOL遭遇DDOS攻击如何解决
CSOL遭遇DDOS攻击如何解决?在错综复杂的数字网络丛林中,《Counter-Strike Online》(简称CSOL)犹如一座坚固的堡垒,屹立在游戏世界的中心,吸引着无数玩家的目光与热情。这座堡垒并非无懈可击,DDo…...
基于python的BP神经网络红酒品质分类预测模型
1 导入必要的库 import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.preprocessing import LabelEncoder from tensorflow.keras.models import Sequential from tenso…...

Kylin与Spark:大数据技术集成的深度解析
引言 在大数据时代,企业面临着海量数据的处理和分析需求。Kylin 和 Spark 作为两个重要的大数据技术,各自在数据处理领域有着独特的优势。Kylin 是一个开源的分布式分析引擎,专为大规模数据集的 OLAP(在线分析处理)查…...

⌈ 传知代码 ⌋ 利用scrapy框架练习爬虫
💛前情提要💛 本文是传知代码平台中的相关前沿知识与技术的分享~ 接下来我们即将进入一个全新的空间,对技术有一个全新的视角~ 本文所涉及所有资源均在传知代码平台可获取 以下的内容一定会让你对AI 赋能时代有一个颠覆性的认识哦&#x…...
)
深入了解 Python 面向对象编程(最终篇)
大家好!今天我们将继续探讨 Python 中的类及其在面向对象编程(OOP)中的应用。面向对象编程是一种编程范式,它使用“对象”来模拟现实世界的事务,使代码更加结构化和易于维护。在上一篇文章中,我们详细了解了…...

手把手教你实现基于丹摩智算的YoloV8自定义数据集的训练、测试。
摘要 DAMODEL(丹摩智算)是专为AI打造的智算云,致力于提供丰富的算力资源与基础设施助力AI应用的开发、训练、部署。 官网链接:https://damodel.com/register?source6B008AA9 平台的优势 💡 超友好! …...

SSH相关
前言 这篇是K8S及Rancher部署的前置知识。因为项目部署测试需要,向公司申请了一个虚拟机做服务器用。此前从未接触过服务器相关的东西,甚至命令也没怎么接触过(接触最多的还是git命令,但我日常用sourceTree)。本篇SSH…...
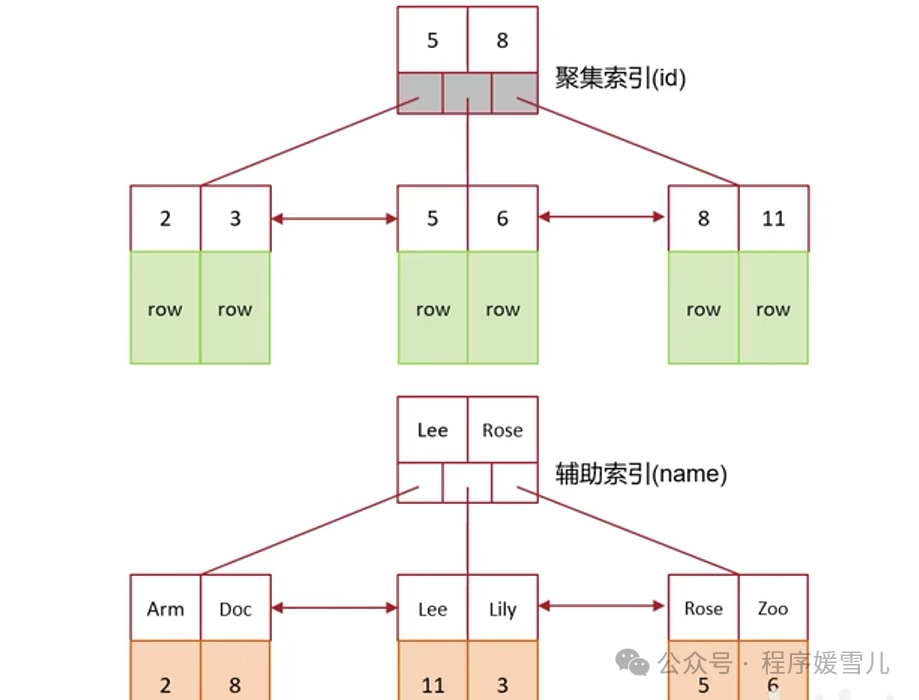
mysql超大分页问题处理~
大家好,我是程序媛雪儿,今天咱们聊mysql超大分页问题处理。 超大分页问题是什么? 数据量很大的时候,在查询中,越靠后,分页查询效率越低 例如 select * from tb_sku limit 0,10; select * from tb_sku lim…...

Gitlab以及分支管理
一、概述 Git 是一个分布式版本控制系统,用于跟踪文件的变化,尤其是源代码的变化。它由 Linus Torvalds 于 2005 年开发,旨在帮助管理大型软件项目的开发过程。 二、Git 的功能特性 Git 是关注于文件数据整体的变化,直接会将文件…...

探索Axure在数据可视化原型设计中的无限可能
在当今数字化浪潮中,产品设计不仅关乎美观与功能的平衡,更在于如何高效、直观地传达复杂的数据信息。Axure RP,作为原型设计领域的佼佼者,其在数据可视化原型设计中的应用,正逐步揭开产品设计的新篇章。本文将从多个维…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
