我常用的shell 进制转换工具
一、进制的一些基础知识
1. 二进制(binary)
二进制的取值是0和1; 前缀是 0b
2. 八进制(Octal)
八进制的取值是0-7;前缀是 O
3. 十进制(decimal)
十进制的取值是0-9;没有前缀
4. 十六进制(hexadecimal)
十六进制的取值是 0-9,A-F;前缀是 0x
二、常用转换函数
1. bc 命令
An arbitrary precision calculator language . 任意精度的计数器语言
使用格式如下:
echo "obase = 2 ; ibase = 10 ; 9 "|bc
- obase : 指定输出进制
- ibase : 指定输入进制
- 参数之间通过
;分割 - 最后一个参数是要转换的数据
- 对于要转换的数据,不需要写前缀(
0b,O,0x)。当它是十六进制数时,‘A-F’部分要写大写。
2. printf 命令
format and print data
使用格式如下:
printf '%d\n' 0b1001
使用printf 时,有部分进制之间不能转换,暂时不清楚原因。
3. echo 实现任意进制转十进制
-
十六进制转十进制
echo $((16#F)) //输出15 -
八进制转十进制
echo $((8#15)) //输出13 -
二进制转十进制
echo $((2#1001)) //输出9
从上面转换可以看出,# 号前面表示当前数据的进制,后面表示要转换的数据,要转换的数据不需要带前缀。
三、常见的转换
1. 二进制、十进制互转
二进制转十进制
printf '%d\n' 0b1001
执行后输出:9
十进制转二进制
echo "obase = 2 ; ibase = 10 ; 9 "|bc
执行后输出:1001
2. 十进制 、十六进制互转
十进制转十六进制
printf "%x\n" 15
执行后输出:f
十六进制转十进制
printf "%d\n" 0x0f
执行后输出:15
3. 十进制 、八进制互转
十进制转八进制
printf "%o\n" 15
执行后输出:17 (八进制)
八进制转十进制
echo "obase=10;ibase=8; 15"|bc
执行后输出:13
相关文章:

我常用的shell 进制转换工具
一、进制的一些基础知识 1. 二进制(binary) 二进制的取值是0和1; 前缀是 0b 2. 八进制(Octal) 八进制的取值是0-7;前缀是 O 3. 十进制(decimal) 十进制的取值是0-9;没有前缀 …...
手写vue(二)响应式实现
名词解释:vm:指Vue实例一、目标效果vue定义(1)新建vm时,可以通过一个data对象,或者data函数,其属性可以通过vm直接访问,而data对象可以通过vm._data获取(2)修…...

mysql数据库常问面试题
1、NOW()和CURRENT_DATE()有什么区别? NOW()命令用于显示当前年份,月份,日期,小时,分钟和秒。 CURRENT_DATE()仅显示当前年份,月份和日期。 2、CHAR和VARCHAR的区别? (1)…...

AI风暴 :文心一言 VS GPT-4
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! 文心一言 VS GPT-4 文心一言:知识增强大语言模型百度全新一代知识增强大语言模型,文心大模型家族的新成员,能够与人对话互动&#…...
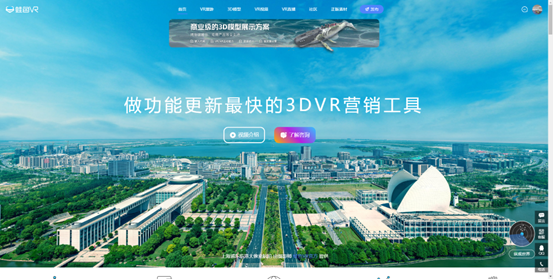
VR全景城市,用720全景树立城市形象,打造3D可视化智慧城市
随着城市化进程的加速,城市之间的竞争也日益激烈。城市管理者们需要寻求新的方式来提升城市的品牌形象和吸引力。在这个过程中,VR全景营销为城市提供了一种全新的营销手段,可以帮助提升城市的价值和吸引力。一、城市宣传新方式VR全景营销是一…...
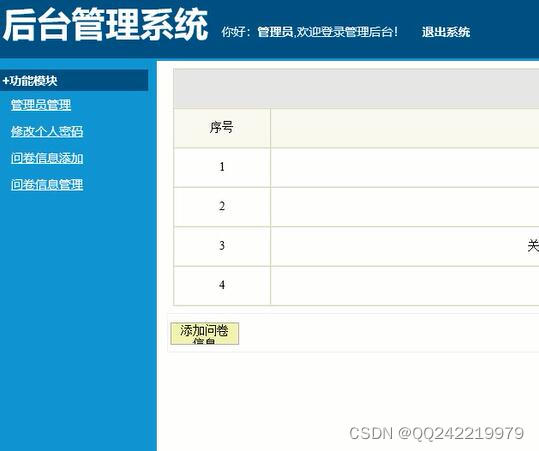
javaweb窗口服务人员分析评价系统ssh
A)后台管理员模块:通过该功能模块,管理员可以修改自己的密码,并对管理员进行添加和删除操作。 B)注册用户模块:通过该功能模块,管理员可以查看注册用户的基本信息,对存在问题的用户进…...
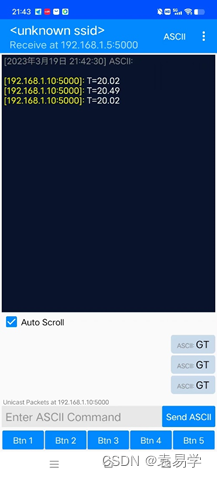
树莓派Pico W无线开发板UDP协议MicroPython网络编程实践
树莓派Pico W无线开发板(简称Pico W)是树莓派基金会于2022年6月底推出的搭载无线通信芯片的树莓派Pico开发板。本文在介绍树莓派Pico W无线开发板接口信号和TCP/IP和UDP通信协议基础上,给出Pico W无线开发板的UDP协议MicroPython网络编程实例…...
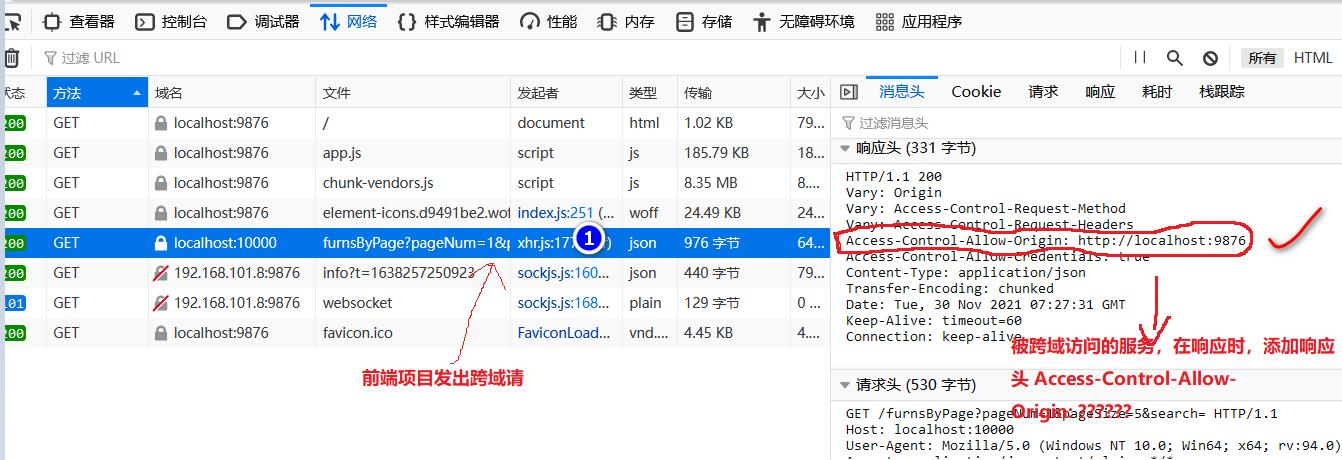
跨域解决方案
跨域解决方案 1.跨域基本介绍 文档:https://developer.mozilla.org/zh-CN/docs/Web/HTTP/CORS 跨域问题是什么? 一句话:跨域指的是浏览器不能执行其他网站的脚本,它是由浏览器的同源策略造成的,是浏览器对 javascr…...

springboot的统一处理
在处理网络请求时,有一部分功能是需要抽出来统一处理的,与业务隔开。 登录校验 可以利用spring mvc的拦截器Interceptor,实现HandlerInterceptor接口即可。实现该接口后,会在把请求发给Controller之前进行拦截处理。 拦截器的实…...

C/C++每日一练(20230319)
目录 1. 反转链表 II 🌟🌟 2. 解码方法 🌟🌟 3. 擅长编码的小k 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 …...

GitHub 上有些什么好玩的项目?
前言 各个领域模块的都整理了一下,包含游戏、一些沙雕的工具、实用正经的工具以及一些相关的电商项目,希望他们可以给你学习的路上增加几分的乐趣,我们直接进入正题~ 游戏 1.吃豆人 一款经典的游戏开发案例,包括地图绘制、玩家控…...

蓝桥杯刷题第十二天
问题描述给定一个正整数 n ,请问 n 的十进制表示中末尾总共有几个 0 ?输入格式输入一行包含一个正整数 n。输出格式输出一个整数,表示答案。评测用例规模与约定对于所有评测用例,1 < n < 1000000000。运行限制最大运行时间&…...
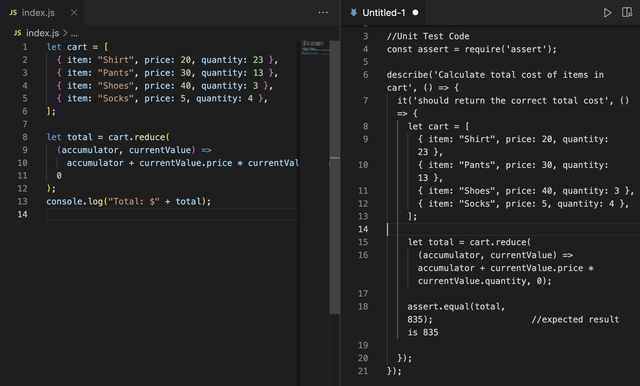
开发也可以很快乐,让VSCode和CodeGPT带给你幸福感
CodeGPT 是一款 Visual Studio Code 扩展,可以通过官方的 OpenAI API 使用 GPT-3 (预训练生成式转换器) 模型,在多种编程语言中生成、解释、重构和文档化代码片段。CodeGPT 可用于各种任务,例如代码自动完成、生成和格式化。它还可以集成到代…...
【Linux】基本指令介绍
前言从今天开始,我们一起来学习Linux的相关知识,今天先来介绍怎么登录Linux,并且介绍一些Linux的基本指令。使用 XShell 远程登录 Linux很多同学的 Linux 启动进入图形化的桌面. 这个东西大家以后就可以忘记了. 以后的工作中 没有机会 使用图…...

JQuery介绍
文章目录一. JQuery介绍二. JQuery使用三. JQuery选择器四. JQuery选择集过滤五.JQuery选择集转移六. JQuery获取和操作标签内容七. JQuery获取和设置元素属性八. JQuery事件九.JQuery事件代理- 事件冒泡- 事件绑定的问题- 事件代理一. JQuery介绍 定义: jquery是JS的一个函数…...
Selenium基础篇之八大元素定位方式
文章目录前言一、如何进行元素定位?1.右击元素-检查2.F12-选择工具点击元素3.借助selenium IDE二、八大元素定位方式1.ID1.1 方法1.2 举例1.3 代码1.4 截图2.NAME2.1 方法2.2 举例2.3 代码2.4 截图3.CLASS_NAME3.1 方法3.2 举例3.3 代码3.4 截图4.TAG_NAME4.1 方法4…...

C语言的灵魂---指针(基础)
C语言灵魂指针1.什么是指针?2.指针的大小3.指针的分类3.1比较常规的指针类型3.2指针的解引用操作3.3野指针野指针的成因:4.指针运算4.1指针加减整数4.2指针-指针1.什么是指针? 这个问题我们通常解释为两种情况: 1.指针本质&#…...

带你一文透彻学习【PyTorch深度学习实践】分篇——线性模型 梯度下降
分享给大家一段我国著名作家、散文家史铁生先生的一段话: 把路想象的越是坎坷就越是害怕,把山想象的越是险峻就越会胆怯,把别人想象的越是优秀就越是不敢去接近。惯于这样想象的人,是天生谦卑的人。 --------史铁生《关于恐惧》 🎯作者主页:追光者♂🔥 �…...

Javascript如何截取含有表情的字符串
Javascript如何截取含有表情的字符串 一、说说背景 社区社交应用中,难免会有输入用户昵称的操作,如果用户老老实实的输入中文汉字或者英文字母,那当然没啥问题,我们能够轻松的处理字符串的截取,产品说按多少字符截取…...
【云原生】prometheus结合jmx exporter 的java agent模式采集tomcat监控实战
前言 大家好,我是沐风晓月,今天我们又来探讨一款使用prometheus监控tomcat的另外一种形式:Java agent模式。 如果你想使用http server模式,请参考:【云原生】prometheus结合jmx exporter 的http server模式采集tomca…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
