分页和mmap
文章目录
- 一、内存分页
- 1、基本概念
- 2、分页机制下,虚拟地址和物理地址是如何映射的?
- 3、快表(TLB)
- 二、mmap基本原理和分类
一、内存分页
1、基本概念
CPU并不是直接访问物理内存地址,而是通过虚拟地址空间来间接的访问物理内存地址。
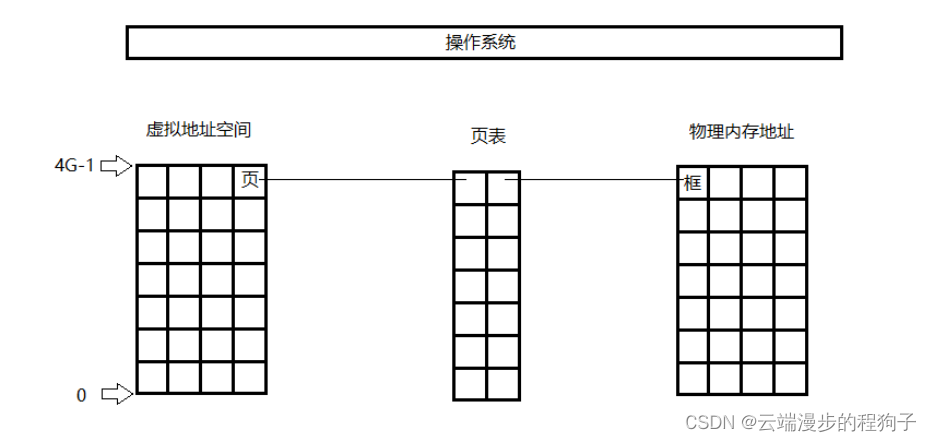
页:通常将虚拟地址空间以4K大小分成;
框:将物理地址按照同样的大小,作为一个单位;也从0开始依次对每一个框编号。
页表:操作系统通过维护一张表,这张表上记录了每一对页和框的映射关系。如图:
2、分页机制下,虚拟地址和物理地址是如何映射的?
在分页机制下,虚拟地址分为两部分,页号和页内偏移。页号作为页表的索引,页表包含物理页每页所在物理内存的基地址,这个基地址与页内偏移的组合就形成了物理内存地址,见下图。
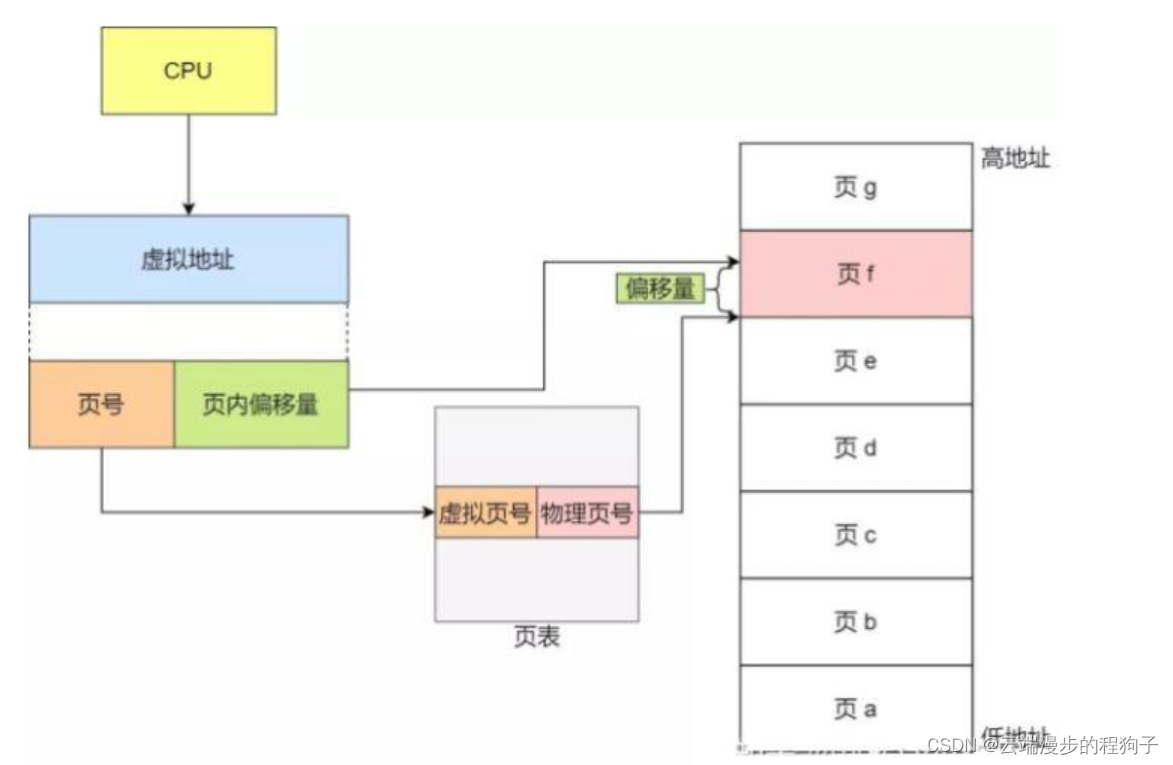
其实就是这样三个步骤:
把虚拟内存地址,切分成页号和偏移量;
根据页号,从页表里面,查询对应的物理页号;
直接拿物理页号,加上前面的偏移量,就得到了物理内存地址。
3、快表(TLB)
多级页表虽然解决了空间占用大的问题,但是由于其复杂化了地址的转换,因此也带来了大量的时间开销,使得地址转换速度减慢。
如果要解决这个问题,那么最简单的方式就是降低查询页表的频率,那么如何实现呢?这时候就需要用到缓存的技术
与我之前在Redis系列博客中所提到的,对于热点资源,我们可以将其提前缓存下来,到以后使用时就可以直接到缓存中查找。对于操作系统来说,也是这么一个道理。
在操作系统中,这个缓存就是CPU中的TLB,也就是我们通常所说的快表。我们将最常访问的几个页表项存储到TLB中,在之后进行寻址时,CPU就会先到TLB中进行查找,如果没有找到,这时才会去查询页表。
二、mmap基本原理和分类
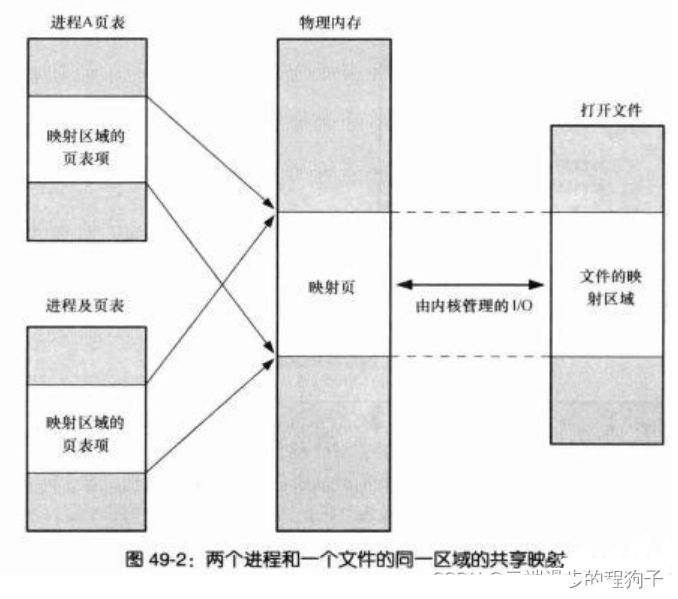
在LINUX中我们可以使用mmap用来在进程虚拟内存地址空间中分配地址空间,创建和物理内存的映射关系。
相关文章:

分页和mmap
文章目录一、内存分页1、基本概念2、分页机制下,虚拟地址和物理地址是如何映射的?3、快表(TLB)二、mmap基本原理和分类一、内存分页 1、基本概念 CPU并不是直接访问物理内存地址,而是通过虚拟地址空间来间接的访问物理内存地址。 页&#x…...
C++之异常处理
异常异常是面向对象语言处理错误的一种方式。当一个函数出现自己无法处理的错误时,可以抛出异常,然后输的直接或者间接调用者处理这个错误。语法捕获全部的异常try {//可能抛出异常的代码//throw异常对象 } catch(...) {//不管什么异常,都在这…...
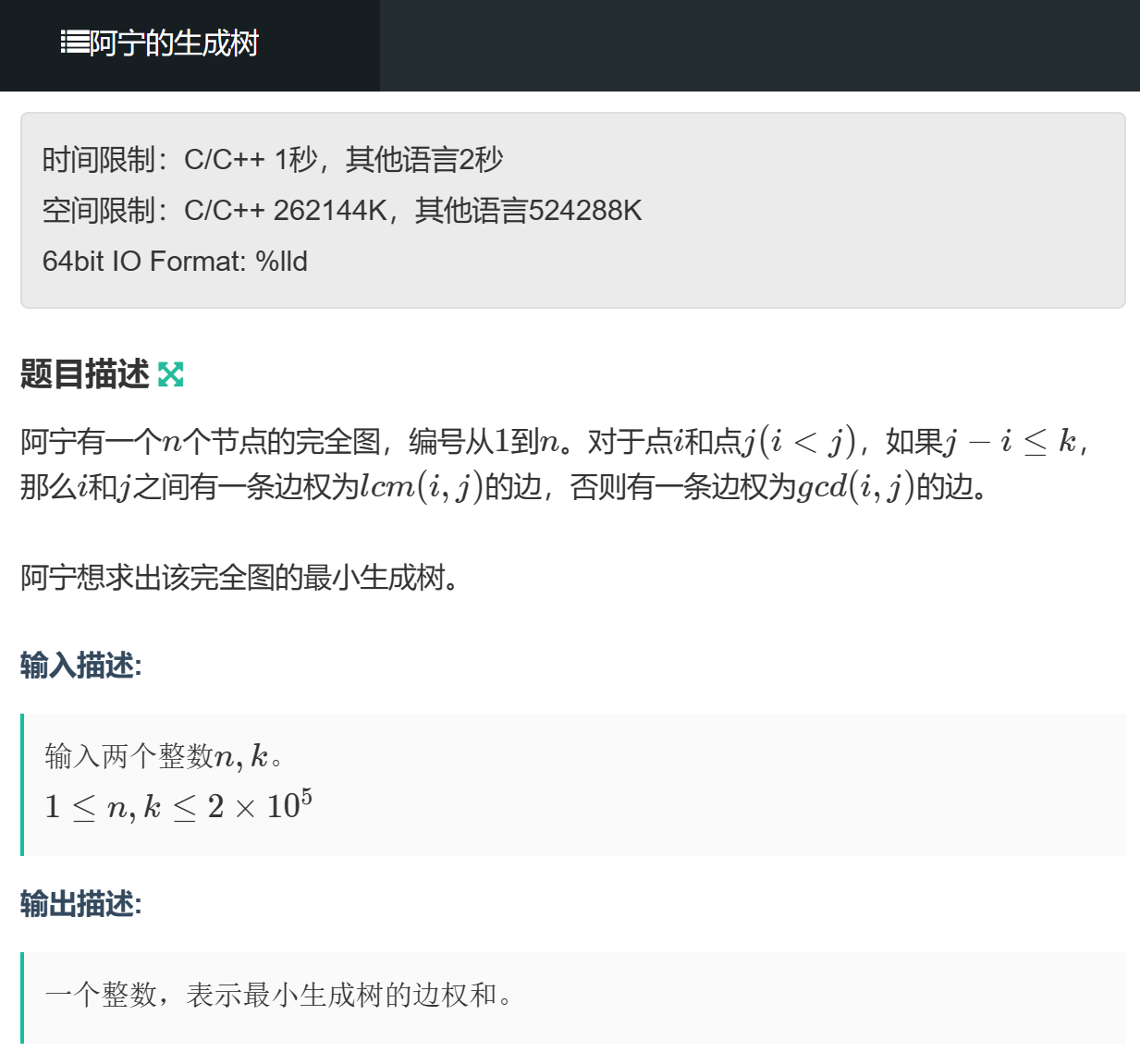
牛客寒假集训营6 E 阿宁的生成树
E-阿宁的生成树_2023牛客寒假算法基础集训营6 (nowcoder.com)开始慢慢补牛牛的题题意:最小生成树质数距离思路:最小生成树一共就两种算法,我们考虑Prim的过程初始连通块是1,然后考虑拿1和其他的结点连边当j-i<k时边权是gcd&…...
)
嵌入式C基础知识(10)
C语言如何实现一个频繁使用短小函数,C如何实现?C语言可以使用宏定义实现一个短小函数,如下面例子所示。但是宏定义语句不会进行检查,并且对书写格式有过分的讲究。比如MAX和括号之间不能有空格,每个参数都要放在括号里…...

TC3xx FlexRay™ 协议控制器 (E-Ray)-01
1 FlexRay™ 协议控制器 (E-Ray) E-Ray IP 模块根据为汽车应用开发的 FlexRay™ 协议规范 v2.1 执行通信【performs communication according to the FlexRay™ 1) protocol specification v2.1】。使用最大指定时钟,比特率可以编程为高达 10 Mbit/s 的值。连接到物…...

优劣解距离法TOPSIS——清风老师
TOPSIS法是一种常用的综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。 基本过程为先将原始数据矩阵统一指标类型(一般正向化处理)得到正向化的矩阵,再对正向化的矩阵进行标准化处理…...
【Unity3D】Shader常量、变量、结构体、函数
1 源码路径 Unity Shader 常量、变量、结构体、函数一般可以在 Unity Editor 安装目录下面的【Editor\Data\CGIncludes\UnityShader】目录下查看源码,主要源码文件如下: UnityCG.cgincUnityShaderUtilities.cgincUnityShaderVariables.cginc 2 Shader 常…...

LeetCode 刷题系列 -- 496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。对于每个 0 < i < nums1.length ,找出满…...
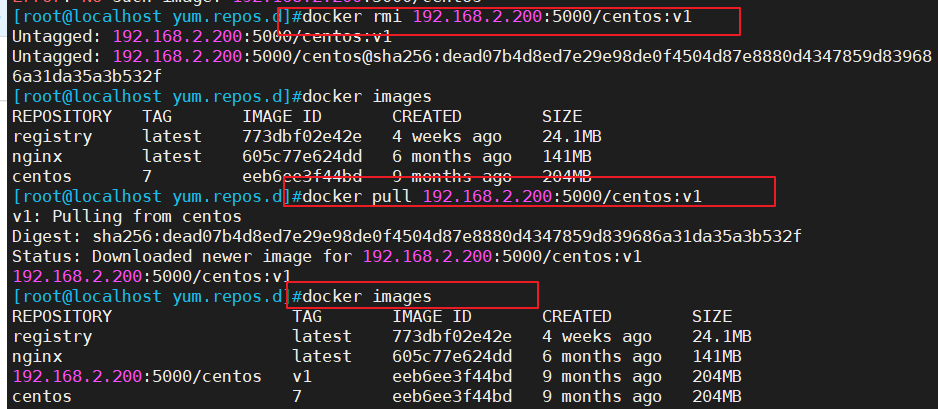
Docker 搭建本地私有仓库
一、搭建本地私有仓库有时候使用Docker Hub这样的公共仓库可能不方便,这种情况下用户可以使用registry创建一个本地仓库供私人使用,这点跟Maven的管理类似。使用私有仓库有许多优点:1)节省网络带宽,针对于每个镜像不用…...

XML中的CDATA且mybatis中特殊字符转义
如果想看如果CDATA在mybatis的xml文件中使用的可以直接跳转。 CDATA1 XML中的CDATA1.1 为什么叫CDATA1.2 CDATA在XML中的语法1.3 CDATA在XML中的例子1.4 CDATA规则2 Mybatis中的CDATA2.1 Mybatis中使用XML转义序列转义2.2 Mybatis中使用CDATA转义2.3 mybatis中使用CDATA需注意的…...

位运算 | 1356. 根据数字二进制下 1 的数目排序
LeetCode 1356. 根据数字二进制下 1 的数目排序 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中数字 1 的数目升序排序。如果存在多个数字二进制中 1 的数目相同,则必须将它们按照数值大小升序排列。 文章讲解https://www.programmercarl.com/1356.%…...

React Hooks之useState详解
1. 什么是Hooks? React官方简介:Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。 本文中讲解的useState就是React中的其中一个Hook。 2. useState useState 通过在函数组件里调用它来满足给组件添…...

选购交换机的参数依据和主要的参数指标详解
如何选购交换机?用什么交换机?在选购交换机时交换机的优劣无疑十分的重要,而交换机的优劣要从总体构架、性能和功能三方面入手。交换机选购时。性能方面除了要满足RFC2544建议的基本标准,即吞吐量、时延、丢包率外,随着…...
)
Connext DDS属性配置参考大全(1)
介绍属性QoS策略存储名称/值(字符串)对,可用于配置Connext DDS的某些参数,这些参数未通过正式的QoS策略公开。 属性QoS策略存储实体的名称/值对。名称和值都是字符串。在核心库用户手册的“Property QosPolicy(DDS Extension)”部分中找到有关RTI Connext DDS属性QoS的更…...
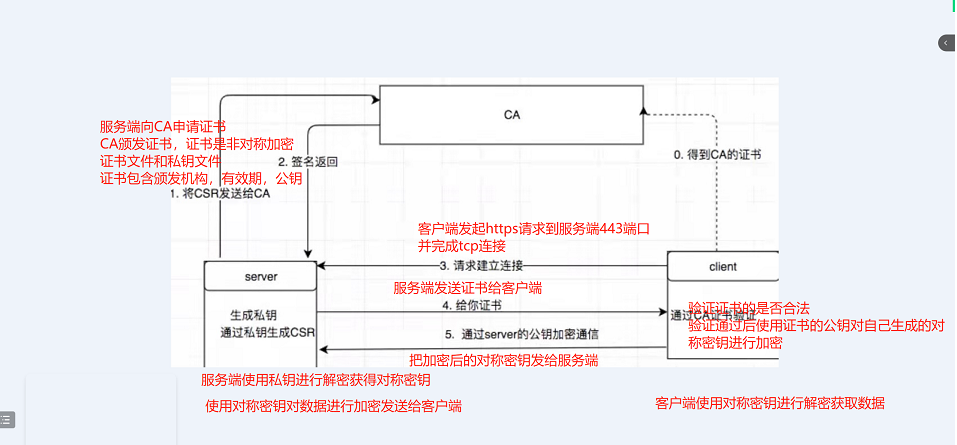
Docker安全
容器的安全性问题的根源在于容器和宿主机共享内核。如果容器里的应用导致Linux内核崩溃,那么整个系统可能都会崩溃。 与虚拟机是不同的,虚拟机并没有与主机共享内核,虚拟机崩溃一般不会导致宿主机崩溃 一、Docker 容器与虚拟机的区别 1、隔…...

刷题记录:牛客NC20279[SCOI2010]序列操作
传送门:牛客 题目描述: lxhgww最近收到了一个01序列,序列里面包含了n个数,这些数要么是0,要么是1,现在对于这个序列有五种变换操作和询问操作: 0 a b 把[a, b]区间内的所有数全变成0 1 a b 把[a, b]区间内的所有数全…...

Fluent Python 笔记 第 6 章 使用一等函数实现设计模式
虽然设计模式与语言无关,但这并不意味着每一个模式都能在每一门语言中使用。1996 年,Peter Norvig 在题为“Design Patterns in Dynamic Languages”(http://norvig.com/design- patterns/)的演讲中指出,Gamma 等人合著的《设计模式:可复用面…...

windbg-应用层实时调试
调试符号windbg使用一个或多个目录来存放符号条件,并使用环境变量_NT_SYMBOL_PATH来指向这些环境变量的位置,对操作系统内部模块的符号文件,一般用http://msdl.microsoft.com/download/symbols配置如下:SRV*C:\Symbols*http://msd…...

【Python语言基础】——Python NumPy 数组索引
Python语言基础——Python NumPy 数组索引 文章目录 Python语言基础——Python NumPy 数组索引一、Python NumPy 数组索引一、Python NumPy 数组索引 访问数组元素 数组索引等同于访问数组元素。 您可以通过引用其索引号来访问数组元素。 NumPy 数组中的索引以 0 开头,这意味…...
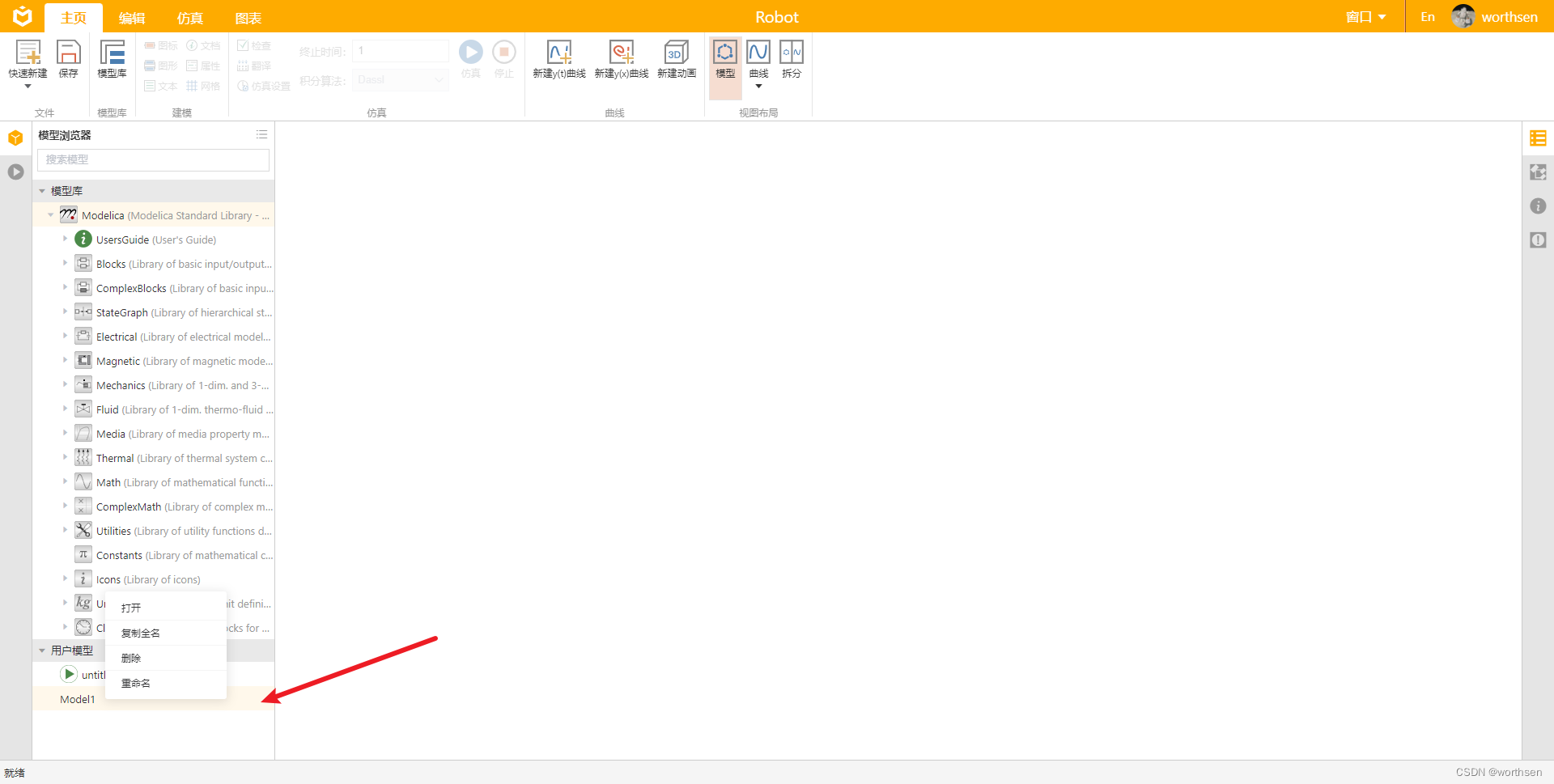
MWORKS--MoHub介绍
MWORKS--MoHub介绍1 介绍1.1 简介1.2 功能特征2 快速上手2.1 进入工作台2.2 新建仓库并进入建模空间2.3 建模进入建模工作空间加载模型库新建模型2.4 仿真2.5 后处理曲线、动画2.6 查看模型信息3 使用手册参考1 介绍 1.1 简介 MWORKS.MoHub 支持工业知识、经验、数据的模型化…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
