[USACO23JAN] Leaders B
题面翻译
题面描述
FJ 有 NNN 头奶牛,每一头奶牛的品种是根西岛 G 或荷斯坦 H 中的一种。
每一头奶牛都有一个名单,第 iii 头奶牛的名单上记录了从第 iii 头奶牛到第 EiE_iEi 头奶牛的所有奶牛。
每一种奶牛都有且仅有一位“领导者”,对于某一头牛 iii,如果它能成为“领导者”仅当它满足以下条件的至少一个:
-
其记录的名单上包含它的品种的所有奶牛。
-
其记录的名单上记录了另一品种奶牛的“领导者”。
请求出有多少对奶牛可能成为两种奶牛的领导者,保证存在至少一种。
数据范围
对于 100%100\%100% 的数据:1≤N≤2×105,i≤Ei≤N1\leq N\leq 2\times 10^5,i\leq E_i\leq N1≤N≤2×105,i≤Ei≤N。
题目描述
Farmer John has NNN cows (2≤N≤105)(2 \le N \le 10^5)(2≤N≤105). Each cow has a breed that is either Guernsey or Holstein. As is often the case, the cows are standing in a line, numbered 1⋯N1 \cdots N1⋯N in this order.
Over the course of the day, each cow writes down a list of cows. Specifically, cow iii
's list contains the range of cows starting with herself (cow iii) up to and including cow Ei(i≤Ei≤N)E_i(i \le E_i \le N)Ei(i≤Ei≤N).
FJ has recently discovered that each breed of cow has exactly one distinct leader. FJ does not know who the leaders are, but he knows that each leader must have a list that includes all the cows of their breed, or the other breed’s leader (or both).
Help FJ count the number of pairs of cows that could be leaders. It is guaranteed that there is at least one possible pair.
输入格式
The first line contains NNN.
The second line contains a string of length NNN
, with the ith character denoting the breed of the iii-th cow (G meaning Guernsey and H meaning Holstein). It is guaranteed that there is at least one Guernsey and one Holstein.
The third line contains E1⋯ENE_1 \cdots E_NE1⋯EN.
输出格式
Output the number of possible pairs of leaders.
样例 #1
样例输入 #1
4
GHHG
2 4 3 4
样例输出 #1
1
样例 #2
样例输入 #2
3
GGH
2 3 3
样例输出 #2
2
提示
Explanation for Sample 1
The only valid leader pair is (1,2)(1,2)(1,2). Cow 111’s list contains the other breed’s leader (cow 222). Cow 222’s list contains all cows of her breed (Holstein).
No other pairs are valid. For example, (2,4)(2,4)(2,4)
is invalid since cow 444’s list does not contain the other breed’s leader, and it also does not contain all cows of her breed.
Explanation for Sample 2
There are two valid leader pairs, (1,3)(1,3)(1,3) and (2,3)(2,3)(2,3).
Scoring
- Inputs 3−53-53−5: N≤100N \le 100N≤100
- Inputs 6−106-106−10: N≤3000N \le 3000N≤3000
- Inputs 11−1711-1711−17: N≤2×105N \le 2 \times 10^5N≤2×105
算法思想
本题核心就是分别求G和H的领导者个数,然后相乘得到最后答案。例如#2测试样例,G的领导者有两个,H的领导者有1个,那么他们的组合就有两对。
对于某一头牛来说,如果它能成为“领导者”仅当它满足以上述两个条件的至少一个。由于第二个条件依赖于第一个条件,因此我们可以先求出满足第一个条件的领导者。
暴力枚举(50分)
朴素做法就是两层循环,第一层循环枚举每一头奶牛iii,第二层循环枚举i到a[i]a[i]a[i],计算其本身品种的奶牛头数,判断其名单上是否记录了它的品种的所有奶牛。如果满足条件,就将第i头奶牛进行标记。
然后再标记第二种情况的领导者,也是两层循环,第一层循环枚举每一头奶牛iii,第二层循环枚举i到a[i]a[i]a[i],判断这之间是否存在另一种奶牛的领导者,如果存在则标记。
最后统计两种奶牛领导者的数量,将其相乘就是最终答案
时间复杂度
时间复杂度为O(n2)O(n^2)O(n2)。
代码实现
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10;
char s[N];
int a[N], g[N], h[N];
int main()
{int n;cin >> n;cin >> s + 1;int s1 = 0, s2 = 0;for(int i = 1; i <= n; i ++){if(s[i] == 'G') s1 ++;else s2 ++;}for(int i = 1; i <= n; i ++) cin >> a[i];//处理第一种领导者:其记录的名单上包含它的品种的所有奶牛for(int i = 1; i <= n; i ++){int gg = 0, hh = 0;for(int j = i; j <= a[i]; j ++){if(s[j] == 'G') gg ++;else hh ++;}if(s[i] == 'G' && gg == s1) g[i] = 1; //标记为领导者else if(s[i] == 'H' && hh == s2) h[i] = 1; //标记为领导者}//处理第二种领导者:其记录的名单上记录了另一品种奶牛的“领导者”。for(int i = 1; i <= n; i ++){for(int j = i; j <= a[i]; j ++){if(s[i] == 'G' && h[j] == 1){g[i] = 1;break;}else if(s[i] == 'H' && g[j] == 1){h[i] = 1;break;}}}int c1 = 0, c2 = 0;for(int i = 1; i <= n; i ++)if(g[i]) c1 ++;for(int i = 1; i <= n; i ++)if(h[i]) c2 ++;cout << c1 * c2 << endl;
}
前缀和优化(100分)
朴素做法的问题在于使用了两层循环,其实第二层循环可以使用前缀和进行优化,用空间换时间。
s1[]前缀和数组,s1[i]表示前i个字符中字符G的个数s2[]前缀和数组,s2[i]表示前i个字符中字符H的个数gs[]前缀和数组,gs[i]表示前i头牛中第一类G品种领导者的数量hs[]前缀和数组,hs[i]表示前i头牛中第一类H品种领导者的数量
时间复杂度
朴素做法的时间复杂度为O(n)O(n)O(n)。
代码实现
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10;
char s[N];
int e[N], s1[N], s2[N], g[N], h[N], gs[N], hs[N];
int main()
{int n;cin >> n;cin >> s + 1;for(int i = 1; i <= n; i ++) cin >> e[i];//s1[i]前缀和, 表示前i个字符中字符G的个数//s2[i]前缀和, 表示前i个字符中字符H的个数for(int i = 1; i <= n; i ++){s1[i] = s1[i - 1], s2[i] = s2[i - 1];if(s[i] == 'G') s1[i] ++;else s2[i] ++;}//处理第一种领导者:其记录的名单上包含本身的品种的所有奶牛for(int i = 1; i <= n; i ++){//gg表示从i到e[i]位置所有G的个数//hh表示从i到e[i]位置所有H的个数int gg = s1[e[i]] - s1[i - 1], hh = s2[e[i]] - s2[i - 1];//其记录的名单上包含本身的品种的所有奶牛if(s[i] == 'G' && gg == s1[n]) g[i] = 1; //将i位置标记为'G'的领导者else if(s[i] == 'H' && hh == s2[n]) h[i] = 1;//将i位置标记为'H'的领导者}//gs[i]前缀和,表示前i个奶牛中G的第一种领导者个数//hs[i]前缀和,表示前i个奶牛中H的第一种领导者个数for(int i = 1; i <= n; i ++){gs[i] = gs[i - 1], hs[i] = hs[i - 1];if(g[i]) gs[i] ++;if(h[i]) hs[i] ++;}//ga表示G的第一种领导者个数,ha表示H的第一种领导者个数int ga = gs[n], ha = hs[n];//处理第二种领导者:其记录的名单上记录了另一品种奶牛的“领导者”。for(int i = 1; i <= n; i ++){ //其记录的名单上记录了另一品种奶牛的领导者if(s[i] == 'G' && (hs[e[i]] - hs[i - 1]) != 0) ga ++;else if(s[i] == 'H' && (gs[e[i]] - gs[i - 1]) != 0) ha ++;}cout << ga * ha << endl;
}
相关文章:

[USACO23JAN] Leaders B
题面翻译 题面描述 FJ 有 NNN 头奶牛,每一头奶牛的品种是根西岛 G 或荷斯坦 H 中的一种。 每一头奶牛都有一个名单,第 iii 头奶牛的名单上记录了从第 iii 头奶牛到第 EiE_iEi 头奶牛的所有奶牛。 每一种奶牛都有且仅有一位“领导者”,对…...
C++模板初阶
C模板初阶泛型编程函数模板概念函数模板格式函数模板原理函数模板的实例化模板参数的匹配原则类模板类模板的定义格式类模板的实例化泛型编程 我们前面学习了C的函数重载功能,那么我们如何实现一个通用的交换函数呢,比如:我传入int就是交换intÿ…...

文献阅读:Scaling Instruction-Finetuned Language Models
文献阅读:Scaling Instruction-Finetuned Language Models 1. 文章简介2. 实验 1. 数据集 & 模型 1. 数据集考察2. 使用模型 2. scale up对模型效果的影响3. CoT对模型效果的影响4. 不同模型下Flan的影响5. 开放接口人工标注指标 3. 结论 文献链接:…...

gpt草稿
ChatgptWhatChatGPT(全名:Chat Generative Pre-trained Transformer [2])是由OpenAI开发的一个人工智能聊天机器人程序,于2022年11月推出。该程序使用基于GPT-3.5架构的大型语言模型并通过强化学习进行训练。ChatGPT里面有两个词&…...

mysal第三次作业
1、显示所有职工的基本信息。 2、查询所有职工所属部门的部门号,不显示重复的部门号。 3、求出所有职工的人数。 4、列出最高工和最低工资。 5、列出职工的平均工资和总工资。 6、创建一个只有职工号、姓名和参加工作的新表,名为工作日期表…...
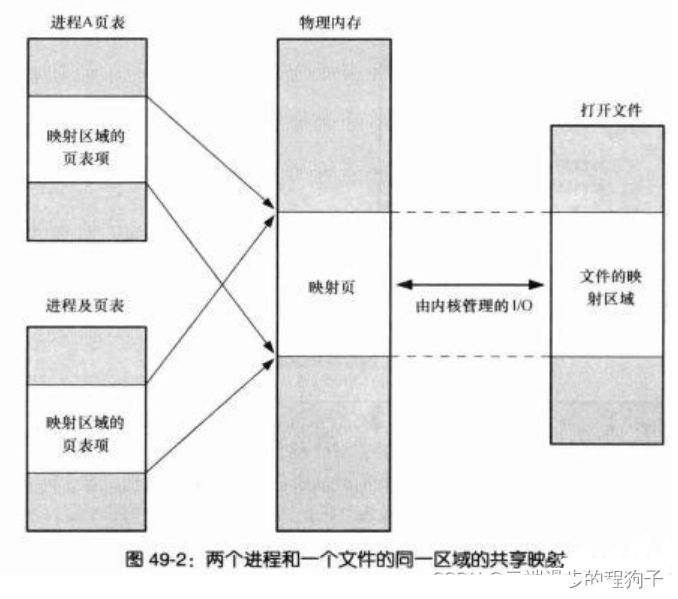
分页和mmap
文章目录一、内存分页1、基本概念2、分页机制下,虚拟地址和物理地址是如何映射的?3、快表(TLB)二、mmap基本原理和分类一、内存分页 1、基本概念 CPU并不是直接访问物理内存地址,而是通过虚拟地址空间来间接的访问物理内存地址。 页&#x…...
C++之异常处理
异常异常是面向对象语言处理错误的一种方式。当一个函数出现自己无法处理的错误时,可以抛出异常,然后输的直接或者间接调用者处理这个错误。语法捕获全部的异常try {//可能抛出异常的代码//throw异常对象 } catch(...) {//不管什么异常,都在这…...
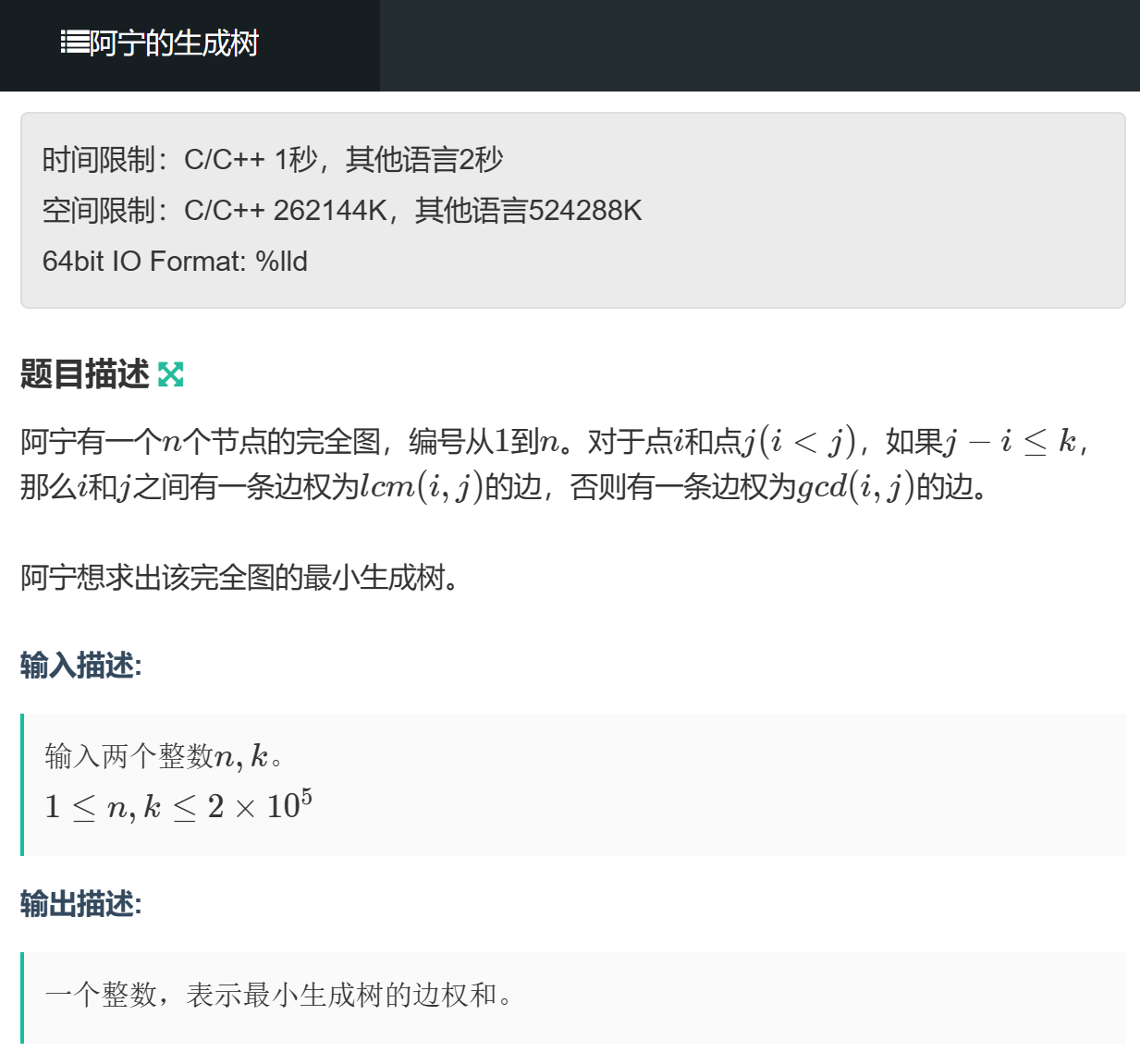
牛客寒假集训营6 E 阿宁的生成树
E-阿宁的生成树_2023牛客寒假算法基础集训营6 (nowcoder.com)开始慢慢补牛牛的题题意:最小生成树质数距离思路:最小生成树一共就两种算法,我们考虑Prim的过程初始连通块是1,然后考虑拿1和其他的结点连边当j-i<k时边权是gcd&…...
)
嵌入式C基础知识(10)
C语言如何实现一个频繁使用短小函数,C如何实现?C语言可以使用宏定义实现一个短小函数,如下面例子所示。但是宏定义语句不会进行检查,并且对书写格式有过分的讲究。比如MAX和括号之间不能有空格,每个参数都要放在括号里…...

TC3xx FlexRay™ 协议控制器 (E-Ray)-01
1 FlexRay™ 协议控制器 (E-Ray) E-Ray IP 模块根据为汽车应用开发的 FlexRay™ 协议规范 v2.1 执行通信【performs communication according to the FlexRay™ 1) protocol specification v2.1】。使用最大指定时钟,比特率可以编程为高达 10 Mbit/s 的值。连接到物…...

优劣解距离法TOPSIS——清风老师
TOPSIS法是一种常用的综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。 基本过程为先将原始数据矩阵统一指标类型(一般正向化处理)得到正向化的矩阵,再对正向化的矩阵进行标准化处理…...
【Unity3D】Shader常量、变量、结构体、函数
1 源码路径 Unity Shader 常量、变量、结构体、函数一般可以在 Unity Editor 安装目录下面的【Editor\Data\CGIncludes\UnityShader】目录下查看源码,主要源码文件如下: UnityCG.cgincUnityShaderUtilities.cgincUnityShaderVariables.cginc 2 Shader 常…...

LeetCode 刷题系列 -- 496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。对于每个 0 < i < nums1.length ,找出满…...
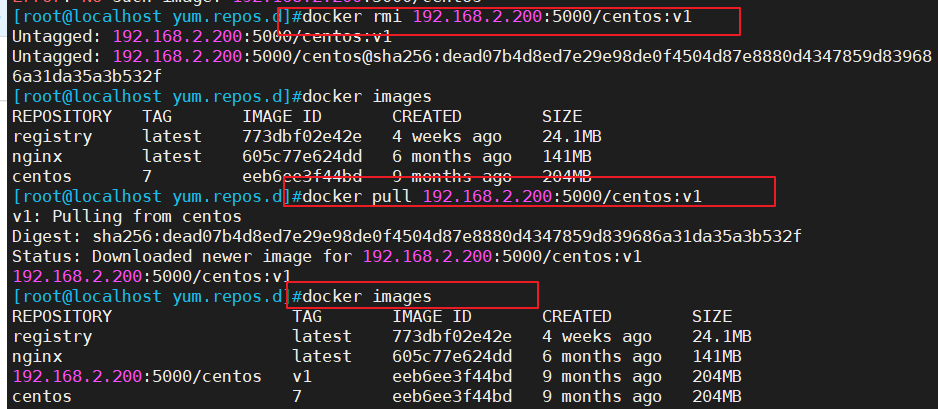
Docker 搭建本地私有仓库
一、搭建本地私有仓库有时候使用Docker Hub这样的公共仓库可能不方便,这种情况下用户可以使用registry创建一个本地仓库供私人使用,这点跟Maven的管理类似。使用私有仓库有许多优点:1)节省网络带宽,针对于每个镜像不用…...

XML中的CDATA且mybatis中特殊字符转义
如果想看如果CDATA在mybatis的xml文件中使用的可以直接跳转。 CDATA1 XML中的CDATA1.1 为什么叫CDATA1.2 CDATA在XML中的语法1.3 CDATA在XML中的例子1.4 CDATA规则2 Mybatis中的CDATA2.1 Mybatis中使用XML转义序列转义2.2 Mybatis中使用CDATA转义2.3 mybatis中使用CDATA需注意的…...

位运算 | 1356. 根据数字二进制下 1 的数目排序
LeetCode 1356. 根据数字二进制下 1 的数目排序 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中数字 1 的数目升序排序。如果存在多个数字二进制中 1 的数目相同,则必须将它们按照数值大小升序排列。 文章讲解https://www.programmercarl.com/1356.%…...

React Hooks之useState详解
1. 什么是Hooks? React官方简介:Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。 本文中讲解的useState就是React中的其中一个Hook。 2. useState useState 通过在函数组件里调用它来满足给组件添…...

选购交换机的参数依据和主要的参数指标详解
如何选购交换机?用什么交换机?在选购交换机时交换机的优劣无疑十分的重要,而交换机的优劣要从总体构架、性能和功能三方面入手。交换机选购时。性能方面除了要满足RFC2544建议的基本标准,即吞吐量、时延、丢包率外,随着…...
)
Connext DDS属性配置参考大全(1)
介绍属性QoS策略存储名称/值(字符串)对,可用于配置Connext DDS的某些参数,这些参数未通过正式的QoS策略公开。 属性QoS策略存储实体的名称/值对。名称和值都是字符串。在核心库用户手册的“Property QosPolicy(DDS Extension)”部分中找到有关RTI Connext DDS属性QoS的更…...
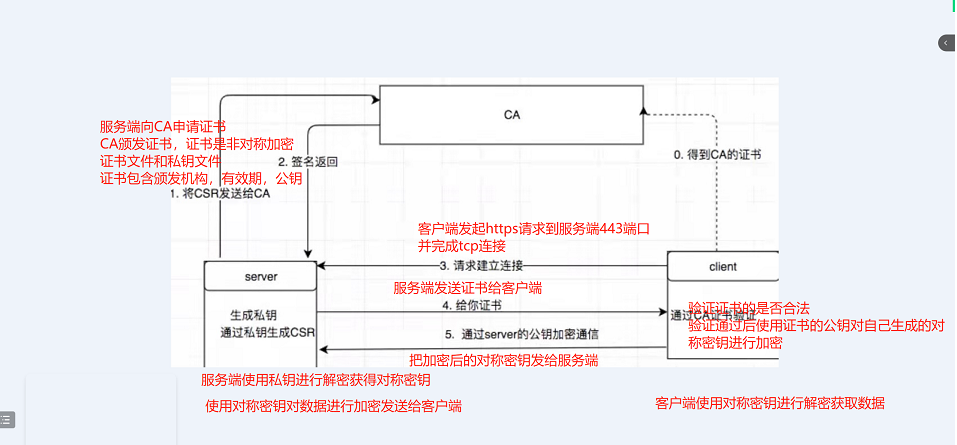
Docker安全
容器的安全性问题的根源在于容器和宿主机共享内核。如果容器里的应用导致Linux内核崩溃,那么整个系统可能都会崩溃。 与虚拟机是不同的,虚拟机并没有与主机共享内核,虚拟机崩溃一般不会导致宿主机崩溃 一、Docker 容器与虚拟机的区别 1、隔…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
