当前位置： 首页 > news >正文

小程序按钮分享

news 2026/2/10 2:14:11

 使用button设置：

open-type="share"：来微信分享；

html：

<button open-type="share"></button>

相关文章：

小程序按钮分享

使用button设置&#xff1a; open-type"share"&#xff1a;来微信分享&#xff1b; html&#xff1a; <button open-type"share"></button>...

编程日记 2024/8/2 7:40:44

多模态多智能体，在实现系统2（深思熟虑）方面的探索

多模态和多智能体&#xff0c;在系统2&#xff08;深思熟虑&#xff09;方面的探索 提出背景理性的定义为什么理性定义是四大基本原则&#xff0c;而不是其他数量&#xff0c;又为何是这四个&#xff0c;而不是其他&#xff1f;理性 不等于 推理 通过多模态多智能体系统增强理性…...

编程日记 2024/8/2 7:39:43

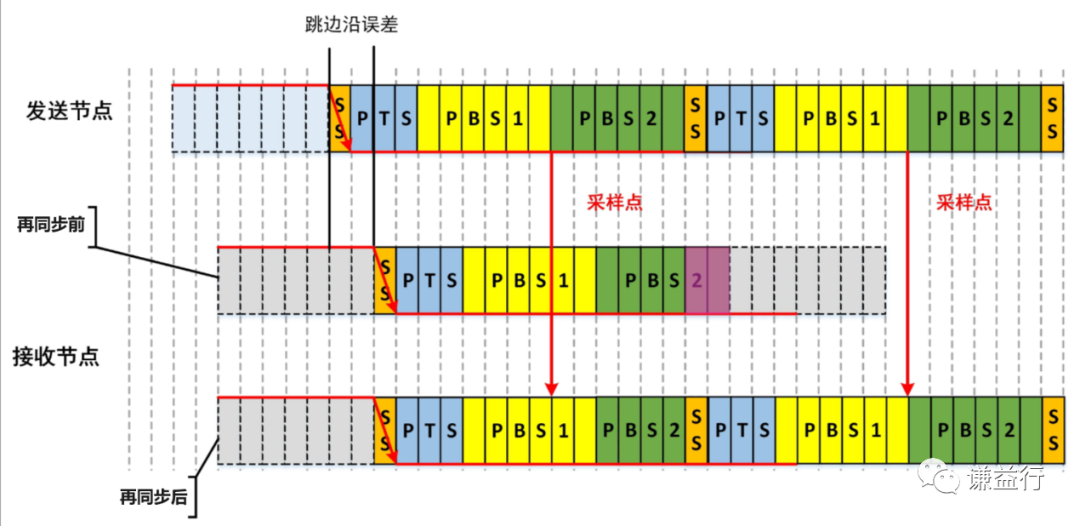
【CAN通讯系列8】如何准确接收数据？

在 【CAN通讯系列7】波特率是什么&#xff1f;已经介绍了CAN位时间和采样点等概念&#xff0c;每1位由同步段(SS)、传播时间段(PTS)、相位缓冲段1(PBS1)和相位缓冲段2(PBS2)四个段组成&#xff0c;这个也成为位时序&#xff0c;采样点位置处于PBS1和PBS2的交界处&#xff0c;如…...

编程日记 2024/8/2 7:38:42

RabbitMQ知识总结（基本概念）

文章收录在网站&#xff1a;http://hardyfish.top/ 文章收录在网站&#xff1a;http://hardyfish.top/ 文章收录在网站&#xff1a;http://hardyfish.top/ 文章收录在网站&#xff1a;http://hardyfish.top/ 基本概念 Producer&#xff1a; 消息的生产者&#xff0c;是一个向…...

编程日记 2024/8/2 7:35:39

Prel语言入门学习：一篇全面的指南

引言 在编程语言的海洋中&#xff0c;Prel是一个较少人知的新星。作为一种专为数据处理和分析设计的语言&#xff0c;Prel结合了现代编程语言的简洁性与功能性&#xff0c;提供了一种独特的解决方案&#xff0c;尤其适用于数据科学家和分析师。本文将详细介绍Prel语言的基础&am…...

编程日记 2024/8/2 7:33:37

在云服务器上自动化部署项目，jenkins和gitee

▮全文概述 在编写项目时&#xff0c;很头大的事情就是需要自己手动的上传jar包到服务器上启动。如果出现一点bug&#xff0c;就要重头上传和启动。这是一件很烦的事情&#xff0c;所以&#xff0c;可以使用jenkins和gitee实现项目的自动部署 ▮全流程 在本地提交代码到gitee …...

编程日记 2024/8/2 7:32:36

python 参数输入

在 Python 中&#xff0c;参数输入通常有多种方式&#xff0c;这取决于你要从何处获取参数。以下是几种常见的方法&#xff1a; 1. 命令行参数 使用 sys.argv 获取命令行参数&#xff0c;或者使用 argparse 模块进行更复杂的参数解析。 示例 1: 使用 sys.argv import sys# …...

编程日记 2024/8/2 7:30:34

Spring面试篇章——Spring基本概述

Spring 的基本概述 Spring学习的核心内容—一图胜千言 IOC&#xff1a;控制反转&#xff0c;可以管理 Java 对象AOP&#xff1a;切面编程JDBCTemplate&#xff1a;是Spring提供一套访问数据库的技术&#xff0c;应用性强&#xff0c;相对好理解声明式事务&#xff1a;基于IOC …...

编程日记 2024/8/2 7:28:31

股票预测模型中注意力多层Attention RNN LSTM 的应用

全文链接&#xff1a;https://tecdat.cn/?p37152 原文出处&#xff1a;拓端数据部落公众号 Attention 机制是一种在神经网络处理序列数据时极为关键的技术&#xff0c;它赋予了模型“聚焦”能力&#xff0c;能够自动评估输入序列中各部分的重要性。通过为序列中的每个元素分…...

编程日记 2024/8/2 7:25:28

C语言 | Leetcode C语言题解之第313题超级丑数

题目&#xff1a; 题解&#xff1a; int nthSuperUglyNumber(int n, int* primes, int primesSize) {long dp[n 1];int pointers[primesSize];for (int i 0; i < primesSize; i) {pointers[i] 0;}long nums[primesSize];for (int i 0; i < primesSize; i) {nums[i] …...

编程日记 2024/8/2 7:23:26

PHP健身微信小程序系统源码

&#x1f3cb;️‍♀️健身新潮流&#xff01;解锁“健身微信小程序”的全方位塑形秘籍 &#x1f4f1;开篇&#xff1a;掌中健身房&#xff0c;随时随地动起来 你还在为找不到合适的健身场地或教练而烦恼吗&#xff1f;是时候告别这些束缚&#xff0c;拥抱“健身微信小程序”…...

编程日记 2024/8/2 7:21:23

树组件 el-tree 数据回显

树组件 el-tree 数据回显 树型结构的数据回显问题&#xff1a; 这里我只放了核心代码&#xff0c;主要是如何获取选中的树节点的id集合和如何根据树节点的id集合回显数据 大家根据需要自行更改&#xff01; <el-tree ref"authorityRef" node-key"id" …...

编程日记 2024/8/2 7:19:20

54、PHP 实现希尔排序

题目&#xff1a; PHP 实现希尔排序 描述&#xff1a; 思路分析&#xff1a;希尔排序是基于插入排序的&#xff0c;区别在于插入排序是相邻的一个个比较&#xff08;类似于希尔中h1的情形&#xff09;&#xff0c;而希尔排序是距离h的比较和替换。 希尔排序中一个常数因子n&a…...

编程日记 2024/8/2 7:17:18

linux 虚拟机解压arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2并arm-linux-gcc

解压到当前目录&#xff1a;tar -jxvf arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2解压到指定目录&#xff1a;tar -jxvf arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2 -C /xx/xxx/xxx-C大写&#xff0c;后面接要解压的路径解压后得到一个 opt文件夹 在/usr/local/bin 下创建新的…...

编程日记 2024/8/2 7:16:17

泛化的最近点迭代法（Generalized-ICP）

Generalized-ICP算法是由斯坦福大学的Aleksandr V. Segal、Dirk Haehnel和Sebastian Thrun提出的&#xff0c;于2009年在Robotics science and system会议上发表。 GICP是一种ICP算法的变体&#xff0c;其原理与ICP算法相同&#xff0c;之所以称为泛化的ICP算法是因为大多数ICP…...

编程日记 2024/8/2 7:13:13

Java | Leetcode Java题解之第313题超级丑数

题目&#xff1a; 题解&#xff1a; class Solution {public int nthSuperUglyNumber(int n, int[] primes) {int[] dp new int[n 1];int m primes.length;int[] pointers new int[m];int[] nums new int[m];Arrays.fill(nums, 1);for (int i 1; i < n; i) {int minN…...

编程日记 2024/8/2 7:12:12

单细胞数据整合-去除批次效应harmony和CCA (学习)

目录 单细胞批次效应学习 定义 理解 常用的去批次方法-基于Seurat 1&#xff09; Seurat-integration&#xff08;CCA&#xff09; 2&#xff09; Seurat-harmony 去批次代码 ①Seurat-integration&#xff08;CCA&#xff09; ②Seurat-harmony 单细胞批次效应学习 …...

编程日记 2024/8/2 7:11:11

MuRF代码阅读

对图像Size的处理, 以适应Transformer 在MVSPlat 当中使用 Center_Crop 裁剪图像&#xff0c;适用于 Transformer 的32 倍数&#xff0c; 其中 焦距 f 不变化&#xff0c;只改变 cx,cy.MuRF 直接对图像进行 插值&#xff0c;合成理想的 size. 根据 ori_size 和 inference_size…...

编程日记 2024/8/2 7:10:10

pycharm无法导入pyside2模块；“ModuleNotFoundError: No module named ‘PySide2“

参考博客&#xff1a; 1&#xff09;pycharm中配置pyqt designer和pyside2【功能是在pycharm中可以打开designer,并且可以把.ui文件转换为.py文件】 https://blog.csdn.net/kuntliu/article/details/117219237 2&#xff09;.ui转化为.py后&#xff0c;点击运行&#xff0c;报错…...

编程日记 2024/8/2 7:08:08

c语言指针中“数组名的理解”以及“一维数组传参”的本质

数组名的理解 数组名就是数组首元素的地址。 例如&#xff1a;输入一个数组的所有元素&#xff0c;再打印出来。 另一种写法 以上可以看出&#xff1a;*arri&#xff09; arr[i] 也即是&#xff1a;*(iarr)i[arr] 本质上无区别 1&#xff1a;数组就是数组&#xff0c;是一块…...

编程日记 2024/8/2 7:07:06

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

RocketMQ延迟消息机制

两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数&#xff0c;对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后&#xf…...

编程新知 2026/2/8 21:59:25

椭圆曲线密码学(ECC)

一、ECC算法概述 椭圆曲线密码学&#xff08;Elliptic Curve Cryptography&#xff09;是基于椭圆曲线数学理论的公钥密码系统&#xff0c;由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA&#xff0c;ECC在相同安全强度下密钥更短&#xff08;256位ECC ≈ 3072位RSA…...

编程新知 2025/10/1 22:26:06

安宝特方案丨XRSOP人员作业标准化管理平台：AR智慧点检验收套件

在选煤厂、化工厂、钢铁厂等过程生产型企业&#xff0c;其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进&#xff0c;需提前预防假检、错检、漏检&#xff0c;推动智慧生产运维系统数据的流动和现场赋能应用。同时&#xff0c;…...

编程新知 2026/2/5 17:57:20

【解密LSTM、GRU如何解决传统RNN梯度消失问题】

解密LSTM与GRU&#xff1a;如何让RNN变得更聪明&#xff1f; 在深度学习的世界里&#xff0c;循环神经网络&#xff08;RNN&#xff09;以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而&#xff0c;传统RNN存在的一个严重问题——梯度消失&#…...

编程新知 2025/12/24 1:45:14

MVC 数据库

MVC 数据库 引言 在软件开发领域，Model-View-Controller（MVC）是一种流行的软件架构模式，它将应用程序分为三个核心组件：模型（Model）、视图（View）和控制器（Controller）。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系，以…...

编程新知 2025/10/30 4:58:11

spring：实例工厂方法获取bean

spring处理使用静态工厂方法获取bean实例&#xff0c;也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下&#xff1a; 定义实例工厂类&#xff08;Java代码&#xff09;&#xff0c;定义实例工厂&#xff08;xml&#xff09;&#xff0c;定义调用实例工厂&#xff…...

编程新知 2025/11/25 22:46:30

AI书签管理工具开发全记录（十九）：嵌入资源处理

1.前言 &#x1f4dd; 在上一篇文章中&#xff0c;我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源&#xff0c;方便后续将资源打包到一个可执行文件中。 2.embed介绍 &#x1f3af; Go 1.16 引入了革命性的 embed 包&#xff0c;彻底改变了静态资源管理的…...

编程新知 2026/1/30 16:24:23

云原生安全实战：API网关Kong的鉴权与限流详解

&#x1f525;「炎码工坊」技术弹药已装填&#xff01; 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关&#xff08;API Gateway&#xff09; API网关是微服务架构中的核心组件&#xff0c;负责统一管理所有API的流量入口。它像一座…...

编程新知 2026/2/1 6:24:16

Git常用命令完全指南：从入门到精通

Git常用命令完全指南&#xff1a;从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

编程新知 2025/10/3 0:40:01