48天强训 Day1 JavaOj
48天强训 & Day1 & JavaOj
1. 编程题1 - 组队竞赛
组队竞赛_牛客笔试题_牛客网 (nowcoder.com)
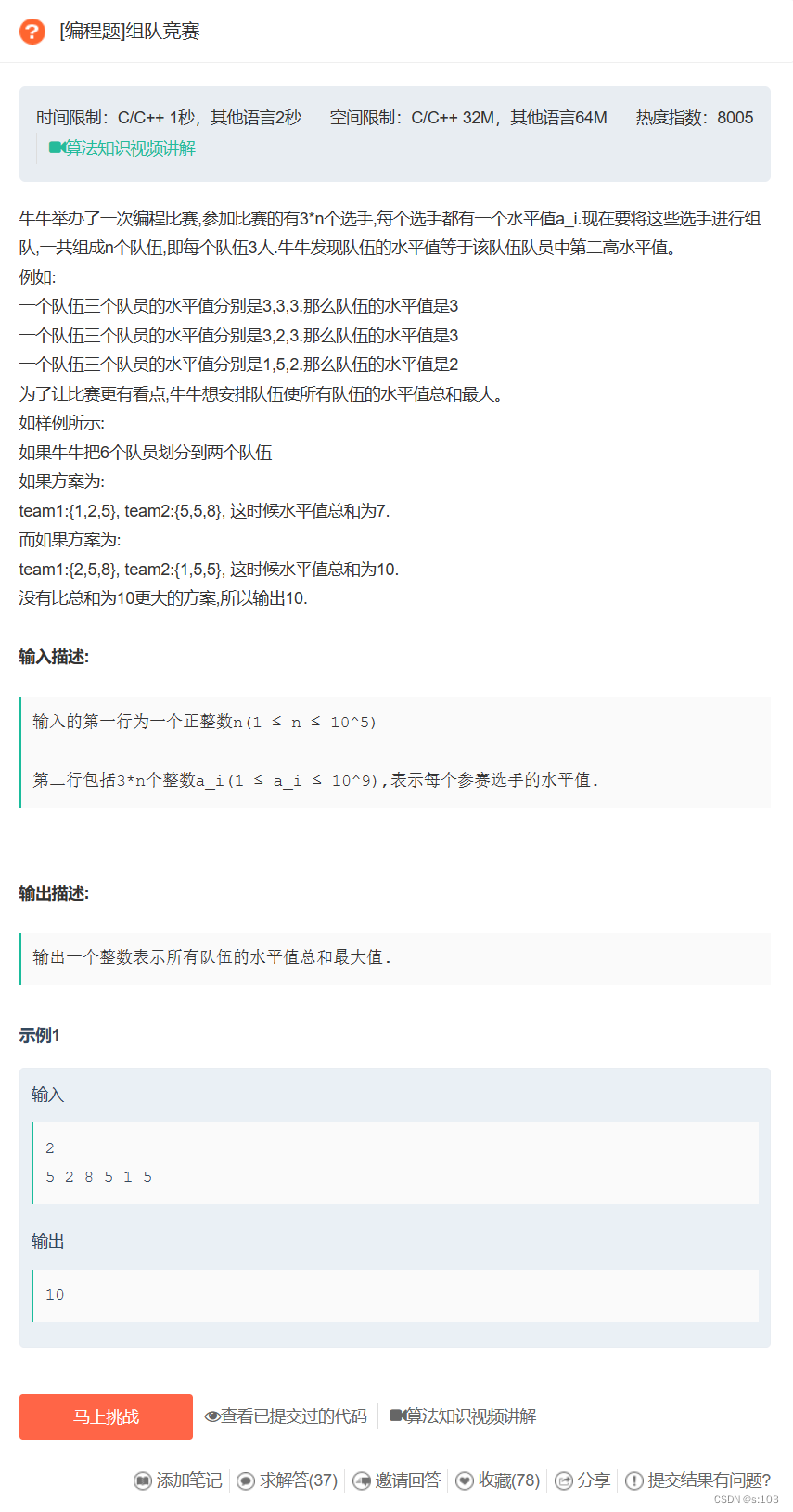
1.1 读题

1.2 算法思想基础
- 我们应该尽量的让每一个队伍的中间值都最大化~
- 我们应该尽量的让每一个队伍的最小值都足够小~
- 前33%的不应该都作为每个队伍的最大值~
- 接下来我将讲解每个位置应该如何选组员~
- 但是这里我要说一个前提
- 首先,我们需要把所有人进行一个排序~
- 分为前三分之一,中三分之一,后三分之一
- 后三分之一为整体水平排名靠后的~
1.2.1 后三分之一
- 我们要想让一个队伍的最小值足够小
- 那么我们可以让那么就选整体水平的后三分之一
- 事实也是如此~
证明:(反证法)
- 首先:
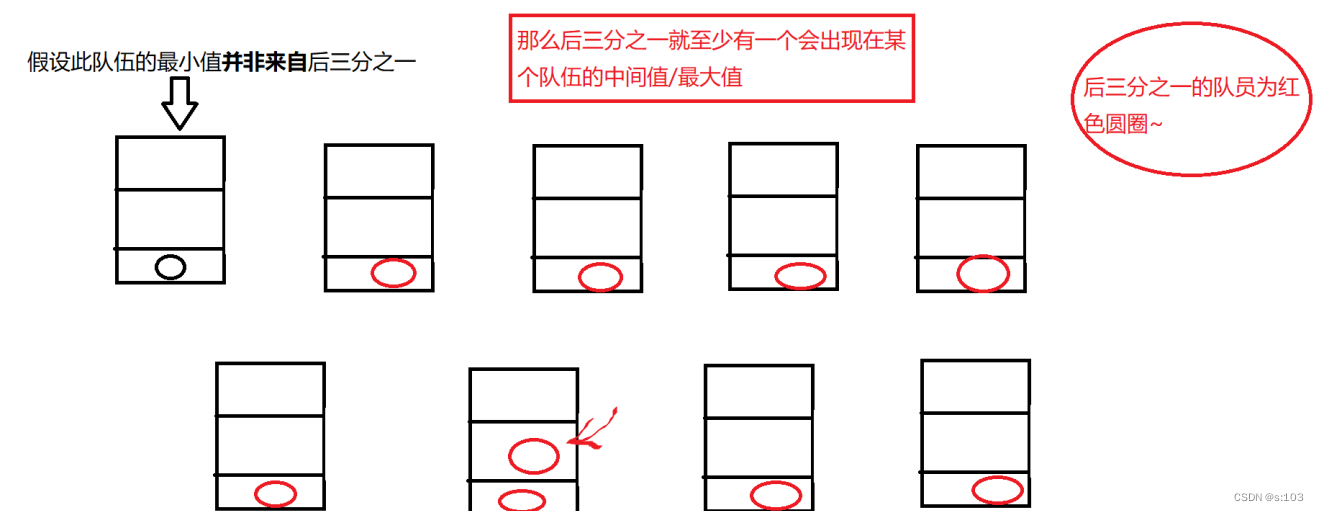
- 其次:
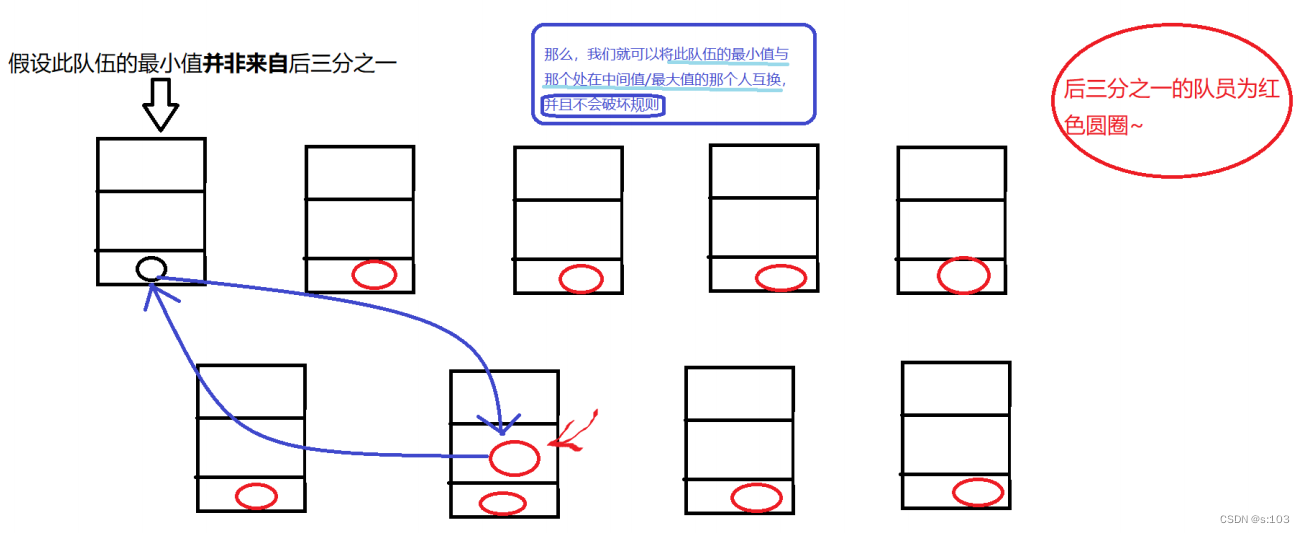
- 得出结论:
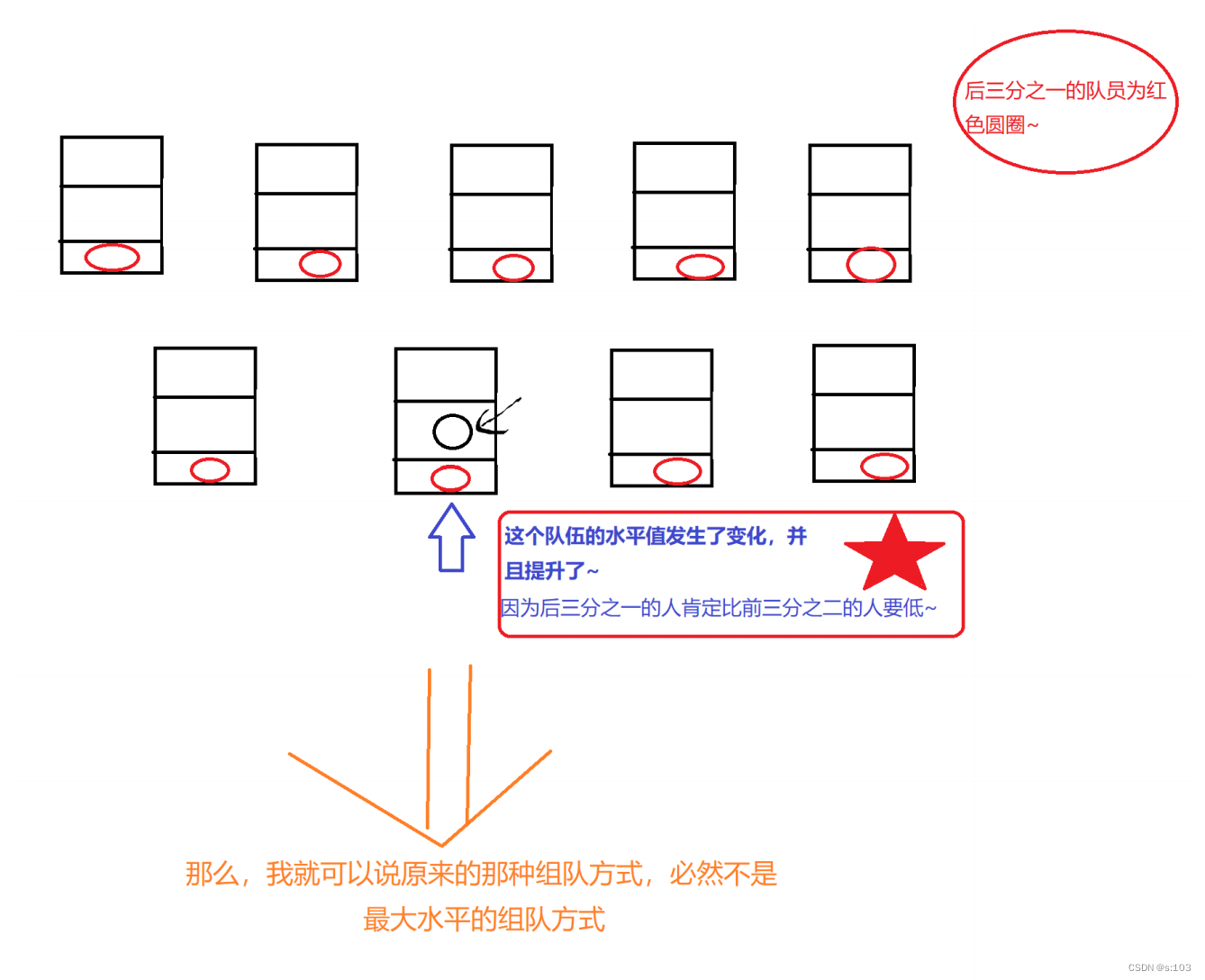
- 也就是说,为了让组队水平最大化,我们应该让每个队伍的最小值,要在整体的后三分之一里去选~
- 并且这么选都可以,因为最大值和中间值都会比最小值大,并且队伍的水平不受最小值影响~
1.2.2 前三分之二
- 我们确定了每个队伍的最小值后,紧接着就要确定一个一个的队伍了~
- 切记,并不能让前三分之一的人都作为每个队伍的最大值,这样非常影响总体水平~
- 原理跟刚才差不多,可以用反证法证明~
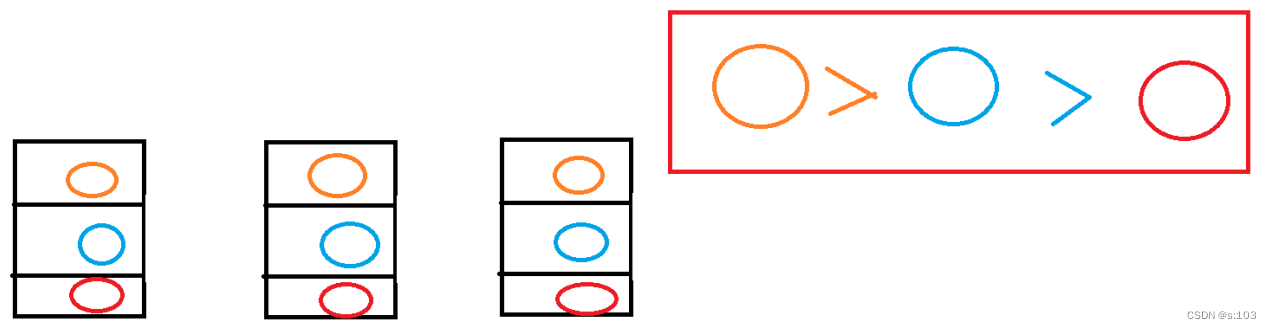
- 其实这样排是有可能做对的
- 但是,肯定是有漏洞的~
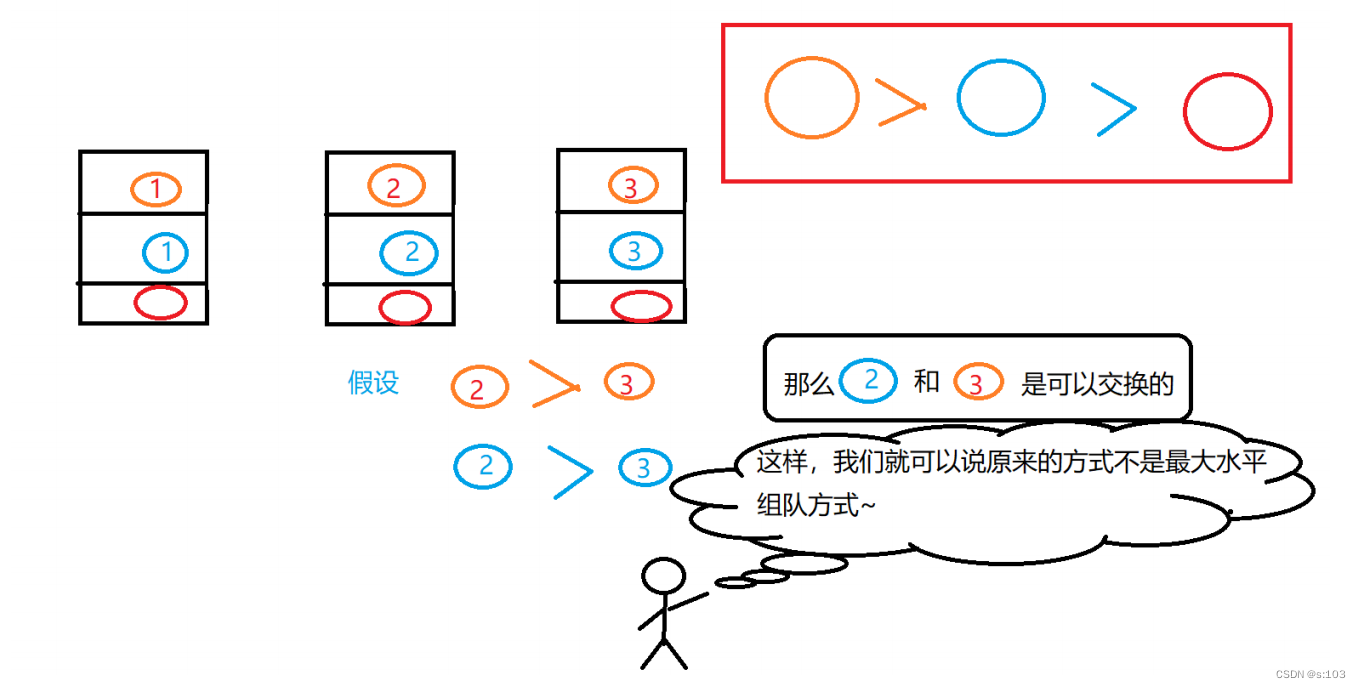
- 而正确的思想是,一个一个队伍的去确定,每次确定都让这个队伍水平最大化~
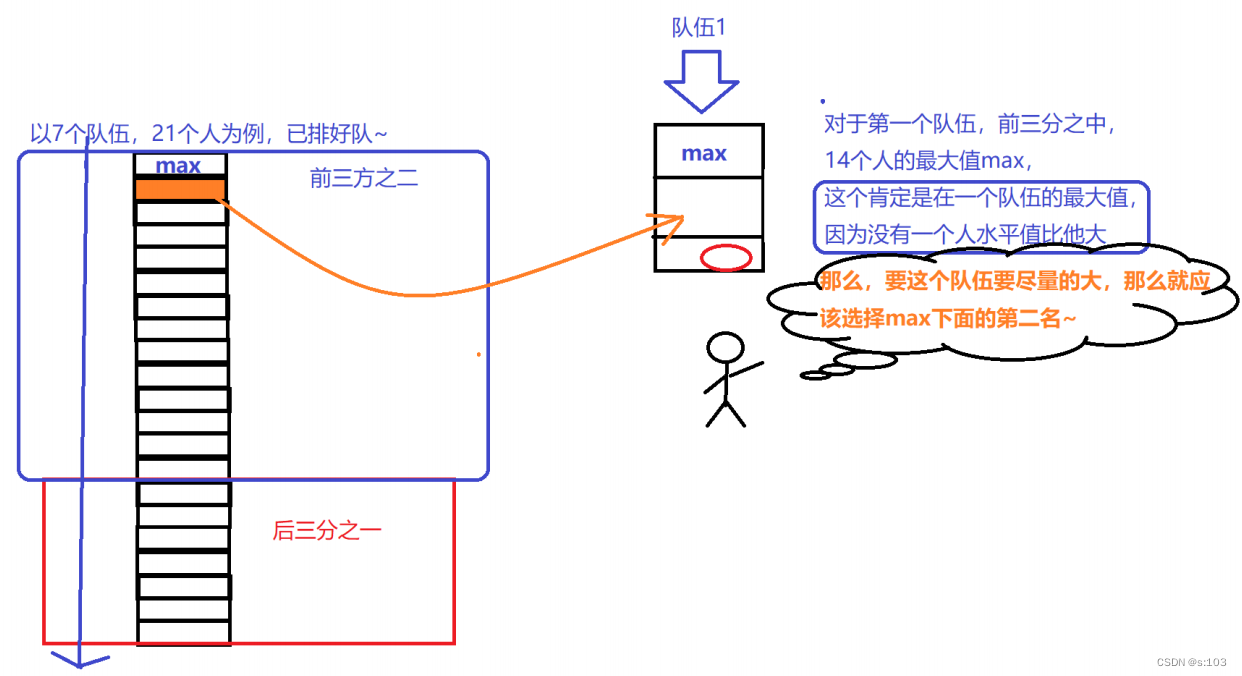
- 对于第二个队伍
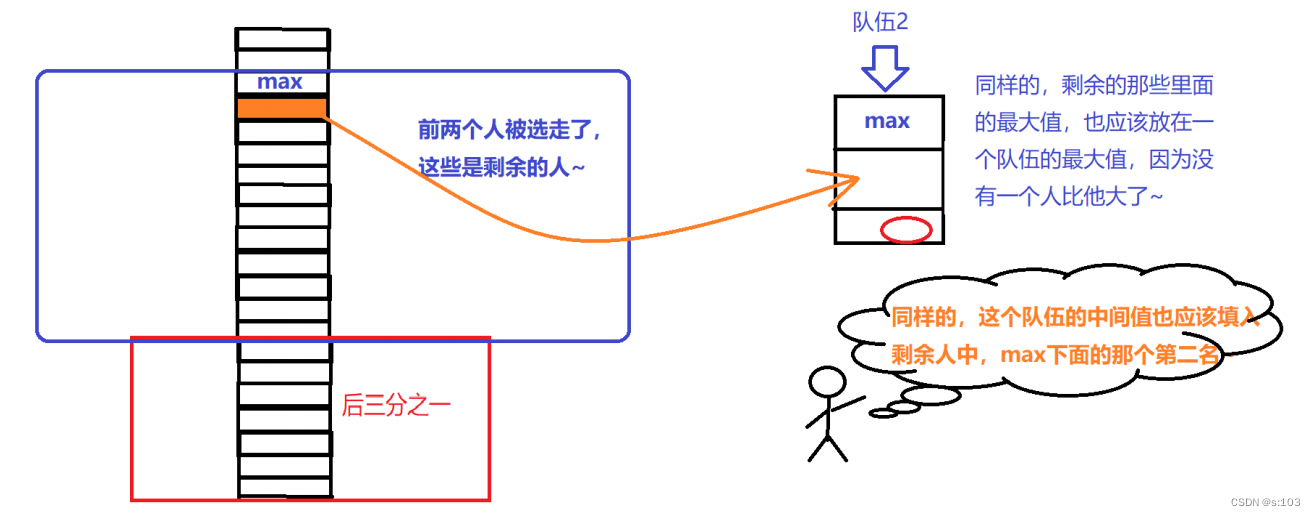
- 以此类推~
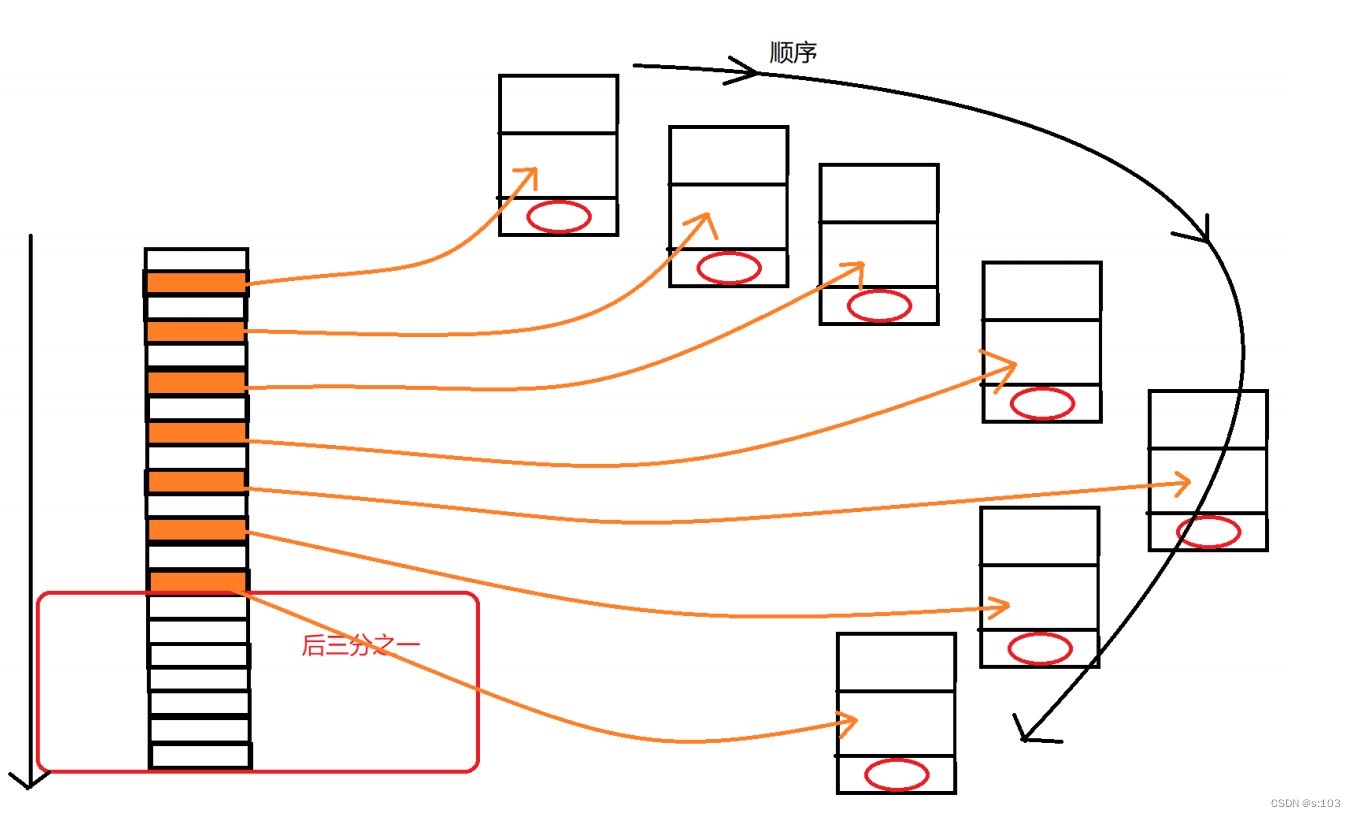
- 所以,最大水平组队方式就是这样的
- 水平总和最大值为:
- 假设有n个队伍
- 所有人从大到小排为 a3n
- 水平总和值为Sn
- 则Snmax = a2 + a4 + a6 + ······ + a2n
1.3 代码设计
- n为队伍的个数
- 那么我们只需要知道前2n名
- topK问题
- 用优先级队列 - 堆
- 前k大,用小根堆
- 每次去梢(poll),就是去掉最小值
- 这里就相当于去掉a2n、a2n-1 ······
- 按照上面的算法,我们可以从a2n + a2n-2 + ······ + a4 + a2
- 即从后往前加
- 当然也可以直接用各种排序方式去排序,然后按照下标依次相加~
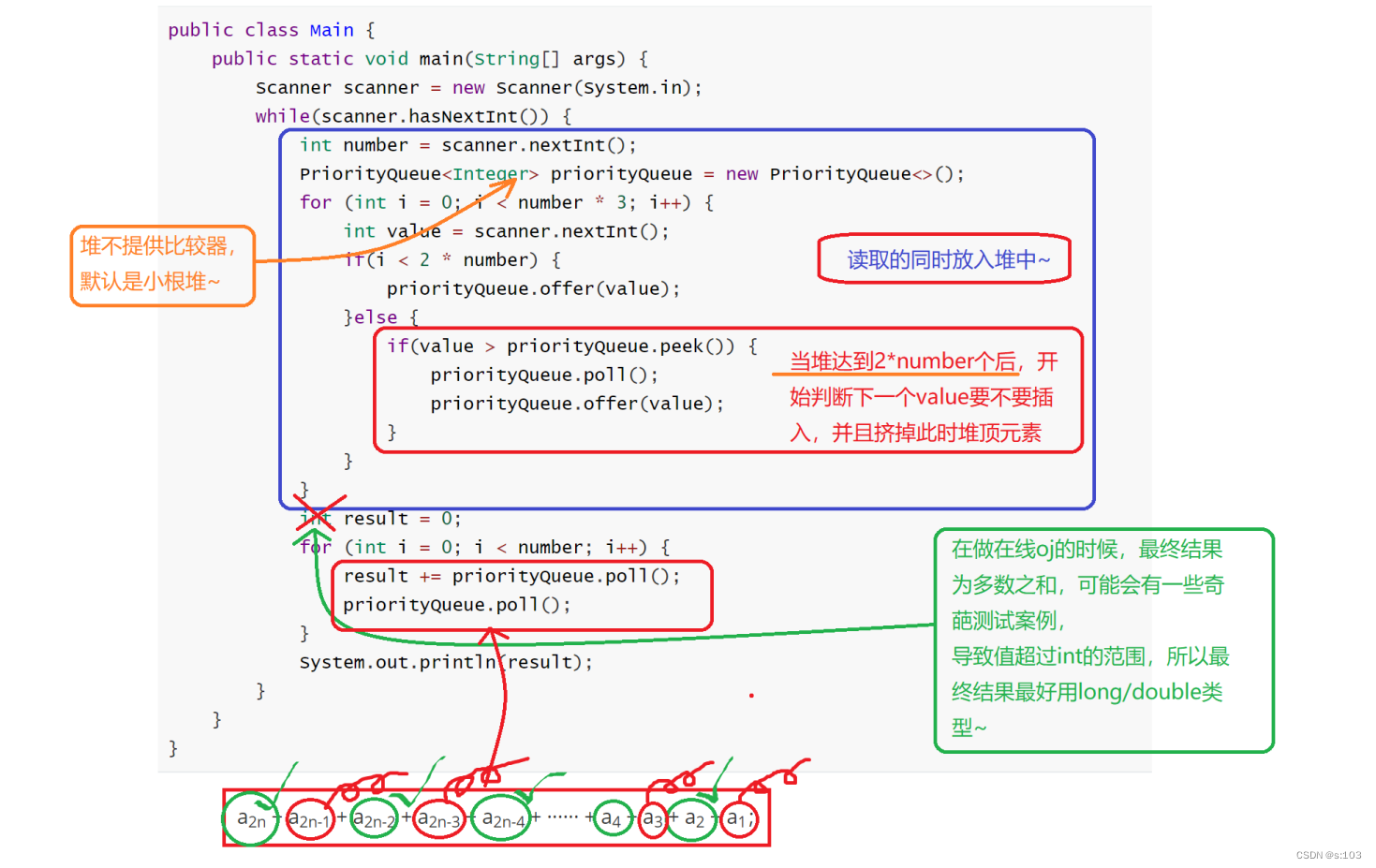
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);while(scanner.hasNextInt()) {int number = scanner.nextInt();PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();for (int i = 0; i < number * 3; i++) {int value = scanner.nextInt();if(i < 2 * number) {priorityQueue.offer(value);}else {if(value > priorityQueue.peek()) {priorityQueue.poll();priorityQueue.offer(value);}}}long result = 0;for (int i = 0; i < number; i++) {result += priorityQueue.poll();priorityQueue.poll();}System.out.println(result);}}
}
- 解析:
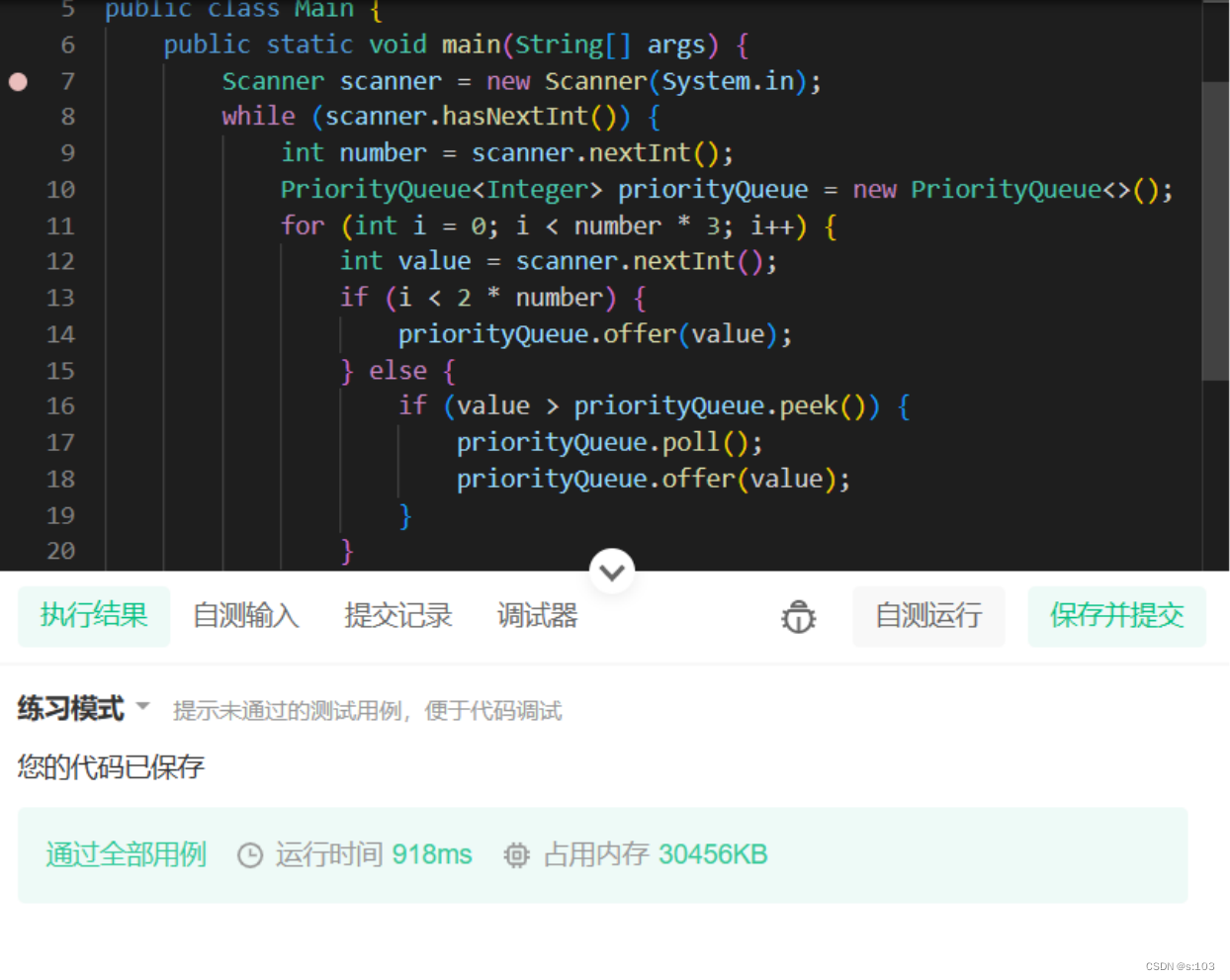
1. 3. 测试
相关文章:

48天强训 Day1 JavaOj
48天强训 & Day1 & JavaOj 1. 编程题1 - 组队竞赛 组队竞赛_牛客笔试题_牛客网 (nowcoder.com) 1.1 读题 1.2 算法思想基础 我们应该尽量的让每一个队伍的中间值都最大化~我们应该尽量的让每一个队伍的最小值都足够小~前33%的不应该都作为每个队伍的最大值~ 接下来…...

崩溃的一瞬间
——我可以忍受黑暗,除非我从未见过光明 原来,人真的会崩溃,如果不是昨夜的眼泪,我到现在还不知道人为什么会在一瞬间崩溃。 刚和认识不久的女孩子聊完天准备入睡。忽然想到自己可能过几个月就要离开这座待了仅一年多的城市…...

13回归网络:HTTP/2是怎样的网络协议?
本篇文章我们先放下实践,回归网络,深入gRPC底层的HTTP/2协议,去探究一下框架底层网络协议的原理,提升对高性能网络协议的认知,相信读完这篇文章以后,我们就可以了解HTTP/2有哪些优势,为什么gRPC要使用HTTP/2作为底层的传输协议。 在众多研究HTTP/2的博客和资料中,最具…...

CSS学习笔记——基础选择器,字体属性,文本属性,三种样式表
文章目录基础选择器标签选择器类选择器多类名使用方式id选择器通配符选择器字体属性字体系列字体字号字体粗细文字样式复合属性文本属性文本颜色对齐文本装饰文本文本缩进行间距CSS的三种样式表行内样式表(行内式)内部样式表(嵌入式ÿ…...
第十四届蓝桥杯三月真题刷题训练——第 16 天
目录 第 1 题:英文字母 问题描述 输入格式 输出格式 样例输入 1 样例输出 1 样例输入 2 样例输出 2 评测用例规模与约定 运行限制 代码: 第 2 题:单词分析 题目描述 输入描述 输出描述 输入输出样例 运行限制 数组代码&…...
鸟哥的Linux私房菜 Shell脚本
第十二章、学习 Shell Scripts https://linux.vbird.org/linux_basic/centos7/0340bashshell-scripts.php 12.2 简单的 shell script 练习 #!/bin/bash# Program: # User inputs his first name and last name. Program shows his full name.read -p "Please in…...

FPGA基于RIFFA实现PCIE采集ov5640图像传输,提供工程源码和QT上位机
目录1、前言2、RIFFA理论基础3、设计思路和架构4、vivado工程详解5、上板调试验证并演示6、福利:工程代码的获取1、前言 PCIE是目前速率很高的外部板卡与CPU通信的方案之一,广泛应用于电脑主板与外部板卡的通讯,PCIE协议极其复杂,…...

week13周报
一.动态规划走楼梯2难点:不能连续走三次两级台阶如何表示思路:可以用二维数组f[i][j],i表示当前台阶数,j表示已经连续走了j次二级台阶了转移方程:f[i2][j1]f[i2][j1]f[i][j] 当j!2时,我们可以选择走二级台阶…...

离散选择模型中的分散系数theta到底该放在哪里呢?
前言 \quad~~一直都在想为啥子离散选择模型中分散系数以分母形式出现而在路径选择公式中以系数形式出现呢?看着公式想了想,现在想出了一个似乎感觉应该差不多很合理的答案,希望与大家一起探讨。 进入正题 根据随机效用理论,决策…...

【CSAPP】进程 | 上下文切换 | 用户视角下的并发进程
💭 写在前面:本文将学习《深入理解计算机系统》的第六章 - 关于异常控制流和系统级 I/O 的 进程部分。CSAPP 是计算机科学经典教材《Computer Systems: A Programmers Perspective》的缩写,该教材由Randal E. Bryant和David R. OHallaron 合著…...
节流还在用JS吗?CSS也可以实现哦
函数节流是一个我们在项目开发中常用的优化手段,可以有效避免函数过于频繁的执行。一般函数节流用在scroll页面滚动,鼠标移动等。 为什么需要节流呢,因为触发一次事件就会执行一次事件,这样就形成了大量操作dom,会出现卡顿的情况…...

带你看看 TypeScript 5.0 的新特性
一、写在前面 TypeScript 5.0 已经于 2023 年 3 月 16 日发布了,带来了许多新功能,同时也在性能方面进行了优化,下面让我们来一起看看新版 TypeScript 中比较有重要的变化吧。 二、新特性 2-1、速度、包体积优化 首先是新版本性能的提升&…...

C语言预处理条件语句的 与或运算
C语言预处理条件语句的 与或运算 1.#ifdef 与或运算 #ifdef (MIN) && (MAX) ----------------------------错误使用 #if defined(MIN) && defined(MAX) ---------------- 正确使用 #ifdef (MIN) || (MAX) -----------------------------错误使用 …...
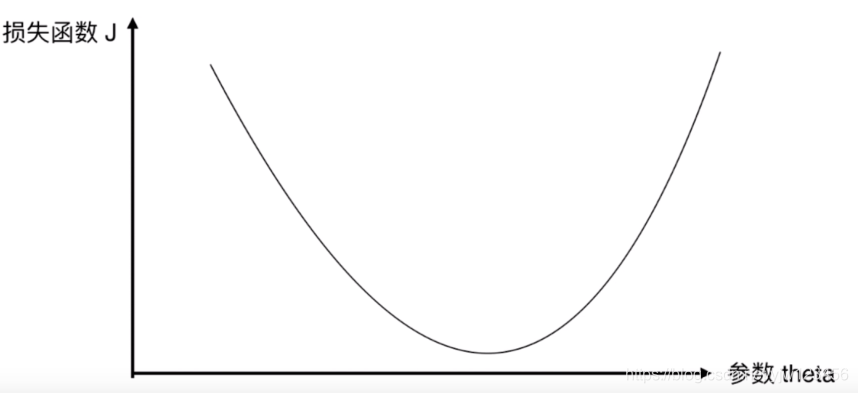
从零实现深度学习框架——学习率调整策略介绍
引言 本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。 要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不使用外部完备的框架前提下,实现我…...
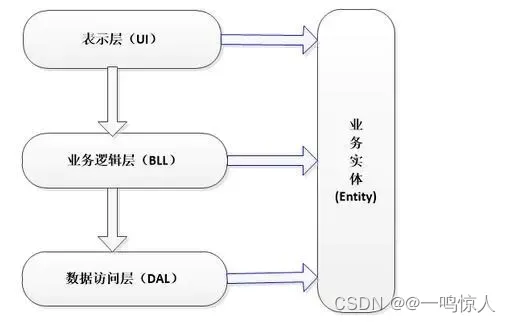
系统架构:经典三层架构
引言 经典三层架构是分层架构中最原始最典型的分层模式,其他分层架构都是其变种或扩展,例如阿里的四层架构模式和DDD领域驱动模型。阿里的 四层架构模型在三层基础上增加了 Manager 层,从而形成变种四层模型;DDD架构则在顶层用户…...
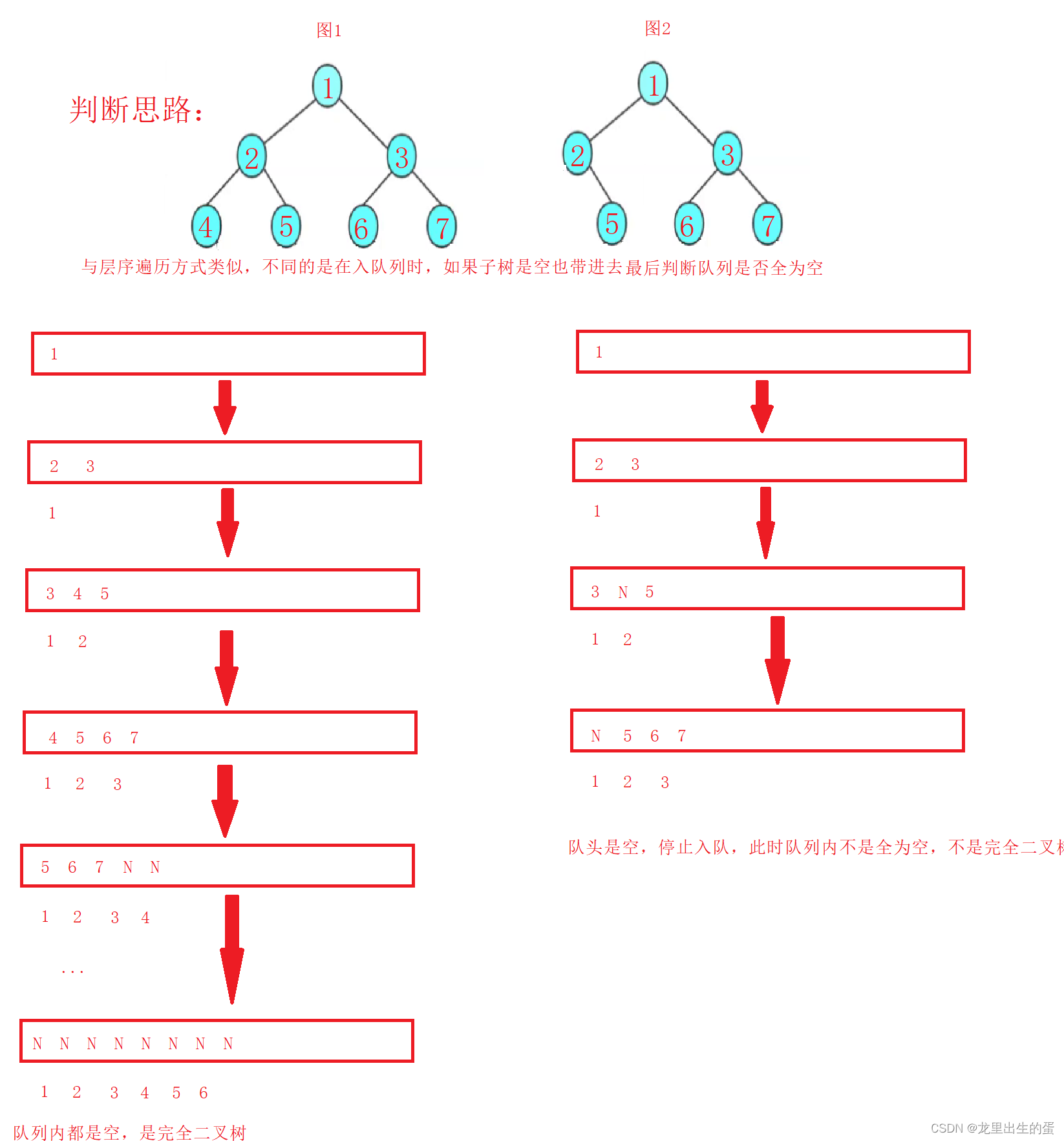
数据结构--二叉树
目录1.树概念及结构1.1数的概念1.2数的表示2.二叉树概念及结构2.1二叉树的概念2.2数据结构中的二叉树2.3特殊的二叉树2.4二叉树的存储结构2.4.1顺序存储2.4.2链式存储2.5二叉树的性质3.堆的概念及结构3.1堆的实现3.1.1堆的创建3.1.2堆的插入3.1.3堆顶的删除3.1.4堆的代码实现3.…...

Keil5安装和使用小记
随着keil版本的更新,一些使用问题一随之产生。本文针对安装目前最新版本keil软件和使用问题做一些总结。 目录1 Keil5下载&安装1.1 官网下载链接1.2 软件安装1.2.1 安装说明1.2.2 关于 51 和 ARM 共存的问题1.3 软件破解2 pack包安装 & 破解2.1 下载2.2 安装…...
多机器人集群网络通信协议分析
本文讨论的是多机器人网络通信各层的情况和协议。 每个机器人连接一个数据传输通信模块(以下简称为数传,也泛指市面上的图传或图数一体的通信模块),数传之间进行组网来传递信息。 根据ISO的划分,网络通信的OSI模型分…...

【PyTorch】手把手带你快速搭建PyTorch神经网络
手把手带你快速搭建PyTorch神经网络1. 定义一个Class2. 使用上面定义的Class3. 执行正向传播过程4. 总结顺序相关资料话不多说,直接上代码1. 定义一个Class 如果要做一个神经网络模型,首先要定义一个Class,继承nn.Module,也就是i…...

【完整代码】用HTML/CSS制作一个美观的个人简介网页
【完整代码】用HTML/CSS制作一个美观的个人简介网页整体结构完整代码用HTML/CSS制作一个美观的个人简介网页——学习周记1HELLO!大家好,由于《用HTML/CSS制作一个美观的个人简介网页》这篇笔记有幸被很多伙伴关注,于是特意去找了之前写的完整…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...

安全领域新突破:可视化让隐患无处遁形
在安全领域,隐患就像暗处的 “幽灵”,随时可能引发严重事故。传统安全排查手段,常常难以将它们一网打尽。你是否好奇,究竟是什么神奇力量,能让这些潜藏的隐患无所遁形?没错,就是可视化技术。它如…...

开源项目实战学习之YOLO11:12.6 ultralytics-models-tiny_encoder.py
👉 欢迎关注,了解更多精彩内容 👉 欢迎关注,了解更多精彩内容 👉 欢迎关注,了解更多精彩内容 ultralytics-models-sam 1.sam-modules-tiny_encoder.py2.数据处理流程3.代码架构图(类层次与依赖)blocks.py: 定义模型中的各种模块结构 ,如卷积块、残差块等基础构建…...
