二叉搜索树:AVL平衡
文章目录
- 一、 二叉搜索树
- 1.1 概念
- 1.2 操作
- 1.3 代码实现
- 二、二叉搜索树的应用
- K模型和KV模型
- 三、二叉搜索树的性能分析
- 四、AVL树
- 4.1 AVL树的概念
- 4.2 AVL树的实现原理
- 4.3 旋转
- 4.4 AVL树最终代码
一、 二叉搜索树
1.1 概念
二叉搜索树( Binary Search Tree,BST )是一种特殊的二叉树,它可以是空树,也可以是满足以下性质的一颗二叉树:
- 若左子树不为空,左子树中所有节点的键值都小于根节点的值。
- 若右子树不为空,右子树中所有节点的键值都大于根节点的值。
- 左右子树也分别为二叉搜索树。
因此,二叉搜索树的中序遍历结果是一个有序序列。这个特性使得二叉搜索树在搜索、插入和删除操作时具有高效性能。
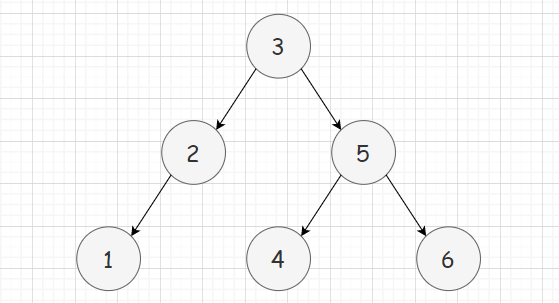
📝二叉搜索树的结构示意图
1.2 操作
⭕ 对如下二叉搜索树进行操作
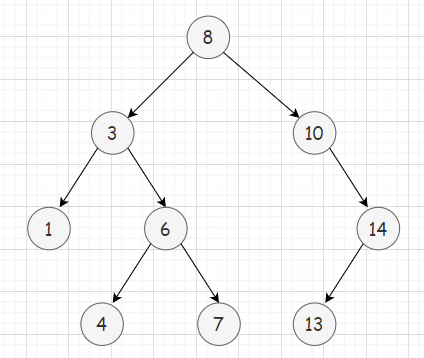
- 查询
🔎假设要查询key值是否存在于二叉树中
- 从根节点开始,key比当前节点的键值大,则往右继续找;key比当前节点的键值小,则往左继续找。
- 若当前节点为空时还没找到,则key值不存在。
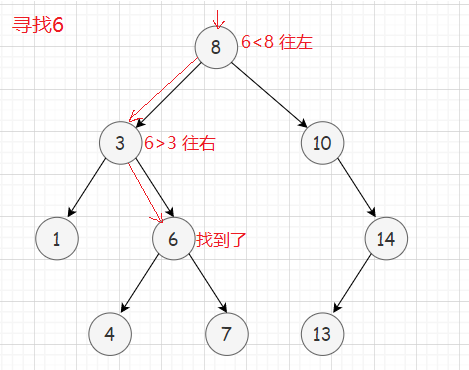
- 插入
1️⃣若树为空,则直接新增节点,作为该树的根节点
2️⃣若树不为空,则按二叉搜索树查询规则找到插入位置,再建立与父节点的链接关系。
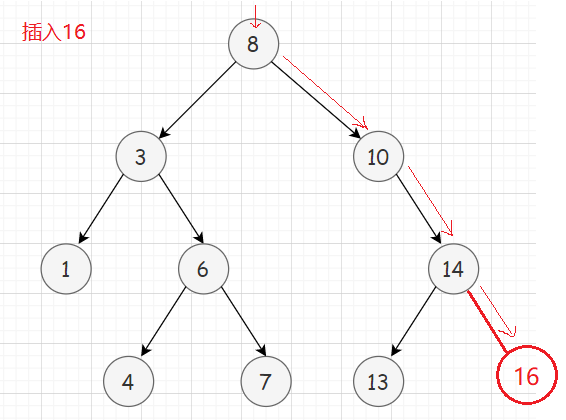
- 删除
二叉搜索树的删除某个节点后,要想继续保持二叉搜索树的特性,需要进行一些调整。这里分三种情况。
假设将要删除node节点
1️⃣ 若node没有子树,即node为叶子节点,那么直接删除即可。
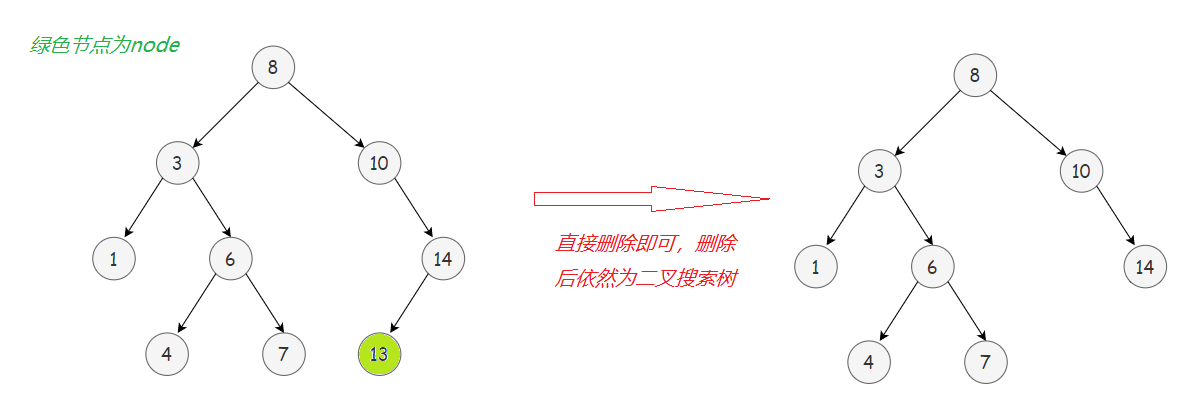
2️⃣ 若node左右子树有一边为空一边非空,则需“托孤”,即把非空一边的子树托付给node父节点。
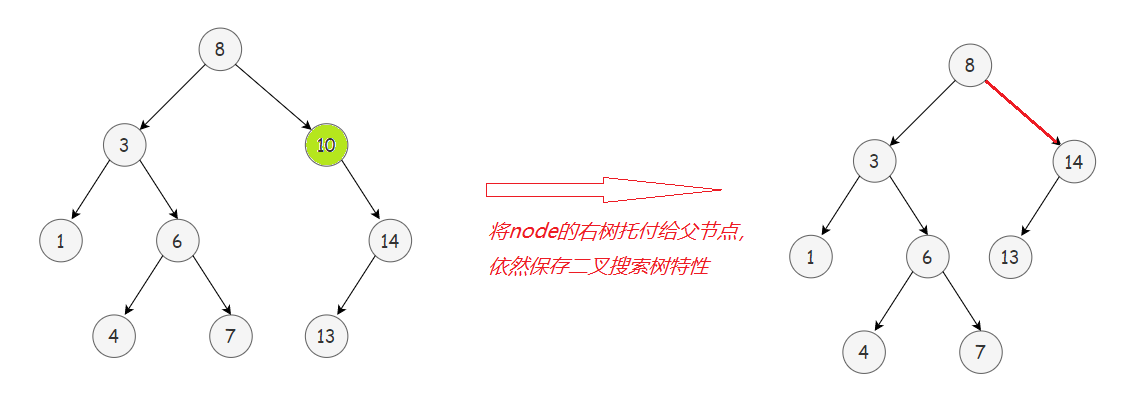
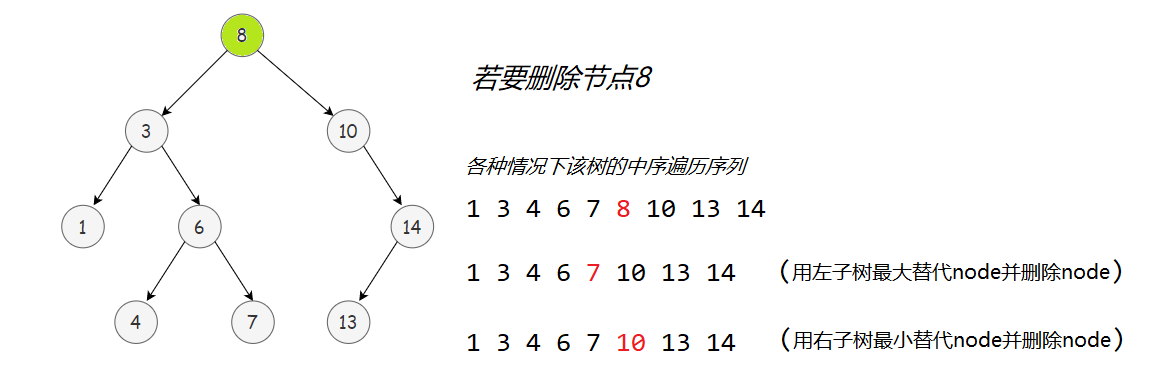
3️⃣ 若node左右子树都存在,则需在左子树中找到最大节点(或在右子树中找到最小节点)来替代node,然后在左子树(或右子树)中删除node。
观察二叉搜索树的中序遍历序列,可见进行上述操作后,中序遍历序列依然有序,二叉搜索树保持其特性。
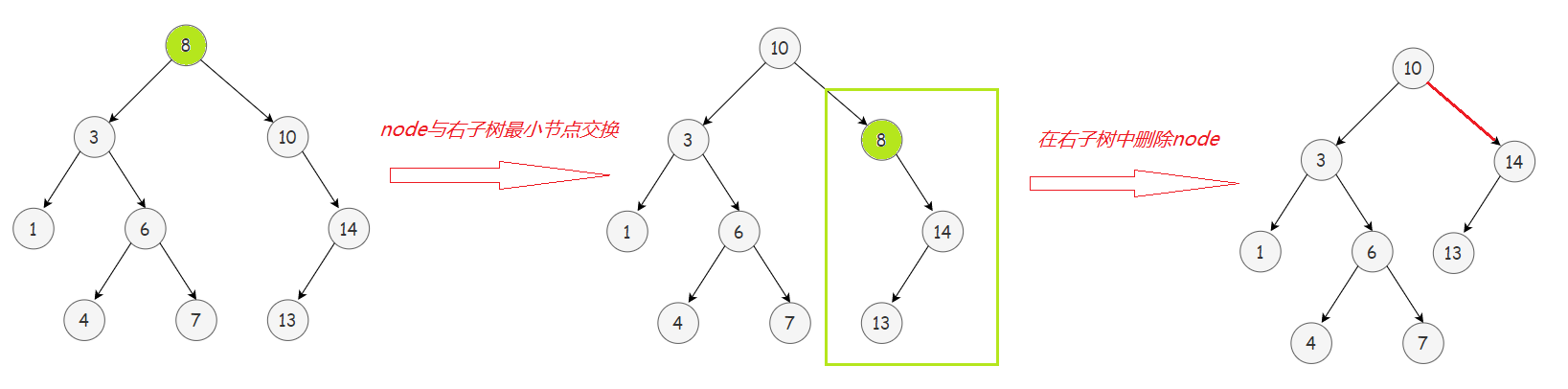
💡替换node后,在左子树(或右子树)中删除node,这样做还有一个好处:
因为node是与左子树中最大节点(或右子树中最小节点)替换后,所以替换后的node一定没有右子树(或左子树),因此在这种情况下删除node,必然是删除节点的1️⃣或2️⃣情况,避免了重复3️⃣情况删除而进入死循环。
1.3 代码实现
#include <iostream>
#include <algorithm>
using namespace std;// 二叉搜索树的节点
template <class K>
struct BSTreeNode
{typedef BSTreeNode<K> Self;Self* _pleft;Self* _pright;K _key;BSTreeNode(const K& key):_key(key),_pleft(nullptr),_pright(nullptr){}
};// 二叉搜索树
template <class K>
class BSTree
{typedef BSTreeNode<K> Node;typedef BSTreeNode<K>* pNode;public:// constructorBSTree():_root(nullptr){}// destructor~BSTree(){_destroy(_root);}// 中序遍历void Inorder(){_inorder(_root);cout << endl;}// 插入bool Insert(const K& key){// 空树if(_root == nullptr){_root = new Node(key);return true;}// 不为空树,要先找到插入位置else{pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else{return false;}}cur = new Node(key);if (cur->_key > parent->_key)parent->_pright = cur;elseparent->_pleft = cur;return true;}}// 删除void Erase(const K& key){_erase(_root, key);}private:pNode _root;void _inorder(pNode root){if (root == nullptr)return;_inorder(root->_pleft);cout << root->_key << " ";_inorder(root->_pright);}void _destroy(pNode root){if (root == nullptr)return;_destroy(root->_pleft);_destroy(root->_pright);delete root;}bool _erase(pNode& root, const K& key){// 先找到key值的节点pNode cur = root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else // 相等,找到了break;}if (cur == nullptr) // 查无key值节点return false;// 1. cur左右至少有一个空(1️⃣、2️⃣情况)if (cur->_pleft == nullptr || cur->_pright == nullptr){pNode child = cur->_pleft;if (child == nullptr)child = cur->_pright;// cur为根if (cur == root){root = child;}// cur不为根else{if (cur == parent->_pleft){parent->_pleft = child;}else{parent->_pright = child;}}delete cur;cur = nullptr;}// 2. cur左右都非空(3️⃣情况)else{//(1)找到右边最小(也可以是左边最大,通常小的离根较近,我们选用右边最小)的节点代替curpNode minRight = cur->_pright;while (minRight->_pleft){minRight = minRight->_pleft;}swap(cur->_key, minRight->_key);//(2)转换为在cur的右子树删除minRight节点_erase(cur->_pright, minRight->_key); // 此时一定是1️⃣或2️⃣情况}return true;}
};
💡 _erase函数root参数设为引用的妙处在cur为根时,体现为以下两种情况相同处理
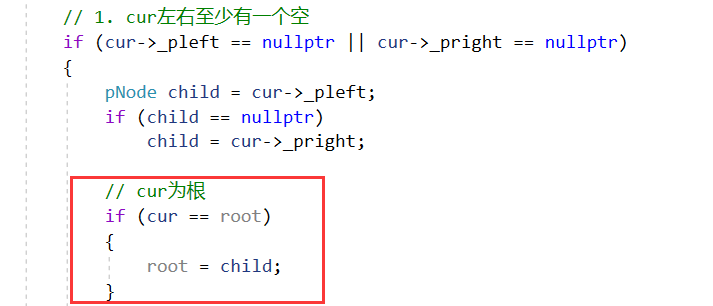
1. _erase(_root, key);
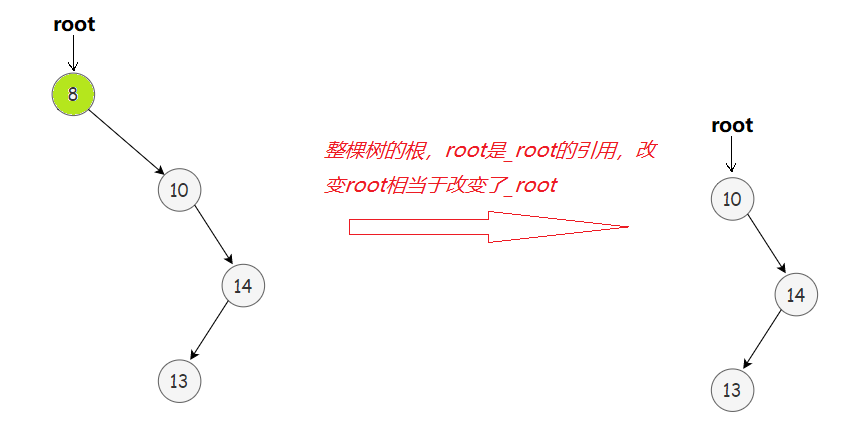
2. _erase(cur->_pright(或cur->_pleft), minRight->_key);
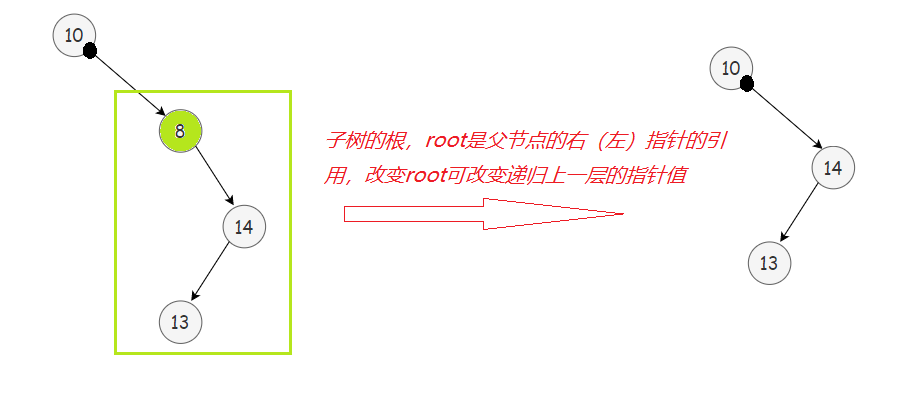
二、二叉搜索树的应用
K模型和KV模型
- K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到
的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下: 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树,在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
- KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方
式在现实生活中非常常见
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英 文单词与其对应的中文
<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
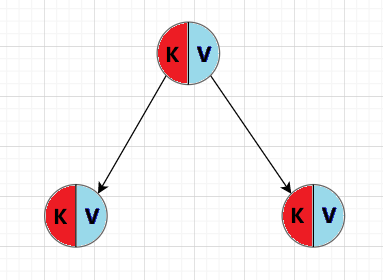
💬KV模型的代码实现:
// KV型
template <class K, class V>
struct BSTreeNode
{typedef BSTreeNode<K, V> Self;Self* _pleft;Self* _pright;K _key;V _val;BSTreeNode(const K& key, const V& val): _key(key), _val(val), _pleft(nullptr), _pright(nullptr){}
};template <class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;typedef BSTreeNode<K, V>* pNode;public://constructorBSTree():_root(nullptr){}//destructor~BSTree(){_destroy(_root);}void Inorder(){_inorder(_root);cout << endl;}bool Insert(const K& key,const V& val){// 空树if (_root == nullptr){_root = new Node(key, val);return true;}// 不为空树,要先找到插入位置else{pNode cur = _root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else{return false;}}cur = new Node(key, val);if (cur->_key > parent->_key)parent->_pright = cur;elseparent->_pleft = cur;return true;}}void Erase(const K& key){_erase(_root, key);}pNode Find(const K& key){pNode cur = _root;while (cur){if (key > cur->_key){cur = cur->_pright;}else if (key < cur->_key){cur = cur->_pleft;}else{return cur;}}return nullptr;}
private:pNode _root;void _inorder(pNode root){if (root == nullptr)return;_inorder(root->_pleft);cout << root->_key << ":" << root->_val << endl;_inorder(root->_pright);}void _destroy(pNode root){if (root == nullptr)return;_destroy(root->_pleft);_destroy(root->_pright);delete root;}bool _erase(pNode& root, const K& key){// 先找到key值的节点pNode cur = root;pNode parent = nullptr;while (cur){if (key > cur->_key){parent = cur;cur = cur->_pright;}else if (key < cur->_key){parent = cur;cur = cur->_pleft;}else // 相等,找到了break; }if (cur == nullptr) // 查无key值节点return false;// 1. cur左右至少有一个空if (cur->_pleft == nullptr || cur->_pright == nullptr){pNode child = cur->_pleft;if (child == nullptr)child = cur->_pright;// cur为根if (cur == root){root = child;}// cur不为根else{// cur左右都为空if (child == nullptr){if (parent->_pleft->_key == cur->_key){parent->_pleft = nullptr;}else{parent->_pright = nullptr;}}// cur左右只有一个为空,不为空的为childelse{if (child->_key < parent->_key){parent->_pleft = child;}else{parent->_pright = child;}}if (cur == parent->_pleft){parent->_pleft = child;}else{parent->_pright = child;}}delete cur;cur = nullptr;}//2. cur左右都非空else{//找到右边最小的节点代替curpNode minRight = cur->_pright;while (minRight->_pleft){minRight = minRight->_pleft;}swap(cur->_key, minRight->_key);//转换为在cur的右子树删除minRight节点_erase(cur->_pright, minRight->_key);}return true;}
};
三、二叉搜索树的性能分析
💭 二叉搜索树的插入、删除等操作,时间大部分都花费在查找节点上了。因此分析二叉搜索树的性能,主要看查找的性能。
假设二叉树有N个节点
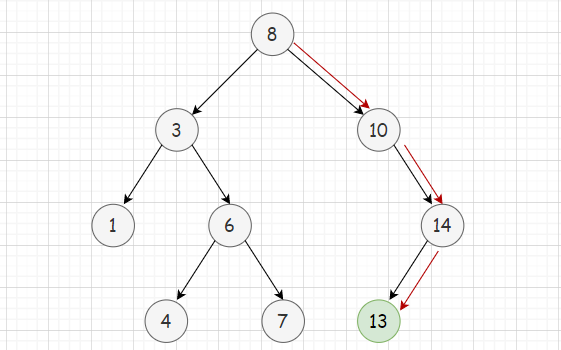
如图是最优情况下的查找,该二叉搜索树接近完全二叉树,此时查找节点的时间复杂度是O(logN)
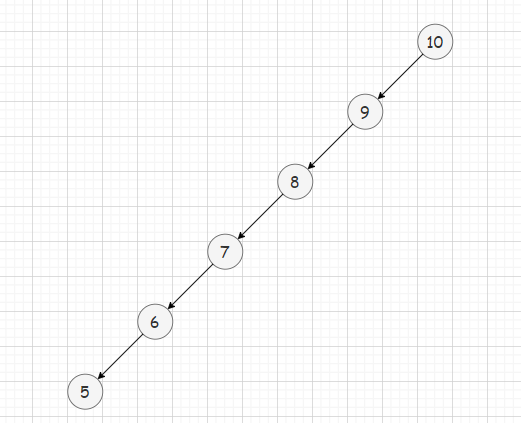
*但也有上图所示的极端情况,有序插入节点后,二叉搜索树退化为单支,这种情况是最差情况,查找节点的时间复杂度为O(N)
💭 二叉搜索树退化为接近单支树时,其效率和性能就失去了。为了解决这个问题,使二叉搜索树始终保持最优情况,我们可以将二叉搜索树改造为AVL树和红黑树。下文分析AVL树。
四、AVL树
4.1 AVL树的概念
💭二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
能满足这种特性的树称为AVL树
⭕一颗AVL树可以是一棵空树,也可以是有以下性质的一棵二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度差(简称平衡因子)的绝对值不超过1
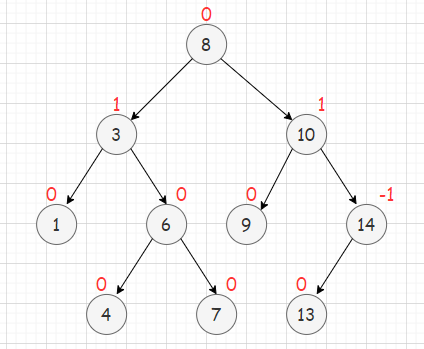
AVL树是一棵高度平衡的树。一棵n个节点的AVL树的高度为O(logn),查找的时间复杂度为O(logn)。
⭕定义
// AVL树的节点
template <class T>
struct AVLTreeNode
{AVLTreeNode(const T& val):_val(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}AVLTreeNode* _left; // 左指针AVLTreeNode* _right; // 右指针AVLTreeNode* _parent; // 双亲指针T _val;int _bf;// 平衡因子
};
// AVL树
template <class T>
class AVLTree
{typedef AVLTreeNode<T> node;typedef AVLTreeNode<T>* ptr;public:AVLTree():_root(nullptr){}bool insert(const T& val);private:ptr _root;
};
4.2 AVL树的实现原理
💭AVL树的原理主要体现在插入时要通过对节点的调节,以保证每个节点的左右子树高度差绝对值不超过1(即平衡因子不超过1)。插入后,分为以下三种情况。
默认平衡因子 = 右子树高度 - 左子树高度
- 插入后,父节点的平衡因子变为0
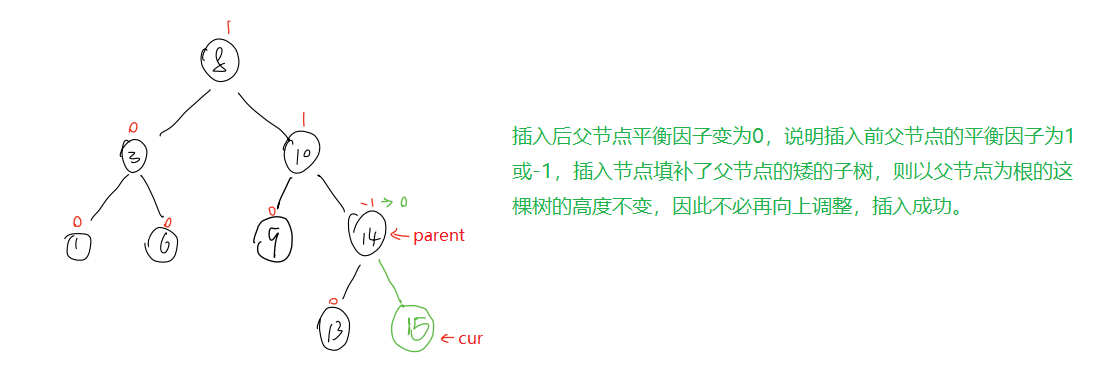
- 插入后,父节点的平衡因子变为1或-1

- 插入后,父节点的平衡因子变为2或-2
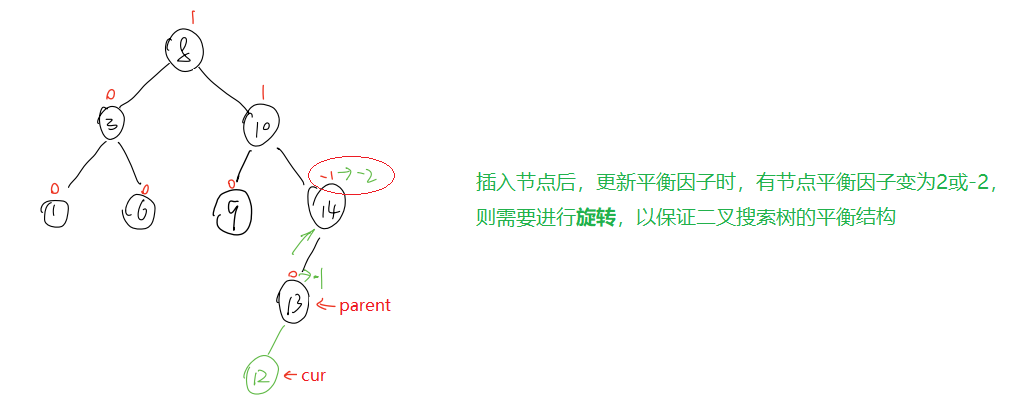
那么这里的旋转到底是怎么一回事?见后文详细分析。
📃 先搭建AVL树insert插入函数定义的大致框架
bool insert(const T& val){// 先按二叉搜索树规则,找到插入位置ptr cur = _root;ptr parent = nullptr;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{// 相同元素不能插入return false;}}// 创建新节点并插入cur = new node(val);// 若根为空,直接把cur作根if (_root == nullptr){_root = cur;return true;}else{if (cur->_val < parent->_val){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}}// 更新平衡因子while (parent){if (cur == parent->_left){(parent->_bf)--;}else{(parent->_bf)++;}// 1.parent的_bf更新后为0if (parent->_bf == 0){// 插入成功break;}// 2.parent的_bf更新后为1或-1,此时需要继续向上更新平衡因子else if (parent->_bf == 1 || parent->_bf == -1){//持续往上更新cur = parent;parent = parent->_parent;}// 3.parent的_bf更新后为2或-2,此时需要旋转,旋转后以parent为根的子树为平衡二叉树,不需要在继续向上更新平衡因子else if (parent->_bf == 2 || parent->_bf == -2){// 旋转...break;}}return true;}
4.3 旋转
🔎如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。这种调整称之为旋转。根据节点插入位置的不同,AVL树的旋转分为四种:
- 左左 —— 右单旋
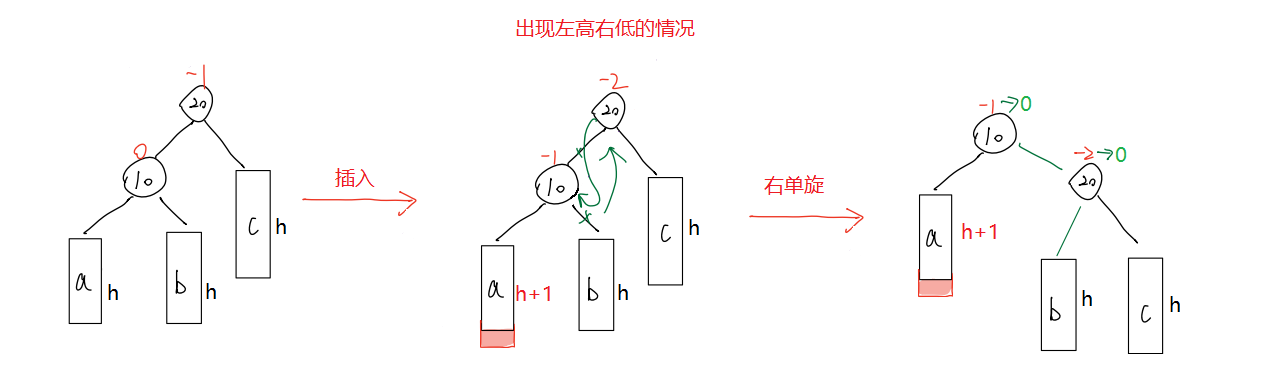
为什么能这样旋转?
- b在20的左子树,肯定比20小,故能作20的左子树
- 20和b都人于10,故以20为根的子树能作10的右子树
💬 代码实现
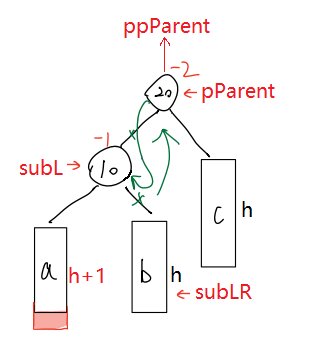
// 左左--右单旋void RotateR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;ptr ppParent = pParent->_parent;//建立新的链接关系//1.pParent(父)和subLR(子)pParent->_left = subLR;if (subLR)subLR->_parent = pParent;//2.subL(父)和pParent(子)subL->_right = pParent;pParent->_parent = subL;//3.ppParent(父)和subL(子)if (pParent == _root){_root = subL;}else{if (ppParent->_left == pParent){ppParent->_left = subL;}else{ppParent->_right = subL;}}subL->_parent = ppParent;//4.更新平衡因子subL->_bf = pParent->_bf = 0;}
- 右右 —— 左单旋
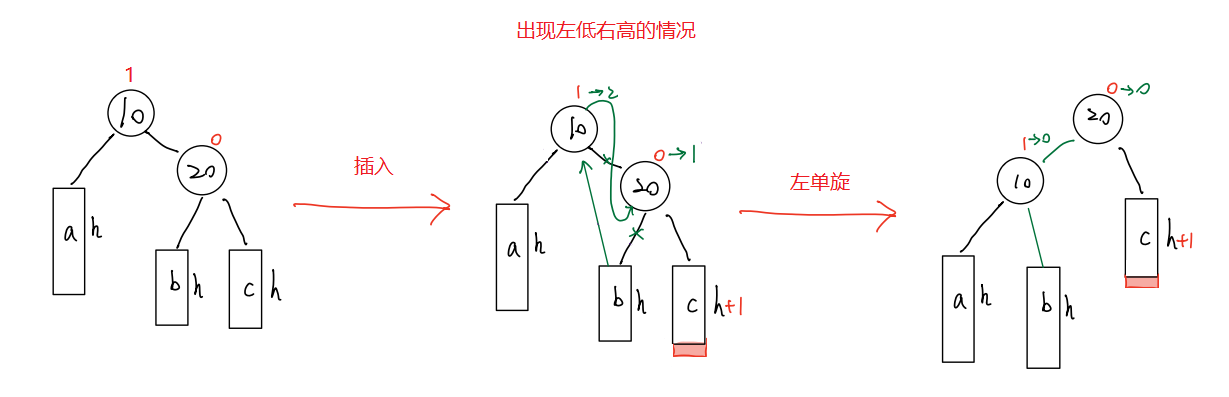
💬 代码实现
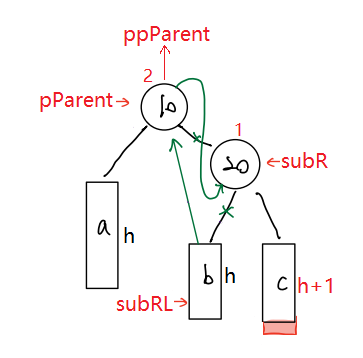
// 右右--左单旋void RotateL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;ptr ppParent = pParent->_parent;pParent->_right = subRL;if (subRL)subRL->_parent = pParent;subR->_left = pParent;pParent->_parent = subR;if (pParent == _root){_root = subR;}else{// 是否可以用函数参数引用 ptr& pParent 优化?//if (subR->_val < ppParent->_val)if (ppParent->_left == pParent){ppParent->_left = subR;}else{ppParent->_right = subR;}}subR->_parent = ppParent;subR->_bf = pParent->_bf = 0;}
- 左右 —— 左右双旋
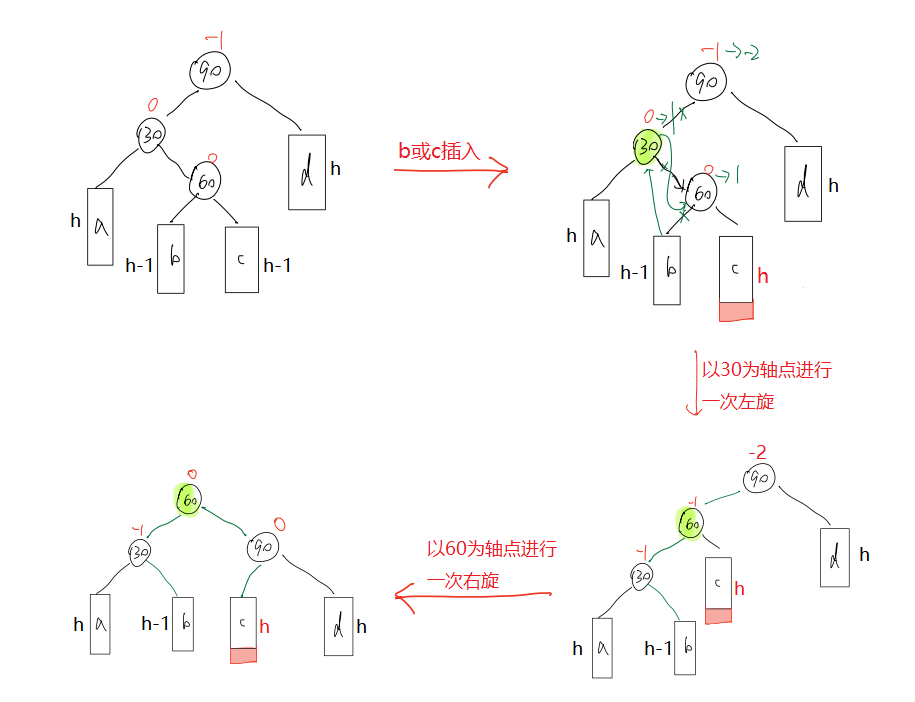
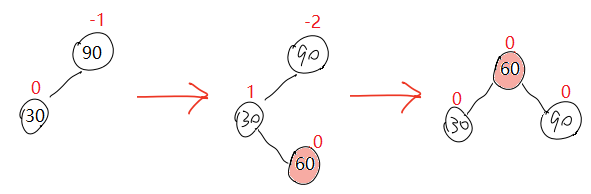
🔎我们可以复用RotateL(左单旋)和RotateR(右单旋)来实现右左双旋,但需要注意的是,这两个函数会把平衡因子直接更新为0,但是观察右左双旋的过程图,发现结果所更新节点的平衡因子不全为0。因此,右左双旋要自己更新平衡因子,不能依赖于RotateL和RotateR。
- 当在c子树插入新节点时,旋转后的结果
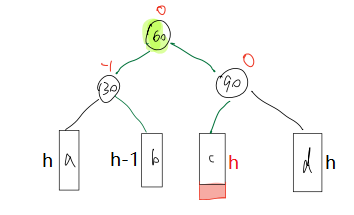
-
当在b子树插入新节点时,旋转后的结果
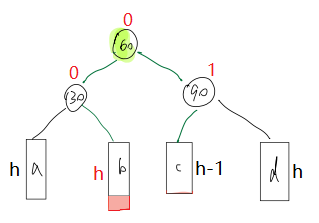
-
特殊情况,当h==0时,30的右子树为空,60就是新插入节点。最终平衡因子全为0。
💬 代码实现
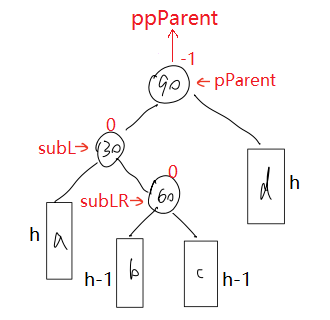
🔎通过上两张图可以发现,当在c子树插入时,最终subL指向节点的平衡因子为-1,其他两个为0;当在b子树插入时,最终pParent指向节点的平衡因子为1,其他两个为0。因此,判断在哪颗树插入时决定最终如何更新平衡因子的关键,而插入后且调整前的subLR的平衡因子就可以判断。插入后且调整前,若subLR的平衡因子为1,则是在c子树插入;若subLR的平衡因子为-1,则是在b子树插入。还有h==0的特殊情况,此时subLR的平衡因子为0,作特殊处理。
void RotateLR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;int bf = subLR->_bf; // 保存插入后调整前subLR的平衡因子// 两次旋转RotateL(subL);RotateR(pParent);// 更新平衡因子if (bf == 1){subLR->_bf = 0;subL->_bf = -1;pParent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 1;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 0;}else{assert(false);}}
- 右左 —— 右左双旋
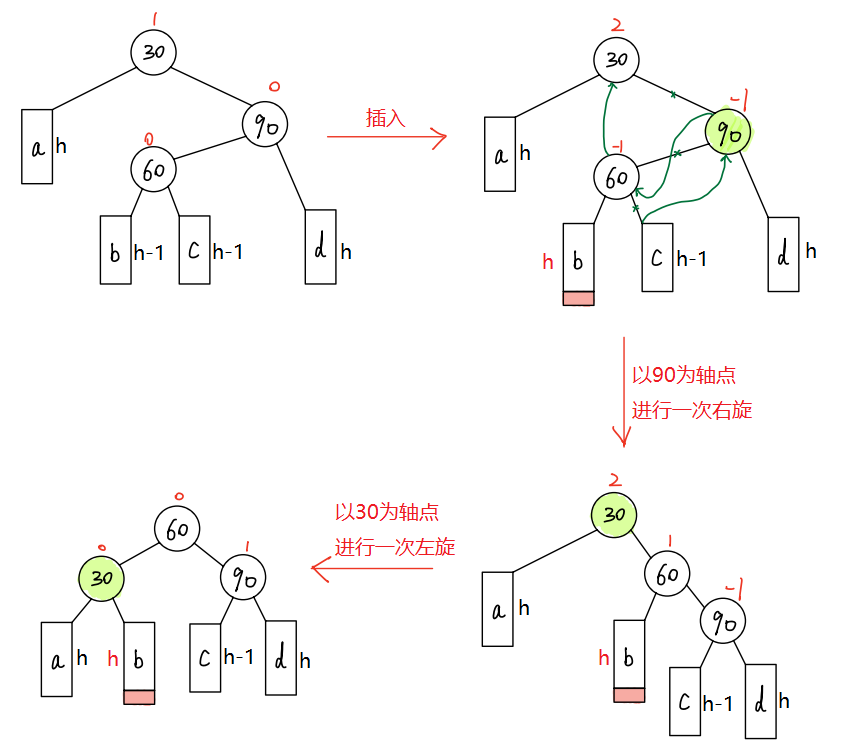
- 当在c子树插入新节点时,旋转后的结果
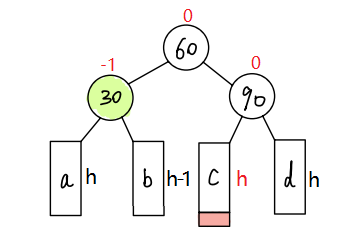
- 当在b子树插入新节点时,旋转后的结果
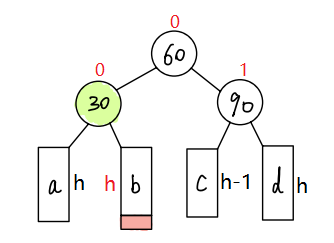
💬代码实现
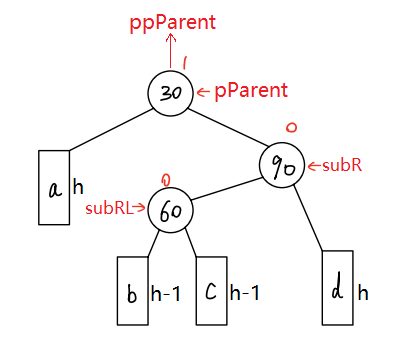
void RotateRL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(pParent);if (bf == 1){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;pParent->_bf = 0;}else if (bf == 0){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = 0;}else{assert(false);}}
4.4 AVL树最终代码
// AVL树的节点
template <class T>
struct AVLTreeNode
{AVLTreeNode(const T& val):_val(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;T _val;int _bf;// 平衡因子
};// AVL树
template <class T>
class AVLTree
{typedef AVLTreeNode<T> node;typedef AVLTreeNode<T>* ptr;public:// 构造函数AVLTree():_root(nullptr){}// 析构函数~AVLTree(){destroy(_root);}// 中序遍历void InOrder(){_inorder(_root);}// 插入新节点bool insert(const T& val){// 先按二叉搜索树规则,找到插入位置ptr cur = _root;ptr parent = nullptr;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{// 相同元素不能插入return false;}}// 创建新节点并插入cur = new node(val);if (_root == nullptr){_root = cur;return true;}else{if (cur->_val < parent->_val){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}}// 更新平衡因子while (parent){if (cur == parent->_left){(parent->_bf)--;}else{(parent->_bf)++;}// 1.parent的_bf更新后为0if (parent->_bf == 0){// 插入成功break;}// 2.parent的_bf更新后为1或-1,此时需要继续向上更新平衡因子else if (parent->_bf == 1 || parent->_bf == -1){//持续往上更新cur = parent;parent = parent->_parent;}// 3.parent的_bf更新后为2或-2,此时需要旋转,旋转后以parent为根的子树为平衡二叉树,不需要在继续向上更新平衡因子else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}}return true;}bool IsBalance() {return is_balance(_root);}int Height(){return get_height(_root);}private:// 检查该树是否平衡bool is_balance(ptr root){if (root == nullptr)return true;int leftHeight = get_height(root->_left);int rightHeight = get_height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_val << "平衡因子异常" << endl;}return (abs(rightHeight - leftHeight) == 1 || rightHeight == leftHeight)&& is_balance(root->_left)&& is_balance(root->_right);}// 获取以root为根的子树的高度int get_height(ptr root){if (root == nullptr)return 0;return 1 + max(get_height(root->_left), get_height(root->_right));}// 析构函数的子函数void destroy(ptr root){if (root == nullptr)return;destroy(root->_left);destroy(root->_right);delete root;}void _inorder(ptr root){if (root == nullptr)return;_inorder(root->_left);cout << root->_val << " ";_inorder(root->_right);}// 左左--右单旋void RotateR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;ptr ppParent = pParent->_parent;//1.pParent(父)和subLR(子)pParent->_left = subLR;if (subLR)subLR->_parent = pParent;//2.subL(父)和pParent(子)subL->_right = pParent;pParent->_parent = subL;//3.ppParent(父)和subL(子)if (pParent == _root){_root = subL;}else{// 是否可以用函数参数引用 ptr& pParent 优化?if (ppParent->_left == pParent){ppParent->_left = subL;}else{ppParent->_right = subL;}}subL->_parent = ppParent;//4.更新平衡因子subL->_bf = pParent->_bf = 0;}// 右右--左单旋void RotateL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;ptr ppParent = pParent->_parent;pParent->_right = subRL;if (subRL)subRL->_parent = pParent;subR->_left = pParent;pParent->_parent = subR;if (pParent == _root){_root = subR;}else{// 是否可以用函数参数引用 ptr& pParent 优化?//if (subR->_val < ppParent->_val)if (ppParent->_left == pParent){ppParent->_left = subR;}else{ppParent->_right = subR;}}subR->_parent = ppParent;subR->_bf = pParent->_bf = 0;}void RotateLR(ptr pParent){ptr subL = pParent->_left;ptr subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(pParent);if (bf == 1){subLR->_bf = 0;subL->_bf = -1;pParent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 1;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 0;}else{assert(false);}}void RotateRL(ptr pParent){ptr subR = pParent->_right;ptr subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(pParent);if (bf == 1){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;pParent->_bf = 0;}else if (bf == 0){subRL->_bf = 0;subR->_bf = 0;pParent->_bf = 0;}else{assert(false);}}ptr _root;
};
完。
相关文章:

二叉搜索树:AVL平衡
文章目录一、 二叉搜索树1.1 概念1.2 操作1.3 代码实现二、二叉搜索树的应用K模型和KV模型三、二叉搜索树的性能分析四、AVL树4.1 AVL树的概念4.2 AVL树的实现原理4.3 旋转4.4 AVL树最终代码一、 二叉搜索树 1.1 概念 二叉搜索树( Binary Search Tree,…...
数据结构和算法(1):数组
目录概述动态数组二维数组局部性原理越界检查概述 定义 在计算机科学中,数组是由一组元素(值或变量)组成的数据结构,每个元素有至少一个索引或键来标识 In computer science, an array is a data structure consisting of a col…...
python+django+vue全家桶鲜花商城售卖系统
重点: (1) 网上花店网站中各模块功能之间的的串联。 (2) 网上花店网站前台与后台的连接与同步。 (3) 鲜花信息管理模块中鲜花的发布、更新与删除。 (4) 订单…...
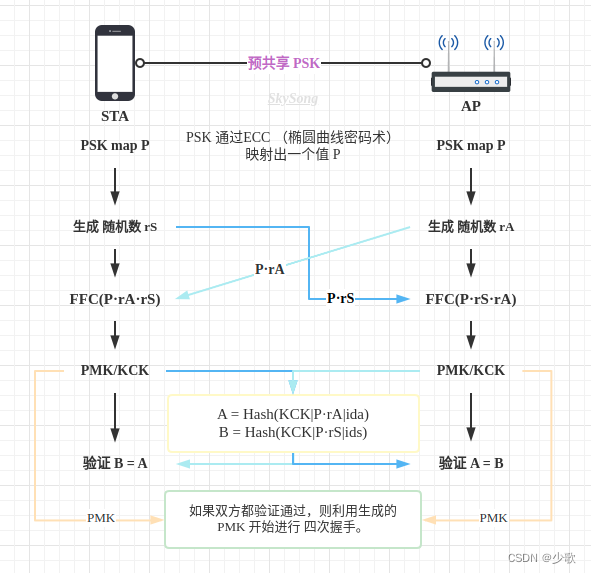
一文带你领略 WPA3-SAE 的 “安全感”
引入 WPA3-SAE也是针对四次握手的协议。 四次握手是 AP (authenticator) 和 (supplicant)进行四次信息交互,生成一个用于加密无线数据的秘钥。 这个过程发生在 WIFI 连接 的 过程。 为了更好的阐述 WPA3-SAE 的作用 …...
Python解题 - CSDN周赛第38期
又来拯救公主了。。。本期四道题还是都考过,而且后面两道问哥在以前写的题解里给出了详细的代码(当然是python版),直接复制粘贴就可以过了——尽管这样显得有失公允,考虑到以后还会出现重复的考题,所以现在…...
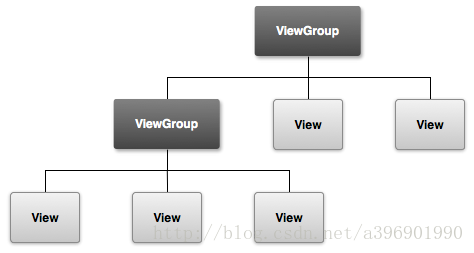
Android绘制——自定义view之onLayout
简介 在自定义view的时候,其实很简单,只需要知道3步骤: 测量——onMeasure():决定View的大小,关于此请阅读《Android自定义控件之onMeasure》布局——onLayout():决定View在ViewGroup中的位置绘制——onD…...

用Qt画一个温度计
示例1 以下是用Qt绘制一个简单的温度计的示例代码: #include <QPainter> #include <QWidget> #include <QApplication> class Thermometer : public QWidget { public:Thermometer(QWidget *parent 0); protected:void paintEvent(QPaintEvent …...
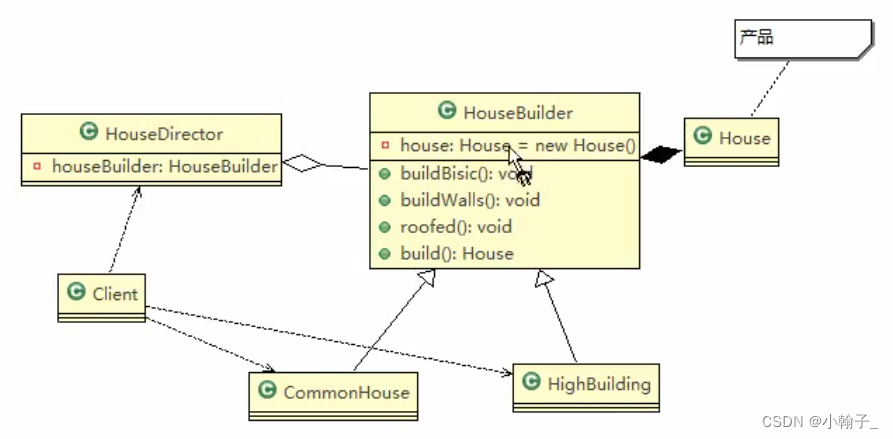
Java设计模式 04-建造者模式
建造者模式 一、 盖房项目需求 1)需要建房子:这一过程为打桩、砌墙、封顶 2)房子有各种各样的,比如普通房,高楼,别墅,各种房子的过程虽然一样,但是要求不要相同的. 3)请编写程序,完成需求. …...

安语未公告于2023年3月20日发布
因一些特殊原因,凡事都是有开始,高潮和结束三大过程,做出以下决定: 所有对 安语未文章 为之热爱、鞭策、奉献,和支持过的开发者: 注:所有资源以及资料都会正常下载和查看 如需联系࿱…...

进销存是什么?如何选择进销存系统?
什么是进销存?进销存软件概念起源于上世纪80年代,由于电算化的普及,计算机管理的推广,不少企业对于仓库货品的进货,存货,出货管理,有了强烈的需求,进销存软件的发展从此开始。 进入…...

基于BP神经网络的图像跟踪,基于BP神经网络的细胞追踪识别
目录 摘要 BP神经网络的原理 BP神经网络的定义 BP神经网络的基本结构 BP神经网络的神经元 BP神经网络激活函数及公式 基于BP神经网络的细胞识别追踪 matab编程代码 效果 结果分析 展望 摘要 智能驾驶,智能出行是现代社会发展的趋势之一,其中,客量预测对智能出行至关重要,…...
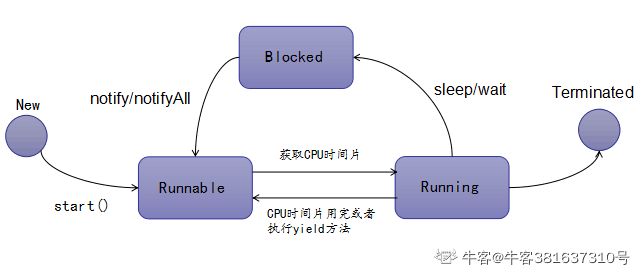
Java面试总结篇
引用介绍 1.线程安全不安全的概念 线程安全: 指多个线程在执行同一段代码的时候采用加锁机制,使每次的执行结果和单线程执行的结果都是一样的,不存在执行程序时出现意外结果。 线程不安全: 是指不提供加锁机制保护,有可能出现多个线程先后更改数据造成所得到的数据是脏…...
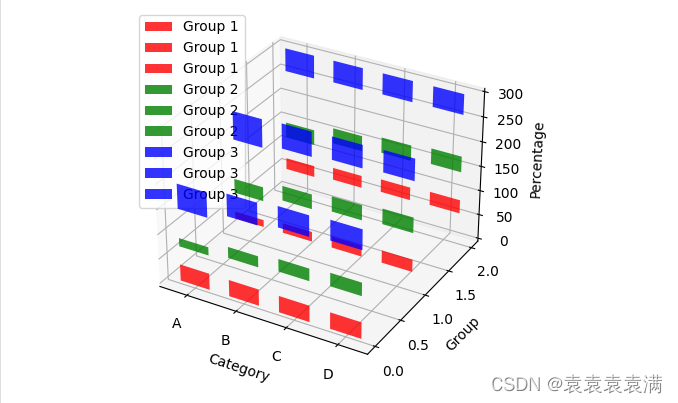
100天精通Python(可视化篇)——第80天:matplotlib绘制不同种类炫酷柱状图代码实战(簇状、堆积、横向、百分比、3D柱状图)
文章目录0. 专栏导读1. 普通柱状图2. 簇状柱形图3. 堆积柱形图4. 横向柱状图5. 横向双向柱状图6. 百分比堆积柱形图7. 3D柱形图8. 3D堆积柱形图9. 3D百分比堆积柱形图0. 专栏导读 🏆🏆作者介绍:Python领域优质创作者、CSDN/华为云/阿里云/掘金…...

【Java】UDP网络编程
文章目录前言DatagramSocketDatagramPacket注意事项与区别代码演示前言 UDP(user datagram protocol)的中文叫用户数据报协议,属于传输层。 UDP是面向非连接的协议,它不与对方建立连接,而是直接把我要发的数据报发给对…...
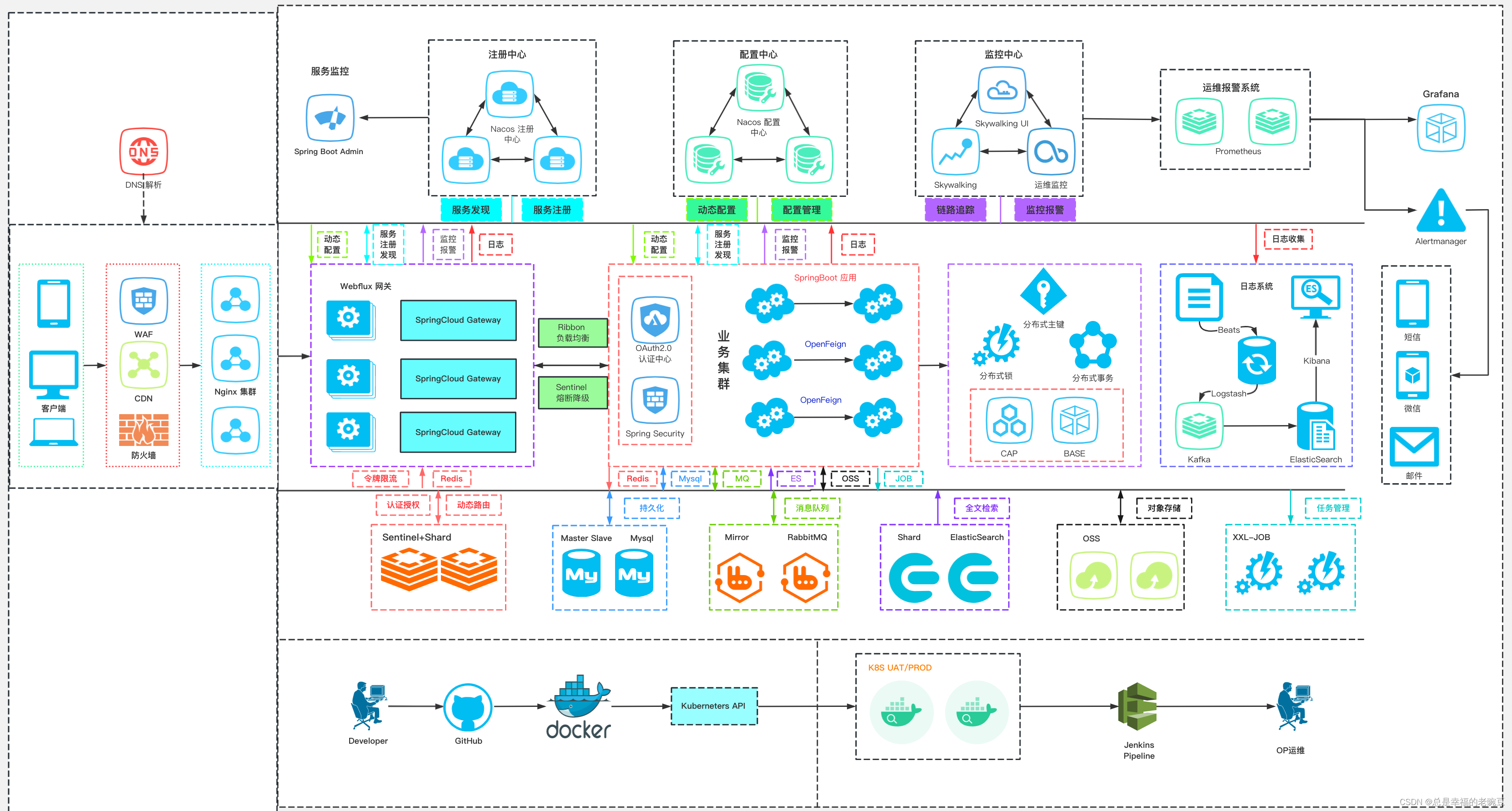
Springboot源代码总结
前言 编写微服务,巩固知识 文章目录 前言springboot原理springboot启动流程SpringBoot自动配置底层源码解析自动配置到底配了什么?自动配置类条件注解Starter机制@ConditionalOnMissingBeanSpringBoot启动过程源码解析构造SpringApplication对象SpringBoot完整的配置优先级s…...
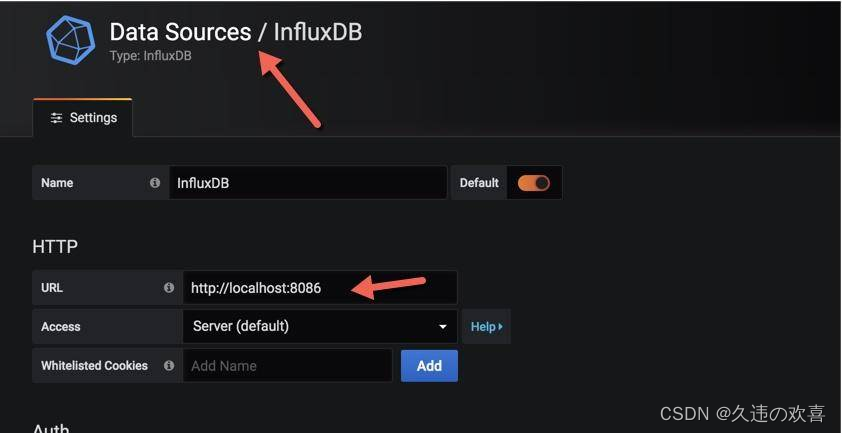
JVM监控搭建
文章目录JVM监控搭建整体架构JolokiaTelegrafInfluxdbGrafanaJVM监控搭建 整体架构 JVM 的各种内存信息,会通过 JMX 接口进行暴露。 Jolokia 组件负责把 JMX 信息翻译成容易读取的 HTTP 请求。Telegraf 组件作为一个通用的监控 agent,和 JVM 进程部署在…...

java中如何优化大量的if...else...
目录 策略模式(Strategy Pattern) 工厂模式(Factory Pattern) 映射表(Map) 数据驱动设计(Data-Driven Design) 策略模式(Strategy Pattern) 将每个条件分…...
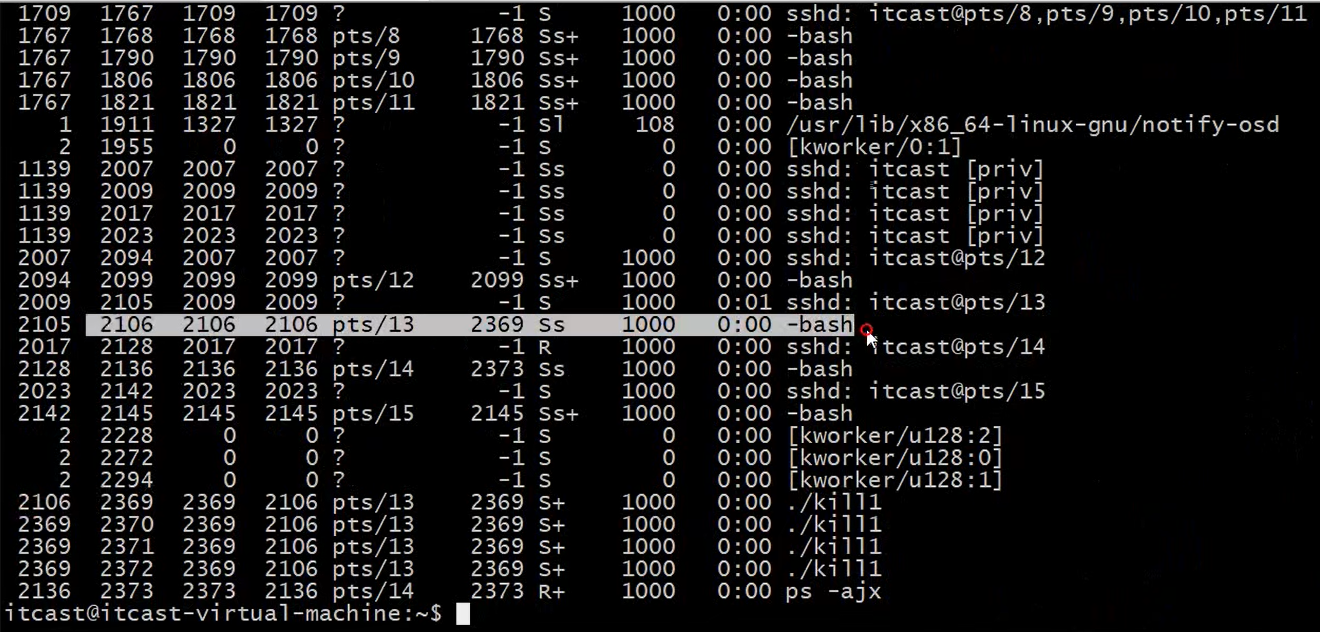
24. linux系统基础
两个进程间想通讯,必须要通过内核,今天讲的信号其实本质也是讲进程间通讯的意思,那么你为什么可以在shell环境下,可以和一个进程发kill-9啊? shell是不是相当于一个进程?你自己运行的那个进程是不是也相当于…...

【C++】面试101,二叉搜索树的最近公共祖先,在二叉树中找到两个节点的最近公共祖先,序列化二叉树,重建二叉树,输出二叉树的右视图,组队竞赛,删除公共字符
目录 1.二叉搜索树的最近公共祖先 2.在二叉树中找到两个节点的最近公共祖先 3.序列化二叉树 4.重建二叉树 5.输出二叉树的右视图 6.组队竞赛 7.删除公共字符 1.二叉搜索树的最近公共祖先 这是一个简单的问题,因为是二叉搜索树(有序)&am…...

Java常见面试题及解答
Java常见面试题及解答1 面向对象的三个特征2 this,super关键字3 基础数据类型4 public、protected、default、private5 接口6 抽象类6.1 抽象类和接口的区别7 重载(overload)、重写(override)8 final、finalize、final…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
