【C++】面试101,用两个栈实现队列,包含min函数的栈,有效括号序列,滑动窗口的最大值,最小的K个数,倒置字符串,排序子序列,跳跃,数字三角形,蓝肽子序列
目录
1. 用两个栈实现队列
2.包含min函数的栈
3.有效括号序列
4.滑动窗口的最大值
5.最小的K个数
6.倒置字符串
7.排序子序列
8.数字三角形(蓝桥杯,学习一个大佬的博客....)
9.跳跃(蓝桥杯)
10.蓝肽子序列
1. 用两个栈实现队列
之前我们C实现过一次
但是当时手搓的栈和队列....
现在我们开始C++实现一把
一个栈可以实现队列的push,但是由于两种数据结构的性质,一个栈不能满足先进先出
加入辅助栈
把队列栈的数据导入辅助栈,这时候栈顶pop就可以成功删除
例如:队列栈push: 1 2 3
正确pop:1 2 3
现在辅助栈是空,把队列栈数据导入:3 2 1
删除辅助栈栈顶:1 2 3
只要辅助栈为空,就一次性导入所有队列栈元素
辅助栈不为空,优先pop辅助栈数据,因为这可能是上一个残留元素,顺序不能乱

class Solution
{
public:void push(int node) {stack1.push(node); //随便选一个栈作为构建队列的栈(队列栈),这里选stack2也可以,但是下面所有都要换}int pop() {if (stack2.empty()) //如果辅助栈是空 {while (!stack1.empty()) //当队列栈不是空{stack2.push(stack1.top()); //把队列栈导入辅助栈stack1.pop();}}int ans = stack2.top();//辅助栈pop顺序是要删除的顺序stack2.pop();return ans;}private:stack<int> stack1;stack<int> stack2;
};2.包含min函数的栈
现在还记得C写的阴影
用C++实现一下
真的很简单啊,push函数,只要min栈为空或者现在要入的值<=min栈栈顶元素,那么入栈
class Solution {
public:void push(int value) {s.push(value);if(_min.empty()||value<=_min.top())_min.push(value);}void pop() {int top=s.top(); s.pop();if(top==_min.top())_min.pop();}int top() {return s.top();}int min() {return _min.top();}stack <int> s;stack<int> _min;
};3.有效括号序列
首先碰到左括号入栈,如果遇到右括号,栈为空或者栈顶不是和他匹配的左括号,那么直接false
遍历字符串结束之后,如果栈是不是空,证明左括号没有匹配完全,那么false
bool isValid(string s) {// write code herestack<char> st;for(int i=0;i<s.size();i++){if(s[i]=='{' || s[i]=='[' || s[i]=='(')st.push(s[i]);if(s[i]==']'){if(st.empty()||st.top()!='[')return false;st.pop();}else if(s[i]=='}'){if(st.empty()||st.top()!='{')return false;st.pop();}if(s[i]==')'){if(st.empty()||st.top()!='(')return false;st.pop();}}if(st.empty()) return true;return false;}4.滑动窗口的最大值
这个题我是暴力写的,直接挨个遍历每个窗口,找里面的最大
vector<int> maxInWindows(const vector<int>& num, unsigned int size) {vector<int > v;if(size==0 || size>num.size()) return v;for(int i=0;i<num.size()-size+1;i++){int max=num[i];for(int j=i;j<size+i;j++)if(num[j]>max) max=num[j];v.push_back(max);}return v;}学习一下大佬们的代码
其实就是把我们的思路写在队列...
vector<int> maxInWindows(const vector<int>& num, unsigned int size) {// vector<int > v;// if(size==0 || size>num.size()) return v;// for(int i=0;i<num.size()-size+1;i++)// {// int max=num[i];// for(int j=i;j<size+i;j++)// if(num[j]>max) max=num[j];// v.push_back(max);// }// return v;vector<int> ans;queue<int> q;if(size==0 || size>num.size()) return ans;for(int i=0;i<num.size()&&i+size<=num.size();i++){q.push(num[i]);for(int j=i;j<i+size;j++){if(num[j]>q.front()){q.pop();q.push(num[j]);}}ans.push_back(q.front());while(!q.empty())q.pop();}return ans;}5.最小的K个数
其实就是建大堆,把最小的前k入到优先级队列(默认大堆)
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {vector<int > ans;if(!k) return ans;priority_queue<int> pq;for(int i=0;i<k;i++){pq.push(input[i]);}for(int j=k;j<input.size();j++){if(input[j]<pq.top()){pq.pop();pq.push(input[j]);}}while(!pq.empty()){ans.push_back(pq.top());pq.pop();}return ans;}6.倒置字符串
之前用C实现过,真的不好理解,很绕
但是这次用C++
oj最好不要cin>>s,其中s是一个字符串,用getline函数

#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
using namespace std;int main1()
{string s1;while (getline(cin, s1)){reverse(s1.begin(), s1.end());//将整个句子逆置auto start = s1.begin();for (int i = 0;s1.begin()+i!=s.end()+1; i++)//可能不会直接到end(){if (s1[i] == ' '){auto end = s1.begin() + i;reverse(start, end);//将每个单词逆置回来,逆置空格前的字符串start = end + 1;//跳过空格进入下一个单词}if(s1.begin() + i == s1.end())//最后一个单词找没有空格,所以找到s1.end()进行逆置{reverse(start, s1.end());}}cout << s1 << endl;}return 0;
}
7.排序子序列
一定要注意,在一个非递增/非递减的区间里,是可以有重复的元素,但是在遍历整个数组的时候,遇到重复元素直接跳过!因为你放哪个区间都不合适,还会影响子序列的判断
#include<iostream>
#include<vector>using namespace std;int main(){int n;cin >> n;vector<int> a;a.resize(n + 1);a[n] = 0;int i = 0;for (i = 0; i < n; ++i){cin >> a[i];}i = 0;int count = 0;while (i < n){// 非递减子序列if (a[i] < a[i + 1]){while (i < n && a[i] <= a[i + 1]){i++;}count++;i++;}else if (a[i] == a[i + 1]){i++;}else // 非递增子序列{while (i < n && a[i] >= a[i + 1]){i++;}count++;i++;}}cout << count << endl;return 0;}8.数字三角形(蓝桥杯,学习一个大佬的博客....)
首先观察到这个题目要求

所以写一个dfs的代码,看一下最后的结果应该是什么样的
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int n;
vector< vector<bool> >flag(101);void dfs(int i, int j, int time)//向左,time-1;向右,time+1
{if (flag[i][j])//若当前点已递归过,则直接返回(降低时间复杂度)return;flag[i][j] = true;//当前点满足if (time == -1 && i + 1 < n)//必须向右dfs(i + 1, j + 1, 0);//向右下方点递归else if (time == 1 && i + 1 < n)//必须向左dfs(i + 1, j, 0);//向左下方点递归else if (!time && i + 1 < n)//可向左也可向右{dfs(i + 1, j + 1, 1);dfs(i + 1, j, -1);}else//其他情况则返回return;
}int main()
{cin >> n;for (int i = 0; i < n; i++)for (int j = 0; j < i + 1; j++)flag[i].push_back(false);//初始化为falsedfs(0, 0, 0);//从第一个点往下递归//输出结果for (int i = 0; i < n; i++){for (int j = 0; j < i + 1; j++)if (flag[i][j])cout << "1 ";elsecout << "0 ";cout << endl;}cout << endl << endl;return 0;
}
这个是n=11的代码![]()

n=10![]()
发下规律,然后从倒数第二行往上动态规划
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int n, tmp;
vector< vector<int> >num(101);
vector< vector<bool> >flag(101);int main()
{// 请在此输入您的代码cin >> n;for (int i = 0; i < n; i++)for (int j = 0; j < i + 1; j++){cin >> tmp;num[i].push_back(tmp);flag[i].push_back(false);}if (n % 2) //n为奇数,则最后一行有奇数个数,最中间的数可作为终点flag[n - 1][(n - 1) / 2] = true;else //i为偶数,则最后一行有偶数个数,最中间两个数可作为终点{flag[n - 1][n / 2] = true;flag[n - 1][n / 2 - 1] = true;}for (int j = 0; j < n; j++)//最后一行其余的数设为0if (!flag[n - 1][j])num[n - 1][j] = 0;for (int i = n - 2; i >= 0; i--)//从倒数第二行往上遍历{for (int j = 0; j <= i; j++)//从左往右遍历{if (!flag[i + 1][j] && !flag[i + 1][j + 1])//该点不能到达num[i][j] = 0;//设为0,方便计算else //该点能到达{num[i][j] += max(num[i + 1][j], num[i + 1][j + 1]);//取两者最大即可flag[i][j] = true;//标记该点能到达}}}cout << num[0][0] << endl;//输出结果return 0;
}
9.跳跃(蓝桥杯)
#include <iostream>
#include <algorithm>
#include "string.h"
#include <climits>
#include <vector>
using namespace std;int n, m;
vector< vector<int> >weight(101);//每个点的权值
vector< vector<long long> >totoal_weight(101);//存储走到每个点的最大权值和long long find_max(int x, int y)//找到走到该点的所需的最大权值和(不包括该点的权值)
{long long max = LLONG_MIN;for (int i = x; i >= 1; i--)//从该点往上{for (int j = y; j >= 1; j--)//从该点往左{//1.不能原地踏步,所以不能与该点坐标一样//2.步数要小于等于3//3.要比当前的max大才更新maxif (!(x == i && y == j) && (x - i + y - j) <= 3 && max < totoal_weight[i][j])max = totoal_weight[i][j];}}if (max == LLONG_MIN)//说明是起点,返回0即可return 0;else //返回走到该点所需的最大权值和(不包括该点的权值)return max;
}int main()
{cin >> n >> m;int w;//临时变量,某点的权值for (int i = 1; i <= n; i++) //行输入{weight[i].push_back(0); //占位,因为j要从1开始,而数组下标从0开始totoal_weight[i].push_back(0); //占位for (int j = 1; j <= m; j++) //列输入{cin >> w;weight[i].push_back(w); totoal_weight[i].push_back(w);}}for (int i = 1; i <= n; i++) //从上往下{ for (int j = 1; j <= m; j++) //从左往右{totoal_weight[i][j] += find_max(i, j);//得到每个点的最大权值和}}cout << totoal_weight[n][m] << endl; //输出最后一个点的最大权值和return 0;
}10.蓝肽子序列
#include <iostream>
#include <algorithm>
using namespace std;
int dp[1005][1005];
string s1, s2;
string str1[1005], str2[1005];
int cnt1, cnt2;
int main()
{cin >> s1 >> s2;int d1 = s1.length(), d2 = s2.length();for (int i = 0; i < d1;){cnt1++;if (s1[i] >= 'A' && s1[i] <= 'Z'){str1[cnt1] += s1[i++];while (s1[i] >= 'a' && s1[i] <= 'z'){str1[cnt1] += s1[i++];}}}for (int i = 0; i < d2;){cnt2++;if (s2[i] >= 'A' && s2[i] <= 'Z'){str2[cnt2] += s2[i++];while (s2[i] >= 'a' && s2[i] <= 'z'){str2[cnt2] += s2[i++];}}}for (int i = 1; i <= cnt1; i++)for (int j = 1; j <= cnt2; j++){if (str1[i] == str2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);}cout << dp[cnt1 ][cnt2 ] << endl;return 0;
}
相关文章:

【C++】面试101,用两个栈实现队列,包含min函数的栈,有效括号序列,滑动窗口的最大值,最小的K个数,倒置字符串,排序子序列,跳跃,数字三角形,蓝肽子序列
目录 1. 用两个栈实现队列 2.包含min函数的栈 3.有效括号序列 4.滑动窗口的最大值 5.最小的K个数 6.倒置字符串 7.排序子序列 8.数字三角形(蓝桥杯,学习一个大佬的博客....) 9.跳跃(蓝桥杯) 10.蓝肽子序列 1. 用…...

WPF 认识WPF
什么是WPF?WPF是Windows Presentation Foundation(Windows展示基础)简称,顾名思义是专门编写表示层的技术。WPF绚丽界面如下:GUI发展及WPF历史?Windows系统平台上从事图形用户界面GUI(Graphic User Interface)已经经历了多次换代,…...

【建议收藏】PHP单例模式详解以及实际运用
PHP单例模式详解以及实际运用 什么是单例模式? 首先我们百度百科他怎么说? 单例模式,属于创建类型的一种常用的软件设计模式。通过单例模式的方法创建的类在当前进程中只有一个实例(根据需要,也有可能一个线程中属于单例,如&a…...

【十二天学java】day04-流程控制语句
第一章 流程控制语句 在一个程序执行的过程中,各条语句的执行顺序对程序的结果是有直接影响的。所以,我们必须清楚每条语句的执行流程。而且,很多时候要通过控制语句的执行顺序来实现我们想要的功能。 1.1 流程控制语句分类 顺序结构 判断…...
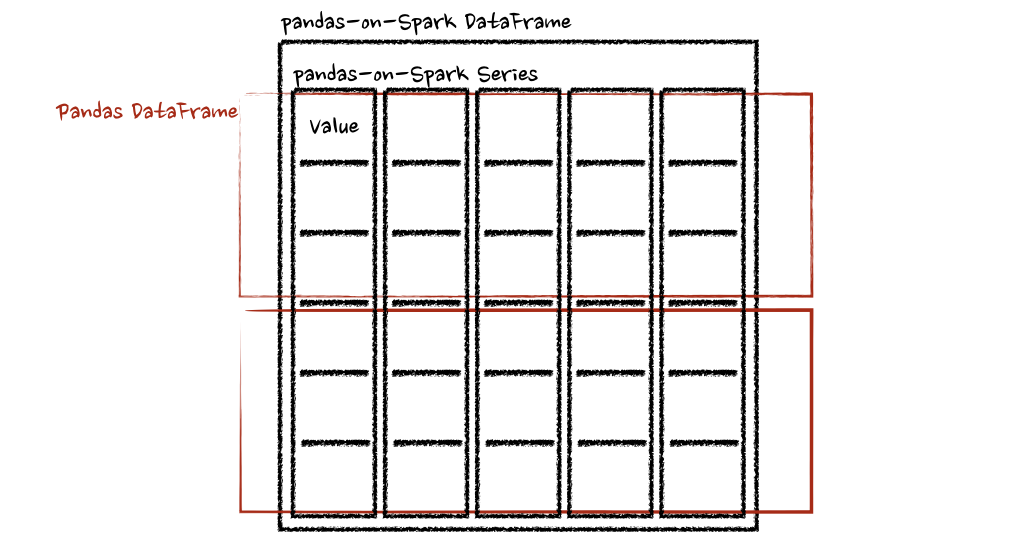
Pandas 与 PySpark 强强联手,功能与速度齐飞
Pandas做数据处理可以说是yyds!而它的缺点也是非常明显,Pandas 只能单机处理,它不能随数据量线性伸缩。例如,如果 pandas 试图读取的数据集大于一台机器的可用内存,则会因内存不足而失败。 另外 pandas 在处理大型数据…...

【Zabbix实战之部署篇】docker部署Zabbix+grafana监控平台
【Zabbix实战之部署篇】docker部署Zabbix+grafana监控平台 一、Zabbix介绍1.Zabbix简介2.Zabbix的优点3.Zabbix各组件介绍4.Zabbix架构图二、grafana介绍1.grafana简介2.grafana特点三、实践环境规划四、检查本地docker环境1.检查操作系统版本2.检查docker版本3.检查docker服务…...
acm省赛:高桥和低桥(三种做法:区间计数、树状数组、线段树)
题目描述 有个脑筋急转弯是这样的:有距离很近的一高一低两座桥,两次洪水之后高桥被淹了两次,低桥却只被淹了一次,为什么?答案是:因为低桥太低了,第一次洪水退去之后水位依然在低桥之上ÿ…...

stm32-定时器详解
0. 概述 本文针对STM32F1系列,主要讲解了其中的8个定时器的原理和功能 1. 定时器分类 STM32F1 系列中,除了互联型的产品,共有 8 个定时器,分为基本定时器,通用定时器和高级定时器基本定时器 TIM6 和 TIM7 是一个 16 位…...
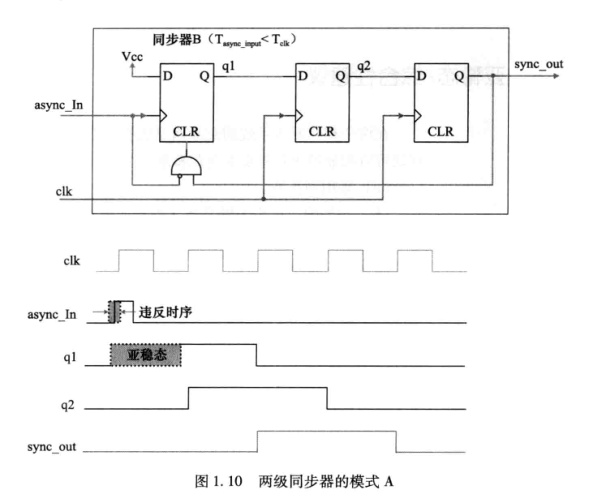
《硬件架构的艺术》读书笔记:Chapter 1 亚稳态的世界
Chapter 1 亚稳态的世界 一、简介 同步系统中,数据和时钟有固定的因果关系(在同一时钟域(Clock Domains))中,只要数据和时钟满足建立时间和保持时间的要求,不会产生亚稳态(meastable) 静态时序分析(STA) 就是基于同步电路设计模型而出现的&am…...
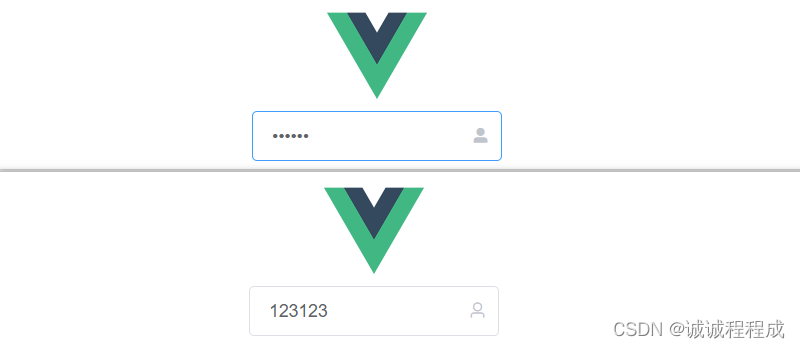
开箱即用的密码框组件
写了一个小玩具,分享一下 - 组件功能: 初次进入页面时,密码隐藏显示,且无法查看真实密码 当修改密码时,触发键盘,输入框则会直接清空 此时输入密码,可以设置密码的隐藏或显示: …...

ChatGPT能否取代程序员?
目录ChatGPT能否取代程序员?ChatGPT和程序员的工作内容和工作方式ChatGPT和程序员的共同点程序员的优势程序员的实力ChatGPT和程序员的关系结论惊喜ChatGPT能否取代程序员? ChatGPT是一种非常普遍的人工智能(AI)系统,…...

案例分享 | 金融微服务场景下如何提升运维可观测性
云原生环境下金融业务的微服务化改造以及分布式架构的部署,使得业务与开发部门的关联更为紧密,传统运维监控已满足不了业务运营需求,亟需建设具备可观测性的运维体系。所以这次我们以某金融客户的实践案例为例,跟大家说一说在金…...
)
CentOS8提高篇3:Centos8安装播放器(mplayer vlc)
1. 准备工作(需要配置epel, rpmfusion源); 配置epel源 下载epel dnf install epel-release 配置rpmfusion源 下载rpmforge dnf install rpmfusion-free-release-8.noarch.rpm 2. 安装mplayer和vlc 直接dnf安装 # dnf install mplayer # dnf install v…...

MySQL-存储过程
什么是存储过程我们前面所学习的MySQL语句都是针对一个表或几个表的单条 SQL 语句,但是在数据库的实际操作中,并非所有操作都那么简单,经常会有一个完整的操作需要多条SQL语句处理多个表才能完成。例如,为了确认学生能否毕业&…...
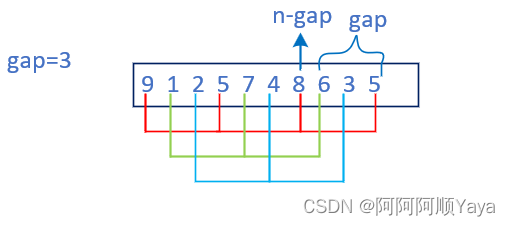
经典七大比较排序算法 · 下 + 附计数和基数排序
经典七大比较排序算法 下 附计数和基数排序1 插入排序1.1 算法思想1.2 代码实现1.3 插入排序特性2 希尔排序2.1 算法思想2.2 代码实现2.3 希尔排序特性3 七大比较排序特性总结4 计数排序4.1 算法思想4.2 代码实现4.3 计数排序特性5 基数排序5.1 算法思想5.2 代码实现1 插入排…...
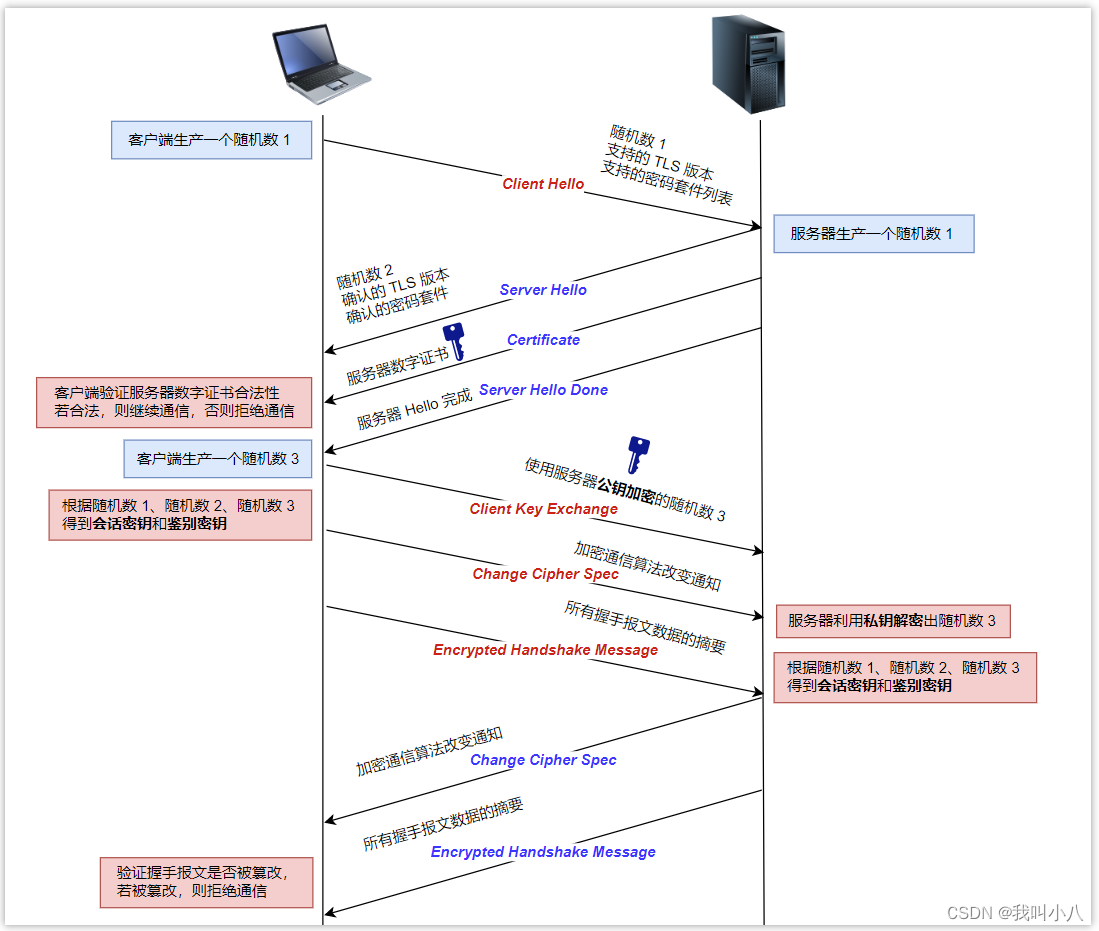
HTTPS协议,看这篇就够了
不安全的HTTP 近些年来,越来越多的网站使用 HTTPS 协议进行数据传输,原因在于 HTTPS 相较于 HTTP 能够提供更加安全的服务。 很多浏览器对于使用 HTTP 协议的网站会加上『警告』的标志表示数据传输不安全,而对于使用 HTTPS 协议的网站会加上…...

C语言学习之路--结构体篇
目录一、前言二、结构体的声明1、结构的基础知识2、结构的声明3、结构体成员的类型4、结构体变量的定义和初始化三、结构体成员的访问四、结构体传参一、前言 本人是一名小白,这一篇是记录我C语言学习中的结构体的所学所得,仅为简单的认识下C语言中的各…...
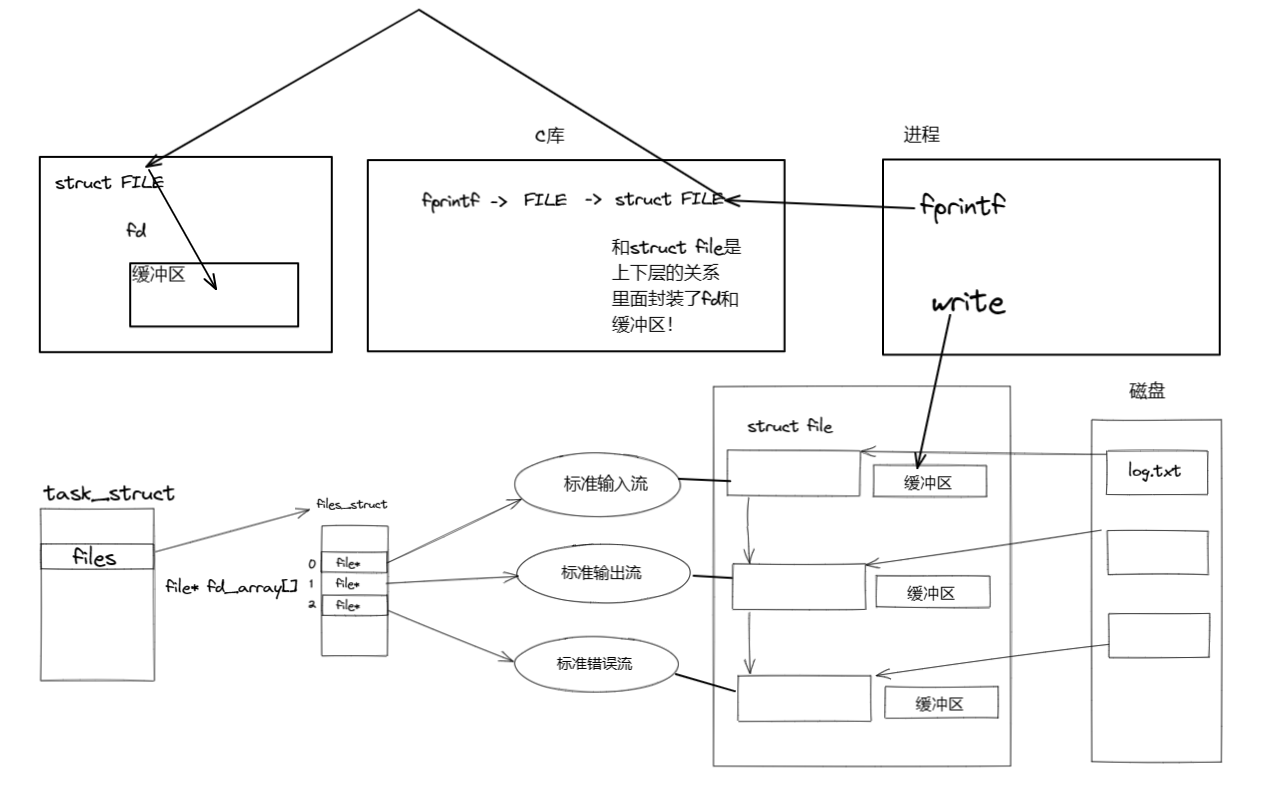
【LINUX】初识文件系统
文章目录一、前言二、回顾C语言文件操作三、初识系统调用openreadwriteclose四、文件系统初识五、结语一、前言 二、回顾C语言文件操作 int main() {FILE* fp fopen("log.txt", "w");if (fp NULL){perror("fopen");}int cnt 0;fputs("…...

金三银四Java面试题及答案整理(2023最新版) 持续更新
作为一名优秀的程序员,技术面试是不可避免的一个环节,一般技术面试官都会通过自己的方式去考察程序员的技术功底与基础理论知识。 如果你参加过一些大厂面试,肯定会遇到一些这样的问题: 1、看你项目都用的框架,熟悉 …...

7个角度,用 ChatGPT 玩转机器学习
大家好,我是机器学习科普创作者章北海mlpy,探索更高效的学习方法是我一直等追求。现在的初学者太幸福了,可以利用ChatGPT来帮助你学习机器学习的各个方面。 比如【个人首测】百度文心一言 VS GPT-4这篇文章中,我就用文心一言、GP…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
