当前位置： 首页 > news >正文

书生大模型学习笔记2 - Python

news 2026/2/9 12:14:20

Python实现wordcount

请实现一个wordcount函数，统计英文字符串中每个单词出现的次数。返回一个字典，key为单词，value为对应单词出现的次数。
解题思路：首先把字母转小写>然后把单词取出来去除标点>循环单词列表>key已存在则value+1否则添加key
在这里插入图片描述

VScode连接InternStudio debug笔记

  1. VScode连接到开发机（具体方法见上一篇文章）

  2. 安装图中两个python插件
    在这里插入图片描述

  3. 创建debug配置文件
    在这里插入图片描述在这里插入图片描述

  4. pip安装debugpy

    pip install debugpy

  5. 命令行启动debug server

    python -m debugpy --listen 5678 --wait-for-client ./learning/wordcount.py

  6. 开始debug
    在这里插入图片描述
    在这里插入图片描述

    debug面板各按钮功能介绍：

    1: continue: 继续运行到下一个断点
    2: step over：跳过，可以理解为运行当前行代码，不进入具体的函数或者方法。
    3: step into: 进入函数或者方法。如果当行代码存在函数或者方法时，进入代码该函数或者方法。如果当行代码没有函数或者方法，则等价于step over。
    4: step out：退出函数或者方法, 返回上一层。
    5: restart：重新启动debug

相关文章：

书生大模型学习笔记2 - Python

Python实现wordcount 请实现一个wordcount函数，统计英文字符串中每个单词出现的次数。返回一个字典，key为单词，value为对应单词出现的次数。 解题思路：首先把字母转小写>然后把单词取出来去除标点>循环单词列表>key已存…...

编程日记 2024/8/6 21:06:31

JavaScript三级联动jQuery写法

HTML结构 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>三级联动</title><!-- <style…...

编程日记 2024/8/6 21:03:28

无人机挂载抓捕网

一、技术原理与机制 无人机挂载抓捕网装置的技术原理是通过无人机平台的飞行能力和灵活性&#xff0c;结合特制的抓捕网装置&#xff0c;实现对目标的快速、准确抓捕。抓捕网装置在接收到指令后&#xff0c;通过特定机制快速展开并包围目标&#xff0c;从而实现抓捕任务。 二…...

编程日记 2024/8/6 21:02:27

174.地下城游戏——LeetCode

题目 恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里&#xff0c;他必须穿过地下城并通过对抗恶魔来拯救公主。 骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻…...

编程日记 2024/8/6 21:01:26

登录相关功能的优化【JWT令牌+拦截器+跨域】

登录相关功能的优化 登录后显示当前登录用户el-dropdown: Element - The worlds most popular Vue UI framework <el-dropdown style"float: right; height: 60px; line-height: 60px"><span class"el-dropdown-link" style"color: white;…...

编程日记 2024/8/6 21:00:25

向日葵没有显示器会卡住

前言 有一台机器【ubuntu20】&#xff0c;用于远程开发&#xff0c;使用向日葵时候&#xff0c;如果不接显示器是会卡住的。。。 显示屏是有限的&#xff0c;所以现在解决一下这个问题。 卡在登录界面 双击启动 由于Ubuntu默认显示管理器是gdm&#xff0c;而向日葵使用的是l…...

编程日记 2024/8/6 20:57:22

【机器学习西瓜书学习笔记——聚类】

机器学习西瓜书学习笔记【第九章】 第九章 聚类9.1 聚类任务9.2 性能度量两类指标 9.3距离计算基本性质属性有序属性无序属性 混合距离加权距离 9.4 原型聚类K-MEANS聚类算法步骤优势劣势 学习向量量化高斯混合聚类步骤难点例子EM思想的体现小结 9.5 密度聚类9.6 层次聚类 第九…...

编程日记 2024/8/6 20:55:20

MATLAB（8）深度变化模型

一、前言 在MATLAB中模拟深度变化模型通常依赖于具体的应用场景&#xff0c;比如海洋深度、地下水深度、地形高度变化等。由于“深度变化”可以涉及多种物理过程和数学模型&#xff0c;我将提供一个简化的示例&#xff0c;该示例模拟了一个基于时间变化的深度变化模型&#xff…...

编程日记 2024/8/6 20:53:18

mp3格式转换器哪个好用？汇总七款音频格式转换方法（无损转换）

音乐已经成为我们生活中不可或缺的一部分。但是在播放的时候&#xff0c;可能会遇到音频格式不兼容的情况。特别是在一些下载站或音乐平台获取的音频&#xff0c;有些特殊格式在播放器上无法正常播放&#xff0c;一般这种情况我们需要借助mp3转换器解决。 mp3是一种常见的数字音…...

编程日记 2024/8/6 20:52:17

移行前的复盘：CodeCommit 的重要地位分析

前言 截至7月28日&#xff0c;关于AWS CodeCommit的现状如下&#xff1a; 现有账号的现有存储库可以继续使用CodeCommit&#xff0c;不受限制。之前未使用过CodeCommit的账号&#xff08;或没有现有存储库的账号&#xff09;无法创建新的存储库。 这并不意味着CodeCommit的服…...

编程日记 2024/8/6 20:51:16

Java中等题-括号生成（力扣）

数字 n 代表生成括号的对数&#xff0c;请你设计一个函数&#xff0c;用于能够生成所有可能的并且 有效的 括号组合。 示例 1&#xff1a; 输入&#xff1a;n 3 输出&#xff1a;["((()))","(()())","(())()","()(())","()()(…...

编程日记 2024/8/6 20:50:15

Flink 实时数仓（八）【DWS 层搭建（二）流量域、用户域、交易域搭建】

前言 今天的任务是完成流量域最后一个需求、用户域的两个需求以及交易域的部分需求&#xff1b; 1、流量域页面浏览各窗口汇总表 任务&#xff1a;从 Kafka 页面日志主题读取数据&#xff0c;统计当日的首页和商品详情页独立访客数。 注意&#xff1a;一般我们谈到访客&…...

编程日记 2024/8/6 20:48:13

gitlab-runner /var/run/docker.sock connect permission denied

usermod -aG docker gitlab-runner sudo service docker restart参考&#xff1a;https://gitlab.com/gitlab-org/gitlab-runner/-/issues/3492...

编程日记 2024/8/6 20:46:11

网络安全 - 应急响应检查表

前言 本项目旨在为应急响应提供全方位辅助&#xff0c;以便快速解决问题。结合自身经验和网络资料&#xff0c;形成检查清单&#xff0c;期待大家提供更多技巧&#xff0c;共同完善本项目。愿大家在应急之路一帆风顺。 图片皆来源于网络&#xff0c;如有侵权请联系删除。 一…...

编程日记 2024/8/6 20:45:10

AD常用PCB设计规则介绍 （详细版）

AD09常用PCB设计规则介绍 电气设计规则用来设置在电路板布线过程中所遵循的电气方面的规则&#xff0c;包括安全间距、短路、未布线网络和未连接引脚这四个方面的规则&#xff1a; &#xff08;1&#xff09;、安全间距规则(clearance) 该规则用于设定在PCB设计中&#xff0…...

编程日记 2024/8/6 20:42:05

mysql主从服务配置

主从MySQL服务器 [rootlocalhost ~]# yum -y install ntpdate [rootlocalhost ~]# ntpdate cn.ntp.org.cn [rootlocalhost ~]# yum -y install rsync [rootlocalhost ~]# vim mysql.sh #!/bin/bash yum list installed |grep libaio if [ $? ne 0 ]; then yum -y install…...

编程日记 2024/8/6 20:41:03

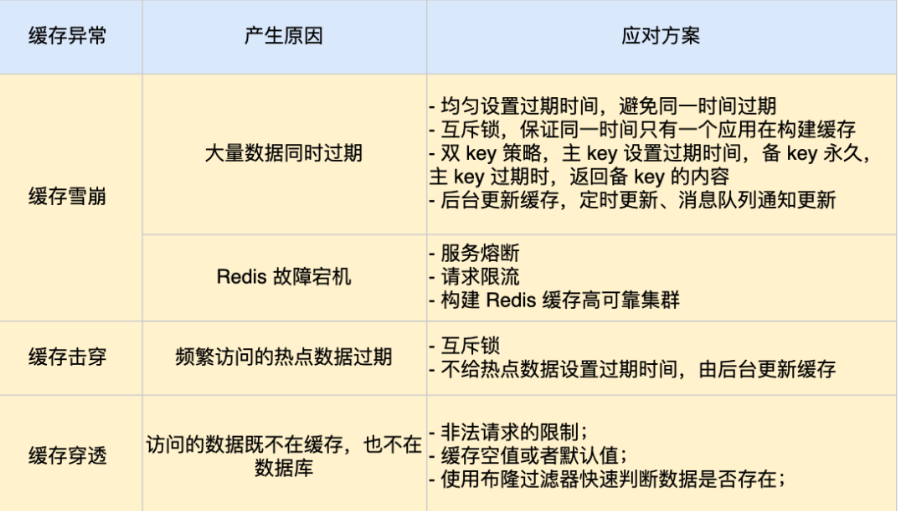
Redis基础总结、持久化、主从复制、哨兵模式、内存淘汰策略、缓存

文章目录 Redis 基础Redis 是什么&#xff0c;有哪些特点为什么要使用 Redis 而不仅仅依赖 MySQLRedis 是单线程吗Redis 单线程为什么还这么快 Redis 数据类型和数据结构五种基本数据结构及应用场景其他数据类型Redis 底层数据结构 Redis 持久化数据不丢失的实现AOF 日志RDB 快…...

编程日记 2024/8/6 20:40:02

Java与Python优劣势对比：具体例子与深入分析

在软件开发的世界里&#xff0c;Java和Python是两座不可忽视的高峰。它们各自拥有独特的优势和应用场景&#xff0c;为开发者提供了多样化的选择。本文将通过具体例子&#xff0c;深入分析Java和Python在不同方面的表现&#xff0c;以期为读者提供更为详尽的参考。 1. 语法简洁…...

编程日记 2024/8/6 20:38:01

C++内存泄漏介绍

C内存泄漏&#xff08;Memory Leak&#xff09;是指程序在运行过程中&#xff0c;动态分配的内存没有被适当地释放或回收&#xff0c;导致这部分内存始终被占用&#xff0c;无法再被程序或其他程序使用。这种情况通常发生在使用了new或malloc等函数动态分配内存后&#xff0c;忘…...

编程日记 2024/8/6 20:37:00

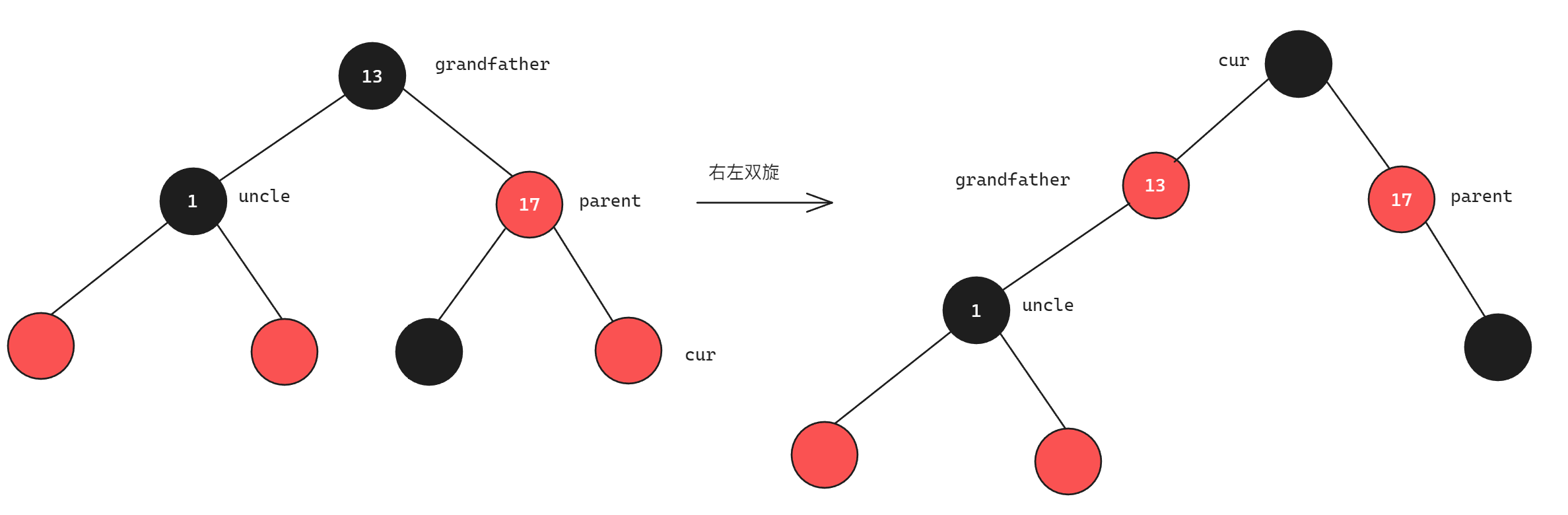
C++分析红黑树

目录 红黑树介绍 红黑树的性质与平衡控制关系 红黑树节点的插入 情况1&#xff1a;不需要调整 情况2&#xff1a;uncle节点为红色 情况3&#xff1a;uncle节点为黑色 总结与代码实现 红黑树的删除&#xff08;待实现&#xff09; 红黑树的效率 红黑树介绍 红黑树是第二种平衡二…...

编程日记 2024/8/6 20:34:58

挑战杯推荐项目

“人工智能”创意赛 - 智能艺术创作助手&#xff1a;借助大模型技术&#xff0c;开发能根据用户输入的主题、风格等要求&#xff0c;生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用&#xff0c;帮助艺术家和创意爱好者激发创意、提高创作效率。 ​ - 个性化梦境…...

编程新知 2025/11/6 5:46:16

内存分配函数malloc kmalloc vmalloc

内存分配函数malloc kmalloc vmalloc malloc实现步骤： 1）请求大小调整：首先，malloc 需要调整用户请求的大小，以适应内部数据结构（例如，可能需要存储额外的元数据）。通常，这包括对齐调整，确保分配的内存地址满足特定硬件要求（如对齐到8字节或16字节边界）。 2）空闲…...

编程新知 2025/11/1 5:21:39

安宝特方案丨XRSOP人员作业标准化管理平台：AR智慧点检验收套件

在选煤厂、化工厂、钢铁厂等过程生产型企业&#xff0c;其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进&#xff0c;需提前预防假检、错检、漏检&#xff0c;推动智慧生产运维系统数据的流动和现场赋能应用。同时&#xff0c;…...

编程新知 2026/2/5 17:57:20

MODBUS TCP转CANopen 技术赋能高效协同作业

在现代工业自动化领域&#xff0c;MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步&#xff0c;这两种通讯协议也正在被逐步融合&#xff0c;形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

编程新知 2026/2/6 9:48:02

是否存在路径（FIFOBB算法）

题目描述 一个具有 n 个顶点e条边的无向图&#xff0c;该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序&#xff0c;确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数&#xff0c;分别表示n 和 e 的值&#xff08;1…...

编程新知 2025/10/1 6:09:21

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57

【7色560页】职场可视化逻辑图高级数据分析PPT模版

7种色调职场工作汇报PPT&#xff0c;橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版&#xff1a;职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

编程新知 2026/1/23 12:22:14

MySQL 知识小结（一）

一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库&#xff0c;分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷&#xff0c;但是文件存放起来数据比较冗余&#xff0c;用二进制能够更好管理咱们M…...

编程新知 2026/1/26 13:29:47

纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join

纯 Java 项目&#xff08;非 SpringBoot&#xff09;集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

编程新知 2025/9/26 12:26:35

华为OD机考-机房布局

import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

编程新知 2026/1/31 6:01:08