关于float浮点值二进制存储和运算精度损失的话题
1.前言
浮点值的存储、运算都可能会带来精度损失,了解精度损失背后的机制原因方便我们更好的了解什么情况下会发生精度损失、什么情况下精度损失较大,以及思考怎么避免或减少精度损失。
2.知识点
(1)IEEE 754标准
EEE 754标准(电气和电子工程师协会,简称IEEE)是目前通用的浮点数表示规范,它为单精度(float)、双精度(double)和扩展精度(如long double)浮点数定义了一套标准化的二进制编码方案。
根据该标准,浮点数可以表示为:
如5.5=![]()
(2)二进制排列规则
IEEE754 单精度(32位)的二进制排列规则:符号位S(1位,0为正数,1为负数) + 阶码E(8位) + 尾数M(23位)。
IEEE754 双精度(64位)的二进制排列规则:符号位S(1位,0为正数,1为负数) + 阶码E(11位) + 尾数M(52位)。
(3)阶码偏置
为了将阶码转换为无符号整数,以简化硬件实现,同时避免阶码出现特殊值0和255,设计了阶码偏置的规则。
单精度的偏置常数为127(固定值),即阶码 = 127 + 阶(左移为正数,右移为负数)。
双精度的偏置常数为1023(固定值),即阶码 = 1023 + 阶(左移为正数,右移为负数)。
根据上述知识点,float值的二进度排列如下图所示:

3. 示例
为方便理解,我们以float值98.204590为例进行二进制存储的说明。
步骤①:将整数部分整除以2,取余数部分倒序排列
98 / 2 = 49 余 0
49 / 2 = 24 余 1
24 / 2 = 12 余 0
12 / 2 = 6 余 0
6 / 2 = 3 余 0
3 / 2 = 1 余 1
1 / 2 = 0 余 1
整数部分二进制为:1100010。
步骤②:将小数部分乘以2,取商的整数部分正序排列( 一直乘 2 ,遇到 1 退出;如果乘 2 之后的数字大于 1,则减去 1 )
根据上述排列可知,尾数可以取23位,但由于小数点前面的1.不用显式表示,这样可以取24位,由于上面整数部分占据了7位,这样小数部分取17位:00110100011000000。
这样98.204590表示为:1100010.00110100011000000。
0.204590 * 2 = 0.40918 商的整数部分0
0.40918 * 2 = 0.81836 商的整数部分0
0.81836 * 2 = 1.63672 商的整数部分1
0.63672 * 2 = 1.27344 商的整数部分1
0.27344 * 2 = 0.54688 商的整数部分0
0.54688 * 2 = 1.09376 商的整数部分1
0.09376 * 2 = 0.18752 商的整数部分0
0.18752 * 2 = 0.37504 商的整数部分0
0.37504 * 2 = 0.75008 商的整数部分0
0.75008 * 2 = 1.50016 商的整数部分1
0.50016 * 2 = 1.00032 商的整数部分1
0.00032 * 2 = 0.00064 商的整数部分0
0.00064 * 2 = 0.00128 商的整数部分0
0.00128 * 2 = 0.00256 商的整数部分0
0.00256 * 2 = 0.00512 商的整数部分0
0.00512 * 2 = 0.01024 商的整数部分0
0.01024 * 2 = 0.02048 商的整数部分0
0.02048 * 2 = 0.04096 商的整数部分0
0.04096 * 2 = 0.08192 商的整数部分0
步骤③:小数点向左移,直到整数部分为1
1100010.00110100011000000处理后为1.10001000110100011000000 * 2^6
阶为6,偏置127即133,占8位为:1000 0101
步骤④:根据数值的正负定义符号位
由于数值为正,所以符号位S为0。
步骤⑤:根据知识点一进行数值组装
![]()
此二进制值为98.20458984375,意味着在二进制表示和存储阶段即有精度损失了。
4.精度相关话题
4.1. 存在一个浮点常量,其他浮点值加上它之后小数点后值不变吗?
不存在,在计算机中浮点值相加并不是简单的整数+整数,小数+小数,其结果在转为二进制存储阶段也有可能会继续损失精度。
有些情况下我们可能需要把浮点值偏置处理为某个范围再继续进行应用,这种处理很可能会带来精度损失。
4.2. 尽量减少浮点数据的处理和运算
尽量减少浮点数据的处理和运算,每次运算都可能会损失精度,在有些算法计算中尽量采用逻辑清晰简便的处理过程,减少精度损失。如求向量夹角,需要尽量简化运算过程,以保持较高的结果精度。想想为什么公式推导很重要?化繁为简!便于应用。
4.3. 尽量减少溢出运算
每次溢出都会损失精度,在数学类的计算或几何算法中是一个绕不开的话题。后续博主可能会开一个系列讲几何算法中提高精度的一些经验措施。
4.4. 关注浮点值的标识范围
关注浮点值的标识范围,避免超出范围的计算处理,如果可能超出范围则用更高范围和精度的类型或采用其他处理办法。
想想为什么4字节float表示范围约为![]() ?
?
我们看看阶码,阶码为8位,由阶偏置127得到,这样阶最大为
也就是上述范围。
5. 参考文章
1、二进制转换网站:
IEEE 754 浮点数转换 - 锤子在线工具
2、浮点数的二进制表示
浮点数的二进制表示_浮点 二进制-CSDN博客
3、大白话说float型的精度和范围
大白话说float型的精度和范围_float范围值的大小-CSDN博客
4、 float的精度和取值范围
float的精度和取值范围_float精度-CSDN博客
5、浅谈C/C++的浮点数在内存中的存储方式
http://t.csdnimg.cn/9xzXI
浅谈C/C++的浮点数在内存中的存储方式-CSDN博客
6、C++/C--浮点型数据的二进制表示及其内存存储形式
C++/C--浮点型数据的二进制表示及其内存存储形式_c++输出浮点数的二进制形式-CSDN博客
7、深入理解浮点数:阶码为什么要加上偏移量等4个问题
深入理解浮点数:阶码为什么要加上偏移量等4个问题_阶码为什么加127-CSDN博客
8、计算机组成原理:浮点数的加、减、乘、除运算(含实例完整运算)
计算机组成原理:浮点数的加、减、乘、除运算(含实例完整运算)_浮点数运算-CSDN博客
相关文章:

关于float浮点值二进制存储和运算精度损失的话题
1.前言 浮点值的存储、运算都可能会带来精度损失,了解精度损失背后的机制原因方便我们更好的了解什么情况下会发生精度损失、什么情况下精度损失较大,以及思考怎么避免或减少精度损失。 2.知识点 (1)IEEE 754标准 EEE 754标准…...

python爬虫学习记录-请求模块urllib3
(文章内容仅作学习交流使用) urllib3是一个功能强大、条理清晰,用于HTTP客户端的第三方模块 urllib3-发送网络请求 使用urllib3发送网络请求时,需要先创建PoolManager对象,并使用该对象的request方法发送请求&#…...

谷粒商城实战笔记-133~135-城业务-商品上架-远程上架接口
文章目录 一,谷粒商城实战笔记-133-城业务-商品上架-远程上架接口1,开发目标2,详细设计2.1,提前建立索引2.2,构造批量操作请求参数2.3,使用HighLevelClient调用bulk请求保存数据 二,134-商城业务…...

【React】详解 App.js 文件
文章目录 一、App.js文件的基本结构1. 引入必要的模块2. 定义根组件3. 导出根组件 二、App.js文件的详细解析1. 函数组件与类组件函数组件类组件 2. 使用CSS模块3. 组织子组件4. 管理组件状态使用useState钩子使用state对象 三、App.js文件的最佳实践1. 保持组件的简洁和模块化…...

【ML】self-supervised Learning for speech and Image
【ML】self-supervised Learning for speech and Image 1. self-supervised Learning for speech and Image1.1 自监督学习在语音处理领域的方法及其特点1.2 自监督学习在图像处理领域的方法及其特点 2. Predictive Approach2.1 特点2.2 适用场景 3. contrastive Learning4. 语…...
)
青岛实训day24(8/8)
一.Python环境准备 1.查看有没有python3 yum list installed |grep python yum list |grep python3 最新安装3.12可以使用源码安装 2.下载安装python3 yum -y install python3 3.查看版本 [rootpython ~]# python3 --version Python 3.6.8 4.进入编辑 [r…...
第四十五天 | 101. 孤岛的总面积、102. 沉没孤岛、103. 水流问题、104. 建造最大岛屿)
*算法训练(leetcode)第四十五天 | 101. 孤岛的总面积、102. 沉没孤岛、103. 水流问题、104. 建造最大岛屿
刷题记录 101. 孤岛的总面积DFSBFS 102. 沉没孤岛DFSBFS *103. 水流问题*104. 建造最大岛屿 101. 孤岛的总面积 题目地址 本题要求不与矩阵边缘相连的孤岛的总面积。先将与四个边缘相连的岛屿变为海洋,再统计剩余的孤岛的总面积。无需再标识访问过的结点ÿ…...
)
设计模式 由浅入深(待完结)
一、设计模式是什么? 设计模式是指在软件开发中,经过验证的,用于解决在特定环境下,重复出现的,特定问题的解决方案。 二、设计模式有哪些? 1. 观察者模式 定义对象间的一种一对多(变化&#x…...
645、最大二叉树)
(第34天)645、最大二叉树
目录 645、最大二叉树题目描述思路代码 645、最大二叉树 题目描述 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大…...

Python知识点:如何使用Paramiko进行SSH连接与操作
使用Paramiko进行SSH连接与操作可以分为以下几个步骤: 安装Paramiko: 首先需要安装Paramiko库,可以使用pip进行安装: pip install paramiko建立SSH连接: 使用Paramiko连接远程服务器,需要提供服务器的地址、…...

代码随想录算法训练营第六天(一)|242.有效的字母异位词
LeetCode 242 有效的字母异位词 题目: 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 示例 1: 输入: s "anagram&q…...

数据结构 | 考研代码题之顺序表 | 1 查找L中值为e的数据元素若找到则返回其下标,若找不到则返回-1
文章目录 1 题目2 题解 1 题目 假设有一个顺序表 L,其存储的所有数据元素均为不重复的正数,查找L中值为e的数据元素,若找到则返回其下标,若找不到则返回-1。 2 题解 C语言代码: /*假设有一个顺序表 L,其…...

RLVF:避免过度泛化地从口头反馈中学习
人工智能咨询培训老师叶梓 转载标明出处 大模型在不同行业和个人中的广泛应用要求模型能够根据具体的用户反馈进行调整或定制,以满足细微的要求和偏好。虽然通过高层次的口头反馈来指定模型调整非常方便,例如“在给老板起草电子邮件时不要使用表情符号”…...

设计原则与思想-从项目实战中学习设计模式
文章目录 开源项目通过剖析Java JDK源码学习灵活应用设计模式1. 单例模式(Singleton Pattern)示例:`java.lang.Runtime`2. 工厂模式(Factory Pattern)示例:`java.util.Date`3. 观察者模式(Observer Pattern)示例:`java.util.Observable` 和 `java.util.Observer`4. 适…...

python中的类属性、实例属性、类方法、实例方法和静态方法
1. 类属性(类变量)和实例属性(实例变量) 在python中,类中的属性就是定义在类中的变量,简称成员变量;类中的行为就是定义在类中的方法,简称成员方法。成员变量又可分为类变量和实例变量,或者分为类属性和实例属性。成员…...

A股继续底部震荡,探底是否能成功?
真心的给股民朋友提个醒,不管你胆大还是胆怯,盘面上出现了1个反常信号,一起来看看: 1、今天两市低开高走,开始筑底了,任何一个主力,都是在无人问津的熊市布局,而在人声鼎沸的牛市离场…...

NPDP考前怎么复习?NPDP200问PDF版来啦~
距离NPDP下半年考试还有4个月的时间,现在正是备考的黄金期。 以下复习建议~ 01.制定详细计划 首先,根据考试大纲,可以将内容划分为几个模块,如新产品开发流程、市场研究、产品规划等,并为每个模块设定学习目标和时间…...

ajax图书管理项目
bootstrap弹框 不离开当前页面,显示单独内容,让用户操作 功能:不离开当前页面,显示单独内容,供用户操作步骤: 1.引入bootstrap.css和bootstrap.js …...
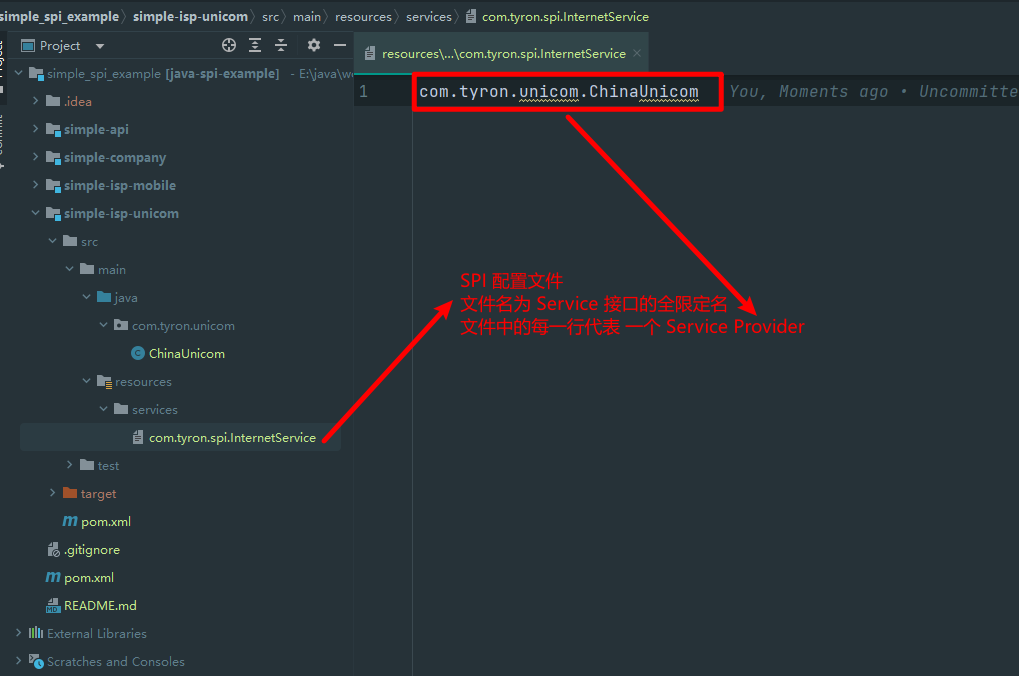
深入理解 Java SPI - 概念、原理、应用
零、前言 在当今互联网时代,应用程序越来越复杂,对于我们开发人员来说,如何实现高效的组件化和模块化已经成为了一个重要的问题。而 Java SPI(Service Provider Interface)机制,作为一种基于接口的服务发现…...

JavaScript - 判断数组中是否包含某个的元素的几种方式
目录 1. 使用 includes 方法 2. 使用 indexOf 方法 3. 使用 find 方法 4. 使用 some 方法 5. 使用 filter 方法 6. 使用 every 方法 应该算是前端开发过程中比较常用的基本操作,话不多说,看代码。 1. 使…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
