2024/8/8训练
A - 无线网络整点栅格统计
题目链接
算法:模拟
题目大意
给你一个n*m的网格,然后输出每一个点作为顶点能构成的正方形数量(可以为斜正方形).
算法思路
本身题目数据是很小的,可以通过n^2的时间复杂度枚举每一个顶点,然后再通过n平方的时间复杂度枚举出另一个对角顶点,判断剩下的两个点是否在网格里面即可.这样的话时间复杂度是n的四次方时间复杂度了,可以通过.
我们可以知道当以A为顶点的斜正方形一定可以被过A的正正方形包围,那么我们每个店只需要求出过这个点所能构成的正正方形数量即可.
至于如何求每个点构成的正正方形数量可以根据个人理解来求.
我的思路是:我们可以通过记录A点左边,上边,斜左上角,本身的正正方形数量,然后这样过A点的正正方形数量就是四个之和.
代码
#include<bits/stdc++.h>
#define ll long long
const int N = 1e5+7;
int dx[]= {1,-1,0,0,1,1,-1,-1};
int dy[]= {0,0,1,-1,1,-1,1,-1};
using namespace std;
struct Node {//自身 左边 上边//左上角int ct,lt,fr;int lf;
};
Node a[107][107];
int n,m;
int ce(int x,int y) {return min(n+1-x,m+1-y);
}
int celf(int x,int y) {return min(x-1,m+1-1)*min(y-1,n+1-1);
}
int ti[107][107];
int tj[107][107];
void slove() {for(int i=1; i<=100; ++i) {ti[0][i]=-2;tj[i][0]=-2;}cin>>n>>m;for(int i=1; i<=(ll)ceil(1.0*(n+1)/2); ++i) {for(int j=1; j<=(ll)ceil(1.0*(m+1)/2); ++j) {a[i][j].ct=ce(i,j);if(i<=m+1) {ti[i][j]=ti[i-1][j]+1;if(i!=1) a[i][j].fr=a[i-1][j].ct+max(0,(a[i-1][j].fr+-ti[i][j]));} else {//需要去掉刚好到i-1的情况a[i][j].fr=a[i-1][j].fr;}if(j<=n+1) {tj[i][j]=tj[i][j-1]+1;if(j!=1) a[i][j].lt=a[i][j-1].ct+max(0,(a[i][j-1].lt+-tj[i][j]));} else {//需要去掉刚好到j-1的情况a[i][j].lt=a[i][j-1].lt;}a[i][j].lf=celf(i,j);}}for(int i=1; i<=(ll)ceil(1.0*(n+1)/2); ++i) {for(int j=1; j<=(ll)ceil(1.0*(m+1)/2); ++j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}if((m+1)%2==0) {for(int j=(ll)ceil(1.0*(m+1)/2); j>=1; --j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}} else {for(int j=(ll)ceil(1.0*(m+1)/2)-1; j>=1; --j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}}cout<<endl;}if((n+1)%2==0) {for(int i=(ll)ceil(1.0*(n+1)/2); i>=1; --i) {for(int j=1; j<=(ll)ceil(1.0*(m+1)/2); ++j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}if((m+1)%2==0) {for(int j=(ll)ceil(1.0*(m+1)/2); j>=1; --j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}} else {for(int j=(ll)ceil(1.0*(m+1)/2)-1; j>=1; --j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}}cout<<endl;}} else {for(int i=(ll)ceil(1.0*(n+1)/2)-1; i>=1; --i) {for(int j=1; j<=(ll)ceil(1.0*(m+1)/2); ++j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}if((m+1)%2==0) {for(int j=(ll)ceil(1.0*(m+1)/2); j>=1; --j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}} else {for(int j=(ll)ceil(1.0*(m+1)/2)-1; j>=1; --j) {cout<<a[i][j].ct+a[i][j].fr+a[i][j].lt+a[i][j].lf<<" ";}}cout<<endl;}}return;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t = 1;
// cin>>t;while(t--) {slove();cout<<endl;}return 0;
}C. Liar
题目链接
算法:思维
题目大意
有n个数,这些个数的总和为s,这些数有真有假,输出最多有多少个数是真的
算法思路
因为当这个数为假的时候,我们可以把这个数设为无穷数,那么当n个数都为真无法满足总和为s的情况,我们可以让前n-1个数都为真,然后通过最后一个数进行调节,满足n个数的总和为s的情况
代码
#include<bits/stdc++.h>
#define ll long long
const int N = 1e5+7;
int dx[]= {1,-1,0,0,1,1,-1,-1};
int dy[]= {0,0,1,-1,1,-1,1,-1};
using namespace std;
ll a[N];
void slove() {ll n,s;cin>>n>>s;for(int i=1; i<=n; ++i) cin>>a[i];sort(a+1,a+n+1);ll ans = 0;for(int i=1; i<=n; ++i) {ans+=a[i];}if(ans==s) {cout<<n;return;}cout<<n-1;
}
int main() {int t = 1;
// cin>>t;while(t--) {slove();cout<<endl;}return 0;
}Magic LCM
题目链接
算法:数学+模拟+贪心
题目大意
给你一个长度为n的数组,然后你可以进行无数次操作:选择两个不同的数(x,y),设x为gcd(x,y),y为lcm(x,y).
求出最后这个数组之和的最大值.
算法思路
对于两个数进行gcd和lcm赋值,其实gcd就是公共因子,lcm就是公共因子不同的因子.
而且因子和因子之间互不打扰.
那么我们就可以把数组里面的每一个数进行拆解,拆解成质因子,依次求出进行操作以后的最大值.
又因为操作就是将公共因子乘不同的因子,那么我们可以让质因子个数多的先提供,求出一个当前的最大值.
比如:9 6 4 27 10 12这个数组
9->33
6->23
4->22
27->333
10->25
12->223
那么我们可以先让4提供两个2,27提供三个3,10提供一个5,这样组成540.
剩下的数
33
23
2
22*3
注意,质因子之间相互独立,所以不用在意是具体是谁提供的
我们继续两个2,两个3组成36
一个2.一个3
组成6
一个2.一个3
组成6
这样把所有的质因子都用掉以后
还剩下两个数,这两个数就是1
#include<bits/stdc++.h>
#define ll long long
const int N = 1e6+7;
const int M = 998244353;
int dx[]= {1,-1,0,0,1,1,-1,-1};
int dy[]= {0,0,1,-1,1,-1,1,-1};
using namespace std;
struct Node {map<int,ll> mp;set<int> st;
};
Node a[N];
priority_queue<ll, vector<ll>, less<ll>> q[N];
set<int> tst;
ll q_pow(ll n,ll x) {ll sum=1;while(x) {if(x&1) sum*=n;x>>=1;n*=n;n%=M;sum%=M;}sum%=M;return sum;
}
void slove() {ll n;cin>>n;for(int i=1,t; i<=n; ++i) {cin>>t;for(auto &v:a[t].st) {tst.insert(v);q[v].push(a[t].mp[v]);}}ll ans = 0;int sz = 0;int flag = 0;while(1) {flag = 0;ll tans = 1;for(auto it = tst.begin(); it != tst.end();) {if(q[*it].empty()) {it = tst.erase(it);} else {flag = 1;ll t = q_pow(*it,q[*it].top());q[*it].pop();tans*=t;tans%=M;++it;}}ans += tans;ans%=M;sz++;if(flag == 0) break;}cout<<ans+n-sz;return;
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);a[1].mp[1]=1;for(int i=2; i<=1e6; ++i) {int flag = 0;for(int j=2; j*j<=i; ++j) {if(i%j==0) {flag = 1;int t = i/j;for(auto &v:a[t].st) {a[i].mp[v]+=a[t].mp[v];a[i].st.insert(v);}a[i].mp[j]++;a[i].st.insert(j);break;}}if(flag == 0) {a[i].mp[i]++;a[i].st.insert(i);}}// int mx = 0;
// for(int i=1;i<=1e6;++i) {
// mx = max(mx,(int)a[i].st.size());
// }
// cout<<mx;int t = 1;cin>>t;while(t--) {slove();cout<<endl;}return 0;
}
这个代码部分main里面对如何在nlogn的时间复杂度求出1-n里面每个数分别有哪些因子可以重点看一下.
相关文章:

2024/8/8训练
A - 无线网络整点栅格统计 题目链接 算法:模拟 题目大意 给你一个n*m的网格,然后输出每一个点作为顶点能构成的正方形数量(可以为斜正方形). 算法思路 本身题目数据是很小的,可以通过n^2的时间复杂度枚举每一个顶点,然后再通过n平方的时间复杂度枚举出另一个对角顶点,判断…...

项目的小结
项目场景: 作业的发布,打回 。 学生端做作业 由作业的state来确定作业是否上交,批改,打回作业。 实体类的建立,还有各种成员变量的设计要满足需求 问题描述 问题: 在进行上传作业后,老师端…...

【目标检测实验系列】YOLOv5高效涨点:基于NAMAttention规范化注意力模块,调整权重因子关注有效特征(文内附源码)
1. 文章主要内容 本篇博客主要涉及规范化注意力机制,融合到YOLOv5(v6.1版本,去掉了Focus模块)模型中,通过惩罚机制,调整特征权重因子,使模型更加关注有效特征,助力模型涨点。 2. 简要概括 论文地址&#x…...

LSPatch制作内置模块应用软件无需root 教你制作内置应用
前言 LSPatch功能非常强大,它是一款基于LSPosed核心的免Root Xposed框架软件。这意味着用户无需进行手机root操作,即可轻松植入内置Xposed模块,享受更多定制化的功能和体验,比如微某内置模块版等,这为那些不想root手机…...

Java设计模式七大原则
本篇为七大原则概述,后面会有每个原则的介绍,喜欢的朋友可以蹲一下哦!!!! Java设计模式的七大原则一般是指“面向对象设计原则”,这些原则有助于在设计软件系统时提高代码的可维护性、可扩展性和…...

Copy as cURL 字段含义
当前端在开发过程中,遇到接口错误反馈给后端人员时,一般在此接口处右键复制为cURL。 格式如下: curl https://xxx.xxx.cn/xxx/xxx/management/record/list \-H accept: application/json, text/plain, */* \-H accept-language: zh-CN,zh;q0…...

mysql更改密码后,若依 后端启动不了解决方案
我原先的mysql 密码是 数字字符串 我想改成000 纯数字 改完之后,连接的数据库的代码 也更改后 ,后端启动不了 因为原先 密码数字字符串 不需要用引号" " 括起来 我改成纯数字 需要用 " " 括起来 如下图 然后就可以运行成功了...

Redis--缓存击穿、缓存穿透、缓存雪崩
缓存击穿 什么是缓存击穿呢? 在高并发的场景下,一个热点的缓存数据在redis中突然失效(过期或被删除时,所有的读请求都会直接落在数据库上,导致数据库瞬间压力剧增,严重时可能会造成数据库宕机。这种情况就是所谓的“缓存击穿”。(…...

10个理由告诉你,为什么鸿蒙是下一个职业风口!
在当今科技飞速发展的时代,新的技术和趋势不断涌现,为人们带来了前所未有的机遇和挑战。鸿蒙操作系统作为我国自主研发的创新成果,正逐渐成为科技领域的焦点,被认为是下一个职业风口。 10个理由告诉你,为什么鸿蒙是下一…...

Gitlab仓库的权限分配以及如何查看自己的权限
在GitLab中,权限分配和查看自己的权限可以通过以下步骤进行: ### 1. 查看自己的权限 要查看你在某个GitLab项目中的权限,可以按照以下步骤操作: 1. 登录到GitLab。 2. 进入你想查看权限的项目页面。 3. 在左侧菜单中,…...
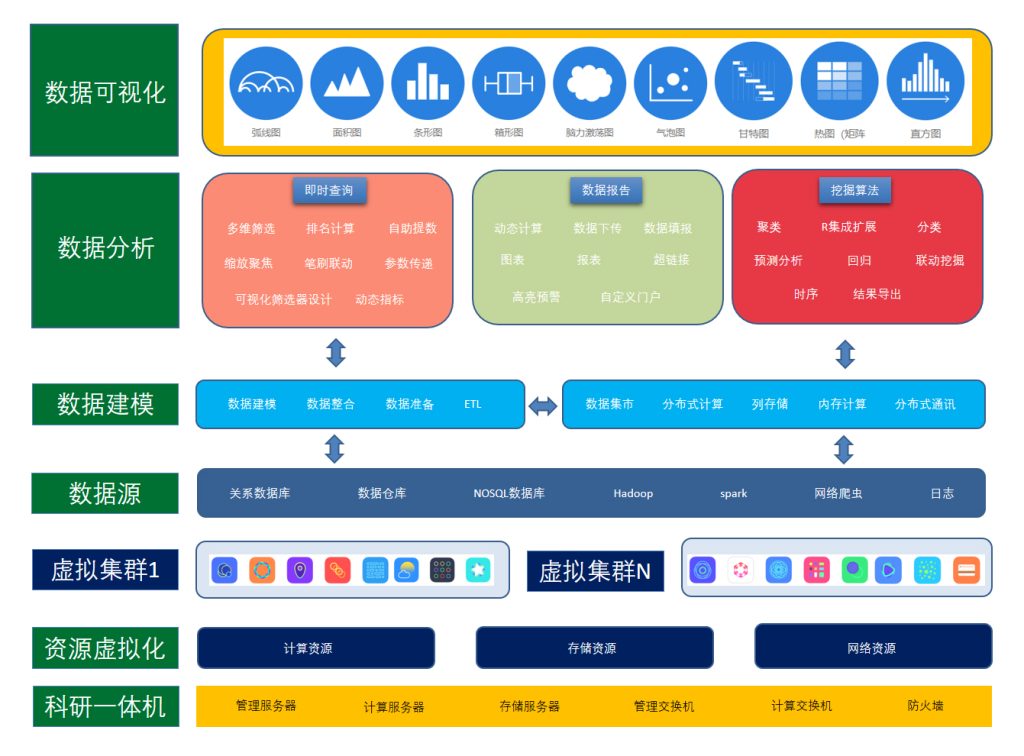
职业本科大数据实训室
一、职业本科大数据实训室建设背景 在数字化浪潮汹涌澎湃的今天,大数据已跃升为引领社会进步和经济发展的新引擎。随着《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》的深入实施,数字化转型作为国家战略的重要组成部分&…...

【密码学】网络攻击类型:窃听攻击、假冒攻击、欺骗攻击和重放攻击
一、窃听攻击、假冒攻击、欺骗攻击和重放攻击的定义 这些攻击从名字中就大概能知道他们的攻击原理,我就不赘述了,直接用一个表格来一次性介绍四种攻击方式。 攻击类型攻击原理窃听攻击攻击者监听网络中的数据传输以获取敏感信息。示例:在未加…...

探索WebKit的奥秘:塑造高效、兼容的现代网页应用
探索WebKit的奥秘:塑造高效、兼容的现代网页应用 在数字时代的洪流中,网页应用已成为连接用户与信息的桥梁,其性能、兼容性和用户体验直接决定了产品的成败。WebKit,作为众多现代浏览器背后的核心渲染引擎,承载着将HT…...

2-52 基于matlab局部信息的模糊C均值聚类算法(FLICM)
基于matlab局部信息的模糊C均值聚类算法(FLICM),是在FCM聚类算法的基础上结合了图像的邻域信息,有更好的鲁棒性。程序已调通,可直接运行。 2-52 局部信息的模糊C均值聚类算法 - 小红书 (xiaohongshu.com)...

JAVASE
1.泛型 泛型指类型参数化, 在定义期间,不知道调用时会使用什么类型,就可以添加泛型形参,在使用时传入实参固定类型即可。 泛型类: 泛型应用在类上。 一般用在类名后,用尖括号括起来。用大写字母作为泛型参…...

SpringBoot学习之EasyExcel解析合并单元格(三十九)
本解析主要采用反射来修改EasyExcel 返回的默认数据结构实现。 一、待解析表格 二、依赖 全部pom.xml文件如下,仅作参考: <project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLo…...

【Kimi学习笔记】C/C++、C#、Java 和 Python
C/C、C#、Java 和 Python 是几种流行的编程语言,它们在设计哲学、用途、语法和运行机制上有所不同。下面我会类比 Java 来解释这些语言的区别: 1. C/C: 类比于 Java,C/C 是一种更接近硬件的低级语言,提供了更多的控制…...

基于贪心算法的路径优化
贪心算法原理 贪心算法的核心原理是在每一步选择中都采取在当前看来最好的选择,以期达到全局最优解。 这种算法不追求整体最优解,而是通过局部最优的选择逐步逼近全局最优解。贪心算法的关键在于构造合适的贪心策略,这种策略需要满足两个基本要素:贪婪选择属性和最优子…...

谷粒商城实战笔记-140-商城业务-nginx-搭建域名访问环境二(负载均衡到网关)
文章目录 一,通过域名访问商城架构设计1,为什么nginx要将请求转发给网关2,架构设计 二,配置1,nginx配置1.1 nginx.conf1.2 gulimall.conf1.3 配置原理 2,网关配置 三,记录2个问题1,网…...

【Android Studio】 创建第一个Android应用HelloWorld
文章目录 创建项目查看AndroidManifest.xml(清单)查看MainActivity.java(Activity)查看activity_main.xml(布局) 创建项目 查看AndroidManifest.xml(清单) 查看MainActivity.java(Activity&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
