算法学习day31(动态规划)
一、比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
输入:n = 2 输出:[0,1,1] 解释:0 --> 0 1 --> 1 2 --> 10
思路一: 如果是偶数的话,1的个数和它的一半是相同的;如果是奇数的话,1的个数等于它前面那个偶数的个数+1
代码:
int countBits(int num) {int[] res=new int[num+1]result[0] = 0;for(int i = 1; i <= num; i++){if(i%2==0)res[i]=res[i/2];else res[i]=res[i-1]+1;}return result;}
思路二:遇到一个数,想办法把它拆成 最靠近它的2的幂 和另一个数
eg:7拆成4和3 4中1的个数有1个,3中1的个数有2个 所以res[7]=res[4]+res[3]
如果遇到2的幂次,dp[i]=1;
代码:
public int[] countBits(int n) {int[] dp = new int[n + 1];dp[0] = 0;int x = 1;for (int i = 1; i <= n; i++) {// 如果是2的幂,只有最高位为1if (i == x) {dp[i] = 1;x *= 2;} else {// 如果不是2的幂,则为取模最高位后的值+1// 例如 5 % 4 = 1, 那么就是4+1也就是 101;也就是1+dp[1]; int mod = i % (x / 2);dp[i] = 1 + dp[mod];//1代表的是2的幂,dp[mod]代表的是剩下的那个数的1的值}}return dp;}二、打家劫舍/打家劫舍II(二刷 dp)
题意:小偷要偷窃,相邻房屋是不能偷窃的,否则就会发出报警信号。给定一个数组nums,表示每个房间的价值,第一个房屋和最后一个房屋是相邻的,给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
思路:
因为房屋是相邻的,所以要破除这个环,那么应该如何破除?因为首尾是相连的,所以我们只需要考虑两种情况:偷首就不能偷尾;偷尾就不能偷首
那我们就把两种情况分别可以偷窃到的最高金额计算出来,比较之后返回。
那么如何计算偷窃道德最高金额?动态规划。
一间屋子可以偷也可以不偷,偷的话dp[i]=dp[i-2]+nums[i];不偷的话:dp[i]=dp[i-1]
dp[i]:偷窃到第i间房子所偷窃的最大价值
递推公式:dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
初始化:dp[0]=nums[0],dp[1]=Math.max(nums[0],nums[1]);
遍历顺序:从i=2开始
代码:
class Solution {public int rob(int[] nums) {if(nums.length<=1)return nums[0];//如何破环int part1=getMax(nums,0,nums.length-2);int part2=getMax(nums,1,nums.length-1);return Math.max(part1,part2);}public int getMax(int[] nums,int left,int right){if(right==left)return nums[left];int[] dp=new int[right-left+1];dp[0]=nums[left];dp[1]=Math.max(nums[left],nums[left+1]);for(int i=left+2;i<=right;i++){dp[i-left]=Math.max(dp[i-2-left]+nums[i],dp[i-1-left]);}return Math.max(dp[dp.length-1],dp[dp.length-2]);}
}三、两个键的键盘(dp)
最初记事本上只有一个字符 'A' 。你每次可以对这个记事本进行两种操作:
Copy All(复制全部):复制这个记事本中的所有字符(不允许仅复制部分字符)。Paste(粘贴):粘贴 上一次 复制的字符。
给你一个数字 n ,你需要使用最少的操作次数,在记事本上输出 恰好 n 个 'A' 。返回能够打印出 n 个 'A' 的最少操作次数。
思路:
如何才可以得到n个‘A’?可以根据因数来做。
eg:n=12; 可以是6个A CopyAll->Paste之后得到12个A
也可以是3个A CopyAll->Paste3次后得到12个A
还可以是2个A CopyAll->Paste5次后得到12个A
如果是质数的话,那么操作的次数就是它本身,需要CopyAll+Paste(n-1)次
所以就是在它的因数里面找最小操作次数。双循环
代码:
class Solution {public int minSteps(int n) {//dp[i]的定义:打印出i个A字符需要的操作次数int[] dp=new int[n+1];//dp初始化dp[1]=0;//遍历数组for(int i=2;i<=n;i++){dp[i]=i;for(int j=2;j<=Math.sqrt(i);j++){if(i%j==0){dp[i]=Math.min(dp[i],dp[j]+i/j);dp[i]=Math.min(dp[i],dp[i/j]+j);}}}return dp[n];}
}四、解码方法
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
"1" -> 'A' "2" -> 'B' "25" -> 'Y' "26" -> 'Z'
然而,在 解码 已编码的消息时,你意识到有许多不同的方式来解码,因为有些编码被包含在其它编码当中("2" 和 "5" 与 "25")。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。如果没有合法的方式解码整个字符串,返回 0。
输入:s = "226" 输出:3 解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
思路:这道题是爬楼梯类似。但是比爬楼梯要多个决定条件。
给定一串字符串。
如果该数字不等于0,那么就可以只切割该字符,此时dp[i+1]=dp[i]; 和爬楼梯从下一层爬到该层一样;
在上一个条件的基础上,如果该数字可以和前一个数字组成一个合法的字符(>=10&&<=26),那么就可以从下两层爬到该层(一次爬两个)。此时dp[i+1]+=dp[i-1];
动态规划五部曲:
1.dp[i]:代表的含义是:字符串中以i-1为结尾的字串的切割方法有多少种。dp.length=s.length()+1
2.递推公式:
2.1如果和上一个数字无法组成合法的大写字母:dp[i+1]=dp[i];
2.2 如果和上一个数字可以组成合法的大写字母:dp[i+1]=dp[i]+dp[i-1]
3.初始化:dp[0]=dp[1]=1; 默认空串也有一种切割方式。
eg:226。遍历到index=1的时候,可以组成一个合法的大写字母。dp[i+1]=dp[i]+dp[i-1]。这里的dp[i-1]就代表着22
代码:
class Solution {public int numDecodings(String s) {int size=s.length();int[] dp=new int[size+1];dp[0]=1;//初始化 dp[1]=1;//dp[i]表示的是字符串中以(i-1)为结尾的字串 有多少种切割方式if(s.charAt(0)=='0')return 0;for(int i=1;i<size;i++){char ch1=s.charAt(i);if(ch1-'0'!=0){dp[i+1]+=dp[i];}char ch2=s.charAt(i-1);//如果这两个数字可以组成一个有效的大写字母if((ch2-'0')*10+(ch1-'0')>=10&&(ch2-'0')*10+(ch1-'0')<=26){dp[i+1]+=dp[i-1];}}return dp[size];}
}相关文章:
)
算法学习day31(动态规划)
一、比特位计数 给你一个整数 n ,对于 0 < i < n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n 1 的数组 ans 作为答案。 输入:n 2 输出:[0,1,1] 解释:0 --> 0 1 --> 1 2 -…...

嵌入式学Day25---Linux软件编程---线程间通信
目录 编辑 一、线程的分离属性 1.1.什么是分离属性 1.2.分离属性相关函数接口 1.初始化线程属性-pthread_attr_init() 2.销毁线程属性-pthread_attr_destory() 3.设置线程属性-pthread_setdetachstate() 1.3.注意 二、互斥锁 2.1.资源 2.2.互斥锁 1.什么是互斥锁 2.互…...

【实现100个unity特效之17】在unity中使用shader和ShaderGraph分别实现模糊特定层,高斯模糊效果
最终效果 Unity通过Shader来模糊场景画面 参考:【游戏开发小技】Unity通过UI全屏图来模糊场景画面(Shader | 模糊 | 滤镜 | Blur) ShaderGraph实现图片的高斯模糊 参考:【游戏开发实战】Unity ShaderGraph实现图片的高斯模糊效…...

Unity补完计划 之 SpriteEditer Multiple
本文仅作笔记学习和分享,不用做任何商业用途 本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 1. SpriteEditer Multiple Automatic slicing - Unity 手册 这是用于裁剪图集的模式 应用之后精灵编辑器会看到Slice亮…...

C++ IOStream
IOStream 类流特性 不可赋值和复制缓冲重载了<< >> 状态位 示例 状态位操作函数coutcin getget(s,n)/get(s,n,d):getline otherif(!fs)/while(cin) operator void*()与 operator!()代码示例 File Stream open 函数 文件打开方式 文件读写 读写接口 一次读一个字符…...

2024/8/8训练
A - 无线网络整点栅格统计 题目链接 算法:模拟 题目大意 给你一个n*m的网格,然后输出每一个点作为顶点能构成的正方形数量(可以为斜正方形). 算法思路 本身题目数据是很小的,可以通过n^2的时间复杂度枚举每一个顶点,然后再通过n平方的时间复杂度枚举出另一个对角顶点,判断…...

项目的小结
项目场景: 作业的发布,打回 。 学生端做作业 由作业的state来确定作业是否上交,批改,打回作业。 实体类的建立,还有各种成员变量的设计要满足需求 问题描述 问题: 在进行上传作业后,老师端…...

【目标检测实验系列】YOLOv5高效涨点:基于NAMAttention规范化注意力模块,调整权重因子关注有效特征(文内附源码)
1. 文章主要内容 本篇博客主要涉及规范化注意力机制,融合到YOLOv5(v6.1版本,去掉了Focus模块)模型中,通过惩罚机制,调整特征权重因子,使模型更加关注有效特征,助力模型涨点。 2. 简要概括 论文地址&#x…...

LSPatch制作内置模块应用软件无需root 教你制作内置应用
前言 LSPatch功能非常强大,它是一款基于LSPosed核心的免Root Xposed框架软件。这意味着用户无需进行手机root操作,即可轻松植入内置Xposed模块,享受更多定制化的功能和体验,比如微某内置模块版等,这为那些不想root手机…...

Java设计模式七大原则
本篇为七大原则概述,后面会有每个原则的介绍,喜欢的朋友可以蹲一下哦!!!! Java设计模式的七大原则一般是指“面向对象设计原则”,这些原则有助于在设计软件系统时提高代码的可维护性、可扩展性和…...

Copy as cURL 字段含义
当前端在开发过程中,遇到接口错误反馈给后端人员时,一般在此接口处右键复制为cURL。 格式如下: curl https://xxx.xxx.cn/xxx/xxx/management/record/list \-H accept: application/json, text/plain, */* \-H accept-language: zh-CN,zh;q0…...

mysql更改密码后,若依 后端启动不了解决方案
我原先的mysql 密码是 数字字符串 我想改成000 纯数字 改完之后,连接的数据库的代码 也更改后 ,后端启动不了 因为原先 密码数字字符串 不需要用引号" " 括起来 我改成纯数字 需要用 " " 括起来 如下图 然后就可以运行成功了...

Redis--缓存击穿、缓存穿透、缓存雪崩
缓存击穿 什么是缓存击穿呢? 在高并发的场景下,一个热点的缓存数据在redis中突然失效(过期或被删除时,所有的读请求都会直接落在数据库上,导致数据库瞬间压力剧增,严重时可能会造成数据库宕机。这种情况就是所谓的“缓存击穿”。(…...

10个理由告诉你,为什么鸿蒙是下一个职业风口!
在当今科技飞速发展的时代,新的技术和趋势不断涌现,为人们带来了前所未有的机遇和挑战。鸿蒙操作系统作为我国自主研发的创新成果,正逐渐成为科技领域的焦点,被认为是下一个职业风口。 10个理由告诉你,为什么鸿蒙是下一…...

Gitlab仓库的权限分配以及如何查看自己的权限
在GitLab中,权限分配和查看自己的权限可以通过以下步骤进行: ### 1. 查看自己的权限 要查看你在某个GitLab项目中的权限,可以按照以下步骤操作: 1. 登录到GitLab。 2. 进入你想查看权限的项目页面。 3. 在左侧菜单中,…...
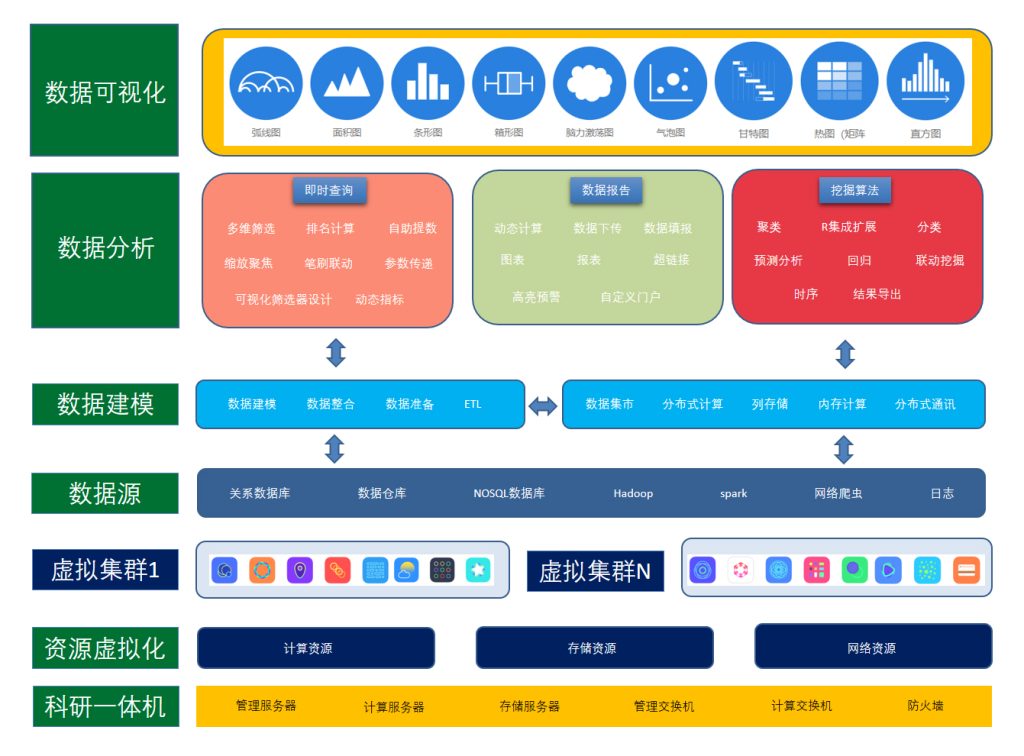
职业本科大数据实训室
一、职业本科大数据实训室建设背景 在数字化浪潮汹涌澎湃的今天,大数据已跃升为引领社会进步和经济发展的新引擎。随着《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》的深入实施,数字化转型作为国家战略的重要组成部分&…...

【密码学】网络攻击类型:窃听攻击、假冒攻击、欺骗攻击和重放攻击
一、窃听攻击、假冒攻击、欺骗攻击和重放攻击的定义 这些攻击从名字中就大概能知道他们的攻击原理,我就不赘述了,直接用一个表格来一次性介绍四种攻击方式。 攻击类型攻击原理窃听攻击攻击者监听网络中的数据传输以获取敏感信息。示例:在未加…...

探索WebKit的奥秘:塑造高效、兼容的现代网页应用
探索WebKit的奥秘:塑造高效、兼容的现代网页应用 在数字时代的洪流中,网页应用已成为连接用户与信息的桥梁,其性能、兼容性和用户体验直接决定了产品的成败。WebKit,作为众多现代浏览器背后的核心渲染引擎,承载着将HT…...

2-52 基于matlab局部信息的模糊C均值聚类算法(FLICM)
基于matlab局部信息的模糊C均值聚类算法(FLICM),是在FCM聚类算法的基础上结合了图像的邻域信息,有更好的鲁棒性。程序已调通,可直接运行。 2-52 局部信息的模糊C均值聚类算法 - 小红书 (xiaohongshu.com)...

JAVASE
1.泛型 泛型指类型参数化, 在定义期间,不知道调用时会使用什么类型,就可以添加泛型形参,在使用时传入实参固定类型即可。 泛型类: 泛型应用在类上。 一般用在类名后,用尖括号括起来。用大写字母作为泛型参…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
