《算法竞赛进阶指南》0x23剪枝
剪枝,就是减少搜索树的规模、尽可能排除搜索书中不必要的分支的一种手段。形象地看,就好像剪掉了搜索树的枝条,故被称为“剪枝”。在深度优先搜索中,有以下常见的剪枝方法。
1.优化搜索顺序
在一些搜索问题中,搜索树的各个层次、各个分支之间的顺序不是固定的。不同的搜索顺序会产生不同的搜索树形态,其规模大小也相差甚远。
(1).在小猫爬山问题中,把小猫按照重量递减的顺序进行搜索;
(2).在数独问题中,优先搜索“能填的合法数字”最少的位置。
2.排除等效冗余
在搜索过程中,如果我们能判定从搜索树当前节点沿着几条不同的分支到达的子树是等效的,那么只需要对一条分支执行搜索。
3.可行性剪枝
在搜索过程中,及时对当前状态进行检查,如果发现分支已经无法到达递归边界就执行回溯。
某些问题的条件范围是一个区间,此时可行性剪枝也被称为“上下界剪枝”。
4.最优性剪枝
在最优化问题的搜索过程中,如果当前花费的代价已经超过了当前搜到的最优解,无论采取多么优秀的策略到达边界,都不可能更新答案。此时可以停止对该分支的搜索,执行回溯。
5.记忆化
可以记录每个状态的搜索结果,在重复遍历一个状态时直接检索并返回。这就好比我们对图进行深度优先遍历时,标记一个节点是否被访问过。
在小猫爬山和数独问题中,搜索算法的状态空间其实都是“树”形,不会重复访问,所以不需要进行记录。
例题
acwing167.木棒
搜索的状态包括已经拼好的木棍根数,正在拼的当前木棍的长度,每根木棍的使用情况。 在各个状态下,我们从尚未使用的木棍里选择一个,尝试频道当前的原始木棒里。
剪枝策略
1.从小到大枚举原始木棒的长度len,当然应为sum的约数(可行性),木棍的根数cnt=sum/len。
2.把木棍从小到大排序,优先尝试较长的木棍。(优化搜索顺序)
3.排除等效冗余
(1).限制先后加入一根原始木棒的长度是递减的。例如312,123,231本质上是等效的。
(2).对于原始木棒,记录最近一次尝试拼接的长度,如果失败不在尝试拼接其他相同长度的小木棍。
(3).如果当前原始木棒中“尝试拼接第一根木棍”的递归分支就返回失败,那么直接判定当前分支失败,立即回溯。
证明:后面还没有进行拼接的原始木棒和当前这一个木棒是等效的,如果当前失败,那么拼到后面也会失败。
(4).如果在当前原始木棒中拼入一根木棍后,木棒恰到拼接完整,并且接下来拼接剩余原始木棒的递归分支返回失败,那么直接判定当前分支失败,立即回溯。
证明:如果不拼接这一根木棍,那么就是拼接若干根更小的,根据贪心的思想肯定不会比现在更优。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int a[100],v[100];
int n,sum,len,cnt;
//正在拼第stick根木棒
//第stick根木棒当前长度是s
//拼接到第stick根木棒中的上一根小木棍是last
bool dfs(int stick,int s,int last)
{if(stick>cnt)return true;//搜索成功if(s==len)return dfs(stick+1,0,1);//去拼下一根for(int i=last;i<=n;i++)//剪枝3-1{if(v[i]||s+a[i]>len)continue;v[i]=1;if(dfs(stick,s+a[i],last+1))return true;v[i]=0;int j=i+1;//剪枝3-2while(j<n&&a[i]==a[j])j++;i=j-1;if(!s||s+a[i]==len)return false;//剪枝3-3,3-4}return false;//所有分支均尝试过,搜索失败
}
int main()
{while(cin>>n,n){sum=0;memset(v,0,sizeof v);for(int i=1;i<=n;i++){cin>>a[i];sum+=a[i];}sort(a+1,a+1+n);reverse(a+1,a+1+n);for(len=a[1];len<=sum;len++){if(sum%len)continue;cnt=sum/len;if(dfs(1,0,1)){cout<<len<<endl;break;}}}return 0;
}
acwing168.生日蛋糕
1.优化搜索顺序
层间为从下往上搜索,层间先枚举r再枚举h,均为从大向小枚举。
2.上下界剪枝
u ≤ R u ≤ m i n { R u + 1 − 1 , n − v u } u \leq R_{u} \leq min\{R_{u+1}-1,\sqrt{\frac{n-v}{u}}\} u≤Ru≤min{Ru+1−1,un−v}
u ≤ H u ≤ m i n { H u + 1 − 1 , n − v R u 2 } u \leq H_{u} \leq min\{H_{u+1}-1,\frac{n-v}{R_u^2}\} u≤Hu≤min{Hu+1−1,Ru2n−v}
3.可行性剪枝
预处理从上往下的最小体积minv和侧面积mins。如果当前体积v加上上面所有层的最小体积大于n,可以剪枝。
4.最优性剪枝1
如果当前表面积s加上上面所有层的最小表面积大于等于ans,可以剪枝。
5.最优性剪枝2
上面所有层的体积可以表示为
n − v = ∑ k = 1 d e p − 1 H [ k ] ∗ R [ k ] 2 n-v=\sum_{k=1}^{dep-1}H[k]*R[k]^2 n−v=∑k=1dep−1H[k]∗R[k]2
上面所有层的表面积可以表示为
2 ∑ k = 1 d e p − 1 H [ k ] ∗ R [ k ] = 2 R [ d e p ] ∑ k = 1 d e p − 1 H [ k ] ∗ R [ k ] ∗ R [ d e p ] ≥ 2 R [ d e p ] ∑ k = 1 d e p − 1 H [ k ] ∗ R [ k ] 2 ≥ 2 ( n − v ) R [ d e p ] 2\sum_{k=1}^{dep-1}H[k]*R[k]=\frac{2}{R[dep]}\sum_{k=1}^{dep-1}H[k]*R[k]*R[dep] \geq \frac{2}{R[dep]}\sum_{k=1}^{dep-1}H[k]*R[k]^2 \geq \frac{2(n-v)}{R[dep]} 2∑k=1dep−1H[k]∗R[k]=R[dep]2∑k=1dep−1H[k]∗R[k]∗R[dep]≥R[dep]2∑k=1dep−1H[k]∗R[k]2≥R[dep]2(n−v)
所以当 2 ( n − v ) R [ d e p ] + s \frac{2(n-v)}{R[dep]}+s R[dep]2(n−v)+s大于已经搜索到的答案时,可以剪枝。
#include<iostream>
#include<cmath>
using namespace std;
#define INF 1e9
int n,m;
int minv[25],mins[25];
int r[25],h[25];
int ans=INF;
void dfs(int u,int v,int s)
{if(!u){if(v==n)ans=min(ans,s);return ;}if(v+minv[u]>n)return ;if(s+mins[u]>=ans)return ;if(s+2*(n-v)/r[u+1]>=ans)return ;for(int i=min(r[u+1]-1,(int)sqrt((n-v)/u));i>=u;i--){for(int j=min(h[u+1]-1,(n-v)/i/i);j>=u;j--){int t=0;if(u==m)t=i*i;r[u]=i;h[u]=j;dfs(u-1,v+i*i*j,s+t+2*i*j);}}
}
int main()
{cin>>n>>m;for(int i=1;i<=m;i++){minv[i]=minv[i-1]+i*i*i;mins[i]=mins[i-1]+2*i*i;}r[m+1]=h[m+1]=INF;dfs(m,0,0);if(ans!=INF)cout<<ans;else cout<<0;return 0;
}
acwing169数独2
总体思路:每次找到一个空格,枚举空格选择哪个字母,然后往下递归。
边界:所有空格都填完。
然后有很多剪枝:
1、对于每个空格,如果不能填任何一个字母,则无解;如果只能填一个字母,那么直接填上;
2、对于每一行,如果某个字母不能出现在任何一个位置,则无解;如果某个字母只有一个位置可以填,则直接填上;
3、对于每一列,同2;
4、对于每个16宫格,同2;
5、每次选择空格时,选择备选方案(能填的字母数量)最少的格子来填。
#include <bits/stdc++.h>
using namespace std;
const int N=16;
int ones[1<<N],cnt_log[1<<N];//ones[x]表示x在二进制下有多少个1;log[x]表示log(x)的值
int state[N][N];//状态存储,表示x行y列这个格子可以填哪些数(0-15),15位二进制表示
char str[N][N+1];
int bstate[N*N+1][N][N],bstate2[N*N+1][N][N];//bstate和bstate2都存储状态的备份(搜索最多有N*N层,每层有一个备份)
char bstr[N*N+1][N][N+1];//输入的N宫格也要备份 inline int lowbit(int x)//返回x在二进制下的最后一个1 (inline加速函数调用过程)
{return x & -x;
}void draw(int x,int y,int c)//在(x,y)这个格子上写上字母c(0到15表示A到P)
{str[x][y]='A'+c;//先写进去,转换为原来的字母 for (int i=0;i<N;++i)//更新state {state[x][i] &= ~(1 << c);//x这一行其他位置都不能再填c (把表示c的二进制位改成0,yxc大佬的位运算)state[i][y] &= ~(1 << c);//y这一列其他位置都不能再填c }int sx=x/4*4,sy=y/4*4;//把(x,y)所在的十六宫格也做一次同样的操作 for (int i=0;i<4;++i)for (int j=0;j<4;++j)state[sx+i][sy+j] &= ~(1 << c);//同上 state[x][y]=1<<c;
}bool dfs(int cnt)//传入的参数cnt表示当前空格个数
{if (!cnt) return true;//cnt为零就找到了方案,返回trueint kcnt=cnt;//先进行备份 //剪枝1:对于每个空格,如果不能填任何一个字母,则返回false;如果只能填一个字母,那么直接填上for (int i=0;i<N;++i)//直接枚举所有的空格for (int j=0;j<N;++j)if (str[i][j]=='-')//如果当前格子是空格 {if (!state[i][j])//如果不能填任何一个字母,则返回false;并且copy回去 {return false;}if (ones[state[i][j]]==1)//如果只能填一个字母,那么直接填上{draw(i,j,cnt_log[state[i][j]]);--cnt;//填好一个空格,所以剩余空格数减1}}//剪枝2:对于每一行,如果某个字母不能出现在任何一个位置,则返回false;如果某个字母只有一个位置可以填,则直接填上 for (int i=0;i<N;++i)//枚举所有行 {int sor=0,sand=(1<<N)-1;//sor存的是这一行里每个格子备选方案的并集;sand用来找“如果某个字母只有一个位置可以填”,先假设所有字母都符合要求 int drawn=0;//drawn表示所有已经填上的字母是哪些 for (int j=0;j<N;++j)//枚举当前行所有格子 {int s=state[i][j];//只是为了少打字 sand &= ~(sor & s);//把不符合要求的删掉(和前面更新state是一个道理) sor |= s;//求并集 if (str[i][j]!='-') drawn |= state[i][j];//如果当前这个位置已经填上字母,就记录下来 }if (sor!=(1<<N)-1)//如果这个并集不够A到P就是无解 {return false;}//这样以后sand中是1的位置就表示这个字母有一个位置可以填for (int j=sand;j;j-=lowbit(j))//所以把所有是1的位置枚举一遍 {int t=lowbit(j);//也是为了少写一点 if (!(drawn & t))//如果正好也没填过就填上 {for (int k=0;k<N;++k)//更新state if (state[i][k] & t){draw(i,k,cnt_log[t]);--cnt;break;}}}}//剪枝3:对于每一列,同剪枝2 (直接把上面复制过来再把i和j调换一下就好了) for (int i=0;i<N;++i){int sor=0,sand=(1<<N)-1;int drawn=0;for (int j=0;j<N;++j){int s=state[j][i];sand &= ~(sor & s);sor |= s;if (str[j][i]!='-') drawn |= state[j][i];}if (sor!=(1<<N)-1){return false;}for (int j=sand;j;j-=lowbit(j)){int t=lowbit(j);if (!(drawn & t)){for (int k=0;k<N;++k)if (state[k][i] & t)//这里i和k也要和上面要反一下 {draw(k,i,cnt_log[t]);--cnt;break;}}}}//剪枝4:对于每个N宫格,同剪枝2for (int i=0;i<N;++i)//i枚举每个N宫格的位置 {int sor=0,sand=(1<<N)-1;int drawn=0;for (int j=0;j<N;++j)//j枚举一个N宫格的每个位置 {int sx=i/4*4,sy=i%4*4;int dx=j/4,dy=j%4;//需要定义一个偏移量 int s=state[sx+dx][sy+dy];sand &= ~(sor & s);sor |= s;if (str[sx+dx][sy+dy]!='-') drawn |= state[sx+dx][sy+dy];}if (sor!=(1<<N)-1){return false;}for (int j=sand;j;j-=lowbit(j)){int t=lowbit(j);if (!(drawn & t)){for (int k=0;k<N;++k){int sx=i/4*4,sy=i%4*4;int dx=k/4,dy=k%4;if (state[sx+dx][sy+dy] & t){draw(sx+dx,sy+dy,cnt_log[t]);--cnt;break;}}}}}//啊,还剩一个剪枝啦 //剪枝5:每次选择空格时,选择备选方案(能填的字母数量)最少的格子来填 if (!cnt) return true;//哦对,先看看现在有没有填完(一个小剪枝) int x,y,s=100;//(x,y)存储最后选择的格子,s是备选方案最小值 for (int i=0;i<N;++i)//遍历一遍所有的格子 for (int j=0;j<N;++j)if (str[i][j]=='-' && ones[state[i][j]]<s)//如果当前格子还没填过,并且这个格子的备选方案更少,就更新 {s=ones[state[i][j]];x=i,y=j;}//求完了那个格子备选方案最少,然后枚举应该在这个格子填那个字母 memcpy(bstate[kcnt],state,sizeof state);//先备份一下,bstate2在这里终于用到了 memcpy(bstr[kcnt],str,sizeof str);for (int i=state[x][y];i;i-=lowbit(i))//枚举这个格子的备选方案 {draw(x,y,cnt_log[lowbit(i)]);if (dfs(cnt-1)) return true;//进行下一层递归,如果成功,返回true memcpy(state,bstate[kcnt],sizeof state);memcpy(str,bstr[kcnt],sizeof str);}//失败了也要copy回来 memcpy(state,bstate[kcnt],sizeof state);memcpy(str,bstr[kcnt],sizeof str);return false;//一直没找到返回false
}int main()
{for (int i=0;i<N;++i) cnt_log[1<<i]=i;//预处理cnt_log数组,如log(2)=1,log(4)=2,log(8)=3 for (int i=0;i<(1<<N);++i)//预处理ones数组 for (int j=i;j;j-=lowbit(j))//j每次减去最后一个1 ++ones[i];//每减一个1说明这个i就多一个1 while (cin>>str[0])//多组测试数据 {for (int i=1;i<N;++i) cin>>str[i];for (int i=0;i<N;++i)//预处理statefor (int j=0;j<N;++j)state[i][j]=(1<<N)-1;//一开始假设所有空格都是空的int cnt=0;//存储空格个数for (int i=0;i<N;++i)//接着在遍历一遍,看那些格子已经填好了for (int j=0;j<N;++j)if (str[i][j]!='-') draw(i,j,str[i][j]-'A');//如果已经填好了就更新state,A到P分别用0到15表示else ++cnt;dfs(cnt);//DFS开始for (int i=0;i<N;++i) cout<<str[i]<<endl;//输出答案puts("");//每次输出完答案加一个空行}return 0;
}
相关文章:

《算法竞赛进阶指南》0x23剪枝
剪枝,就是减少搜索树的规模、尽可能排除搜索书中不必要的分支的一种手段。形象地看,就好像剪掉了搜索树的枝条,故被称为“剪枝”。在深度优先搜索中,有以下常见的剪枝方法。 1.优化搜索顺序 在一些搜索问题中,搜索树的…...

同态加密和SEAL库的介绍(三)BFV - Batch Encoder
写在前面: 在上一篇中展示了如何使用 BFV 方案执行一个非常简单的计算。该计算在 plain_modulus 参数下进行,并且仅使用了 BFV 明文多项式中的一个系数。这种方法有两个显著的问题: 实际应用通常使用整数或实数运算,而不是模运算…...
Docker 环境下使用 Traefik v3 和 MinIO 快速搭建私有化对象存储服务
上一篇文章中,我们使用 Traefik 新版本完成了本地服务网关的搭建。接下来,来使用 Traefik 的能力,进行一系列相关的基础设施搭建吧。 本篇文章,聊聊 MinIO 的单独使用,以及结合 Traefik 完成私有化 S3 服务的基础搭建…...

玛雅房产系统源码开发与技术功能解析
引言 随着房地产市场的蓬勃发展,房产管理系统(Real Estate Management System, REMS)作为提升行业效率、优化资源配置的关键工具,其重要性日益凸显。房产系统源码开发不仅涉及复杂的业务逻辑处理,还融合了先进的软件开…...

c++----初识模板
大家好,这篇博客想与大家分享一些我们c中比较好用的知识点。模板。首先咧,我们都知道模板嘛,就是以前人的经验总结出来的知识。方便我们使用。这里的模板也是一样的。当我们学习过后,对于一些在c中的自定义函数,我们在…...

SpringBoot3热部署
引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId><scope>runtime</scope><optional>true</optional> </dependency> 默认就是,无需配置 可以了…...

J. 二进制与、平方和
https://codeforces.com/gym/104095/problem/J 分析操作一 1&00 ,0&10,ai<qmi(2,24),说明每个数最多操作25次 维护区间或和,orsum & x orsum 就不用递归下去了 势能线段树code // Problem: J. 二进制与、平方和 // Contest: Codeforc…...

LVS中NAT模式和DR模式实战讲解
1DR模式 DR:Direct Routing,直接路由,LVS默认模式,应用最广泛,通过为请求报文重新封装一个MAC首部进行 转发,源MAC是DIP所在的接口的MAC,目标MAC是某挑选出的RS的RIP所在接口的MAC地址;源 IP/PORT…...

写给小白程序员的一封信
文章目录 1.编程小白如何成为大神?大学新生的最佳入门攻略2.程序员的练级攻略3.编程语言的选择4.熟悉Linux5.学会git6.知道在哪寻求帮助7.多结交朋友8.参加开源项目9.坚持下去 1.编程小白如何成为大神?大学新生的最佳入门攻略 编程已成为当代大学生的必…...

Leaf分布式ID
文章目录 系统对Id号的要求UUIDsnowflakeLeafLeaf-snowflakeLeaf-segmentMySQL自增主键segment双buffer 系统对Id号的要求 1、业务 1)全局唯一性:不能出现重复的ID号,既然是唯一标识,这是最基本的要求 2)趋势递增&a…...

Starrocks解析json数组
json数据 [{"spec": "70g/支","unit": "支","skuId": "1707823848651276346","amount": 6,"weight": 70,"spuName": "伊利 甄稀 苦咖啡味雪糕 流心冰淇淋 70g/支",&quo…...
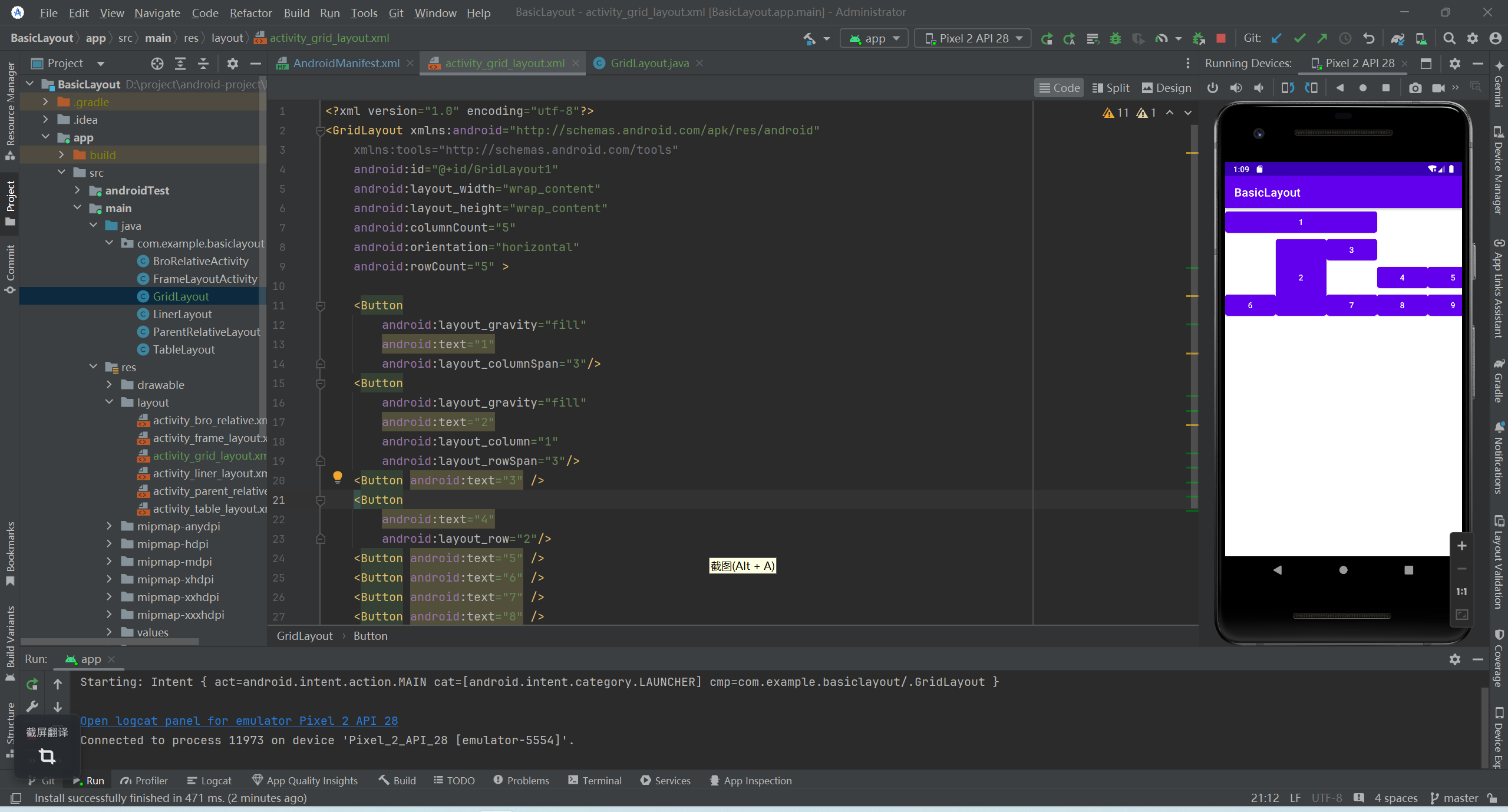
安卓基本布局(下)
TableLayout 常用属性描述collapseColumns设置需要被隐藏的列的列号。shrinkColumns设置允许被伸缩的列的列号。stretchColumns设置允许被拉伸的列的列号。 <TableLayout xmlns:android"http://schemas.android.com/apk/res/android"android:id"id/TableL…...

Python中使用正则表达式
摘要: 正则表达式,又称为规则表达式,它不是某种编程语言所特有的,而是计算机科学的一个概念,通常被用来检索和替换某些规则的文本。 一.正则表达式的语法 ①行定位符 行定位符就是用来描述字符串的边界。"^&qu…...

三大口诀不一样的代码,小小的制表符和换行符玩的溜呀
# 小案例,打印输出加法口诀 for i in range(1,10):for j in range(1,10):if j>i:breakprint(f"{j}{i}{ji}".strip(),end\t)print() print(\n) for i in range(1,10):for j in range(1,10):if j>i:breakprint(f"{j}x{i}{j*i}",end\t)print…...

[qt] 线程等待与唤醒
对于生产者与消费者的数据处理的另一种好的解决方法是使用QWaitCondition类,允许线程在一定的条件下唤醒其他多个线程来共同处理。 一 定义公共变量 DataSize: 生产者生产数据的大小BufferSize: 也就是这个缓冲区的大小,每个单元是一个int,也有可能是一个链表,结构…...

Springboot 实现 Modbus Rtu 协议接入物联网设备
Modbus RTU 技术教程 引言 Modbus是一种开放标准的通信协议,它最初由Modicon(现施耐德电气)在1979年发布,旨在让可编程逻辑控制器(PLC)之间能够进行通信。随着时间的发展,Modbus已经成为工业自动化领域中最常用的通信协议之一,尤其适用于连接工业电子设备。本文将详细…...

鸿蒙笔记--装饰器
这一节主要了解一下鸿蒙里的装饰器,装饰器是一种特殊的语法结构,用于装饰类、结构体、方法以及变量; 1 Component在鸿蒙(HarmonyOS)开发中扮演着重要角色,主要用于定义可重用的UI组件,主要作用:1)组件化:Component装饰…...
不同环境下RabbitMQ的安装-3 操作RabbitMQ
前面两篇从不同环境下RabbitMQ的安装-1 为什么要使用消息服务 到同环境下RabbitMQ的安装-2 ARM架构、X86架构、Window系统环境下安装RabbitMQ介绍了关于如何在ARM架构、X86架构和Window系统下如何安装,各位小伙伴可以根据自己的实际开发场景参考安装。 到本篇是一些…...

postgregSQL配置vector插件
1.下载vector 下载vector:https://pgxn.org/dist/vector/0.5.1/ 放在:C:\Program Files\PostgreSQL\vector-0.5.1 2.安装Visual Studio 2022 下载:https://visualstudio.microsoft.com/zh-hans/downloads/ 安装Visual Studio是为了C编译环…...
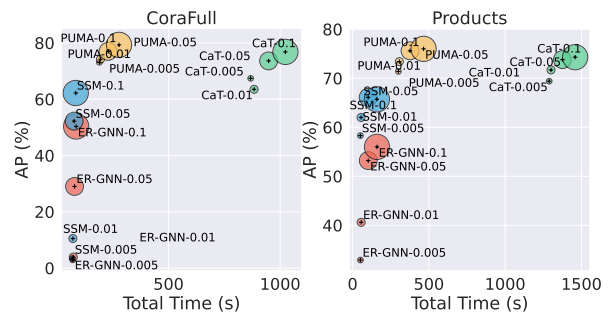
PUMA论文阅读
PUMA: Efficient Continual Graph Learning with Graph Condensation PUMA:通过图压缩进行高效的连续图学习 ABSTRACT 在处理流图时,现有的图表示学习模型会遇到灾难性的遗忘问题,当使用新传入的图进行学习时,先前学习的这些模…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
