同态加密和SEAL库的介绍(三)BFV - Batch Encoder
写在前面:
在上一篇中展示了如何使用 BFV 方案执行一个非常简单的计算。该计算在 plain_modulus 参数下进行,并且仅使用了 BFV 明文多项式中的一个系数。这种方法有两个显著的问题:
- 实际应用通常使用整数或实数运算,而不是模运算;
- 仅使用了明文多项式的一个系数。这实际上是非常浪费的,因为明文多项式很大,而且无论如何都会被整体加密。
如果直接增加 plain_modulus 参数,直到没有溢出发生,就能让计算表现得像整数运算。但是问题在于增加 plain_modulus 会增加噪声预算的消耗,并且还会减少初始噪声预算。接下来介绍其他将数据布局到明文元素(编码)的方法,这些方法可以允许更多的计算而不会发生数据类型溢出,并且可以充分利用整个明文多项式。
一、批处理介绍
[BatchEncoder] (适用于 BFV 或 BGV 方案)
令 N 表示 poly_modulus_degree,T 表示 plain_modulus。批处理允许将 BFV 明文多项式视为 矩阵,每个元素是模 T 的整数。在矩阵视图中,加密操作对加密矩阵进行逐元素操作,使用户能够在完全可向量化的计算中获得数个数量级的速度提升。
因此,除了最简单的计算,批处理应是与 BFV 一起使用的首选方法,并且如果使用得当,其实现将比不使用批处理的任何实现都要出色。
此外,批处理对于 BGV 方案的工作方式与此示例中的 BFV 方案类似。例如,只需将`scheme_type::bfv` 更改为 `scheme_type::bgv` 即可使此示例适用于 BGV 方案。
1.1 参数设置
EncryptionParameters parms(scheme_type::bfv);
size_t poly_modulus_degree = 8192;
parms.set_poly_modulus_degree(poly_modulus_degree);
parms.set_coeff_modulus(CoeffModulus::BFVDefault(poly_modulus_degree)); 要启用批处理,我们需要将 plain_modulus 设置为一个与 2*poly_modulus_degree 同余于 1 的素数。这个需要特别注意,因为这与普通的Encode不同,并且设置不正确的话 BatchEncoder会校验,设置为满足 的素数即可。
同时,Microsoft SEAL 提供了一个辅助方法来找到这样的素数。在这个示例中,我们创建了一个支持批处理的 20 位素数。
parms.set_plain_modulus(PlainModulus::Batching(poly_modulus_degree, 20));然后就可以用参数创建环境,并且可以通过查看 SEALContext 创建的加密参数限定符来验证批处理是否确实启用了。
SEALContext context(parms);
print_parameters(context);
auto qualifiers = context.first_context_data()->qualifiers();
cout << "批处理已启用:" << boolalpha << qualifiers.using_batching << endl; 这里输出为:
1.2 创建其他实例
这里与上篇相同,创建加解密需要的实例:
KeyGenerator keygen(context);
SecretKey secret_key = keygen.secret_key();
PublicKey public_key;
keygen.create_public_key(public_key);
RelinKeys relin_keys;
keygen.create_relin_keys(relin_keys);
Encryptor encryptor(context, public_key);
Evaluator evaluator(context);
Decryptor decryptor(context, secret_key);但是注意,编码器与之前不同,批处理通过 BatchEncoder 类的实例进行。:
BatchEncoder batch_encoder(context);二、批处理运算
这里需要格外注意槽的概念,批处理 `槽` 的总数等于 poly_modulus_degree,N,这些槽被组织成 矩阵,可以对其进行加密和计算。每个槽包含一个模 plain_modulus 的整数。
即这里每一个明文或者密文块,可以用的槽数量就是 N,但是内部不是一整个连续存储。逻辑上可以认为是两行的一个矩阵,但是物理上其实是类似于单链表的一种存储形式。
这里可以查看可用的槽数量,当然为了清晰一行有多少个,可以定义一个 row_size:
size_t slot_count = batch_encoder.slot_count();
size_t row_size = slot_count / 2;为了帮助大家理解存储的逻辑形式,这里放几个数字并打印:
vector<uint64_t> pod_matrix(slot_count, 0ULL);
pod_matrix[0] = 0ULL;
pod_matrix[1] = 1ULL;
pod_matrix[2] = 2ULL;
pod_matrix[3] = 3ULL;
pod_matrix[row_size] = 4ULL;
pod_matrix[row_size + 1] = 5ULL;
pod_matrix[row_size + 2] = 6ULL;
pod_matrix[row_size + 3] = 7ULL;
2.1 输入的编码与加密
使用 BatchEncoder 将矩阵编码成一个明文多项式,并加密:(注意上面是根据 solt_count 创建的输入容器,编码完成后是一个 Plaintext 块,加密完是 Ciphertext 块)
Plaintext plain_matrix;
batch_encoder.encode(pod_matrix, plain_matrix);
Ciphertext encrypted_matrix;
encryptor.encrypt(plain_matrix, encrypted_matrix);
cout <<decryptor.invariant_noise_budget(encrypted_matrix) << " bits";在示例中这里加密完后立刻解密进行验证,并输出噪声预算:

对密文的操作会同时在所有 8192 个槽(矩阵元素)上同态执行。为了演示计算,这里编码一个明文矩阵:
vector<uint64_t> pod_matrix2;
for (size_t i = 0; i < slot_count; i++)
{pod_matrix2.push_back((i & size_t(0x1)) + 1);
}
Plaintext plain_matrix2;
batch_encoder.encode(pod_matrix2, plain_matrix2);
2.2 运算
这里展示的运算是:将第二个(明文)矩阵加到加密矩阵上,并对和进行平方。
evaluator.add_plain_inplace(encrypted_matrix, plain_matrix2);
evaluator.square_inplace(encrypted_matrix);
evaluator.relinearize_inplace(encrypted_matrix, relin_keys);输出噪声,并对结果进行解密解码并打印:
cout <<decryptor.invariant_noise_budget(encrypted_matrix) << " bits";
decryptor.decrypt(encrypted_matrix, plain_result);
batch_encoder.decode(plain_result, pod_result);
从结果可以看出来,两个向量用 Batch Encoder 编码后进行的运算,是对应位置进行的加法和点乘!
三、总结
当所需的加密计算高度并行化时,批处理允许我们高效地使用整个明文多项式。但是,它尚未解决在文件开头提到的另一个问题:每个槽只包含一个模 plain_modulus 的整数,除非plain_modulus 非常大,否则我们可能会很快遇到数据类型溢出并在需要进行整数计算时得到意外的结果。请注意,溢出无法在加密形式中检测到。
CKKS 方案(及其编码器 CKKSEncoder)解决了数据类型溢出问题,但代价是只能得到近似结果(下篇预告)。
相关文章:

同态加密和SEAL库的介绍(三)BFV - Batch Encoder
写在前面: 在上一篇中展示了如何使用 BFV 方案执行一个非常简单的计算。该计算在 plain_modulus 参数下进行,并且仅使用了 BFV 明文多项式中的一个系数。这种方法有两个显著的问题: 实际应用通常使用整数或实数运算,而不是模运算…...
Docker 环境下使用 Traefik v3 和 MinIO 快速搭建私有化对象存储服务
上一篇文章中,我们使用 Traefik 新版本完成了本地服务网关的搭建。接下来,来使用 Traefik 的能力,进行一系列相关的基础设施搭建吧。 本篇文章,聊聊 MinIO 的单独使用,以及结合 Traefik 完成私有化 S3 服务的基础搭建…...

玛雅房产系统源码开发与技术功能解析
引言 随着房地产市场的蓬勃发展,房产管理系统(Real Estate Management System, REMS)作为提升行业效率、优化资源配置的关键工具,其重要性日益凸显。房产系统源码开发不仅涉及复杂的业务逻辑处理,还融合了先进的软件开…...

c++----初识模板
大家好,这篇博客想与大家分享一些我们c中比较好用的知识点。模板。首先咧,我们都知道模板嘛,就是以前人的经验总结出来的知识。方便我们使用。这里的模板也是一样的。当我们学习过后,对于一些在c中的自定义函数,我们在…...

SpringBoot3热部署
引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId><scope>runtime</scope><optional>true</optional> </dependency> 默认就是,无需配置 可以了…...

J. 二进制与、平方和
https://codeforces.com/gym/104095/problem/J 分析操作一 1&00 ,0&10,ai<qmi(2,24),说明每个数最多操作25次 维护区间或和,orsum & x orsum 就不用递归下去了 势能线段树code // Problem: J. 二进制与、平方和 // Contest: Codeforc…...

LVS中NAT模式和DR模式实战讲解
1DR模式 DR:Direct Routing,直接路由,LVS默认模式,应用最广泛,通过为请求报文重新封装一个MAC首部进行 转发,源MAC是DIP所在的接口的MAC,目标MAC是某挑选出的RS的RIP所在接口的MAC地址;源 IP/PORT…...

写给小白程序员的一封信
文章目录 1.编程小白如何成为大神?大学新生的最佳入门攻略2.程序员的练级攻略3.编程语言的选择4.熟悉Linux5.学会git6.知道在哪寻求帮助7.多结交朋友8.参加开源项目9.坚持下去 1.编程小白如何成为大神?大学新生的最佳入门攻略 编程已成为当代大学生的必…...

Leaf分布式ID
文章目录 系统对Id号的要求UUIDsnowflakeLeafLeaf-snowflakeLeaf-segmentMySQL自增主键segment双buffer 系统对Id号的要求 1、业务 1)全局唯一性:不能出现重复的ID号,既然是唯一标识,这是最基本的要求 2)趋势递增&a…...

Starrocks解析json数组
json数据 [{"spec": "70g/支","unit": "支","skuId": "1707823848651276346","amount": 6,"weight": 70,"spuName": "伊利 甄稀 苦咖啡味雪糕 流心冰淇淋 70g/支",&quo…...
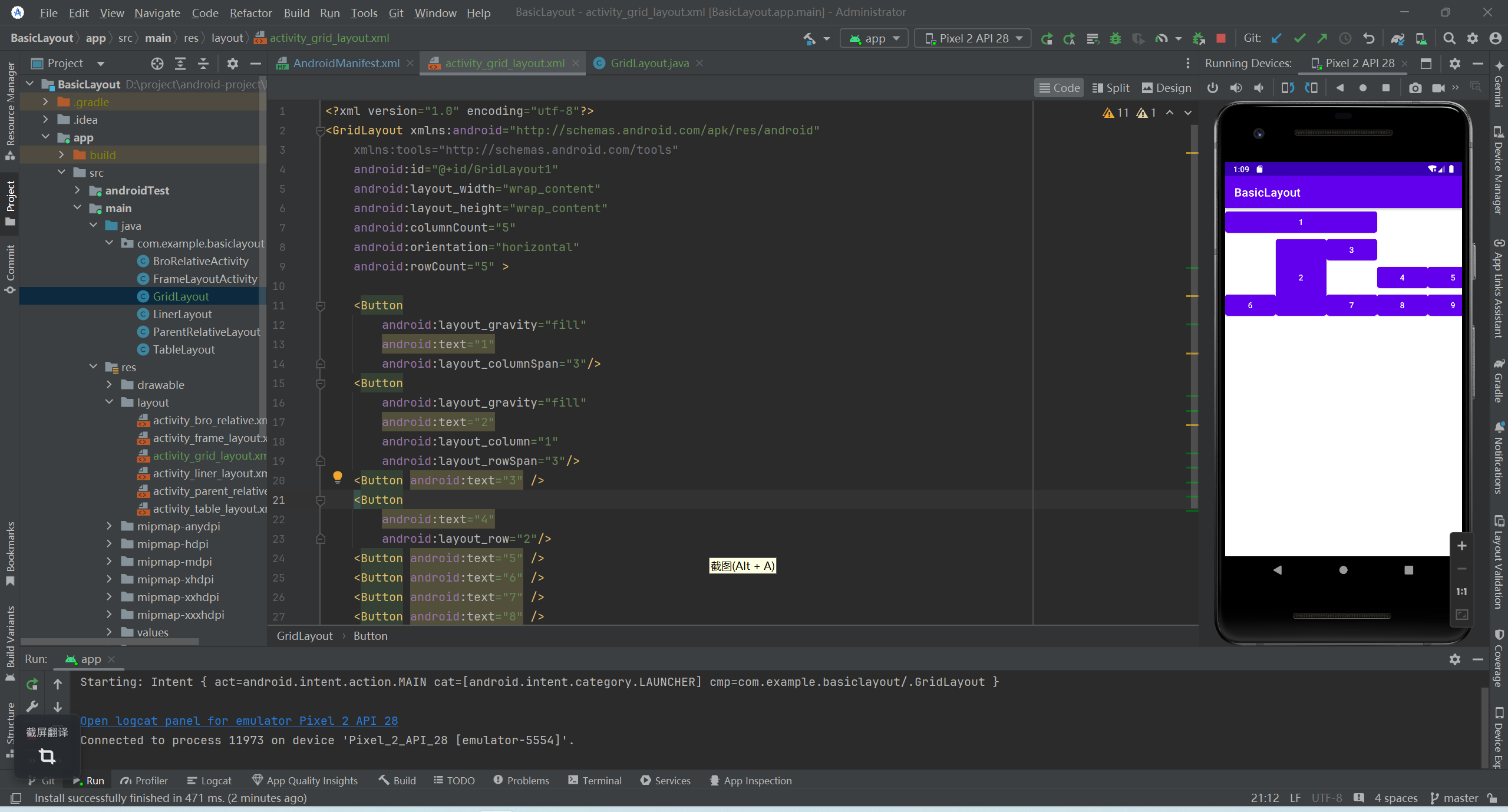
安卓基本布局(下)
TableLayout 常用属性描述collapseColumns设置需要被隐藏的列的列号。shrinkColumns设置允许被伸缩的列的列号。stretchColumns设置允许被拉伸的列的列号。 <TableLayout xmlns:android"http://schemas.android.com/apk/res/android"android:id"id/TableL…...

Python中使用正则表达式
摘要: 正则表达式,又称为规则表达式,它不是某种编程语言所特有的,而是计算机科学的一个概念,通常被用来检索和替换某些规则的文本。 一.正则表达式的语法 ①行定位符 行定位符就是用来描述字符串的边界。"^&qu…...

三大口诀不一样的代码,小小的制表符和换行符玩的溜呀
# 小案例,打印输出加法口诀 for i in range(1,10):for j in range(1,10):if j>i:breakprint(f"{j}{i}{ji}".strip(),end\t)print() print(\n) for i in range(1,10):for j in range(1,10):if j>i:breakprint(f"{j}x{i}{j*i}",end\t)print…...

[qt] 线程等待与唤醒
对于生产者与消费者的数据处理的另一种好的解决方法是使用QWaitCondition类,允许线程在一定的条件下唤醒其他多个线程来共同处理。 一 定义公共变量 DataSize: 生产者生产数据的大小BufferSize: 也就是这个缓冲区的大小,每个单元是一个int,也有可能是一个链表,结构…...

Springboot 实现 Modbus Rtu 协议接入物联网设备
Modbus RTU 技术教程 引言 Modbus是一种开放标准的通信协议,它最初由Modicon(现施耐德电气)在1979年发布,旨在让可编程逻辑控制器(PLC)之间能够进行通信。随着时间的发展,Modbus已经成为工业自动化领域中最常用的通信协议之一,尤其适用于连接工业电子设备。本文将详细…...

鸿蒙笔记--装饰器
这一节主要了解一下鸿蒙里的装饰器,装饰器是一种特殊的语法结构,用于装饰类、结构体、方法以及变量; 1 Component在鸿蒙(HarmonyOS)开发中扮演着重要角色,主要用于定义可重用的UI组件,主要作用:1)组件化:Component装饰…...
不同环境下RabbitMQ的安装-3 操作RabbitMQ
前面两篇从不同环境下RabbitMQ的安装-1 为什么要使用消息服务 到同环境下RabbitMQ的安装-2 ARM架构、X86架构、Window系统环境下安装RabbitMQ介绍了关于如何在ARM架构、X86架构和Window系统下如何安装,各位小伙伴可以根据自己的实际开发场景参考安装。 到本篇是一些…...

postgregSQL配置vector插件
1.下载vector 下载vector:https://pgxn.org/dist/vector/0.5.1/ 放在:C:\Program Files\PostgreSQL\vector-0.5.1 2.安装Visual Studio 2022 下载:https://visualstudio.microsoft.com/zh-hans/downloads/ 安装Visual Studio是为了C编译环…...
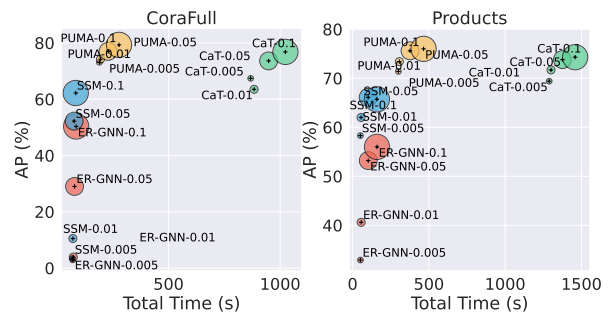
PUMA论文阅读
PUMA: Efficient Continual Graph Learning with Graph Condensation PUMA:通过图压缩进行高效的连续图学习 ABSTRACT 在处理流图时,现有的图表示学习模型会遇到灾难性的遗忘问题,当使用新传入的图进行学习时,先前学习的这些模…...
)
算法学习day31(动态规划)
一、比特位计数 给你一个整数 n ,对于 0 < i < n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n 1 的数组 ans 作为答案。 输入:n 2 输出:[0,1,1] 解释:0 --> 0 1 --> 1 2 -…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

短视频时长预估算法调研
weighted LR o d d s T p 1 − p ( 1 − p ) o d d s T p ( T p o d d s ∗ p ) o d d s p o d d s T o d d s odds \frac{Tp}{1-p} \newline (1-p)odds Tp \newline (Tp odds * p) odds \newline p \frac{odds}{T odds} \newline odds1−pTp(1−p)oddsTp(Tpodds…...
