J. 二进制与、平方和
https://codeforces.com/gym/104095/problem/J

分析操作一
1&0=0 ,0&1=0,ai<=qmi(2,24),说明每个数最多操作25次
维护区间或和,orsum & x== orsum 就不用递归下去了
势能线段树code
// Problem: J. 二进制与、平方和
// Contest: Codeforces - 2020 CCPC Henan Provincial Collegiate Programming Contest
// URL: https://codeforces.com/gym/104095/problem/J
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long long LL;
const int N=3e5+9;
const int mod=998244353;
int a[N];
template<class T>
constexpr T power(T a, LL b) {T res = 1;for (; b; b /= 2, a *= a) {if (b % 2) {res *= a;}}return res;
}template<int P>
struct MInt {int x;constexpr MInt() : x{} {}constexpr MInt(LL x) : x{norm(x % getMod())} {}static int Mod;constexpr static int getMod() {if (P > 0) {return P;} else {return Mod;}}constexpr static void setMod(int Mod_) {Mod = Mod_;}constexpr int norm(int x) const {if (x < 0) {x += getMod();}if (x >= getMod()) {x -= getMod();}return x;}constexpr int val() const {return x;}explicit constexpr operator int() const {return x;}constexpr MInt operator-() const {MInt res;res.x = norm(getMod() - x);return res;}constexpr MInt inv() const {assert(x != 0);return power(*this, getMod() - 2);}constexpr MInt &operator*=(MInt rhs) & {x = 1LL * x * rhs.x % getMod();return *this;}constexpr MInt &operator+=(MInt rhs) & {x = norm(x + rhs.x);return *this;}constexpr MInt &operator-=(MInt rhs) & {x = norm(x - rhs.x);return *this;}constexpr MInt &operator/=(MInt rhs) & {return *this *= rhs.inv();}friend constexpr MInt operator*(MInt lhs, MInt rhs) {MInt res = lhs;res *= rhs;return res;}friend constexpr MInt operator+(MInt lhs, MInt rhs) {MInt res = lhs;res += rhs;return res;}friend constexpr MInt operator-(MInt lhs, MInt rhs) {MInt res = lhs;res -= rhs;return res;}friend constexpr MInt operator/(MInt lhs, MInt rhs) {MInt res = lhs;res /= rhs;return res;}friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {LL v;is >> v;a = MInt(v);return is;}friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {return os << a.val();}friend constexpr bool operator==(MInt lhs, MInt rhs) {return lhs.val() == rhs.val();}friend constexpr bool operator!=(MInt lhs, MInt rhs) {return lhs.val() != rhs.val();}
};template<>
int MInt<0>::Mod =998244353;template<int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();constexpr int P =998244353;
using Z = MInt<P>;const int mxn = 2e5 + 10;
struct SNSEG{#define ll long long #define tl(id) (id<<1)#define tr(id) (id<<1|1)#define li inlinestruct node{Z pfval;int orsum;}seg[N<<2];#define pushup(id) seg[id].pfval=seg[tl(id)].pfval+seg[tr(id)].pfval, seg[id].orsum=seg[tl(id)].orsum|seg[tr(id)].orsum;li int inrange(int L,int R,int l,int r){return L>=l && R<=r;}li int outofrange(int L,int R,int l,int r){return L>r || l>R;}li void build(int id,int l,int r){if(l==r){seg[id].pfval=1ll*a[l]*a[l];// seg[id].val=a[l];seg[id].orsum=a[l];return;}int mid=(l+r)>>1;build(tl(id),l,mid);build(tr(id),mid+1,r);pushup(id);}li Z query(int id,int L,int R,int l,int r){if(inrange(L,R,l,r)){return seg[id].pfval;}else if(!outofrange(L,R,l,r)){int mid=(L+R)>>1;return query(tl(id),L,mid,l,r)+query(tr(id),mid+1,R,l,r);}else{return 0;}}li void modify(int id,int L,int R,int l,int r,int x){if(L==R){// seg[id].val&=x;seg[id].orsum&=x;//修改seg[id].pfval=1ll*seg[id].orsum*seg[id].orsum;return;}int mid=(L+R)>>1;if(mid>=l && (seg[tl(id)].orsum&x)!=(seg[tl(id)].orsum)){modify(tl(id),L,mid,l,r,x);}if(mid<r && (seg[tr(id)].orsum&x)!=(seg[tr(id)].orsum)){modify(tr(id),mid+1,R,l,r,x);}pushup(id);}
}t;
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}t.build(1,1,n);int q;cin>>q;for(int i=1;i<=q;i++){int op;cin>>op;if(op==1){int l,r,x;cin>>l>>r>>x;t.modify(1,1,n,l,r,x);}else{int l,r;cin>>l>>r;cout<<t.query(1,1,n,l,r)<<'\n'; }// for(int i=1;i<=n;i++){// cout<<t.ask(1,1,n,i)<<" ";// }// cout<<'\n';}return 0;
}相关文章:

J. 二进制与、平方和
https://codeforces.com/gym/104095/problem/J 分析操作一 1&00 ,0&10,ai<qmi(2,24),说明每个数最多操作25次 维护区间或和,orsum & x orsum 就不用递归下去了 势能线段树code // Problem: J. 二进制与、平方和 // Contest: Codeforc…...

LVS中NAT模式和DR模式实战讲解
1DR模式 DR:Direct Routing,直接路由,LVS默认模式,应用最广泛,通过为请求报文重新封装一个MAC首部进行 转发,源MAC是DIP所在的接口的MAC,目标MAC是某挑选出的RS的RIP所在接口的MAC地址;源 IP/PORT…...

写给小白程序员的一封信
文章目录 1.编程小白如何成为大神?大学新生的最佳入门攻略2.程序员的练级攻略3.编程语言的选择4.熟悉Linux5.学会git6.知道在哪寻求帮助7.多结交朋友8.参加开源项目9.坚持下去 1.编程小白如何成为大神?大学新生的最佳入门攻略 编程已成为当代大学生的必…...

Leaf分布式ID
文章目录 系统对Id号的要求UUIDsnowflakeLeafLeaf-snowflakeLeaf-segmentMySQL自增主键segment双buffer 系统对Id号的要求 1、业务 1)全局唯一性:不能出现重复的ID号,既然是唯一标识,这是最基本的要求 2)趋势递增&a…...

Starrocks解析json数组
json数据 [{"spec": "70g/支","unit": "支","skuId": "1707823848651276346","amount": 6,"weight": 70,"spuName": "伊利 甄稀 苦咖啡味雪糕 流心冰淇淋 70g/支",&quo…...
安卓基本布局(下)
TableLayout 常用属性描述collapseColumns设置需要被隐藏的列的列号。shrinkColumns设置允许被伸缩的列的列号。stretchColumns设置允许被拉伸的列的列号。 <TableLayout xmlns:android"http://schemas.android.com/apk/res/android"android:id"id/TableL…...

Python中使用正则表达式
摘要: 正则表达式,又称为规则表达式,它不是某种编程语言所特有的,而是计算机科学的一个概念,通常被用来检索和替换某些规则的文本。 一.正则表达式的语法 ①行定位符 行定位符就是用来描述字符串的边界。"^&qu…...

三大口诀不一样的代码,小小的制表符和换行符玩的溜呀
# 小案例,打印输出加法口诀 for i in range(1,10):for j in range(1,10):if j>i:breakprint(f"{j}{i}{ji}".strip(),end\t)print() print(\n) for i in range(1,10):for j in range(1,10):if j>i:breakprint(f"{j}x{i}{j*i}",end\t)print…...

[qt] 线程等待与唤醒
对于生产者与消费者的数据处理的另一种好的解决方法是使用QWaitCondition类,允许线程在一定的条件下唤醒其他多个线程来共同处理。 一 定义公共变量 DataSize: 生产者生产数据的大小BufferSize: 也就是这个缓冲区的大小,每个单元是一个int,也有可能是一个链表,结构…...

Springboot 实现 Modbus Rtu 协议接入物联网设备
Modbus RTU 技术教程 引言 Modbus是一种开放标准的通信协议,它最初由Modicon(现施耐德电气)在1979年发布,旨在让可编程逻辑控制器(PLC)之间能够进行通信。随着时间的发展,Modbus已经成为工业自动化领域中最常用的通信协议之一,尤其适用于连接工业电子设备。本文将详细…...

鸿蒙笔记--装饰器
这一节主要了解一下鸿蒙里的装饰器,装饰器是一种特殊的语法结构,用于装饰类、结构体、方法以及变量; 1 Component在鸿蒙(HarmonyOS)开发中扮演着重要角色,主要用于定义可重用的UI组件,主要作用:1)组件化:Component装饰…...
不同环境下RabbitMQ的安装-3 操作RabbitMQ
前面两篇从不同环境下RabbitMQ的安装-1 为什么要使用消息服务 到同环境下RabbitMQ的安装-2 ARM架构、X86架构、Window系统环境下安装RabbitMQ介绍了关于如何在ARM架构、X86架构和Window系统下如何安装,各位小伙伴可以根据自己的实际开发场景参考安装。 到本篇是一些…...

postgregSQL配置vector插件
1.下载vector 下载vector:https://pgxn.org/dist/vector/0.5.1/ 放在:C:\Program Files\PostgreSQL\vector-0.5.1 2.安装Visual Studio 2022 下载:https://visualstudio.microsoft.com/zh-hans/downloads/ 安装Visual Studio是为了C编译环…...
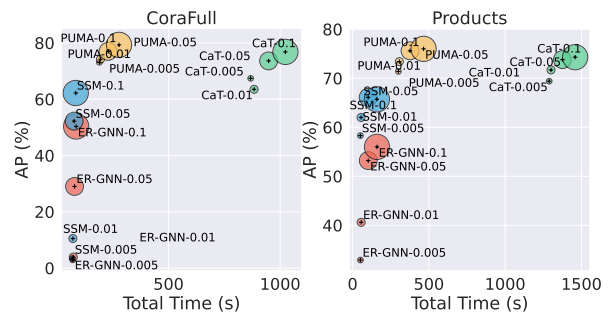
PUMA论文阅读
PUMA: Efficient Continual Graph Learning with Graph Condensation PUMA:通过图压缩进行高效的连续图学习 ABSTRACT 在处理流图时,现有的图表示学习模型会遇到灾难性的遗忘问题,当使用新传入的图进行学习时,先前学习的这些模…...
)
算法学习day31(动态规划)
一、比特位计数 给你一个整数 n ,对于 0 < i < n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n 1 的数组 ans 作为答案。 输入:n 2 输出:[0,1,1] 解释:0 --> 0 1 --> 1 2 -…...

嵌入式学Day25---Linux软件编程---线程间通信
目录 编辑 一、线程的分离属性 1.1.什么是分离属性 1.2.分离属性相关函数接口 1.初始化线程属性-pthread_attr_init() 2.销毁线程属性-pthread_attr_destory() 3.设置线程属性-pthread_setdetachstate() 1.3.注意 二、互斥锁 2.1.资源 2.2.互斥锁 1.什么是互斥锁 2.互…...

【实现100个unity特效之17】在unity中使用shader和ShaderGraph分别实现模糊特定层,高斯模糊效果
最终效果 Unity通过Shader来模糊场景画面 参考:【游戏开发小技】Unity通过UI全屏图来模糊场景画面(Shader | 模糊 | 滤镜 | Blur) ShaderGraph实现图片的高斯模糊 参考:【游戏开发实战】Unity ShaderGraph实现图片的高斯模糊效…...

Unity补完计划 之 SpriteEditer Multiple
本文仅作笔记学习和分享,不用做任何商业用途 本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 1. SpriteEditer Multiple Automatic slicing - Unity 手册 这是用于裁剪图集的模式 应用之后精灵编辑器会看到Slice亮…...

C++ IOStream
IOStream 类流特性 不可赋值和复制缓冲重载了<< >> 状态位 示例 状态位操作函数coutcin getget(s,n)/get(s,n,d):getline otherif(!fs)/while(cin) operator void*()与 operator!()代码示例 File Stream open 函数 文件打开方式 文件读写 读写接口 一次读一个字符…...

2024/8/8训练
A - 无线网络整点栅格统计 题目链接 算法:模拟 题目大意 给你一个n*m的网格,然后输出每一个点作为顶点能构成的正方形数量(可以为斜正方形). 算法思路 本身题目数据是很小的,可以通过n^2的时间复杂度枚举每一个顶点,然后再通过n平方的时间复杂度枚举出另一个对角顶点,判断…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...
