[算法] 第二集 二叉树中的深度搜索
一、计算布尔二叉树的值
1.题目描述

2.算法思路
书面解释就是:
1. 对于规模为 n 的问题,需要求得当前节点值。
2. 节点值不为 0 或 1 时,规模为 n 的问题可以被拆分为规模为 n-1 的子问题:a. 所有子节点的值;b. 通过子节点的值运算出当前节点值。
3. 当问题的规模变为 n=1 时,即叶⼦节点的值为 0 或 1,我们可以直接获取当前节点值为 0 或 1。


3.代码实现
class Solution
{
public:bool evaluateTree(TreeNode* root) {if(root->left == nullptr) {return root->val == 0 ? false : true;}bool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2 ? left | right : left & right;}
};
二、求根节点到叶节点数字之和
1.题目描述

2.算法思路
通过前序遍历,往左右子树传递信息,并且在回溯时得到左右子树的返回值。让递归函数完成两件事:1. 将父节点的数字与当前节点的信息整合到⼀起,计算出当前节点的数字,然后传递到下⼀层进行递归;2. 当遇到叶子节点的时候,就不再向下传递信息,将整合的结果向上⼀直回溯到根节点。在递归结束时,根节点需要返回的值也就被更新为了整棵树的数字和。
递归函数设计:int dfs(TreeNode* root, int num)1. 返回值:当前子树计算的结果(数字和);2. 参数 num:递归过程中往下传递的信息(父节点的数字);3. 函数作用:整合父节点的信息与当前节点的信息计算当前节点数字,并向下传递,再回溯时返回当前子树(当前节点作为子树根节点)数字和。



递归函数流程:1. 当遇到空节点的时候,说明这条路从根节点开始没有分⽀,返回 0;2. 结合⽗节点传下的信息以及当前节点的 val,计算出当前节点数字 sum;3. 如果当前结点是叶子节点,直接返回整合后的结果 sum;4. 如果当前结点不是叶父节点,将 sum 传到左右子树中去,得到左右子树中节点路径的数字和,然 后相加后返回结果。
3.代码实现
class Solution {
public:int dfs(TreeNode* root, int prevSum) {if (root == nullptr) {return 0;}int sum = prevSum * 10 + root->val;if (root->left == nullptr && root->right == nullptr) {return sum;} else {return dfs(root->left, sum) + dfs(root->right, sum);}}int sumNumbers(TreeNode* root) {return dfs(root, 0);}
};三、二叉树剪枝
1.题目描述
2.算法思路
• 需要注意的是,在删除叶子节点时,其父节点很可能会成为新的叶子节点。因此,在处理完子节点后,我们仍然需要处理当前节点。这也是为什么选择后序遍历的原因(后序遍历⾸先遍历到的一定是叶子节点)。• 通过使用后序遍历,我们可以逐步删除叶子节点,并且保证删除后的节点仍然满足删除操作的要求。这样,我们可以较为方便地实现删除操作,而不会影响最终的结果。• 若在处 理结束后所有叶子节点的值均为 1,则所有子树均包含 1,此时可以返回。
递归函数设计:void dfs(TreeNode*& root)1. 返回值:无;2. 参数 :当前需要处理的节点;3. 函数作用:判断当前节点是否需要删除,若需要删除,则删除当前节点。
1. 递归出口:当传入节点为空时,不做任何处理;2. 递归处理左子树;3. 递归处理右子树;4. 处理当前节点:判断该节点是否为叶⼦节点(即左右⼦节点均被删除,当前节点成为叶子节点),并且节点的值为 0:a. 如果是,就删除掉;b. 如果不是,就不做任何处理。
3.代码实现:
class Solution
{
public:TreeNode* pruneTree(TreeNode* root) {if(root == nullptr) return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);if(root->left == nullptr && root->right == nullptr && root->val == 0){delete root; // 防⽌内泄漏root = nullptr;}return root;}
};四、验证二叉搜索树
1.题目描述

2.算法思路
- 初始化⼀个全局的变量 prev,⽤来记录中序遍历过程中的前驱结点的 val;
- 中序遍历的递归函数中:
a. 设置递归出⼝:root == nullptr 的时候,返回 true;b. 先递归判断左⼦树是否是⼆叉搜索树,⽤ retleft 标记;c. 然后判断当前结点是否满⾜⼆叉搜索树的性质,用 retcur 标记:▪ 如果当前结点的 val ⼤于 prev,说明满足条件,retcur 改为 true;▪ 如果当前结点的 val ⼩于等于 prev,说明不满⾜条件,retcur 改为 false;d. 最后递归判断右⼦树是否是⼆叉搜索树,⽤ retright 标记;- 只有当 retleft、 retcur 和 retright 都是 true 的时候,才返回 true。
3.代码实现
class Solution
{
public:long prev = LONG_MIN;bool isValidBST(TreeNode* root) {if(root == nullptr) return true;bool left = isValidBST(root->left);// 剪枝if(left == false) return false;bool cur = false;if(root->val > prev)cur = true;// 剪枝if(cur == false) return false;prev = root->val;bool right = isValidBST(root->right);return left && right && cur;}
};感谢大家的观看,如有错误欢迎指正!
相关文章:

[算法] 第二集 二叉树中的深度搜索
深度优先遍历(DFS,全称为 Depth First Traversal),是我们树或者图这样的数据结构中常⽤的 ⼀种遍历算法。这个算法会尽可能深的搜索树或者图的分支,直到⼀条路径上的所有节点都被遍历 完毕,然后再回溯到上…...

放弃使用外键时,sequelize 应该怎么使用?
在使用 Sequelize 时,如果想放弃使用外键,但仍然希望在模型之间建立关联,可以通过设置 constraints 选项为 false 来实现。这允许你定义模型之间的关系,而不在数据库中创建外键约束。以下是具体的实现步骤: 定义没有外…...

Microsoft GraphRAG 输出的配置信息
Microsoft GraphRAG 输出的配置信息 {"llm": {"api_key": "REDACTED, length 9","type": "oci_genai_chat","model": "cohere.command-r-plus","max_tokens": 4000,"temperature"…...

怎么判断张量的维度(形状(shape)),即如何定义行数、列数和深度的?
举一个三维张量吧 # 3行4列深度为2 const3 tf.constant([[[1,2],[3,4],[5,6],[7,8]],[[11, 12], [13, 14], [15, 16], [17, 18]],[[21, 22], [23, 24], [25, 26], [27, 28]] ],tf.float16) shape (3,4,2)--借鉴博主奶油松果的图和代码 分析形状 (3, 4, 2) 最外层的括号&…...

AI入门指南(二):算法、训练、模型、大模型是什么?
文章目录 一、前言二、算法是什么?概念实际应用 三、训练是什么?概念实际应用 四、模型是什么?概念实际应用小结 五、大模型是什么?概念大模型和小模型有什么区别?大模型分类实际应用 六、总结七、参考资料 一、前言 …...

CSS已访问链接的隐私保护
摘抄自:《CSS权威指南 第四版》 有超过十年的时间,已访问的链接可以使用任何可用的CSS属性装饰,与未访问链接没有差别。 然而,大约在2005年,有几个人通过示例揭露,通过视觉样式和简单的DOM脚本就可以判断用…...

代码练习12-排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 归并排序算法核心步骤 归并排序核心步骤如下: 把长度为n的要排序的序列,分成两个长度为n/2的子序列;对这两个子序列,分别采用归并排序;…...

Linux 内核源码分析---套接字
套接字通信 ISO 设计一种参考模型,定义组成网络的各个层,该模型由7层组成,称为OSI(开放 系统互连)模型如下: 应用层:网络服务与最终用户的接口; 表示层:数据的表示、安…...
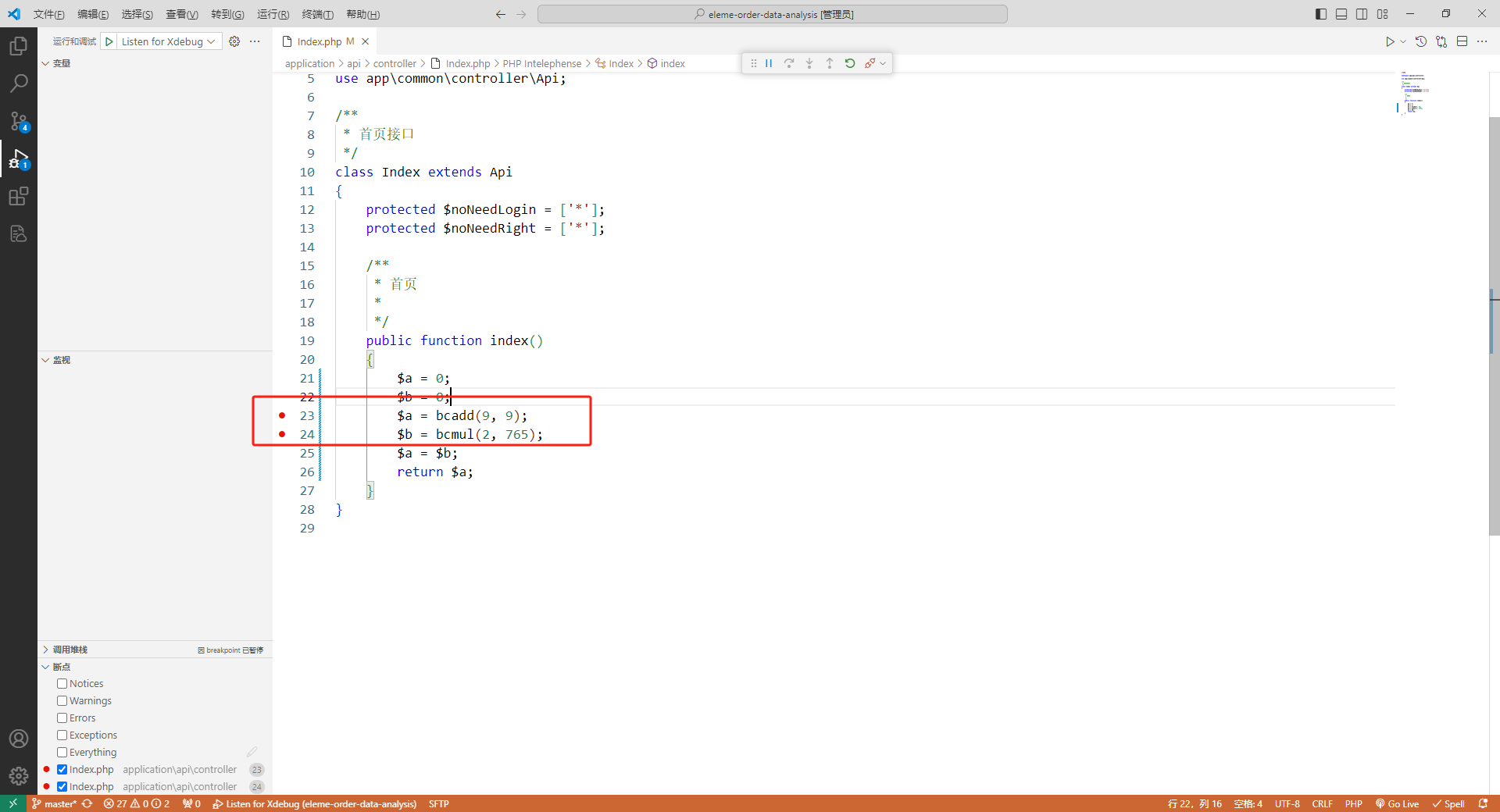
vscode配置xdebug断点调试详细教程
注:环境为本地windows开发环境,编辑器为vscode,PHP集成环境工具为EServer vscode安装扩展并配置 安装PHP Debug 扩展中搜索 PHP Debug 并安装: 配置PHP Debug 1、点击扩展设置 2、在设置中,点击 setting.json 3、编…...

【人工智能】Transformers之Pipeline(八):文生图/图生图(text-to-image/image-to-image)
目录 一、引言 二、文生图/图生图(text-to-image/image-to-image) 2.1 文生图 2.2 图生图 2.3 技术原理 2.3.1 Diffusion扩散模型原理 2.3.2 Stable Diffusion扩散模型原理 2.4 文生图实战 2.4.1 SDXL 1.0 2.4.2 SD 2.0 2.5 模型排名 三、总…...

AI Agent 工程师认证-学习笔记(1)——【单Agent】ModelScope-Agent
学习链接: 【单Agent】ModelScope-Agent学习指南https://datawhaler.feishu.cn/wiki/GhOLwvAPkiSWmokjUgqc1eGonDf 手把手Agent开发开源教程(觉得不错的话可以star一下)https://github.com/datawhalechina/agent-tutorial 动手学Agent应用…...

【Python机器学习】树回归——将CART算法用于回归
要对数据的复杂关系建模,可以借用树结构来帮助切分数据,如何实现数据的切分?怎样才能知道是否已经充分切分?这些问题的答案取决于叶节点的建模方式。回归树假设叶节点是常数值,这种策略认为数据中的复杂关系可以用树结…...

前端(HTML + CSS)小兔鲜儿项目(仿)
前言 这是一个简单的商城网站,代码部分为HTML CSS 和少量JS代码 项目总览 一、头部区域 头部的 购物车 和 手机 用的是 文字图标,所以效果可以和文字一样 购物车右上角用的是绝对定位 logo用的是 h1 标签,用来提高网站搜索排名 二、banne…...

【Rust光年纪】构建高效终端用户界面:Rust库全面解析
构建优雅终端应用:深度评析六大Rust库 前言 随着Rust语言的流行和应用场景的不断扩大,对于终端操作和用户界面构建的需求也日益增长。本文将介绍一些在Rust语言中常用的终端操作库和用户界面构建库,以及它们的核心功能、使用场景、安装与配…...
)
鼠标滑动选中表格部分数据列(vue指令)
文章目录 代码指令代码使用代码 代码 指令代码 // 获得鼠标移动的范围 function getMoveRange(startClientX, endClientX, startClientY, endClientY) {const _startClientX Math.min(startClientX, endClientX);const _endClientX Math.max(startClientX, endClientX);con…...

“5G+Windows”推动全场景数字化升级:美格智能5G智能模组SRM930成功运行Windows 11系统
操作系统作为连接用户与数字世界的桥梁,在数字化迅速发展的时代扮演着至关重要的角色,智能设备与操作系统的协同工作,成为推动现代生活和商业效率的关键力量。其中,Windows系统以其广泛的应用基础和强大的兼容性成为全球最广泛使用…...

c语言学习,isupper()函数分析
1:isupper() 函数说明: 检查参数c,是否为大写英文字母。 2:函数原型: int isupper(int c) 3:函数参数: 参数c,为检测整数 4:返回值: 参数c是大写英文字母&…...

Adnroid 数据存储:SharedPreferences详解【SharedPreferencesUtils,SharedPreferences的ANR】
目录 1)SP是什么、如何使用,SPUtils 2)SP的流程 3)comit和apply 一、SP是什么,如何使用,SPUtils 1.1 SP是什么? SharedPreferences是Android平台提供的一种轻量级的数据存储方式,…...

Sentinel 规则持久化到 Nacos 实战
前言: 前面系列文章我们对 Sentinel 的作用及工作流程源码进行了分析,我们知道 Sentinel 的众多功能都是通过规则配置完成的,但是我们前面在演示的时候,发现 Sentinel 一重启,配置的规则就没有了,这是因为…...
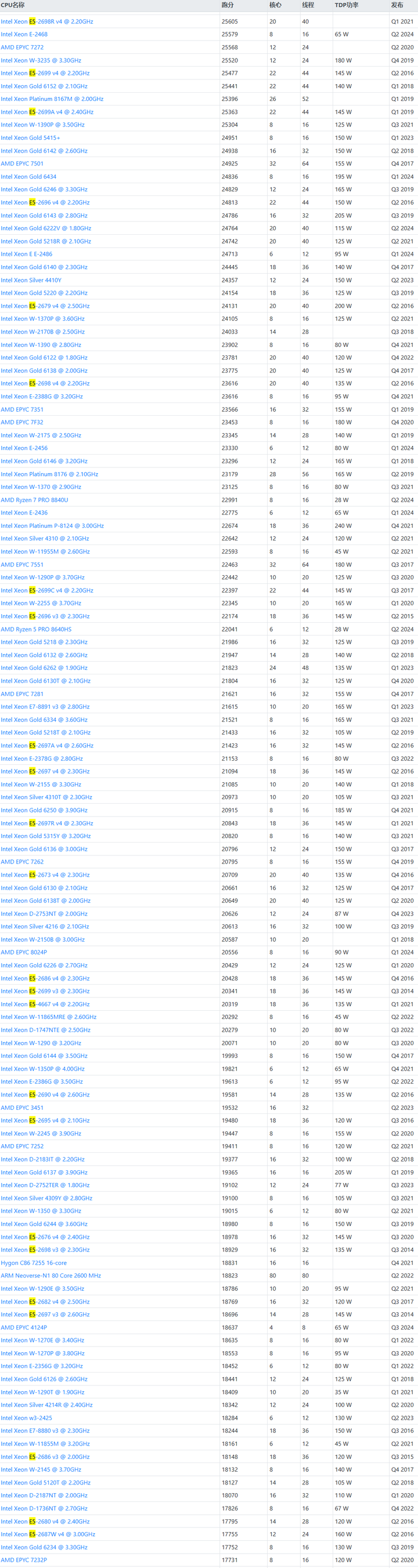
服务器CPU天梯图2024年8月,含EYPC/至强及E3/E5
原文地址(高清无水印原图/持续更新/含榜单出处链接): >>>服务器CPU天梯图<<< 本文提供的服务器CPU天梯图数据均采集自各大专业网站,榜单图片末尾会标准其来源(挂太多链接有概率会被ban,…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
