怎么判断张量的维度(形状(shape)),即如何定义行数、列数和深度的?
举一个三维张量吧
# 3行4列深度为2
const3 = tf.constant([[[1,2],[3,4],[5,6],[7,8]],[[11, 12], [13, 14], [15, 16], [17, 18]],[[21, 22], [23, 24], [25, 26], [27, 28]]
],tf.float16)
shape = (3,4,2)

--借鉴博主奶油松果的图和代码
分析形状 (3, 4, 2)
-
最外层的括号(第一个维度):
const3包含了三个子列表:[[1, 2], [3, 4], [5, 6], [7, 8]][[11, 12], [13, 14], [15, 16], [17, 18]][[21, 22], [23, 24], [25, 26], [27, 28]]
- 因此,第一个维度的大小是
3,这代表张量的行数。
-
第二层的括号(第二个维度):
- 每个子列表又包含四个小列表:
[1, 2],[3, 4],[5, 6],[7, 8][11, 12],[13, 14],[15, 16],[17, 18][21, 22],[23, 24],[25, 26],[27, 28]
- 因此,第二个维度的大小是
4,这代表每行的列数。
- 每个子列表又包含四个小列表:
-
最内层的括号(第三个维度):
- 每个小列表包含两个元素:
[1, 2][11, 12][21, 22]
- 因此,第三个维度的大小是
2,这代表每个元素的深度。 可以看上边引用的图 的确是这样的哦
- 每个小列表包含两个元素:
形象化理解
可以把这个张量想象成一本书:
- 书本有3页(行数 = 3)
- 每页有4个段落(列数 = 4)
- 每个段落有2个句子(深度 = 2)
所以,整个张量的形状是 (3, 4, 2)。
TRM
理解TRM中的 unsqueeze(1)了没,第二个维度(维度1)加上一列,那就是每个子列表里 又包含1个小列表
最外层的括号(第一个维度):
const3包含了2个子列表: 那就是每个子列表里 又包含1个小列表 每个小列表包含5个元素

相关文章:

怎么判断张量的维度(形状(shape)),即如何定义行数、列数和深度的?
举一个三维张量吧 # 3行4列深度为2 const3 tf.constant([[[1,2],[3,4],[5,6],[7,8]],[[11, 12], [13, 14], [15, 16], [17, 18]],[[21, 22], [23, 24], [25, 26], [27, 28]] ],tf.float16) shape (3,4,2)--借鉴博主奶油松果的图和代码 分析形状 (3, 4, 2) 最外层的括号&…...

AI入门指南(二):算法、训练、模型、大模型是什么?
文章目录 一、前言二、算法是什么?概念实际应用 三、训练是什么?概念实际应用 四、模型是什么?概念实际应用小结 五、大模型是什么?概念大模型和小模型有什么区别?大模型分类实际应用 六、总结七、参考资料 一、前言 …...

CSS已访问链接的隐私保护
摘抄自:《CSS权威指南 第四版》 有超过十年的时间,已访问的链接可以使用任何可用的CSS属性装饰,与未访问链接没有差别。 然而,大约在2005年,有几个人通过示例揭露,通过视觉样式和简单的DOM脚本就可以判断用…...

代码练习12-排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 归并排序算法核心步骤 归并排序核心步骤如下: 把长度为n的要排序的序列,分成两个长度为n/2的子序列;对这两个子序列,分别采用归并排序;…...

Linux 内核源码分析---套接字
套接字通信 ISO 设计一种参考模型,定义组成网络的各个层,该模型由7层组成,称为OSI(开放 系统互连)模型如下: 应用层:网络服务与最终用户的接口; 表示层:数据的表示、安…...
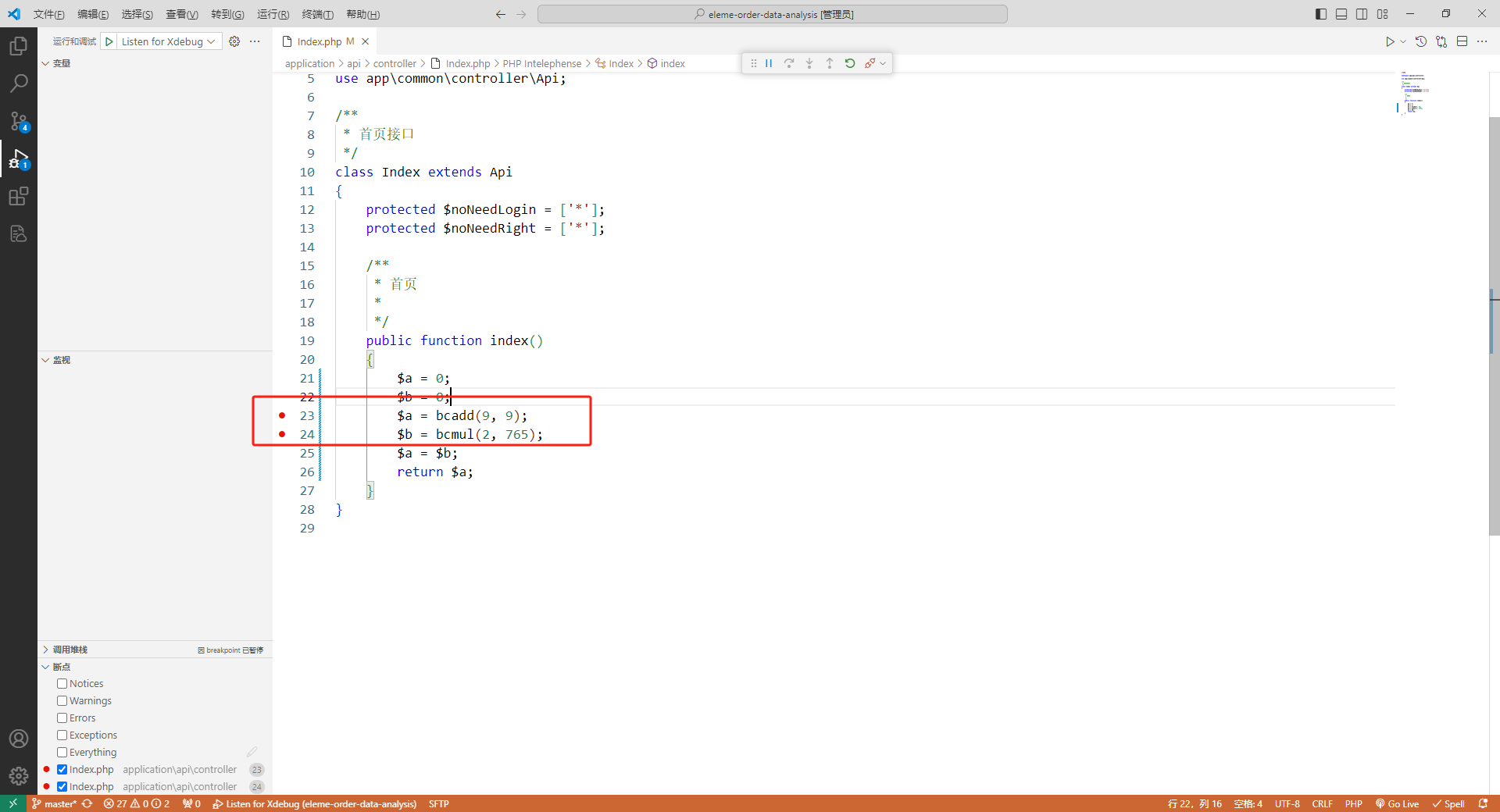
vscode配置xdebug断点调试详细教程
注:环境为本地windows开发环境,编辑器为vscode,PHP集成环境工具为EServer vscode安装扩展并配置 安装PHP Debug 扩展中搜索 PHP Debug 并安装: 配置PHP Debug 1、点击扩展设置 2、在设置中,点击 setting.json 3、编…...

【人工智能】Transformers之Pipeline(八):文生图/图生图(text-to-image/image-to-image)
目录 一、引言 二、文生图/图生图(text-to-image/image-to-image) 2.1 文生图 2.2 图生图 2.3 技术原理 2.3.1 Diffusion扩散模型原理 2.3.2 Stable Diffusion扩散模型原理 2.4 文生图实战 2.4.1 SDXL 1.0 2.4.2 SD 2.0 2.5 模型排名 三、总…...

AI Agent 工程师认证-学习笔记(1)——【单Agent】ModelScope-Agent
学习链接: 【单Agent】ModelScope-Agent学习指南https://datawhaler.feishu.cn/wiki/GhOLwvAPkiSWmokjUgqc1eGonDf 手把手Agent开发开源教程(觉得不错的话可以star一下)https://github.com/datawhalechina/agent-tutorial 动手学Agent应用…...

【Python机器学习】树回归——将CART算法用于回归
要对数据的复杂关系建模,可以借用树结构来帮助切分数据,如何实现数据的切分?怎样才能知道是否已经充分切分?这些问题的答案取决于叶节点的建模方式。回归树假设叶节点是常数值,这种策略认为数据中的复杂关系可以用树结…...

前端(HTML + CSS)小兔鲜儿项目(仿)
前言 这是一个简单的商城网站,代码部分为HTML CSS 和少量JS代码 项目总览 一、头部区域 头部的 购物车 和 手机 用的是 文字图标,所以效果可以和文字一样 购物车右上角用的是绝对定位 logo用的是 h1 标签,用来提高网站搜索排名 二、banne…...

【Rust光年纪】构建高效终端用户界面:Rust库全面解析
构建优雅终端应用:深度评析六大Rust库 前言 随着Rust语言的流行和应用场景的不断扩大,对于终端操作和用户界面构建的需求也日益增长。本文将介绍一些在Rust语言中常用的终端操作库和用户界面构建库,以及它们的核心功能、使用场景、安装与配…...
)
鼠标滑动选中表格部分数据列(vue指令)
文章目录 代码指令代码使用代码 代码 指令代码 // 获得鼠标移动的范围 function getMoveRange(startClientX, endClientX, startClientY, endClientY) {const _startClientX Math.min(startClientX, endClientX);const _endClientX Math.max(startClientX, endClientX);con…...

“5G+Windows”推动全场景数字化升级:美格智能5G智能模组SRM930成功运行Windows 11系统
操作系统作为连接用户与数字世界的桥梁,在数字化迅速发展的时代扮演着至关重要的角色,智能设备与操作系统的协同工作,成为推动现代生活和商业效率的关键力量。其中,Windows系统以其广泛的应用基础和强大的兼容性成为全球最广泛使用…...

c语言学习,isupper()函数分析
1:isupper() 函数说明: 检查参数c,是否为大写英文字母。 2:函数原型: int isupper(int c) 3:函数参数: 参数c,为检测整数 4:返回值: 参数c是大写英文字母&…...

Adnroid 数据存储:SharedPreferences详解【SharedPreferencesUtils,SharedPreferences的ANR】
目录 1)SP是什么、如何使用,SPUtils 2)SP的流程 3)comit和apply 一、SP是什么,如何使用,SPUtils 1.1 SP是什么? SharedPreferences是Android平台提供的一种轻量级的数据存储方式,…...

Sentinel 规则持久化到 Nacos 实战
前言: 前面系列文章我们对 Sentinel 的作用及工作流程源码进行了分析,我们知道 Sentinel 的众多功能都是通过规则配置完成的,但是我们前面在演示的时候,发现 Sentinel 一重启,配置的规则就没有了,这是因为…...
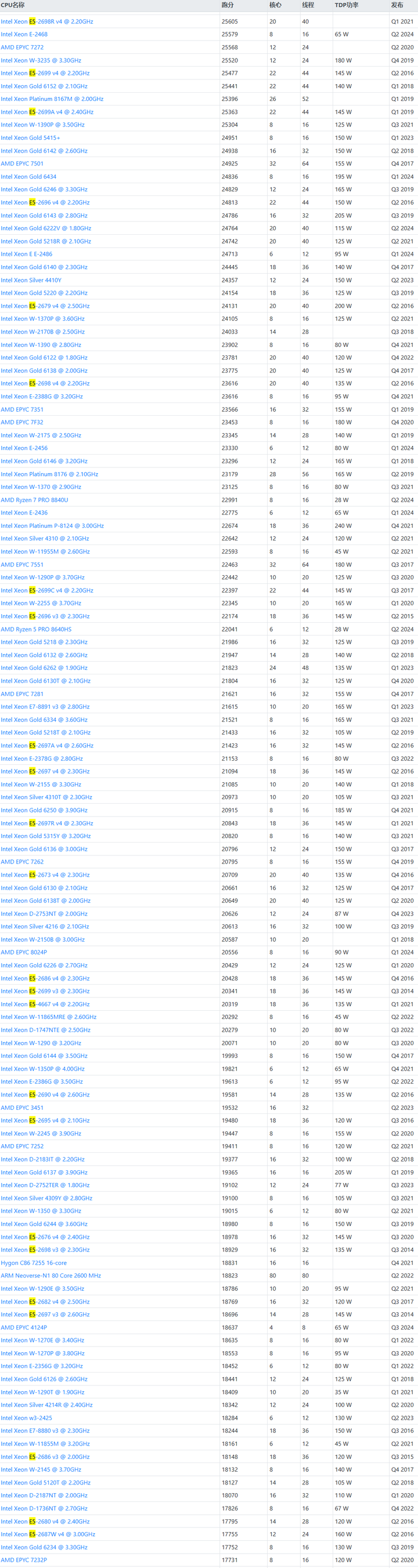
服务器CPU天梯图2024年8月,含EYPC/至强及E3/E5
原文地址(高清无水印原图/持续更新/含榜单出处链接): >>>服务器CPU天梯图<<< 本文提供的服务器CPU天梯图数据均采集自各大专业网站,榜单图片末尾会标准其来源(挂太多链接有概率会被ban,…...

SpringBoot加载dll文件示例
1、将动态库放在resource文件目录下 2、编写相关加载逻辑 import lombok.extern.slf4j.Slf4j; import java.io.File; import java.io.IOException; import java.lang.reflect.Field; import java.util.HashMap;/*** Description: 加载动态库 .dll文件* author: Be.insighted* c…...

9.C基础_指针与数组
数组指针(一维数组) 数组指针就是" 数组的指针 ",它是一个指向数组首地址的指针变量。 1、数组名的含义 对于一维数组,数组名就是一个指针,指向数组的首地址。 基于如下代码进行分析: int a…...

C语言——结构体与共用体
C语言——结构体与共用体 结构体共用体 结构体 如果将复杂的复杂的数据类型组织成一个组合项,在一个组合项中包含若干个类型不同(当然也可以相同)的数据项。 C语言允许用户自己指定这样一种数据结构,它称为结构体。 结构体的语法…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...
