github技巧和bug解决方法短篇收集
有一些几句话就可以说明白的观点或者解决的的问题,小虎单独收集到这里。
Commits没有算入每天的activity
fork的仓库是不算的。
Commits made in a fork will not count toward your contributions.
参考:
Contribution activity not shown for github page
移除已忽略的文件Remove ignored file in .gitignore
The rules in your .gitignore file only apply to untracked files. Since the files under that directory were already committed in your repository, you have to unstage them, create a commit, and push that to GitHub:
git rm -r --cached your_file
git commit -m 'Remove the now ignored file'
git push origin master
参考:
https://stackoverflow.com/a/7927283/15329637
引用github仓库Cite github repo

参考:
https://academia.stackexchange.com/questions/14010/how-do-you-cite-a-github-repository
github仓库数据查看Github repo data

相关文章:

github技巧和bug解决方法短篇收集
有一些几句话就可以说明白的观点或者解决的的问题,小虎单独收集到这里。 Commits没有算入每天的activity fork的仓库是不算的。 Commits made in a fork will not count toward your contributions. 参考: Contribution activity not shown for github…...

学习笔记五:在k8s中安装EFK组件(elasticsearch+fluentd+kibana)
在k8s 1.3安装EFK组件 前置条件上传压缩包安装nfs供应商创建nfs作为存储的供应商通过deployment创建pod用来运行nfs-provisioner 安装elasticsearch组件安装kibana组件安装fluentd组件 前置条件 查看k8s版本 kubectl get node -owide相关安装包 链接:https://pan.ba…...

Golang编译-如何忽略某些文件去编译
在 Go 语言中,编译好的二进制文件不会被再次加入到编译过程中。Go 编译器只会编译源代码文件(如 .go 文件),而不会将已经编译好的二进制文件(如可执行文件或静态库)作为输入来进行编译。 详细解释…...
有哪些适合中型企业的人力资源管理系统推荐?
本文主要介绍了以下几款人力资源管理系统:Moka、OrangeHRM、Verint、希沃人事、UKG Pro、大易Dayee、DingTalk、致远OA、卓望ShineHR、GoCo。 在选择人力资源管理系统时,中型企业面临着诸多挑战:如何确保系统既能满足现有需求,又能…...

活动回顾|首次 Cloudberry Database Meetup · 北京站成功举办
8 月 3 日,由酷克数据 HashData 主办的 Cloudberry Database Meetup 北京站活动圆满结束。本次 Meetup 以“以开源应对 Greenplum 闭源,原厂开发者再聚首”为主题,深入探讨了 Greenplum 闭源所带来的影响,并聚焦于 Cloudberry Dat…...

C语言 软件设计的七大原则,及其应用案例
1. 单一职责原则 (Single Responsibility Principle, SRP) 定义: 一个模块或函数应当只有一个引起变化的原因。 应用案例: 在嵌入式系统中,可以将传感器数据的读取和处理分开成不同的函数。例如: // 读取传感器数据的函数 floa…...

初学嵌入式-C语言常犯错误详解
1、对于下面这道题,估计有很多人会选择B答案,但其实答案是D 2.int a10, b9,c9,d; d b || (a>c),请问上述代码执行完毕后a b c d的值分别是 。 A、10 9 10 9 B、10 10 10 1 C、10 9 10 1 D、10 10 9 1 答案解释: 在C语言…...
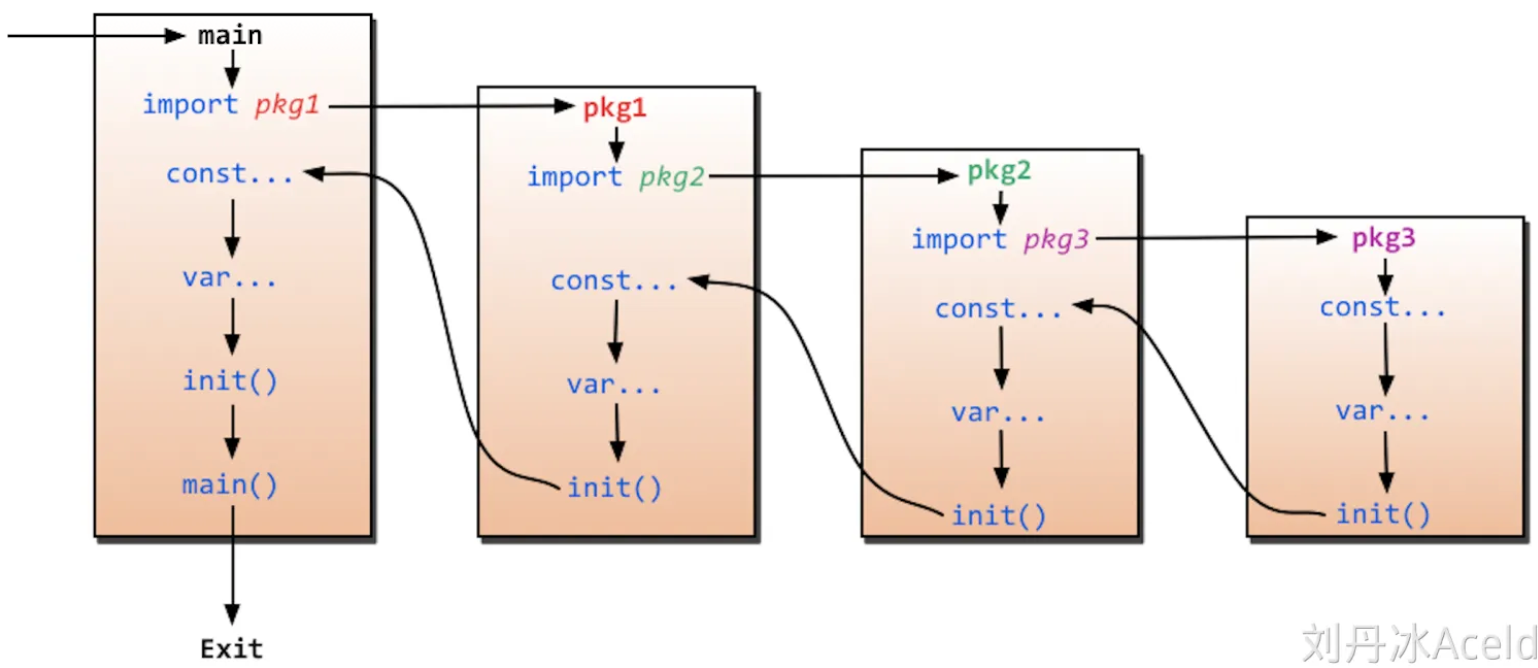
Golang 语法入门
Golang 语法入门 Hello World package mainimport "fmt"func main() {fmt.Println("hello world") }变量 package mainimport "fmt"// 全局变量 var ans 123 var cnt intfunc main() {// 单个局部变量a : 114514// 多个局部变量b, c : 114, …...

Filebeat+Kafka+ELK
架构: 部署: #配置nginx,部署filebeat systemctl stop firewalld setenforce 0 systemctl restart nginx#解压filebeat tar -xf filebeat-6.7.2-linux-x86_64.tar.gz mv filebeat-6.7.2-linux-x86_64 filebeat#日志收集 cd firebeat vim fil…...

Python 为Excel单元格设置填充\背景色 (纯色、渐变、图案)
在使用Excel进行数据处理和分析时,对特定单元格进行背景颜色填充不仅能够提升工作表的视觉吸引力,还能帮助用户快速识别和区分不同类别的数据,增强数据的可读性和理解性。 本文将通过以下三个示例详细介绍如何使用Python在Excel中设置不同的单…...

家里浮毛粉尘到处飞?宠物空气净化器出动帮你解决
由于家里收养的十几只流浪猫咪夏季掉毛非常严重,整个房子弥漫着猫毛,而且这十几只里面有七八只还是长毛的品种,掉落的毛发都因为太长而直接掉落成毛团,而短毛的那几只也在掉毛,这十几只掉下的浮毛,家里已经…...

计算机网络ISO七层网络模型及TCP
思维导图(通俗理解) 首先,先用最通俗的话来描述ISO七层模型,思维导图结构如下: ISO七层网络模型概念 应用层(Application Layer):应用层是OSI模型的最高层,直接与用户交…...

机器学习知识点全面总结
一、机器学习基础概念 1、什么是机器学习 机器学习是一种人工智能技术,通过对数据的学习和分析,让计算机系统自动提高其性能。简而言之,机器学习是一种从数据中学习规律和模式的方法,通过数据来预测、分类或者决策。 机器学习的本…...

【研发日记】嵌入式处理器技能解锁(三)——TI C2000 DSP的C28x内核
文章目录 前言 背景介绍 C28x内核 浮点单元(FPU) 快速整数除法单元(FINTDIV) 三角数学单元(TMU) VCRC单元 CPU总线 指令流水线 总结 参考资料 前言 见《【研发日记】嵌入式处理器技能解锁(一)——多任务异步执行调度的三种方法》 见《【研发日记】嵌入式处理器技能解…...

LeetCode.27.移除元素
题目描述: 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。 假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以…...
可重入锁总结)
redis面试(十二)可重入锁总结
可重入锁总结 从实现原理以及源码的层面,真正剖析和了解到了redis分布式锁的企业级的实现,这个分布式锁实现的还是非常漂亮的,麻雀虽小,五脏俱全,分布式的可重入锁,总结一下流程 (1࿰…...

软件测试知识点3
063、一份测试计划应该包括哪些内容? 背景、项目简介、目的、测试范围、测试策略、人员分工、资源要求、进度计划、参考文档、常用术语、提交文档、风险分析。 065、如何定位测试用例的作用? 组织性:编写、组织性、功能覆盖、重复性、跟踪、测试确认 066、什么…...

WPF Treeview开启虚拟化后如何找到TreeViewItem
用VirtualizingStackPanel的BringIndexIntoViewPublic方法就好,没必要像微软给的例子那样还要继承一个VirtualizingStackPanel /// <summary> /// Recursively search for an item in this subtree. /// </summary> /// <param name"container…...

给python初学者的一些建议
写在开篇 关于Python,可以这么说,这几年借着数据科学、机器学习与人工智能的东风,Python 老树开新花,在风口浪尖上居高不下。 Python 之所以这么受大家的青睐,是因为它语言简洁,上手容易,让非…...

【Python学习手册(第四版)】学习笔记17-作用域
个人总结难免疏漏,请多包涵。更多内容请查看原文。本文以及学习笔记系列仅用于个人学习、研究交流。 本文介绍Python作用域,介绍了变量名解析的LEGB原则,以及内置作用域,全局作用域global语句,嵌套作用域及nonlocal语…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
