LeetCode 1012. Numbers With Repeated Digits【数位DP,数学】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
Given an integer n, return the number of positive integers in the range [1, n] that have at least one repeated digit.
Example 1:
Input: n = 20
Output: 1
Explanation: The only positive number (<= 20) with at least 1 repeated digit is 11.
Example 2:
Input: n = 100
Output: 10
Explanation: The positive numbers (<= 100) with atleast 1 repeated digit are 11, 22, 33, 44, 55, 66, 77, 88, 99, and 100.
Example 3:
Input: n = 1000
Output: 262
Constraints:
1 <= n <= 10^9
题意:给定正整数 n,返回在 [1, n] 范围内具有 至少 1 位 重复数字的正整数的个数。
解法 状压+记忆化搜索(数位DP)
相似题目(基本可用通用数位DP模板来解决,但233和17.06可直接用计数原理解决,更简单):
- 233. 数字 1 的个数(题解:[[LeetCode 233. Number of Digit One【计数模拟】困难]])
- 面试题 17.06. 2出现的次数(题解:[[LeetCode 面试题 17.06. 2出现的次数【数位DP,计数原理】困难]])
- 600. 不含连续1的非负整数
- 902. 最大为 N 的数字组合
- 1067. 范围内的数字计数
- 1397. 找到所有好字符串(有难度,需要结合一个经典字符串算法)
- 更多题目见大佬[灵茶山艾府]模板库中的 dp.go。
用二进制表示集合,二进制从低到高第 iii 位为 111 、表示 iii 在集合中,为 000 表示 iii 不在集合中。
。设集合对应的二进制数为 xxx ,两个位运算操作如下:
- 判断元素 ddd 是否在集合中:
x >> d & 1可以取出 xxx 的第 ddd 个比特位,如果是 111 就说明 ddd 在集合中。 - 把元素 ddd 添加到集合中:将
x更新为x | (1 << d)。
求至少有一个重复数位的数字个数有点难,不如正难则反,转换成求无重复数位数字的个数。答案等于 nnn 减去无重复数字的个数。将 nnn 转换成字符串 sss ,定义 f(i,mask,isNum,isLimit)f(i,\textit{mask}, \textit{isNum},\textit{isLimit})f(i,mask,isNum,isLimit) 表示构造第 iii 位及其之后数位的合法方案数,参数的含义为:
- iii 表示从第 iii 位开始填数字,数位DP通用模板必备参数!
- mask\textit{mask}mask 表示前面选过的数字集合,换句话说,第 iii 位要选的数字不能在 mask\textit{mask}mask 中,这是为选出无重复数字做准备。
- isNum\textit{isNum}isNum 表示 iii 前面的数位是否填了数字。若为假表示前面没填数字,则当前位可以不填数字,或者要填入的数字至少为 111 ;若为真表示前面填了数字,则必须要填入从 000 开始的数字。例如 n=123n=123n=123 ,在 i=0i=0i=0 时跳过不填,相当于后面要构造的是一个 999999 以内的数字了,如果 i=1i=1i=1 不跳过,那么相当于构造一个 101010 到 999999 的两位数,如果 i=1i=1i=1 跳过,相当于构造的是一个 999 以内的数字。其实是统一的,isNumisNumisNum 为假时当前位可填 000(不填数字)或 111 及以上(填数字),为真时必须填从 000 开始的数字。isNumisNumisNum 的真实用处在于递归结束时判断填成的数是否不为0(全跳过或者说全填 000 就是 000 ,不能算有重复数位)。
- isLimit\textit{isLimit}isLimit 表示当前是否受到了 nnn 的约束(即要构造的数字不能超过 nnn**)。若为真,则第 iii 位填入的数字至多为 s[i]s[i]s[i] ,否则可以是 999** 。数位DP通用模板必备参数!如果在受到约束的情况下填了 s[i]s[i]s[i] ,那么后续填入的数字仍会受到 nnn 的约束。例如 n=123n=123n=123 ,那么 i=0i=0i=0 填的是 111 的话,i=1i=1i=1 的这一位至多填 222 。
实现细节如下:
- 递归入口
f(0, 0, true, false)表示:- 从 s[0]s[0]s[0] 开始枚举;
- 一开始集合中没有数字;
- 一开始要受到 nnn 的约束(否则就可以随意填了,这肯定不行);
- 一开始没有填数字。
- 递归中:
- 如果 isNum\textit{isNum}isNum 为假,说明前面没有填数字,那么当前也可以不填数字,一旦从这里递归下去,isLimit\textit{isLimit}isLimit 就可以置为
false了,因为前面的高位不填数字,后面无论怎么填都比 nnn 小。 - 如果 isNum\textit{isNum}isNum 为真,那么当前必须填一个数字。枚举填入的数字,要根据 isNum\textit{isNum}isNum 和 isLimit\textit{isLimit}isLimit 来决定填入数字的范围。
- 填了数字后,从这里递归下去,isNumisNumisNum 置为真,且看情况决定 isLimitisLimitisLimit 的值——如果现在的 isLimitisLimitisLimit 为假,则递归下去也是假;如果现在的 isLimitisLimitisLimit 为真,但填的数字小于 s[i]s[i]s[i] ,则要将 isLimitisLimitisLimit 置为假递归下去,否则后面的 isLimitisLimitisLimit 仍为真。
- 如果 isNum\textit{isNum}isNum 为假,说明前面没有填数字,那么当前也可以不填数字,一旦从这里递归下去,isLimit\textit{isLimit}isLimit 就可以置为
- 递归终点:当 iii 等于 sss 长度时,如果 isNum\textit{isNum}isNum 为真,则表示得到了一个合法数字(因为不合法的不会继续递归下去),返回 111 (即一个方案),否则返回 000 。
class Solution {
public:int numDupDigitsAtMostN(int n) {string s = to_string(n);// f(i,mask,isNum,isLimit)表示计算第i位及以后的合法方案数// 这里先计算无重复数字的正整数的个数,因此用mask表示已经使用了哪些数字// isNum则表示前面是否是数字,即前面填了数字没有,填了前面就是数字为true,否则前面不是数字为false// isLimit表示是否受到了n的约束,为true表示受到n的约束,即第i位填的数<=s[i];为false表示不受到s[i]约束,最大能填9// isNum为true,前面填了数字,则这里必须填数字,从0开始,看是否受到限制来填数字// isNum为false,前面没填数字,则这里也可不填数字,此后isNum还是false,isLimit为false(因为前面必小于s[i]前面);或者从1填起来,看是否受到限制来填数字// 填数字后,isNum变为true,看情况决定isLimit是否为true(现在受到限制&&填的数字是否等于s[i])// 如果现在不受限制,以后也不受限制;如果现在受限制,但填的数小于s[i],则后面不受限制;否则后面要受到限制int m = s.size(), dp[m][1 << 10][2][2];memset(dp, -1, sizeof(dp));function<int(int, int, bool, bool)> f = [&](int i, int mask, bool isNum, bool isLimit) -> int {if (i >= m) return isNum; // 为true表示是一个合法数字,否则不是if (dp[i][mask][isNum][isLimit] != -1)return dp[i][mask][isNum][isLimit];int ans = 0;if (!isNum) // 当前数位可以不填数字ans += f(i + 1, mask, false, false); // 后面不受限制了// 下面开始填数字int lower = isNum ? 0 : 1, upper = isLimit ? s[i] - '0' : 9;for (int d = lower; d <= upper; ++d) // 枚举要填入的数字if ((mask >> d & 1) == 0) // i前面没有使用,这里可用ans += f(i + 1, mask | (1 << d), true, isLimit && d == upper);// 当前位填数字和不填数字得到的合法方案数都考虑了return dp[i][mask][isNum][isLimit] = ans;};return n - f(0, 0, false, true);}
};
大佬的解答:
问:记忆化四个状态有点麻烦,能不能只记忆化 (i,mask)(i,\textit{mask})(i,mask) 这两个状态?
答:是可以的。比如 n=234n=234n=234 ,第一位填 222 ,第二位填 333 ,后面无论怎么递归,都不会再次递归到第一位填 222 ,第二位填 333 的情况,所以不需要记录。又比如,第一位不填,第二位也不填,后面无论怎么递归也不会再次递归到这种情况,所以也不需要记录。
根据这个例子,我们可以只记录不受到 isLimit\textit{isLimit}isLimit 或 isNum\textit{isNum}isNum 约束时的状态 (i,mask)(i,\textit{mask})(i,mask) 。比如 n=234n=234n=234 ,第一位(最高位)填的 111 ,那么继续递归,后面就可以随便填,所以状态 (1,2)(1,2)(1,2) 就表示前面填了一个 111(对应的 mask\textit{mask}mask ),从第二位往后随便填的方案数。问:isNum\textit{isNum}isNum 这个参数可以去掉吗?
答:对于本题是可以的。由于 mask\textit{mask}mask 中记录了数字,可以通过判断 mask\textit{mask}mask 是否为 000 来判断前面是否填了数字,所以 isNum\textit{isNum}isNum 可以省略。代码保留了 isNum\textit{isNum}isNum ,主要是为了方便大家掌握这个模板。因为有些题目不需要 mask\textit{mask}mask ,但需要 isNum\textit{isNum}isNum 。问:能不能只记忆化 iii ?
答:这是不行的。想一想,我们为什么要用记忆化?如果递归到同一个状态时,计算出的结果是一样的,那么第二次递归到同一个状态,就可以直接返回第一次计算的结果了。通过保存第一次计算的结果,来优化时间复杂度。
由于前面选的数字会影响后面选的数字,两次递归到相同的 iii ,如果前面选的数字不一样,计算出的结果就可能是不一样的。如果只记忆化 iii ,就可能会算出错误的结果。
也可以这样理解:记忆化搜索要求递归函数无副作用(除了修改 dpdpdp 数组),从而保证递归到同一个状态时,计算出的结果是一样的。
class Solution {
public:int numDupDigitsAtMostN(int n) {string s = to_string(n);int m = s.size(), dp[m][1 << 10];memset(dp, -1, sizeof(dp));function<int(int, int, bool, bool)> f = [&](int i, int mask, bool isNum, bool isLimit) -> int {if (i >= m) return isNum; // 为true表示是一个合法数字,否则不是if (isNum && !isLimit && dp[i][mask] != -1)return dp[i][mask];int ans = 0;if (!isNum) // 当前数位可以不填数字ans += f(i + 1, mask, false, false); // 后面不受限制了// 下面开始填数字int lower = isNum ? 0 : 1, upper = isLimit ? s[i] - '0' : 9;for (int d = lower; d <= upper; ++d) // 枚举要填入的数字if ((mask >> d & 1) == 0) // i前面没有使用,这里可用ans += f(i + 1, mask | (1 << d), true, isLimit && d == upper);if (isNum && !isLimit)dp[i][mask] = ans;// 当前位填数字和不填数字得到的合法方案数都考虑了return ans;};return n - f(0, 0, false, true);}
};
复杂度分析:
- 时间复杂度:O(mD2D)O(mD2^D)O(mD2D) ,其中 mmm 为 sss 的长度,即 O(logn)O(\log n)O(logn) ;D=10D=10D=10 。由于每个状态只会计算一次,因此动态规划的时间复杂度 = 状态个数 ×\times× 单个状态的计算时间。本题状态个数为 O(m2D)O(m2^D)O(m2D) ,单个状态的计算时间为 O(D)O(D)O(D) ,因此时间复杂度为 O(mD2D)O(mD2^D)O(mD2D) 。
- 空间复杂度:O(m2D)O(m2^D)O(m2D) 。
相关文章:

LeetCode 1012. Numbers With Repeated Digits【数位DP,数学】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

信息系统项目管理师 第4章 信息系统管理
1.管理方法 1.管理基础 1.层次结构 信息系统是对信息进行采集、处理、存储、管理和检索,形成组织中的信息流动和处理,必要时能向有关人员提供有用信息的系统。 信息系统之上是管理,它监督系统的设计和结构,并监控其整体性能。 …...
:GC如何搞垮线上系统)
JVM系统优化实践(11):GC如何搞垮线上系统
您好,我是湘王,这是我的CSDN博客,欢迎您来,欢迎您再来~看了那么多G1 GC的传说,再来看看怎么预防GC把工程师精心设计的系统给搞垮。在JVM的运行过程中,既有创建对象,又有GC࿰…...

统计软件与数据分析—Lesson2
jupyter Note环境配置,安装及使用以及python数据的读取操作统计软件与数据分析—Lesson21.Jupyter Note环境配置,安装及使用1.1 Jupyter Note 基本操作1.2 Notebook中的Magic开关1.2.1 Magic开关总览1.2.2 Line Magic 全局1.2.3 Cell Magic 当前cell1.3 …...

ISO体系认证全方位解析让!
ISO体系认证全方位解析让! 常常有人问小编, 某某体系是什么意思? 某某证书的有效期是多久? 新版标准的转换要求有哪些? 小编尽量一一解答, 但难免会错过部分朋友的问题。 为了更全面地解决大家关于认证的疑…...

真要被00后职场整顿了?老员工纷纷表示真的干不过.......
最近聊到软件测试的行业内卷,越来越多的转行和大学生进入测试行业。想要获得更好的待遇和机会,不断提升自己的技能栈成了测试老人迫在眉睫的问题。 不论是面试哪个级别的测试工程师,面试官都会问一句“会编程吗?有没有自动化测试…...

NDK FFmpeg音视频播放器二
NDK前期基础知识终于学完了,现在开始进入项目实战学习,通过FFmpeg实现一个简单的音视频播放器。本文主要内容如下:阻塞式队列SafeQueue。音视频BaseChannel基础通道。音视频压缩包加入队列。视频解码与播放。ANativeWindow渲染用到的ffmpeg、…...
Linux之进程信号
目录 一、生活中的信号 背景知识 生活中有没有信号的场景呢? 是不是只有这些场景真正的放在我面前的时候,我才知道怎么做呢? 进程在没有收到信号的时候,进程知道不知道应该如何识别哪一个是信号?以及如何处理它&a…...
AI绘画关键词网站推荐 :轻松获取百万个提示词!完全免费
一、lexica.art 该网站拥有数百万Stable Diffusion案例的文字描述和图片,可以为大家提供足够的创作灵感。 使用上也很简单,只要在搜索框输入简单的关键词或上传图片,就能为你提供大量风格不同的照片。点击照片就能看到完整的AI关键词&#…...

Java-Collections and Lambda
Java SE API know how 集合API 根据算法访选择合适集合 linkedlist不适合搜索 随机访问数据用hashmap 数据保持有序使用treemap 通过索引访问使用数组集合 同步和非同步 访问性能统计 与简单的非同步访问相比,使用任何数据保护技术都会有较小的损失 设置集合…...

KDGX-A光缆故障断点检测仪
一、产品概述 KDGX-A光纤寻障仪是武汉凯迪正大为光纤网络领域施工、测试、维护所设计的一款测试仪表。可实现对光纤链路状态和故障的快速分析,适用于室外维护作业,是现场光纤网络测试与维护中替代OTDR的经济型解决方案。 二、主要特点 1)一键式光纤链路…...
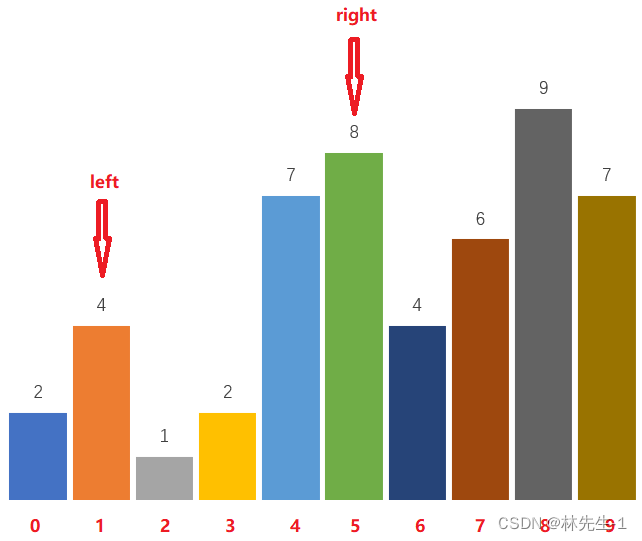
【刷题之路Ⅱ】牛客 NC107 寻找峰值
【刷题之路Ⅱ】牛客 NC107 寻找峰值一、题目描述二、解题1、方法1——直接遍历1.1、思路分析1.2、代码实现2、方法2——投机取巧的求最大值2.1、思路分析2.2、代码实现3、方法3——二分法3.1、思路分析3.2、代码实现一、题目描述 原题连接: NC107 寻找峰值 题目描…...
智能灯泡一Homekit智能家居系列
传统的灯泡是通过手动打开和关闭开关来工作。有时,它们可以通过声控、触控、红外等方式进行控制,或者带有调光开关,让用户调暗或调亮灯光。 智能灯泡内置有芯片和通信模块,可与手机、家庭智能助手、或其他智能硬件进行通信&#…...

外包离职,历时学习416天,成功上岸百度,分享成长过程~
前言: 没有绝对的天才,只有持续不断的付出。对于我们每一个平凡人来说,改变命运只能依靠努力幸运,但如果你不够幸运,那就只能拉高努力的占比。 2020年7月,我有幸成为了百度的一名Java后端开发,…...
利用客户支持建立忠诚度和竞争优势
客户支持可以极大地改变您的业务;最细微、最微妙的差异都会使拥有一次性客户和拥有终身客户之间产生差异。在这篇博文中,我们将揭示客户对企业的忠诚度的三种核心类型,以及如何利用强大的客户支持工具和原则来提高理想的忠诚度并获得决定性的竞争优势。一…...

看他人代码小总结
针对几个功能类似的函数: 1.需要经常调试则定义一个参数比如is_debug来选择是否在调试,定义一些参数专门用于调试用,不用每次都修改这些参数,只需要修改is_debug这个参数; 2.把其中的变量(常量)单独拎出来放到一个文件…...
cudaMemGetInfo()函数cudaDeviceGetAttribute()函数来检查设备上的可用内存
使用CUDA Runtime API中的cudaMemGetInfo()函数来检查设备上的可用内存。该函数将返回当前可用于分配的总设备内存大小和当前可用于分配的最大单个内存块大小。 示例代码,演示了如何在分配内存之前和之后调用cudaMemGetInfo()函数来检查可用内存 size_t free_byte…...

【基础阶段】01中华人民共和国网络安全法
文章目录1 网络安全行业介绍2 什么是黑客和白帽子3 网络安全课程整体介绍4 网络安全的分类5 常见的网站攻击方式6 安全常见术语介绍7 《网络安全法》制定背景和核心内容8 《全国人大常委会关于维护互联网安全的决定》9《中华人民共和国计算机信息系统安全保护条例》10 《中华人…...

隐私计算领域大咖推荐,这些国内外导师值得关注
开放隐私计算 经过近一个月的信息收集,研习社已经整理了多位国内外研究隐私计算的导师资料。邻近考研复试,研习社希望小伙伴们能够通过本文整理的信息,选择自己心仪的老师,在研究生的路途上一帆风顺!1. 国内隐私计算导…...

009 uni-app之vue、vuex
vue.js 视频教程 vue3.js 中文官网 vue.js 视频教程 vue语法:https://uniapp.dcloud.net.cn/tutorial/vue-vuex.html vue2迁移到 vue3:https://uniapp.dcloud.net.cn/tutorial/migration-to-vue3.html Vuex Vuex 是一个专为 Vue.js 应用程序开发的…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
