代码随想录算法训练营day39||动态规划07:多重背包+打家劫舍
多重背包理论
描述:
有N种物品和一个容量为V 的背包。
第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。
求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
本质:
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
——在01背包里面在加一个for循环遍历一个每种商品的数量。
56. 携带矿石资源(第八期模拟笔试)
题目描述
你是一名宇航员,即将前往一个遥远的行星。在这个行星上,有许多不同类型的矿石资源,每种矿石都有不同的重要性和价值。你需要选择哪些矿石带回地球,但你的宇航舱有一定的容量限制。
给定一个宇航舱,最大容量为 C。现在有 N 种不同类型的矿石,每种矿石有一个重量 w[i],一个价值 v[i],以及最多 k[i] 个可用。不同类型的矿石在地球上的市场价值不同。你需要计算如何在不超过宇航舱容量的情况下,最大化你所能获取的总价值。
分析:
先遍历物品,再遍历背包容量,最后遍历物品的个数
——背包遍历:0-1背包+滚动数组,需要逆序遍历;背包容量至少要能装下一个物品,遍历到weight【i】为止
——可放物品个数的遍历:
为什么不放在第二层遍历:会有大量重复,放1、2物品,和放2、3物品是一样的
考虑当前背包是放k个i物品,能装的最大价值是多少?
先考虑k的取值范围:装0个 dp【j】不变,可以不考虑;k要小于物品容量的上
限,同时j要能方向k个物品
注意递推公式:考虑加上k个物品之后的情况!补上k*value
for(int i = 0; i < n; i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量// 以上为01背包,然后加一个遍历个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>int max(int x, int y){return x > y ? x : y;
}int main(){int container,number;scanf("%d%d",&container,&number);int weight[number],prices[number],limit[number];for(int i=0;i<number;i++){//这个写法可以记一下scanf("%d",weight+i);}for(int i=0;i<number;i++){scanf("%d",prices+i);}for(int i=0;i<number;i++){scanf("%d",limit+i);}int dp[container+1];memset(dp,0,sizeof(dp));for (int i=0;i<number;i++){for(int j=container;j>=weight[i];j--){for (int k=1;k<=limit[i] && j-k*weight[i]>=0 ;k++){dp[j]=max(dp[j],dp[j-k*weight[i]]+k*prices[i]);}}}printf("%d\n",dp[container]);return 0;
}总结篇
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
- 动态规划:416.分割等和子集(opens new window)
- 动态规划:1049.最后一块石头的重量 II(opens new window)
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
- 动态规划:474.一和零(opens new window)
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
- 动态规划:322.零钱兑换(opens new window)
- 动态规划:279.完全平方数
198.打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
- 示例 1:
- 输入:[1,2,3,1]
- 输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
- 示例 2:
- 输入:[2,7,9,3,1]
- 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
分析:
实际上j间房屋偷或者不偷有三种情况:
偷了 没偷 j:偷j,是在j-2的基础上+j
没偷 偷了 j:不能偷j,是和j-1是一样的
没偷 没偷 j:如果要偷,同1;如果不偷同2 eg:100,1,1,100
所以本质上是讨论j偷还是不偷的问题,不要去讨论前面各个的状态
确定dp数组(dp table)以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(注意这里是考虑,并不是一定要偷i-1房,这是很多同学容易混淆的点)
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出,递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
确定遍历顺序
dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历!
int rob(int* nums, int numsSize) {int dp[numsSize];//到第i栋房子,最多能偷的钱if(numsSize==0 || numsSize==1) return nums[0];memset(dp,0, sizeof(dp));dp[0]=nums[0];dp[1]=fmax(nums[0], nums[1]);for (int i=2;i<numsSize;i++){dp[i] = fmax(dp[i - 2] + nums[i], dp[i - 1]);}return dp[numsSize-1];
}213.打家劫舍II
力扣题目链接(opens new window)
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,能够偷窃到的最高金额。
示例 1:
-
输入:nums = [2,3,2]
-
输出:3
-
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
-
示例 2:
-
输入:nums = [1,2,3,1]
-
输出:4
-
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
分析:
分成两种情况来解决环的问题!
1、包括环的头结点,不包括尾节点
2、不包括头结点,包括尾节点
再按照打家劫舍1的方法,取两种情况的最大值
即为所求结果
**注意:动态规划是考虑 下标i及下标i 之前的元素,是否能达到某个条件,并不是说一定要选取这个元素的!
**环形问题可以考虑展开
int tryrob(int*nums,int numsSize){if(numsSize==0 || numsSize==1) return nums[0];int dp[numsSize];memset(dp, 0, sizeof(dp));dp[0]=nums[0];dp[1]=fmax(nums[0], nums[1]);for(int j=2;j<numsSize;j++){dp[j]=fmax(dp[j-2]+nums[j], dp[j-1]);}return dp[numsSize-1];
}int rob(int* nums, int numsSize) {if(numsSize==0 || numsSize==1) return nums[0];int a=tryrob(nums, numsSize-1);int b=tryrob(nums+1, numsSize -1);return fmax(a,b);}337.打家劫舍 III
力扣题目链接(opens new window)
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
分析:
暴力递归
对于树的话,首先就要想到遍历方式,前中后序(深度优先搜索)还是层序遍历(广度优先搜索)。
本题一定是要后序遍历,因为通过递归函数的返回值来做下一步计算。——即孩子取值决定了,才能决定父亲的情况
与198.打家劫舍,213.打家劫舍II一样,关键是要讨论当前节点抢还是不抢。
如果抢了当前节点,两个孩子就不能动,如果没抢当前节点,就可以考虑抢左右孩子
动态规划
动态规划其实就是使用状态转移容器来记录状态的变化,这里可以使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
这道题目算是树形dp的入门题目,因为是在树上进行状态转移,我们在讲解二叉树的时候说过递归三部曲,那么下面我以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解。
确定递归函数的参数和返回值
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
所以dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
长度为2的数组怎么标记树中每个节点的状态:在递归的过程中,系统栈会保存每一层递归的参数。
确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回
这也相当于dp数组的初始化
确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
确定单层递归的逻辑
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0]; (如果对下标含义不理解就再回顾一下dp数组的含义)
如果不偷当前节点,那么左右孩子就可以偷
至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
举例推导dp数组
以示例1为例,dp数组状态如下:(注意用后序遍历的方式推导)
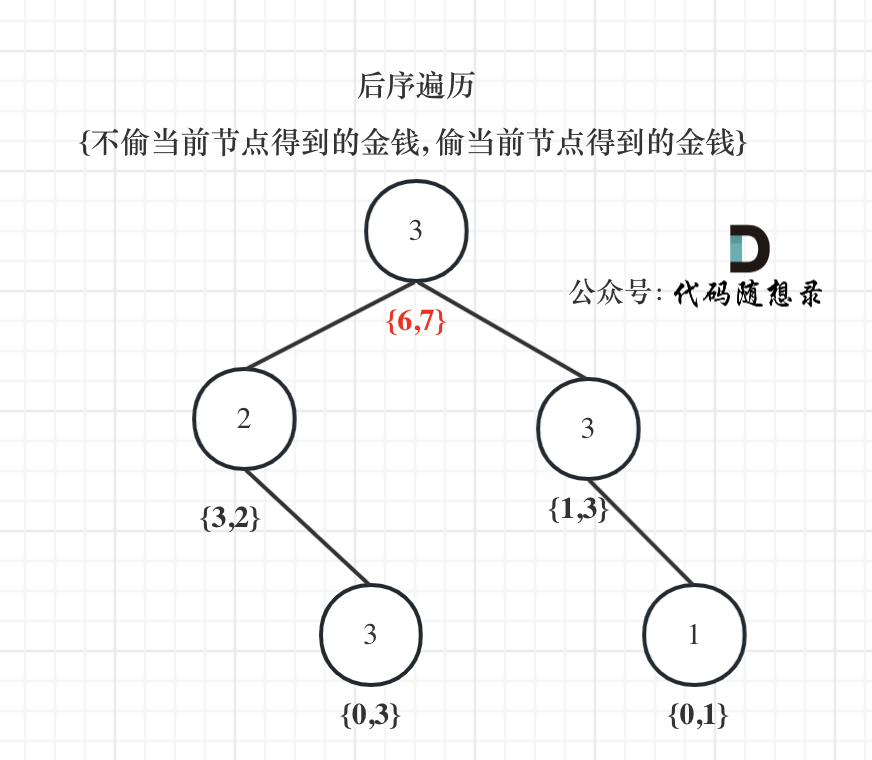
最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱。
int* tryrob(struct TreeNode* root){int* dp=(int*)malloc(sizeof(int)*2);//dp表示在某一个结点往下,0是不抢该结点的最大,1是抢该节点的最大if(root==NULL) {dp[0]=0;dp[1]=0;return dp;}int *left=tryrob(root->left);int *right=tryrob(root->right);//不抢dp的话,也就是dp0,可以抢两个孩子dp[0]=fmax(left[0],left[1])+fmax(right[0],right[1]);//抢dp的话,dp1,两个孩子都不能抢dp[1]=left[0]+right[0]+root->val;return dp;
}int rob(struct TreeNode* root) {int *a=tryrob(root);return fmax(a[0],a[1]);}相关文章:

代码随想录算法训练营day39||动态规划07:多重背包+打家劫舍
多重背包理论 描述: 有N种物品和一个容量为V 的背包。 第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。 求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。 本质: …...

WebSocket革新:用PHP实现实时Web通信
标题:WebSocket革新:用PHP实现实时Web通信 在现代Web应用中,实时通信是一个不可或缺的功能。WebSocket作为一种在单个TCP连接上进行全双工通信的协议,它允许服务器主动向客户端推送数据,极大地简化了客户端和服务器之…...

Python教程(十三):常用内置模块详解
目录 专栏列表1. os 模块2. sys 模块3. re 模块4. json 模块5. datetime 模块6. math 模块7. random 模块8. collections 模块9. itertools 模块10. threading 模块11. 加密 模块 总结 专栏列表 Python教程(十):面向对象编程(OOP…...

Linux 下的进程状态
文章目录 一、运行状态运行队列运行状态和运行队列 二、睡眠状态S状态D状态D状态产生的原因 三、暂停状态T状态t 状态 四、僵尸状态为什么有僵尸状态孤儿进程 一、运行状态 R状态:进程已经准备好随时被调度了。 运行队列 每个 CPU 都会维护一个自己的运行队列&am…...

【设计模式】六大基本原则
文章目录 开闭原则里氏替换原则依赖倒置原则单一职责原则接口隔离原则迪米特原则总结 开闭原则 核心就一句话:对扩展开放,对修改关闭。 针对的目标可以是语言层面的类、接口、方法,也可以是系统层面的功能、模块。当需求有变化的时候&#…...

Selenium网页的滚动
网页滚动功能实现 网页的滚动 如果需要对网页进行滑动操作,可以借助浏览器对象调用execute_script()方法来执行js语句,从而实现网页中的滚动下滑操作。 使用js语法实现网页滚动: # 根据x轴和y轴的值来定向滚动对应数值的距离 window.scrol…...

图算法系列1: 图算法的分类有哪些?(上)
大约在公元9世纪上半叶,来自中亚古国花剌子模的波斯数学家花剌子米(al-Khwarizmi)先后出版了两本对数学界有深远影响的书籍《印度数字算术》与《代数学》,前者在12世纪被翻译为拉丁文传入欧洲,十进制也因此传入欧洲,最终所形成的…...
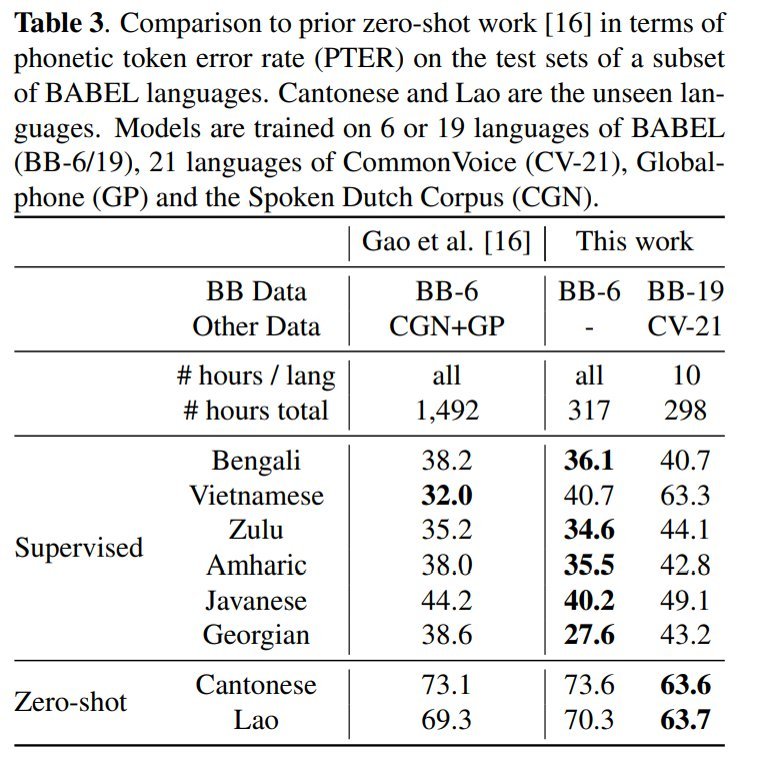
零样本学习——从多语言语料库数据中对未学习语言进行语音识别的创新技术
引言 在全球众多的语言中,只有极少数的语言在语音识别领域取得了显著的进展。这种不平衡现象的主要原因是,现有的语音识别模型往往依赖于大量的标注语音数据,而这些数据对于许多语言来说难以获得。 近年来,尽管语音识别技术取得…...

ViewStub的原理
**ViewStub是Android开发中的一个轻量级控件,主要用于懒加载布局以提高应用程序的性能和响应速度。**其原理和工作方式如下: 定义与特点 轻量级与不可见:ViewStub是一个不可见的、不占布局位置的轻量级View,它在初始化时不会实例…...

十一、Spring AOP
十一、Spring AOP 1. AOP概述2. Spring AOP快速⼊⻔2.1 引⼊AOP依赖2.2 编写AOP程序 3. Spring AOP 详解3.1 Spring AOP核⼼概念3.1.1 切点(Pointcut) Around 哪个包3.1.2 连接点(Join Point) 包下面的方法3.1.3 通知(Advice) 就是要执行的方法3.1.4 切⾯(Aspect) 3.2 通知类型…...
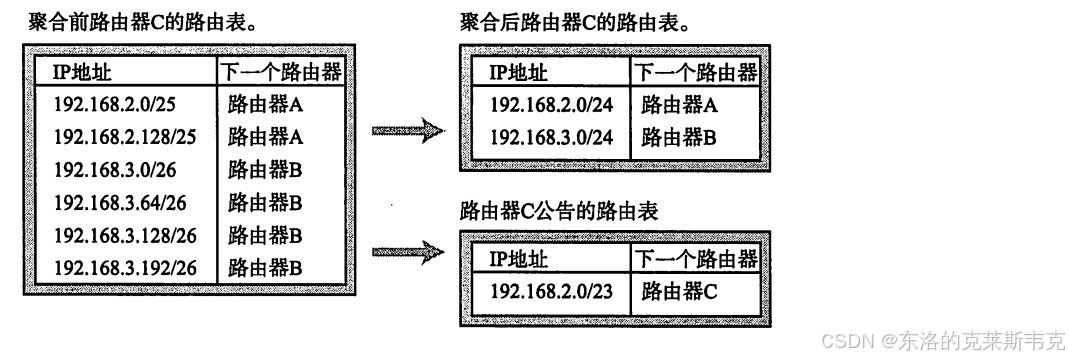
【网络】IP的路径选择——路由控制
目录 路由控制表 默认路由 主机路由 本地环回地址 路由控制表的聚合 网络分层 个人主页:东洛的克莱斯韦克-CSDN博客 路由控制表 在数据通信中,IP地址作为网络层的标识,用于指定数据包的目标位置。然而,仅有IP地址并不足以确…...
Unity动画模块 之 2D IK(反向动力学)
本文仅作笔记学习和分享,不用做任何商业用途 本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 1.什么是IK 反向动力学 IK(Inverse Kinematics)是一种方法,可以根据某些子关节的最…...
关于kickstart自动安装脚本以及dhcp的设置
我将在rhel7.9内进行本次实验,需要安装并启动图形界面 hostnamectl查看是否有图形界面 没有的话 可以使用yum group list 查看,并安装server with GUI yum group install "server with GUI" -y安装完成后可以使用init 5启动 安装kickstart自…...

AWS云服务器选择最佳区域
2024年,随着全球云计算的持续发展和AWS在全球不断扩展的数据中心网络,选择合适的AWS云服务器区域成为了企业和开发者需要认真考虑的问题。九河云告诉你在做出选择之前,需要考虑以哪些关键因素: 地理位置和用户分布 选择AWS云服务…...

Unity Android端截图保存并获取展示
截屏保存方法 public static IEnumerator ScreenShot(string filePath, string fileName){yield return new WaitForEndOfFrame();Rect rect new Rect(0, 0, Screen.width, Screen.height);Texture2D screenShot new Texture2D(Screen.width, Screen.height, TextureFormat.R…...

linux高级编程——文件IO
linux高级编程——文件IO 标准IO:stdio.h 标准IO:stdio.h IO也就是输入input和输出output; I: 键盘是标准输入设备,默认输入就是指键盘 /dev/input; O: 显示器是标准输出设备,默认输…...
)
windows C++-在 C++/WinRT 中使用委托处理事件(下)
撤销已注册的委托 当你注册委托时,通常会向你返回一个令牌。 随后,可以使用该令牌撤销委托;这意味着将从事件取消注册委托,再次引发该事件时不会调用该委托。 为简单起见,上面的代码示例都没有介绍如何执行该操作。 …...

【实用工具】Stirling-PDF: 优质开源的PDF处理工具/编辑工具-含入门安装教程
文章目录 项目简介功能展示Page Operations 页面操作Conversion Operations 转换操作Security & Permissions 安全与权限Other Operations 其他业务 如何安装并使用Docker RunDocker Compose 项目简介 这是一款使用 Docker 的基于本地托管网络的强大 PDF 操作工具。它能让…...

opencv 深度图视差图可视化案例
参考:https://www.cnblogs.com/zyly/p/9373991.html(图片这里面下载的) https://blog.csdn.net/He3he3he/article/details/101053457 原理 双目摄像头 视差公式: 三角形对应推算 深度距离转换: 这里d是视差Disparity 代码 下面两种计算视差方法: import os impor…...

Golang | Leetcode Golang题解之第330题按要求补齐数组
题目: 题解: func minPatches(nums []int, n int) (patches int) {for i, x : 0, 1; x < n; {if i < len(nums) && nums[i] < x {x nums[i]i} else {x * 2patches}}return }...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...
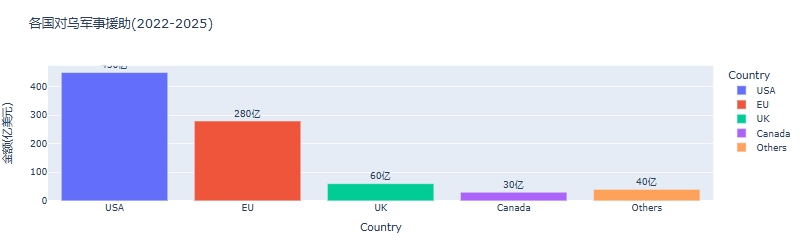
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...

DriveGPT4: Interpretable End-to-end Autonomous Driving via Large Language Model
一、研究背景与创新点 (一)现有方法的局限性 当前智驾系统面临两大核心挑战:一是长尾问题,即系统在遇到新场景时可能失效,例如突发交通状况或非常规道路环境;二是可解释性问题,传统方法无法解释智驾系统的决策过程,用户难以理解车辆行为的依据。传统语言模型(如 BERT…...
